利用改进型Lennard-Jones 势能函数状态方程对聚乙二醇物质密度性质的研究★

何思源，卢银彬

（1.贵州水利水电职业技术学院，贵州 贵阳 550000；2.西安石油大学机械工程学院，陕西 西安 710065）

聚乙二醇类物质一直以来在化工领域应用中被视为有前景的有机溶剂而被广泛应用与研究。聚乙二醇对矿物盐等诸多物质具有良好的溶解性，可作为金属-有机材料、特别是一锅法合成反应中的媒介溶剂而使用。化工领域内工艺的开发与优化设计通常依赖工程建模予以实现，该过程需要工质在相应条件下准确的热物理性质数据，尽管聚乙二醇类物质在各行业里取得广泛的应用，但它们热物理性质的实验及理论研究工作还相对有限，因此对这些工质相关性质展开研究尤显必要。

流体密度在过程计算与仿真、设备与系统管道设计、液体计量计算等实际工程问题中是不可缺少的物性参数之一，除实验测量方法以外，也经常通过拟合方法或状态方程予以计算得到。在过去几十年里，国内外学者对流体密度的理论研究开展了大量工作，早期的立方型状态方程如SRK[1]和PR[2]方程因其方程型式简单、易于理解和掌握，在石油化工领域里应用广泛；学者Lempe[3]与Abudour[4]分别建立了比容平移法修正的SRK 和PR 状态方程，用于对饱和液体密度的关联与计算；文献中[5-6]也报道了链扰动统计缔合流体理论方程（PC-SAFT 方程）对碳氢化合物、离子液体密度的理论研究工作；Baled 等研究人员[7]建立的体积修正PR 方程和SRK 方程模型，对从C-1～C-40 的正构烷烃类流体在0.1 MPa 至276 MPa的压力范围的密度展开关联计算；近几年来，改进型Lennard-Jones 势能函数状态方程被先后应用于制冷剂、烷烃类、离子液体的密度预测[8-10]，因此，将该模型推广用于其他工质密度的研究在工程领域中的应用具有显著意义。

1 改进型Lennard-Jones 密度理论方程

线性等温线规则密度方程（LIR 方程）是基于Lennard-Jones 势能函数平均有效对势能理论，并结合成对加法近似模型推导建立的理论方程，该方程表达式[11]为式（1）：

式中：a（T）=（a2-a1）/RT，b（T）=b1/RT，其中a1和b1分别为平均有效对势能函数的引力项和斥力项，a2为非理想热压。

LIR 方程对非极性、极性和量子流体在高于波义尔密度（ρB=1.8ρC）和低于2 倍波义尔温度[TB=（2.5～2.7）TC]的区间范围内计算精度良好。为了进一步提高该理论在多类型溶液和较大范围温度压力区间的预测效果，学者Ghateee 和Bahadori[12]基于Mie 有效势能模型提出的状态方程对液态铯和其他液态金属流体的密度进行研究，其表达式如式（2）所示：

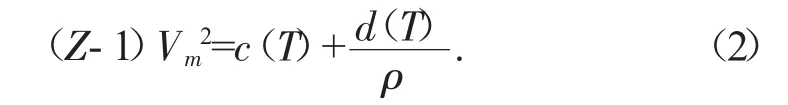
其中：c（T）=（c2+c1）/RT，d（T）=d1/RT，c1与d1分别为平均有效对势能函数的引力项和斥力项，c2为振动能量效应参数。

尽管方程式（1）和式（2）可分别适用于对低分子流体或金属液体密度的计算，但它们仍然存在许多工质和相应的温度压力条件无法满足计算精度的情况，因两者的局限性，Parsafar 等学者[13]在考虑流体分子有效相邻对作用因素的基础上，结合Lennard-Jones函数建立了改进型Lennard-Jones 势能函数状态方程（ELJ 方程）式（3）：

式中：e（T）、f（T）与g（T）均为温度相关系数，其表达式分别为式（4）～式（6）：

式中：ei，fi与gi均为与温度无关的常量参数，它们的具体数值与不同的流体种类相对应；利用流体在相应压力范围内的密度实验数据可以回归得到状态方程中e（T），f（T）和g（T）在各温度下的参数值，再通过方程式（4）～式（6）进行拟合可以得到ei，fi与gi，根据实验数据回归得到的上述参数，再结合ELJ 方程即可计算出流体在不同压力、温度条件下的密度值[见式（7）]：

2 计算结果分析

本文从文献[14-15]中收集了乙二醇、丙二醇、二甘醇、三甘醇、四甘醇、五甘醇、六甘醇与聚乙二醇400 共8 种聚乙二醇类物质在0.1 MPa～350 MPa、273 K～363 K 的压力温度区间内的密度实验数据，基于ELJ状态方程的理论框架回归得到各物质所对应的状态方程系数;方程（3）中的温度系数e（T）、f（T）和g（T）根据等温线上不同压力的密度实验数据回归得到，所研究流体分别对应的方程温度系数见表1 所示，为了能够应用该状态方程计算不同温度下的流体密度，在此根据方程式（4）～式（6）对不同温度下的方程温度系数进行拟合，从而得到与温度压力无关的状态方程常量参数e0～e3，f0～f3，g0～g3，各物质所对应的状态方程常量参数回归结果见表2。

表1 本文所回归的ELJ 状态方程温度系数e（T）、f（T）和g（T）结果以及对研究物质密度计算的结果[14]

表2 本文研究各物质对应的ELJ 状态方程常量参数e0～e3，f0～f3，g0～g3 回归结果

2.1 ELJ 状态方程预测值与实验值的对比

本文在ELJ 状态方程的基础上，利用实验数据回归得到的状态方程常量参数对聚乙二醇流体密度展开研究，密度计算值与实验值的绝对平均偏差结果列于表1 所示，利用ELJ 状态方程与所回归方程参数对所研究聚乙二醇物质密度计算的绝对平均偏差在0.09%以内，在图1～图4 中分别给出了四甘醇、五甘醇、六甘醇、聚乙二醇400 在高温高压条件下密度实验值与状态方程预测值的比较情况，对所研究流体密度取得良好的关联结果。

图1 ELJ 状态方程对四甘醇在283 K～363 K、0.1 MPa～95 MPa 温度压力区间内密度的预测结果

图2 ELJ 状态方程对五甘醇在283 K～363 K，0.1 MPa～95 MPa 温度压力区间内密度的预测结果

图3 ELJ 状态方程对六甘醇在283 K～363 K，0.1 MPa～95 MPa 温度压力区间内密度的预测结果

图4 ELJ 状态方程对聚乙二醇400 在283 K～363 K，0.1 MPa～95 MPa 温度压力区间内密度的预测结果

2.2 ELJ 状态方程与其他方程对密度计算结果的对比

为了验证ELJ 状态方程的优越性，本文将该模型与其他状态方程，如SRK[1]、PR[2]、比容平移法修正的VT-SRK 和VT-PR 方程[3-4]对密度的计算结果进行了比较；各方程对本文所研究聚乙二醇类物质密度计算的绝对平均偏差结果总结列于表3 所示；研究结果表明，ELJ 状态方程相较于其他方程对流体密度在高温高压条件下计算的精度有显著提高。

表3 ELJ 状态方程与其他状态方程对对研究物质密度计算结果的对比

3 结语

本文基于改进型Lennard-Jones 势能函数状态方程对乙二醇、丙二醇、二甘醇、三甘醇、四甘醇、五甘醇、六甘醇与聚乙二醇400 共8 种聚乙二醇类流体在0.1 MPa～350 MPa，273 K～363 K 压力温度范围内的密度性质展开研究，根据文献报道的684 个PVT 实验数据回归得到各工质所对应的状态方程常量参数，对该模型在不同种类物质密度的研究和应用领域进行了拓展。研究结果显示，该方程对所研究流体密度计算的绝对平均偏差为0.085%，在高温高压条件对聚乙二醇类流体密度取得良好的预测效果，在计算精度上可以满足研究物质在工程应用中的需求。

ELJ 状态方程对流体密度的预测同样提供了一种简便的计算方法，与以往时期文献中报道的诸如PR、SRK 等立方型状态方程相对比，本文所研究的状态方程模型并不需要流体的临界参数Pc、Tc 作为输入参数对密度来进行计算，因此，该模型对仍然缺少临界参数数据的工质密度的理论研究工作具有显著的意义；此外，本文通过对ELJ 方程与PR、SRK 以及体积平移修正的PR,SRK 方程对聚乙二醇类物质的密度分别予以研究，计算结果表明ELJ 方程对研究物质流体密度的预测效果相较于其他状态方程具有较高的优越性。

符号说明

Z——压缩因子；

ρ——流体密度，kg·m-3；

Vm——流体摩尔体积，m3·mol-1；

T——热力学温度，K；

p——压强，MPa；

R——理想气体常数，8.314 5 J·mol-1·K-1；

e（T），f（T），g（T）——ELJ 状态方程温度相关系数；

ei，fi，gi——ELJ 状态方程常量参数