基于改进CFCC 特征提取的语种识别算法研究

龙华，黄张衡，邵玉斌，杜庆治，苏树盟

（昆明理工大学信息工程与自动化学院，云南 昆明 650500）

0 引言

语种识别（LID,language identification）作为语音信号处理的前端系统，根据语音序列所表征的不同特征信息识别出所属的语言类别，广泛应用于语种识别系统、智能系统等[1]。传统的语种识别系统通常基于不同语音所具有的音素层特征与声学层特征，音素层特征采用了每个语种之间的音节和音素的出现频率与组合方式的差异作为分类依据来进行语种识别[2]。声学特征则通过对语音信号进行一系列的变换提取出能够表征整个语音信号的局部特征来进行分类识别。随着科技的进步以及研究者之间的密切联系合作，对语种识别技术的精确度要求也越来越高，特别是在噪声环境下能够有效提取具有稳定性与稳健性的声学特征尤为关键。

常用的声学特征包括基于梅尔滤波器的梅尔频率倒谱系数（MFCC,Melfrequency cepstral coefficient）[3-4]、伽玛通频率倒谱系数[5]（GFCC,Gammatone frequency cepstral coefficient）以及耳蜗滤波器倒谱系数[6]（CFCC,cochlear filter cepstral coefficient）。文献[7]首次提出使用小波变换作为耳蜗滤波器的冲激响应函数来模拟人耳听觉过程提取传统CFCC 特征并应用于语音识别，取得了一定的识别效果。但由于小波变换主要在时域对信号进行分析，在分数域并不能很好地对信号进行有效处理，且在低信噪比下传统CFCC 的抗噪性能并不理想[8]。

为了提升CFCC 在低信噪比下的抗噪稳健性，李晶皎等[9]利用信号相位匹配方法消除语音信号噪声，再将Teager 能量算子融合CFCC 特征组成新的特征参数，相较单一特征，融合特征提升了语种识别准确率。文献[10]将语音相位特征与CFCC 特征相融合应用于说话人识别系统来提高系统的识别准确率和稳健性。虽然融合特征的识别准确率以及抗噪性有所提升，但是其仅单纯地进行特征融合，语音信号时域信息的固有不足以及信号时频域、分数域信息未能被有效地表征[11]，需要考虑信号的时频域以及分数域信息。Patel 等[11]提出基于对数非线性函数和瞬时频率来提取CFCC 特征参数进行语音信号的检测，其提取的特征具有较高的抗噪性，且弥补了传统CFCC 特征不能有效提取信号中时频域信息的缺陷，但其未能有效分析信号分数域中的信息[8]。为了进一步提升低信噪比下语音识别性能，文献[12]在特征提取前端引入语音增强技术，通过谱减法与特征提取相融合，提取更具稳健性的特征。其在特征提取前端进行降噪处理，在特征提取的过程中进行了非线性信号压缩，但也忽略了特征中的分数域信息。

上述方法提取CFCC 特征参数并未有效考虑噪声环境下语音信号的时频域、分数域信号信息以及语音信号中所含有的声压强度对特征参数的影响。本文首先在特征提取前端引入自适应滤波[13]对语音信号进行增强处理。然后采用新型分数阶小波变换代替小波变换作为小波基函数来模拟信号在耳蜗基底膜上的传播过程，以弥补小波变换不能有效在分数域表征特征的缺陷，且能够在时频域以及分数域对信号进行多辨分析。另外，基于小波变换以及分数阶小波变换的耳蜗滤波函数都未能表现出基底膜滤波器的非对称性与声压强度[14]，因此，在分数阶小波变换滤波函数中引入能够反映声音强度的啁啾参数[15]以更有效地反映语音信号在耳蜗中的声压强度，使提取到的特征更具区分性。再利用非线性幂函数对信号进行压缩处理，将其由能量值变为感知响度，得到基于自适应滤波的新型分数阶耳蜗滤波器倒谱特征（NFCFCCAF,new fractional cochlear filter cepstral coefficient based on adaptive filtering）。该特征突破了传统CFCC 特征基于小波变换与立方根线性函数局限于时频域分析信号的缺点，在能够继承多分辨分析优点的同时还可以对噪声信号在时频域和分数域进行多辨分析[14]。最后，将提取到的特征语谱图输入分类网络FcaNet-MobileNetV2 中进行分类识别。

1 CFCC 提取

CFCC 是基于听觉感知模拟人耳的听觉过程提取的，传统的CFCC 特征采用听觉正变换模拟声音从外界传入人耳经过鼓膜放大声波振动能量，再通过镫骨底板的活塞运动传入内耳耳蜗引起耳蜗基底膜上的振动。文献[6]采用小波基函数作为耳蜗滤波函数通过小波变换来模拟信号在耳蜗基底膜上的运动，使信号通过耳蜗滤波器组、毛细胞窗口、非线性响度变换以及离散余弦变换（DCT,discrete cosine transform）来实现CFCC 特征提取。

小波变换能够突破时频域的局限，更好地处理分析非线性信号，设原始时域语音信号x(t)，经听觉变换输出T(a,b) 定义为

其中，耳蜗基底膜上的冲击响应函数ψa,b(t)定义为

其中，α＞ 0,β＞ 0，α和β决定了ψa,b(t)的时频域形状和宽度，一般情况下，α=3 且β=0.2 时降噪效果较佳。a为尺度因子，0＜a≤1，由耳蜗滤波器组的最低中心频率fL与中心频率fC的比值决定，即；b为位移因子，为随时间可变的实数；θ为控制冲激响应角度的初始相位；u(t) 为单位阶跃函数，是单位冲激函数的积分。

毛细胞函数用来模拟人耳耳蜗基底膜上由大量毛细胞构成的螺旋器（柯蒂氏器），通过螺旋器毛细胞的换能作用把声波的机械振动能量转变为生物电能最终转化为大脑可分析的电信号。其模拟过程为

当前滤波器中心频率响应相关神经穗就可以用每个波段的毛细胞输出S(i,j) 来表示，即

最后，将非线性响度变换输出经DCT 进行去相关得到传统CFCC。

2 改进特征提取

2.1 基于VMD 的自适应滤波降噪

本节主要研究低信噪比环境下的语种识别，定义采样后带噪声的语音信号为

其中，x(n)为原时域语音信号x(t)采样后的信号，g(n) 为零均值高斯白噪声，其平均信噪比定义为

为了进一步提高带噪语音信号的识别性能，可以在特征提取前端对语音信号进行滤噪处理。由于本文实验采用添加零均值高斯白噪声后的语音信号，高斯白噪声属于平稳噪声，而常用的频域滤波法可以对带噪信号进行处理，但对于带内噪声其降噪效果并不佳[13]。对于平稳噪声，自适应滤波却能够不完全依赖噪声信号的先验统计特性而根据算法自适应调整参数，使输出信号达到最优，且对带内噪声有更好的处理效果[16-17]。本文实验对带噪语音信号进行变模态分解（VMD,variational mode decomposition）处理，然后通过基于归一化最小均方（NLMS,normalization least mean square）自适应滤波器降噪，该方法对平稳噪声有较好的处理效果。基于VMD 的自适应滤波系统如图1 所示，其中，s(n) 为带噪语音信号，y(n) 为自适应滤波器的输出，W为滤波器的权值系数向量，e(n) 为误差信号，对输入带噪语音信号进行端点检测后，取出语音信号中的所有无话帧并求取均值作为信号的参考噪声n(n)，因此参考信号为

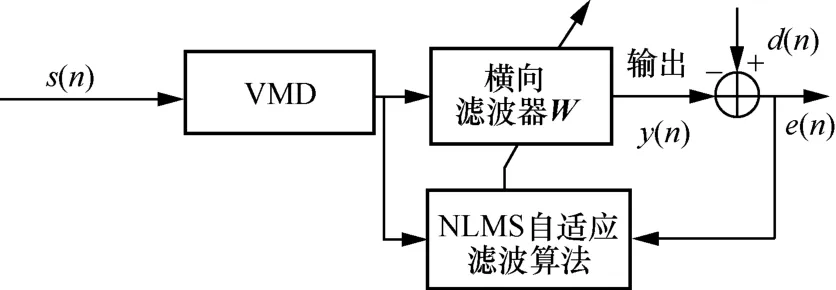
图1 基于VMD 的自适应滤波系统

当均方误差达最小时，滤波器的系数向量为最佳权值，滤波器的滤波效果最佳。对于M阶滤波器，输出y(n) 可表示为

其中，wm(n)为权值系数，则自适应滤波的权值系数向量为

滤波器的输入信号向量为

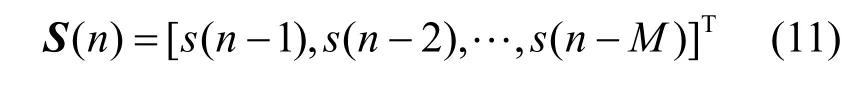
则输出信号为

误差信号e(n) 可表示为

则误差平方的数学期望为

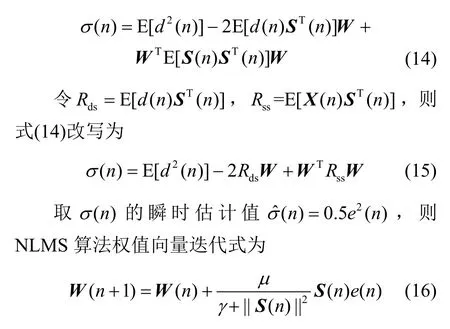
其中，μ为收敛系数，主要控制算法的收敛速度与稳定误差；γ取0.001。

为了测试自适应滤波法在低信噪比下的降噪效果，设计实验在 -10～0 dB 噪声下对带噪语音信号进行降噪处理。本文实验引入占空比来描述自适应滤波的降噪效果，占空比定义为一段带噪语音信号中纯噪声时间与语音信号时间的比值，主要反映了纯噪声时间的长短对自适应滤波降噪的影响。首先采用 -10～0 dB 信噪比的带噪语音信号各1 000 条，在每一信噪比下分别对带噪语音信号进行端点检测，求出其占空比，实验发现语音信号的占空比在20%～40%之间。因此将每一信噪比下语音信号以5%占空比为刻度分为5 类，并对每一类占空比下语音信号进行降噪滤波后求取改善信噪比均值。其在不同信噪比、不同占空比下的改善信噪比和均方根误差分别如图2 和图3 所示。

图2 不同信噪比、不同占空比下的改善信噪比

图3 不同信噪比、不同占空比下的均方根误差

从图2 和图3 中可以看出，自适应滤波在低信噪比下对不同占空比的带噪语音信号降噪效果相对稳定，当占空比为30%时，其滤噪后改善信噪比较其他占空比要高，且整体相对稳定。

在信噪比为-5 dB、不同占空比下自适应降噪过程中的收敛情况如图4 所示，分析不同占空比下前10 000 个采样点、100 次重复实验时的平均均方根误差。从图4 中可以看出，随着迭代次数的增加，不同占空比下的曲线很快便收敛，其中当占空比为20%时，收敛速度最快，在迭代2 000 次时便收敛，其滤噪效果较佳。在不同信噪比、不同占空比下的实验结果表明，采用自适应滤波降噪在不同占空比下均有较快的收敛速度，且降噪效果比较稳定。

图4 不同占空比下收敛曲线

2.2 基于新型分数阶小波变换的NFCFCCAF 特征提取

传统的小波变换虽然能够突破时频域限制对噪声信号进行有效处理，但小波变换主要是基于时频域信号，不具有分数傅里叶变换分数域表征的缺陷[18]，其在分数域中并不能有效表征信号局部特征。而分数阶小波变换不仅可以在时频域与分数域分析信号，而且在继承多分辨分析优点的同时还可以对信号在时频域与分数域进行多辨分析，更具抗噪性。

设带噪语音信号s(n)经自适应滤波降噪后的连续语音信号为s(t)，采用分数阶母小波函数ψp,a,b(t)作为耳蜗基底膜上的耳蜗滤波函数，则语音信号经听觉变换输出FRWT(p,a,b)为

设时间函数为h(t)，在分数傅里叶变换下，分数阶卷积定义为

其中，Θp为分数阶卷积算子，S p(u)与H(ucscω)分别为s(t)与h(t)的p阶分数傅里叶形式。则分数阶小波变换分数域形式表示为

其中，ψ*(aucscω)为ψ(t)的FT（变换元进行了尺度cscω伸缩），核函数Γp(u,b)定义为

其中，u为分数频率。因此，式(17)可以改写为

由于特征提取中耳蜗滤波函数的幅频响应曲线关于中心频率对称，其并未有效体现人耳基底膜曲线的非对称性，且其幅频响应曲线也与强度无关，这与基底膜的强度相关特性并不相符[15]。因此，为了更有效地体现出人耳基底膜曲线的非对称性且符合人耳基底膜的强度相关特性，使函数能够对语音信号进行有效处理，在耳蜗滤波器函数中引入一个能够反映声音强度的啁啾参数为对时间的对数，啁啾因子ξ随着声压强度sP（单位为dB）的变化而变化[15]。

其中，P0=2×10-5Pa 为参考声压，Pe为有效声压。

其中，N为所取的采样点数，xn为对语音信号x(t)的采样点。语音信号的声压级曲线如图5 所示。

图5 语音信号的声压级曲线

声压作为声扰动而产生的逾量压强，是空间位置和时间的函数，可以定量描述声波，声压强度级能够随着声音的不同而变化，更好地反映了人耳对声音强弱的变化。因此，在耳蜗滤波函数中加入反映声压强度的啁啾参数的新型耳蜗滤波器函数定义为

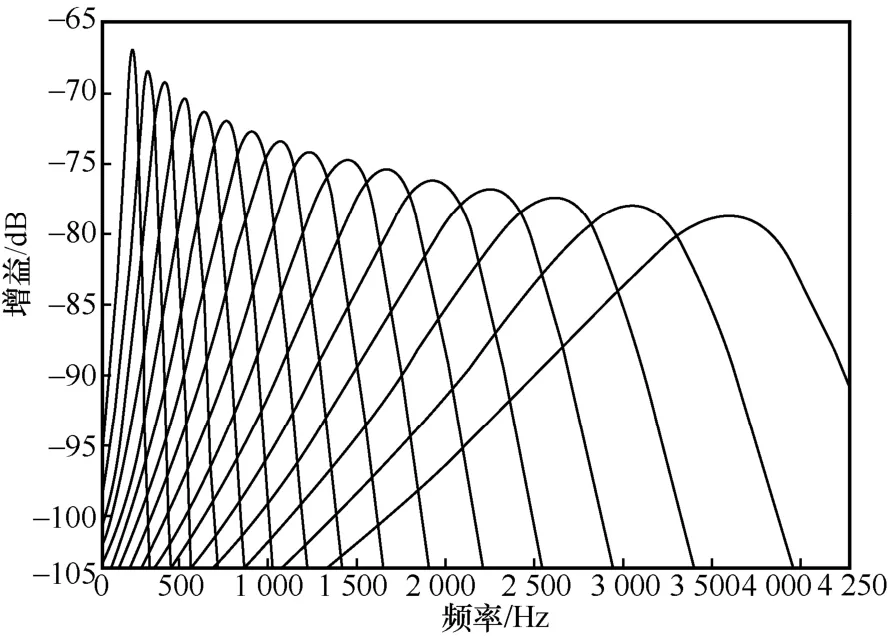
图6 新型耳蜗滤波器组函数的频率响应

则语音信号经听觉变换输出NFRWT(p,a,b)由式(22)改为

毛细胞滑动窗口函数定义为

传统CFCC 特征提取过程中响度函数采用式(5)立方根形式，其可以有效地模拟信号，还可以为非线性幂函数或对数形式。通过实验对比可知，在噪声环境下立方根函数与对数函数较非线性幂函数的识别效果并不理想[12]，因此本文实验采用非线性幂函数来模拟人耳听觉特性。由于非线性幂函数更符合人耳听觉神经的压缩感知，通过非线性幂函数来对毛细胞输出信号进行非线性响度变换，使其由能量值变为感知响度[12]。实验中通过对比调整不同幂函数，当幂函数的指数取0.25 时识别性能最佳，因此，实验中模拟过程为

将非线性响度变换输出经离散余弦变换进行去相关，即

其中，n为特征变换后每帧特征的维数，M为耳蜗滤波器个数，0＜n＜N,0 ≤m≤M。

由于人耳在不同频率声波之间的听觉敏感度存在差异，频率较低的声音在人耳的耳蜗基底膜上行波传递的距离远大于频率较高的声音。因此，通过升半正弦倒谱提升来减少低维中分量的占比，进而可提升高维分量的作用，升半正弦倒谱窗函数定义为

倒谱提升后的CFCC 为

最后得到新的特征参数NFCFCCAF，其提取过程如图7 所示。

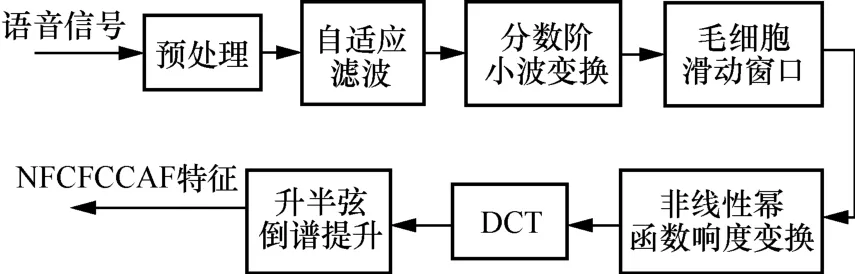
图7 NFCFCCAF 提取过程

2.3 动态特征提取

采用新型分数阶小波基函数作为耳蜗基底膜上的耳蜗滤波函数，模拟人耳听觉过程提取的特征参数反映了语音信号的静态特性，而人耳听觉过程具有动态特性，为了更好地模拟听觉过程，本文实验提取了能够表征语言信号动态特性的一阶差分ΔNFCFCCAF 特征，再将其与NFCFCCAF 特征进行融合构成融合特征NFCFCCAF-DS，以提升语种识别准确率。最后将融合特征与NFCFCCAF 特征作为不同分类网络的输入进行语种识别比较，以验证本文算法提取特征的稳健性与有效性。

3 FcaNet-MobileNetV2 识别模型

目前，ResNet 广泛应用于语种识别且能够表现出高竞争力的识别性能，但其在小样本数据集中网络的宽度和深度容易出现过拟合现象，降低整个网络的泛化能力[19]。因此实验采用基于倒残差结构的MobileNetV2网络来进行准确率测试，以对小样本数据集进行有效处理，提取特征中更多的高维信息[20]。且所提取NFCFCCAF 特征中包含了大量的频域信息[8]，因此通过在网络模型中引入频域注意力机制使网络模型能够捕捉更多的频域信息，提升网络的区分性。

本文将轻量化卷积神经网络MobileNetV2[20]作为识别模型的主干网络，在其17 个瓶颈结构中添加了注意力机制模块FcaNet[21]构成FcaNet-Mobile-NetV2 分类识别模型。其中，FcaNet 作为频域通道注意力机制，是对SENet[22]的改进，由于SENet 的全局平均池化（GAP,global average pooling）为二维离散余弦变换的低频部分，而特征图中大量的中高频信息被舍弃了。因此，文献[21]提出了多谱注意力模块FcaNet，将通道注意力机制的压缩扩展到了频域，进而引入更多的频率分量信息以达到识别度提升的目的。MobileNetV2 属于轻量级识别网络，其是在MobileNetV1 网络的基础上改进反向残差块与线性瓶颈而来的，在保留了MobileNetV1 网络中深度可分离卷积加速网络思想的同时能够更好地提取关键信息提升识别准确率[23]。因此，为了更好地提取出特征语谱图中的关键频域信息且有效地分类识别，本文在MobileNetV2 主干网络瓶颈中加入频域通道注意力机制模块以辅助其有效地提取特征语谱图中的特征信息，组成FcaNet-MobileNetV2 识别模型，如图8 所示。

图8 FcaNet-MobileNetV2 识别模型

4 实验结果及分析

4.1 数据准备及参数设置

1) 数据准备

本文实验采用公共数据集语料库LibriVox 中的单通道wav 音频信号文件，其中包括英语、法语、德语、意大利语、西班牙语这5 个语种。语音的采样率fs=16 000 Hz，每条语音信号时长为3 s，总共有10 000 条实验语音，每个语种分别有1 400 条训练集与600条测试集语音文件。实验以NoiseX-92[24]公共噪声库中的白噪声为噪声源，构建了信噪比分别为 5-dB、0 dB、5 dB、10 dB、15 dB 情况下的训练测试语料并且在每个数据集所对应的语种分别打上标签，如表1 和表2 所示。

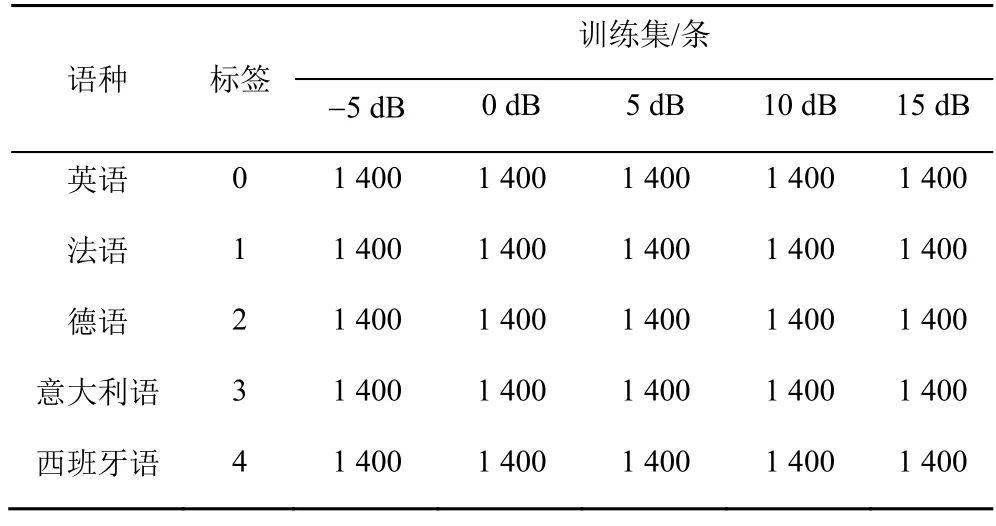
表1 不同语种实验训练集

表2 不同语种实验测试集

本文实验采用融合了频域通道注意力机制的轻量化卷积神经网络FcaNet-MobileNetV2 作为分类网络对特征语谱图进行分类识别。其中，分类网络的训练圈数epoch 参数设置为50，batchsize 为50，worker数为4，模型的学习率设置为0.000 1；将提取出的二维特征输入分类网络中训练10 次，将每次神经网络最后一次循环的输出节点作为语种的识别模型来对语种测试集进行识别，取10 次结果的平均值作为语种识别结果。性能评价指标采用美国国家标准与技术研究院语种评测规则，表示为

其中，EL为英语的正确识别个数，FL为法语的正确识别个数，GL为德语的正确识别个数，IL为意大利语的正确识别个数，SL为西班牙语的正确识别个数，TL为测试集总数，为语种识别准确率。

4.2 实验

1) 实验1

为了验证本文提出的非线性幂函数对信号进行压缩模拟过程提取的耳蜗滤波器倒谱系数（FCFCC,function of cochlear filter cepstral coefficient）与基于立方根函数、非线性函数提取的CFCC的语种识别效果，实验提取了传统CFCC 特征，采用本文所提非线性幂函数式(32)提取的FCFCC 特征，文献[11]中基于对数非线性函数的耳蜗滤波器倒谱系数（LCFCC,logarithm of cochlear filter cepstral coefficient）以及文献[12]、文献[25]所提基于非线性幂函数的CFCC0、CFCC1 特征。上述特征在基于传统CFCC 特征提取基础上，仅改变了提取过程中的非线性幂函数，最后将其输入分类网络FcaNet-MobileNetV2 中进行分类识别，不同听觉特性函数识别准确率如表3 所示。

表3 不同听觉特性函数识别准确率

通过分析发现，在 5-～15 dB 信噪比下，本文所提非线性幂函数提取的FCFCC 特征参数语种识别准确率较文献[12]、文献[25]所提CFCC0、CFCC1以及传统CFCC 有一定的提升。与采用对数非线性函数来模拟听觉特性函数提取的LCFCC特征相比，其平均识别准确率提升了4.79%。实验说明了采用本文所提非线性幂函数模拟人耳听觉特性函数提取的FCFCC 特征参数在噪声环境下具有一定的抗噪性和有效性。

2) 实验2

为了验证本文提出的新型分数阶小波变换作为耳蜗基底膜上的耳蜗滤波函数所提取的NFCFCC 特征参数的稳健性，分别提取不同信噪比下CFCC 特征、MFCC 特征、GFCC 特征以及Fbank 特征，将其输入分类网络FcaNet-MobileNetV2 中进行分类识别比较，不同特征参数识别准确率如表4 所示。

从表4 可知，本文利用新型分数阶小波基函数来模拟信号在人耳基底膜上的运动过程，且引入能够反映声音强度的啁啾参数所提取的NFCFCC 特征较其他特征语种识别准确率有显著提升，与MFCC 特征相比其平均识别准确率提升了4.77%，与 CFCC 特征相比其平均识别准确率提升了6.58%。因此，采用引入啁啾参数的新型分数阶小波变换来模拟耳蜗滤波器能够有效地突破小波变换对信号进行时频域分析的缺陷，从而能够在时频域分析且在继承多分辨分析优点的同时对信号在时频与分数域进行多辨分析，进一步提升了特征参数的有效性与稳健性。

表4 不同特征参数识别准确率

3) 实验3

为了进一步提升改进特征参数的稳健性，在实验2 提取NFCFCC 特征算法的基础上，在特征提取前端引入自适应滤波对信号进行增强去噪，提取更具抗噪性的NFCFCCAF 和文献[12]所提基于谱减法与非线性幂函数的FFPSS 特征参数，分别在不同信噪比下采用分类网络FcaNet-MobileNetV2 进行语种识别准确率比较，不同特征识别准确率如表5所示，各语种在不同信噪比下的识别准确率如表6所示。

从表5 可知，在特征提取前端引入自适应滤波对噪声信号进行语音增强处理，再利用实验2提取NFCFCCAF 特征与文献[12]提取的FFPSS特征，分别在 -5～15 dB 信噪比下分别进行语种识别比较，NFCFCCAF 特征参数的语种识别准确率有显著提升。在低信噪比下，NFCFCCAF 特征较FFPSS 特征其平均识别准确率提升了2.47%，说明本文算法具有一定的抗噪性与可行性。对比表4 与表5 中NFCFCC 特征与NFCFCCAF 特征的语种识别准确率可知，引入自适应滤波降噪较未采用自适应滤波降噪所提取的特征显著提升了语种识别准确率，平均识别准确率提升了3.7%，且较传统CFCC 特征，其平均识别准确率提升了10.28%，提升了系统的稳健性。

表5 不同特征识别准确率

从表6 可知，5-～15dB 信噪比下各语种的识别效果较好，且识别准确率整体呈上升趋势。说明了采用本文算法对语音信号提取NFCFCCAF 特征再利用FcaNet-MobileNetV2 网络进行分类识别能够更好地提取语种之间的相关信息并且达到了较好的区分度。在低信噪比下，相较于其他语种，法语的语种识别准确率较低，平均识别准确率达80%，而英语的识别准确率最高，平均识别准确率达88%。这说明法语提取的文本特征区分性较其他语种并不高，而英语提取到的文本特征参数区分性最高。

表6 各语种在不同信噪比下的识别准确率

4) 实验4

由于NFCFCCAF 特征参数所表征的为语音信号的静态特征，并不能较好地表现出语音的实际动态特性。为测试本文所提NFCFCCAF 的语种识别有效性，求取NFCFCCAF 特征参数的一阶差分系数[24]、再与NFCFCCAF 特征进行融合处理得到融合特征NFCFCCAF-DS。

为了验证本文所提分类网络FcaNet-MobileNetV2 的识别性能，采用不同的分类网络 FcaNet-MobileNetV2、MobileNetV2 以及ResNet[24]对特征参数进行分类识别。其识别结果如表7 所示。

从表7 可知，在-5～15 dB 信噪比下，不同特征在不同分类网络中都表现出较好的识别效果。在FcaNet-MobileNetV2 分类网络中，2 种特征平均识别准确率达83.05%和85.65%；在MobileNetV2 分类网络中，2 种特征平均识别准确率达81.04%与83.6%。在这2 种特征下FcaNet-MobileNetV2 网络较MobileNetV2 网络平均识别准确率提升了2.01%与2.05%。这说明经过引入频域注意力机制使整个网络模型能够集中捕捉特征中的频域信息，加强了特征判别的指向性，提升了网络的识别性能。

表7 不同特征在不同分类网络中的语种识别准确率

在ResNet 分类网络中，2 种特征平均识别准确率达81.30%和82.27%，FcaNet-MobileNetV2 网络较ResNet 平均识别准确率提升了1.75%和3.38%。说明基于倒残差结构FcaNet-MobileNetV2 网络能够有效处理小样本，且提取到特征中更多的高维信息以及频域信息，避免了特征信息损失，弥补了基于残差结构的ResNet 对于小样本中不能有效提取整体特征足够多的信息缺陷，验证了FcaNet-MobileNetV2 网络的可行性与识别优越性。同时通过不同的分类网络也验证了本文算法所提取特征参数的有效性。

另外，从本文所提NFCFCCAF 特征参数与加上反映其动态特性的NFCFCCAF-DS 特征参数在不同信噪比下的语种识别准确率可知，在3 种分类网络下，NFCFCCAF-DS 动态特征参数的识别准确率都要高于静态特征NFCFCCAF 的识别准确率。且在FcaNet-MobileNetV2 分类网络下动态特征较静态特征平均识别准确率提升了2.6%，特别在-5 dB 信噪比下语种识别准确率提升了5.7%。这说明NFCFCCAF-DS 特征参数在低信噪比下能够有效反映出语音信号局部特征动态特性，同时有效表征语音信号的完整特性，具有较好的稳健性。

5 结束语

针对低信噪比下语种识别准确率低与稳健性差的问题，提出了一种结合自适应滤波与分数阶小波变换的耳蜗倒谱系数提取算法。实验采用自适应滤波对语音信号进行噪声滤除，再将新型分数阶小波变换作为小波基函数来模拟信号在耳蜗基底膜上的运动，然后通过模拟人耳听觉过程提取出NFCFCCAF 特征参数，最后将提取出的特征参数作为FcaNet-MobileNetV2 网络的输入进行分类识别。实验对比了传统CFCC 特征以及近几年经典的Fbank 等特征，本文算法的识别准确率都有显著提升，相较于传统 CFCC 语种识别性能提升了10.28%，有效改善了传统特征在低信噪比下识别准确率低的问题，具有较强稳健性，且更具抗噪性，提高了语种识别准确率。由于本文实验只针对特征提取进行改进，因此在未来的研究中，需要加强对语种识别的模型研究，以进一步提升语种识别性能及稳健性。