基于卡尔曼滤波的太阳跟踪装置控制策略

李浩楠，李其轩，倪 瓒，赵 品，郑大林，原晓楠

（西安交通大学电气工程学院，西安 710049）

0 引言

提高太阳跟踪的精度与稳定性是提高光伏发电效率至关重要的一环，目前太阳跟踪装置主要有：基于光敏传感器的跟踪装置［1-2］；基于视日运动轨迹的跟踪装置［3-4］。光敏跟踪精度较高，但在太阳辐射强度减弱时跟踪精度降低，而且会受到局部强光的干扰；视日运动跟踪稳定，但依赖于算法的精度与复杂度，且缺少反馈作用，需要定期维护校准［5］。对此，部分学者研究优化视日运动跟踪算法［6-8］，也有学者综合两种跟踪方式，提出混合式跟踪方法［9-11］，以期低成本高精度跟踪太阳，提高光伏发电效率。本文以视日运动跟踪原理为基础，基于卡尔曼滤波算法提出4 种太阳跟踪装置的控制策略，以期在保证跟踪系统稳定性的基础上提高光伏发电系统的光接收功率，从而提高光伏发电系统的发电效率。

1 视日运动跟踪原理

1.1 赤道式跟踪

赤道式跟踪使用赤道坐标系，如图1 所示。图中：δ为赤纬角，是地球中心与太阳中心连线和赤道平面的夹角，北半球为“+”，南半球为“-”；θ 为时角；Q点取为天赤道与观测者的天顶以南那段子午圈的交点，则从Q点起沿天赤道到天球上一点的赤经圈与天赤道交点的弧长称为时角，向东为负，向西为正。

图1 赤道坐标系

基于赤道坐标系进行太阳赤纬角和时角估计的算法研究，从而确定太阳的位置。其中，Stine公式［12］：

式中：δ为赤纬角；n为所求日期，是1 a中的第n天。

规定正午时角θ ＝0，上午θ ＜0，下午θ ＞0，其中：

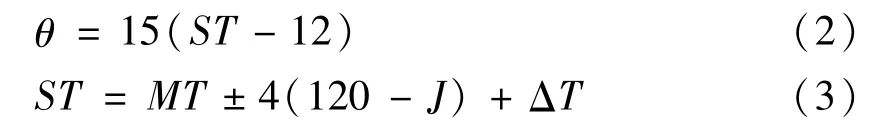
式中：ST为真太阳时；MT为北京时间；J为当地位置所在经度，东经取-，西经取+；ΔT为时差。

对于时差估计的Stine公式［12］：

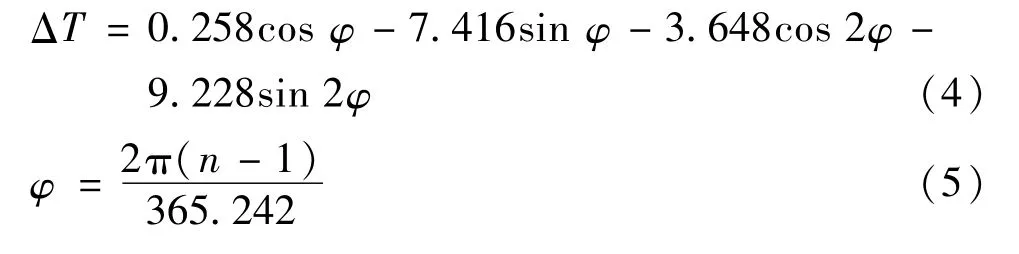
1.2 地平式跟踪

地平坐标系如图2 所示，其中α为高度角，β 为方位角，通过算法研究确定这2 个参数即可确定太阳某一时刻所处的位置。

图2 地平坐标系

地平式跟踪算法与赤道式跟踪相同，仅进行了坐标变换，可得：

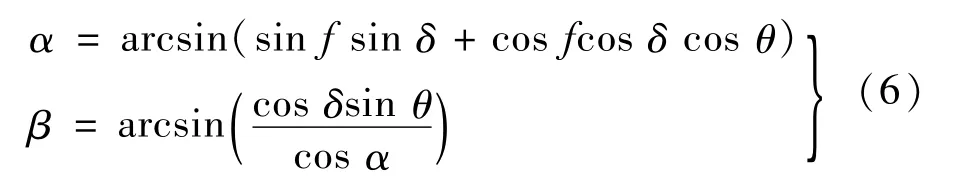
式中，f为观测地纬度。

2 太阳跟踪控制系统结构

本文设计的太阳跟踪控制系统原理框图如图3 所示。基于不同的传感器、执行器和太阳跟踪方式选择，设计并研究了4 种不同的太阳跟踪装置的控制策略。

图3 太阳跟踪控制系统原理框图

2.1 传感器选择

（1）硅光电池传感器。硅光电池是由半导体单晶硅构成的，具有光电转换的性质，其光生电流与光强成正比。本文设计了一种由2 个相同参数的硅光电池制作的传感器，其三维模型如图4 所示，其中黑色部分为硅光电池板；白色部分为硅光电池固有封装；灰色部分为附加外壳，起遮挡太阳光的作用。设两片硅光电池长与宽分别为a、b，传感器顶端到硅光电池表面距离为h。

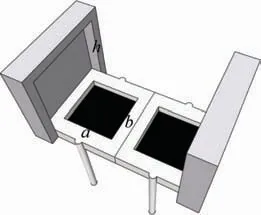
图4 硅光电池传感器三维模型

硅光电池传感器纵截面如图5 所示，左侧硅光电池电流记为i1，右侧硅光电池电流记为i2。由硅光电池数学模型［13］可得测量电流与太阳位置与传感器法向夹角的关系为

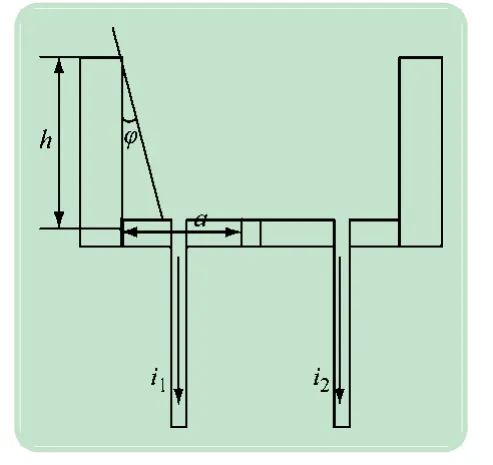
图5 硅光电池传感器纵截面

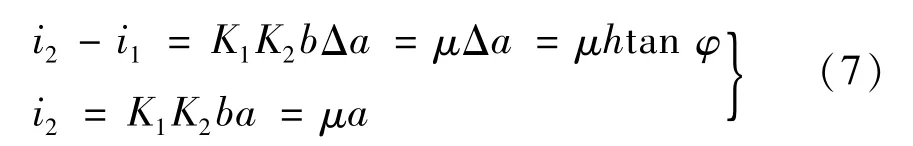
式中：K1为单位面积受光强度，W／m2；K2为光电转化系数；φ为太阳位置与传感器法向夹角，而且由于尺寸限制不能太大；a为硅光电池长；Δa为阴影部分长度；b为硅光电池宽；h为传感器顶端到硅光电池板表面距离。电流经信号调理上传给控制器可以得到φ。

（2）姿态传感器。本文需要的姿态传感器包括三轴加速度计、三轴陀螺仪和三轴磁力计。分别能够测量物体的加速度、绕轴旋转角速度和空间中的磁感应强度，数据融合可以得到运动转台的高度角、方位角。

（3）GPS模块。GPS模块可获得来自卫星的世界标准时间信号，并得到当地的经度J和纬度f，用于计算某时刻太阳赤纬角、时角、方位角与高度角。

2.2 执行器选择

赤道式单轴跟踪太阳转台模型如图6 所示，地平式双轴跟踪太阳转台模型［14］如图7 所示。电动机可选用步进电动机或者伺服电动机。

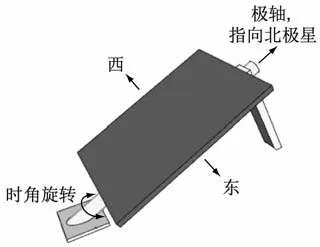
图6 赤道式太阳转台机械结构

图7 地平式太阳转台机械结构

3 太阳跟踪控制策略

3.1 增量控制的赤道式跟踪

（1）控制系统设计。增量控制的赤道式跟踪控制系统原理框图如图8 所示，采用硅光电池传感器测量太阳位置与光伏板法向夹角，通过GPS 输出的时间与纬度结合赤道式算法得到当前应调整的赤纬角和时角的状态估计值，再由控制器计算得到卡尔曼滤波值，从而控制步进电动机增量，使光伏板跟踪太阳位置。

图8 增量控制的赤道式跟踪系统设计原理框图

（2）系统建模。

①状态估计建模。由赤道式跟踪算法的分析可知，赤道式跟踪中仅跟踪太阳时角，太阳赤纬角变化缓慢，属于人为定期调节。时角变化主要是视太阳时变化，由于某些天文学因素，会引起地球自转不匀速［15］，因此时角动力学方程

式中：ε（t）为布朗运动；φ ＝15°／h。对式（8）离散化，建立该系统的增量状态方程：

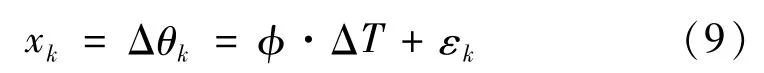
式中：ΔT为采样时间；xk为状态量，即Δθk为地球在第k个ΔT内自转角度，也即太阳第k个ΔT内时角增量，也即步进电动机在k时刻的控制增量；εk为高斯白噪声，服从εk～N（0，Q）；Q值与跟踪算法和采样时间ΔT均有关。

②测量方程。系统使用硅光电池传感器，与光伏板平行放置，可以反馈电动机即将转动前光伏板位置和太阳位置的角度偏差，也即Δθ，因此，测量方程为

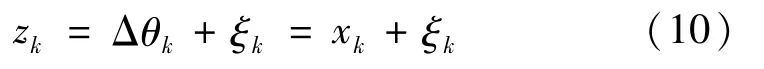
式中：ξk～N（0，R），为传感器测量噪声，R值与传感器精度和实际环境有关；zk为第k次传感器测量值，且εk，ξk互不相关。

（3）卡尔曼滤波。选取测量值为初始值，通过硅光电池传感器可以测得初始的系统状态量Δθ0，则

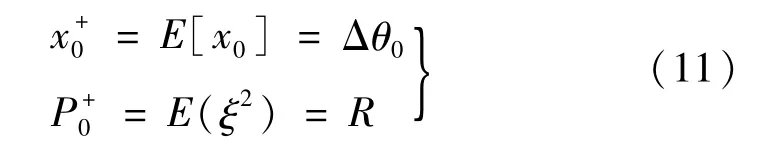
状态方程一步预测值为

测量更新后的卡尔曼滤波值为

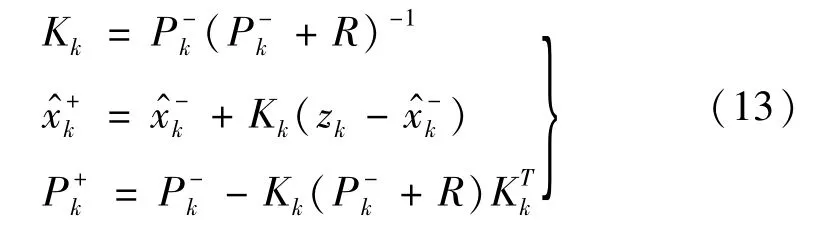
式中：Pk为协方差矩阵；Kk为卡尔曼增益。

（4）仿真分析。基于Matlab 对所设计的算法进行仿真分析，仿真5 ×103s内对时角跟踪的情况，测量周期设为60 s，初始值选取-60°，仿真结果如图9所示。

图9 增量控制的赤道式跟踪仿真结果

从图9 可以看到，卡尔曼滤波值对于太阳时角实际位置和光伏板法向的夹角的跟踪效果好，光伏板法向基本与太阳位置重合。对于该夹角，仅传感器追踪值、仅跟踪算法跟踪值和卡尔曼滤波跟踪值与真实值的误差平方和分别为2.822，1.503，1.089。由仿真结果可知，卡尔曼滤波追踪误差更小，精度更高。

3.2 增量控制的地平式跟踪

（1）控制系统设计。增量控制的地平式跟踪控制系统原理框图如图10 所示，采用2 个硅光电池传感器分别测量太阳转台对应高度角和方位角与太阳位置的夹角，三轴磁力计得到真北方向，通过GPS 输出的时间与经纬度，由地平式跟踪算法得到状态估计值，由控制器计算得到卡尔曼滤波值，控制步进电动机增量，使光伏板跟踪太阳。

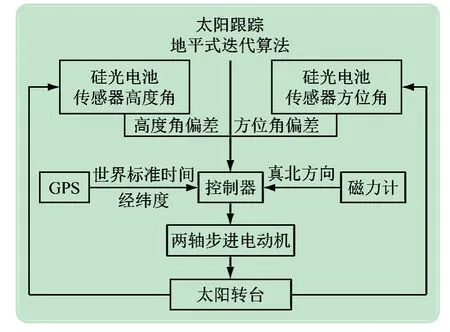
图10 增量控制的地平式跟踪系统设计原理框图

（2）系统建模。

①状态估计建模。地平式跟踪电动机同时跟踪高度角与方位角，由地平式跟踪的分析可知，方位角与高度角依赖于时角与赤纬角，由于太阳赤纬角δ 变化缓慢，在1 d内视为恒定量，系统简化为依赖于时角的定常系统，由时角分析与式（6）、（8）可以得到：

将式（14）离散化，根据式（9）及扩展卡尔曼滤波线性化思想，对方程线性化得到：

②测量方程。系统中两个硅光电池传感器安装均与光伏板平行，分别测量高度角与方位角光伏板与太阳位置夹角，即Δα，Δβ，因此，测量方程为

式中：ξi～N（0，R），i＝1，2，且ξ1，k，ξ2，k独立，分别为两个传感器的测量噪声；Hk为测量矩阵，且εk，ξk互不相关。

（3）卡尔曼滤波。由状态方程（15）可以得出初始的状态量Δθ0＝φ·ΔT，则

状态方程一步预测值为

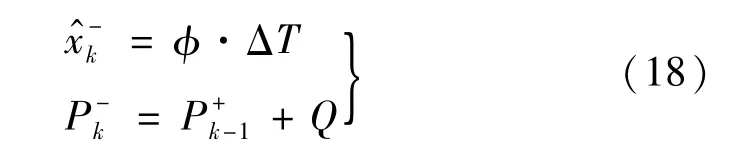
线性化参数得到：

测量更新后的卡尔曼滤波值为

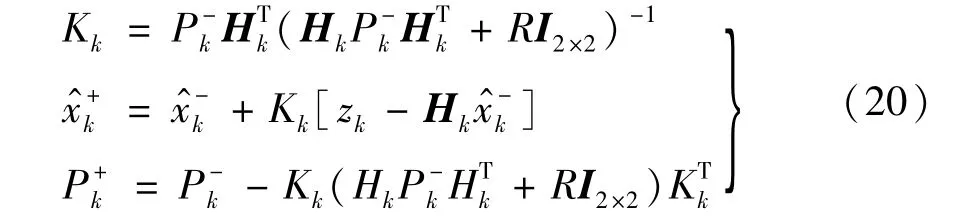
式（17）、（18）和（20）中Pk为协方差矩阵；Kk为卡尔曼增益。

（4）仿真分析。选择1 a中第216 d，仿真5 ×103s内跟踪的情况，采样周期设为60 s，初始值选取-60°，仿真结果如图11 所示。

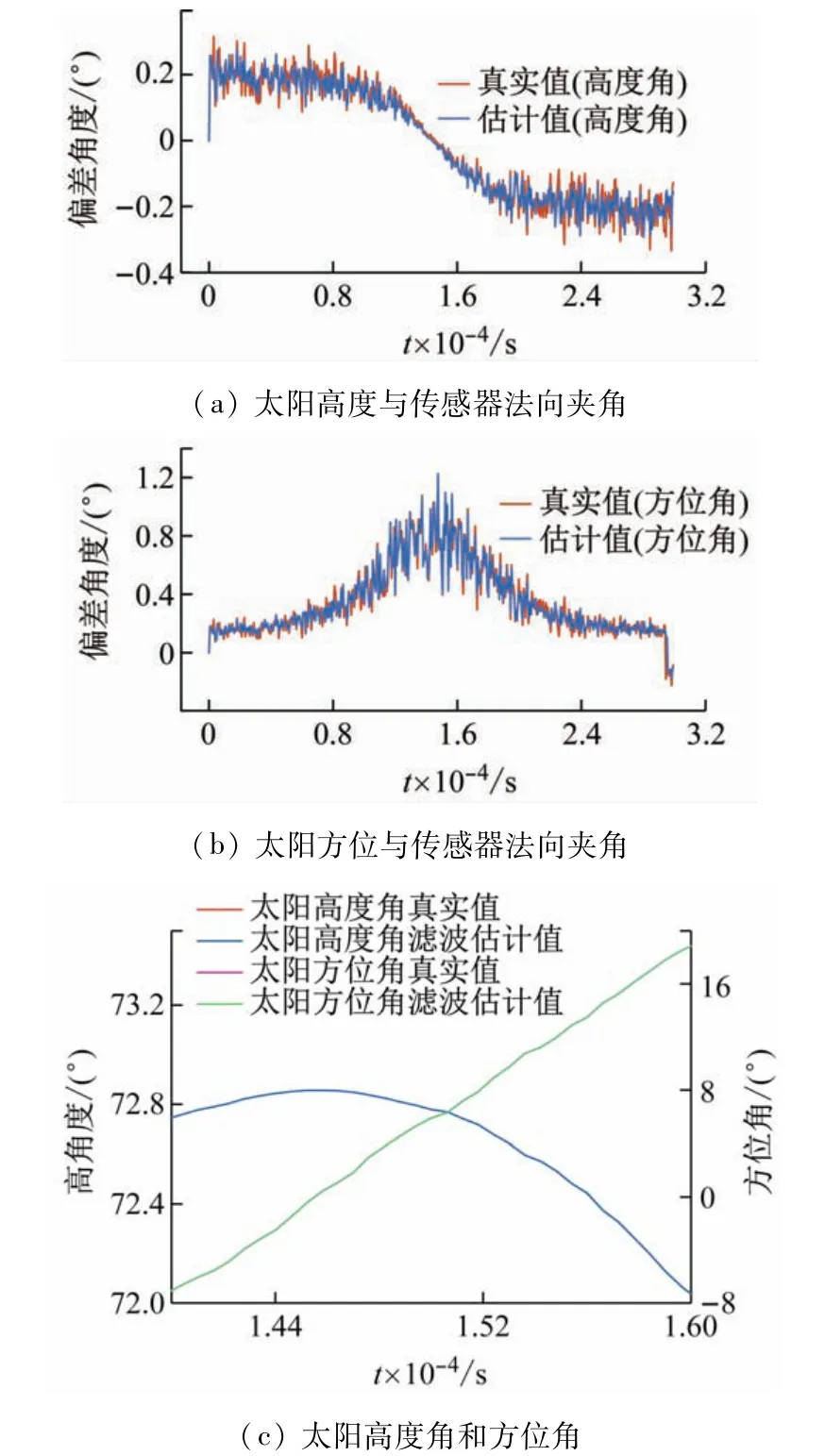
图11 增量控制的地平式跟踪仿真结果

从图11 中可以看到，卡尔曼滤波值对于太阳高度角和方位角实际位置和光伏板法向的夹角的跟踪效果好，光伏板法向基本与太阳位置重合。对该夹角仅传感器追踪值、仅跟踪算法跟踪值和卡尔曼滤波跟踪值与真实值的误差平方和结果如表1 所示。

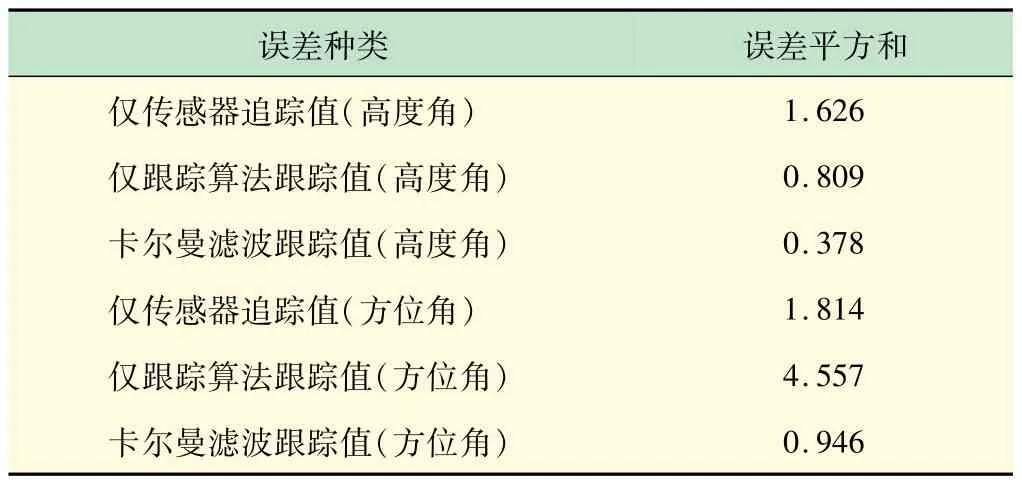
表1 增量控制不同跟踪方式误差结果对比

高度角和方位角跟踪均是卡尔曼滤波跟踪的误差平方和最小。由仿真结果可知，卡尔曼滤波追踪误差更小，精度更高，效果更好。

3.3 位置控制的赤道式跟踪

（1）控制系统设计。位置控制的赤道式跟踪控制系统原理如图12 所示，采用硅光电池传感器测量光伏板与太阳位置的夹角，伺服电动机编码器反馈得到的电动机位置值，通过机械结构映射到赤道坐标系，可以得到太阳时角测量值，由赤道式跟踪算法可以得到时角估计值，由控制器计算得到卡尔曼滤波值，控制伺服电动机位置。

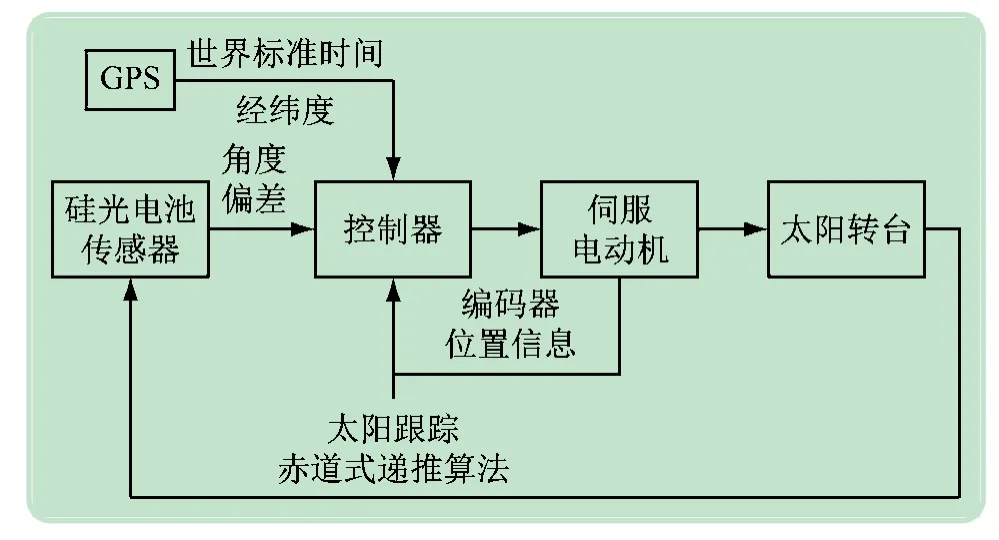
图12 位置控制的赤道式跟踪系统设计原理

（2）系统建模。

①状态估计建模。根据赤道式跟踪的分析对式（8）离散化处理，得到该系统位置状态方程为

式中，θk为k时刻太阳时角。

②测量方程。伺服电动机可以由编码器得到当前角度位置，通过机械结构和姿态传感器值可以得到光伏板当前对应的时角，硅光传感器作用与3.1（2）小节相同，因此，传感器测量方程为

式中：ξk～N（0，R），为传感器测量噪声；zk为k时刻太阳时角测量值，且εk，ξk互不相关。

（3）卡尔曼滤波。系统由GPS 读取初始时间和当地经纬度，可以计算得初始的状态量θ0，可以得出：

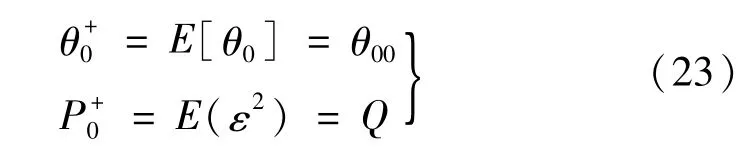
令xk＝θk，滤波过程与式（12）、（13）相同。

（4）仿真分析。仿真5 ×103s 内跟踪的情况，采样周期设为60 s，初始值选取-60°，仿真结果见图13。

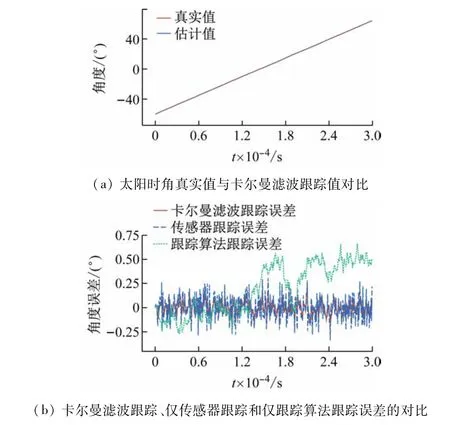
图13 位置控制的赤道式跟踪仿真结果

对于太阳时角，仅传感器追踪值、仅跟踪算法跟踪值和卡尔曼滤波跟踪值与真实值的误差平方和结果如下：6.321，50.114，2.116。由仿真结果知，卡尔曼滤波追踪对太阳时角的跟踪误差更小，精度更高。

3.4 位置控制的地平式跟踪

（1）控制系统设计。位置控制的地平式跟踪控制系统原理见图14，采用两个硅光电池传感器分别测量太阳转台对应高度角和方位角与太阳位置的夹角，由姿态传感器得到转台当前方位角与高度角，由地平式跟踪算法得到状态估计值，由控制器计算得到卡尔曼滤波值，控制伺服电动机位置，使光伏板跟踪太阳。

图14 含位置反馈的地平式跟踪系统设计原理

（2）系统建模。

①状态估计建模。根据方程与式（6）可以得出本系统位置状态方程为

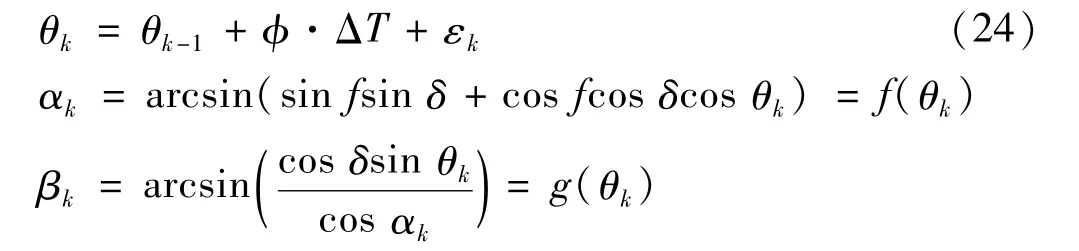
输出量为非线性，状态量变化为线性。

②测量方程。通过各坐标轴平行安装在光伏板上的姿态传感器，可以获取当前光伏板的高度角、方位角，硅光电池传感器可以获取光伏板位置和太阳位置的高度角与方位角偏差，即Δα、Δβ，因此，测量方程为

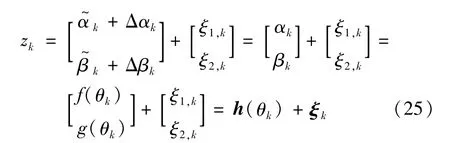
式中：ξi～N（0，R），i＝1，2，且ξ1，k、ξ2，k独立，分别为两组传感器的测量噪声，且εk、ξk互不相关。

（3）卡尔曼滤波。由GPS 读取初始时间和经纬度，结合地平式算法，可以计算得初始的状态量θ0，故：

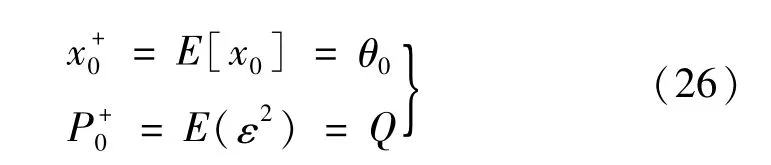
令xk＝θk，状态量一步预测同式（18），由扩展卡尔曼滤波线性化可以得到：

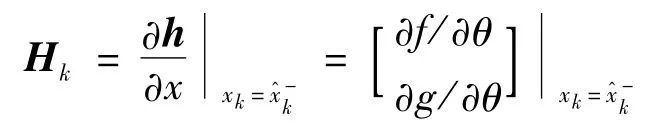
测量更新卡尔曼滤波过程与式（20）相同。

（4）仿真分析。选择1 a中第216 d仿真5 ×103s内跟踪的情况，测量周期设为60 s，初始值选取-60°，仿真结果如图15 所示。

图15 位置控制的地平式跟踪仿真结果

对太阳高度角和方位角，仅传感器追踪值、仅跟踪算法跟踪值和卡尔曼滤波跟踪值与真实值的误差平方和结果如表2 所示。

表2 位置控制不同跟踪方式误差结果对比

由仿真结果可知，对太阳高度角和方位角的卡尔曼滤波追踪误差均更小，精度更高，效果更好。

4 结语

通过分析现有太阳跟踪装置的优缺点及多种太阳跟踪原理，根据视日跟踪原理采用多种传感器结合算法设计与优化进行了太阳跟踪装置控制策略研究。基于卡尔曼滤波算法，同时考虑模型误差与传感器噪声，设计了4 种太阳跟踪装置控制系统，并利用MATLAB进行了仿真分析，仿真与计算结果表明所设计的4 种太阳跟踪装置的跟踪精度得到明显提高。同时，所提出的控制策略同时利用太阳跟踪模型数据与传感器测量数据，可以消除视日运动轨迹跟踪的算法误差，通过调节参数一定程度上克服光电跟踪弱光条件下的不准确问题，采用多种传感器，可以对不同环境和位置进行稳定精确的太阳跟踪，能够在保证跟踪系统稳定性的基础上提高光伏发电系统的初端接收功率，从而提高光伏发电系统的发电效率，具有广泛的应用意义。