基于Bayes-MCMC 的水声双程信道建模及自适应采样反演

赵 罡 ,孙乃葳 ,申 珅 ,杨益新

(1.西北工业大学 航海学院,陕西 西安,710072;2.中国船舶集团有限公司 第705 研究所,陕西 西安,710077)

0 引言

迄今为止声脉冲仍是水下通信及目标探测的主要手段。在水下传播过程中,受信道多径及目标闪烁等多种因素的作用,声脉冲信号会发生衰落和起伏等变化,这一变化对工作在浅海水域的鱼/水雷等主战武器,以及无人水下航行器(unmanned undersea vehicle,UUV)、微型潜艇、蛙人探测声呐等水下特种装备的作用尤其显著,对水下通信质量及目标检测有效性带来较大影响[1-3]。为消除这一影响,人们在针对水声衰落信号的自适应处理方面开展了较多工作[4-5],但对于提供验证环境相关的仿真方法和模型研究却所做不多。实际水声信道衰落情况复杂多变[6],外场试验本身又存在成本高昂难以开展的问题,在包括鱼/水雷、UUV及特种作战装备在内的声探测武器研发过程中,使用外场试验的方式对信号处理方法进行改进和验证显然是不现实的。考虑到信噪比(signal noise ratio,SNR)在目标检测中的重要性[7],建立与实际情况有较高符合度的水声双程信道目标回波时域起伏仿真模型,并提供一种可有效利用实航数据的模型参数反演方法,是水下目标精细回波仿真所必须考虑的问题,在水下声探测武器的研制过程中具有重要的意义。

1 水声双程信道建模

首先以经典水声单程信道模型为基础进行双程信道模型的建立: 考虑到一定时空不变条件下信道的对称性将去程信道与返程信道特性等同,然后在直达和多径信号强度2 个方向,通过积分计算二者联合的全概率表达式,最后建立收发同置应用背景下的水声往返双程信道模型。

1.1 单程信道基本模型

水声信道的信号传输主要受界面、介质和障碍物的反射、衍射等作用,其信道物理过程复杂,难以解析描述,常利用经验数据拟合概率分布函数来表示信号幅度变化等重要特征,针对水声环境特点,可通过直达信号和多径信号的加性合成来表示,即

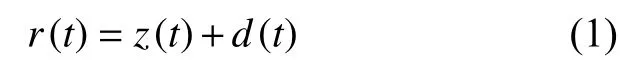
式中:z(t)为直达信号;d(t)为多径信号。

鱼/水雷、UUV 及特种作战装备常用高频短脉冲作为目标声源探测信号,其频率高且传播距离较近,因此开展信道物理过程复杂性建模时可做如下合理假设: 1)信道的直射分量受水体中障碍物遮挡的影响远小于界面反射的多径效应;2)传播衰减造成的短脉冲内慢起伏可忽略。此时可认为z(t)保持包络不变、而d(t)受界面及温度梯度的影响变化明显,则r(t)符合Ricean 分布且满足条件概率分布

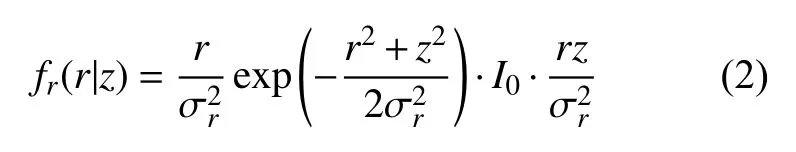
式中: 忽略时间参量t;表示d(t)平均散射功率;I0(·)表示第1 类零阶修正贝塞尔函数。

1.2 双程信道模型

双程信道模型的建立需联合考虑信号去返2 次行程,即分别设定r1(t)、r2(t)为去程信号和返程信号,则二者对应的直达和多径成分满足

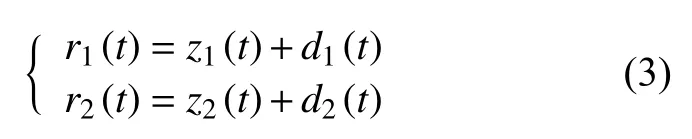
r2(t)是由水下目标体对去程信号r1(t)反射产生的,故其直达成分z2(t)的包络与目标反射特性相似呈对数正态分布,可用r1(t)的条件概率表达,即

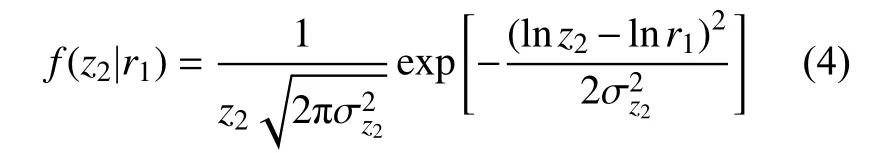
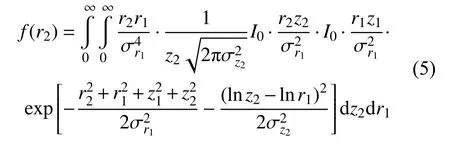
其中,表示去程信号的平均散射功率。

文中所用实航数据以声周期方式保存,相对于声在水中传播时1 个声周期寻的短脉冲时间片段内可认为目标回波过程是确定的,其强度并不发生闪烁,此时双程水声信道模型可简化为

2 水声双程信道参数反演算法

水声双程信道参数的反演问题中,非启发式的非线性反演方法如遗传算法(genetic algorithm,GA)、粒子群算法(particle swarm optimization,PSO)等受算法本身设计限制只能以概率密度函数(probability density function,PDF)差异作为代价函数开展反演[10],其对实航数据时域真值信息利用不足。为有效利用实航数据时域采样先验结果[11],流程中以马尔科夫链蒙特卡洛(Markov chain Monte Carlo,MCMC)方法为主要方法实现水声双程信道模型抽样,并进一步结合Bayes 方法的最大后验估计(maximum a posteriori,MAP)完成参数反演过程,而反演参数的有效性判断主要通过全局误差评价模型对比分析海试数据、反演结果分布特性差异来进行。水声双程信道反演算法基本流程如图1所示。

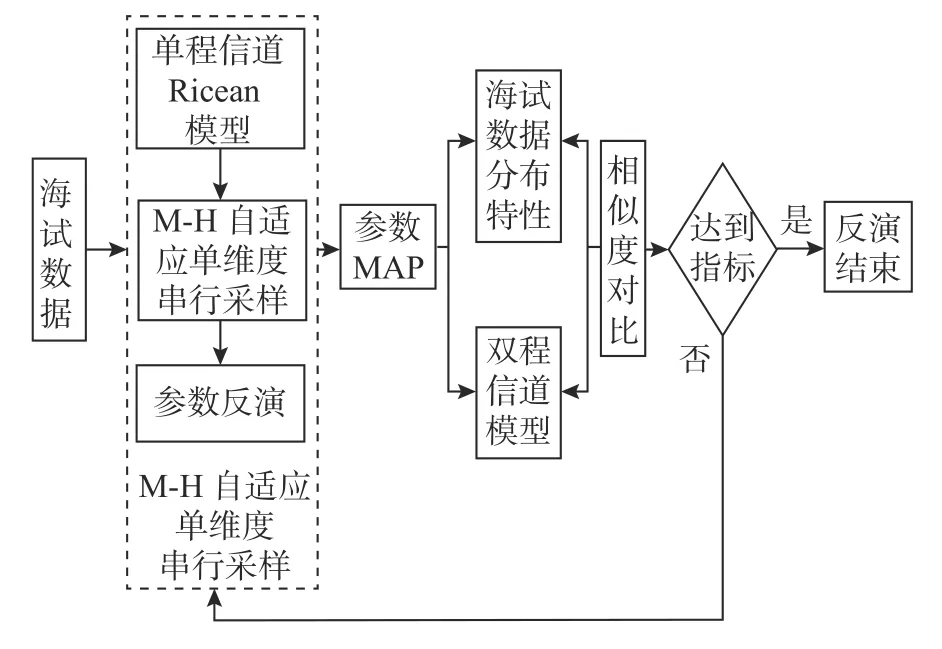
图1 水声双程信道反演算法基本流程Fig.1 Basic process of underwater acoustic go-back channel inversion algorithm

一般而言,Bayes-MCMC 反演的基本思路是通过采样构造一条在给定真值样本条件下稳态分布服从所需模型参数向量后验概率密度的马尔科夫链,当数据链收敛时使用采样数据计算所求模型参数集的各矩特征量,数据链同时作为以反演结果为参数的正演模型数据样本[12]。MCMC 方法的核心在于构造转移核接收函数,其设计原则与采样器直接相关,最为通用的采样器包括Metropolis-Hastings(M-H)、吉布斯采样(Gibbs sampling,GS)方法等。GS 方法作为M-H 方法的特例是对参数集逐一完成单维度正交采样,其效率虽然较高但要求准确的参数条件建议分布,而水声反演问题往往准确的模型参数向量先验条件概率密度难于确定;M-H 方法使用任意建议分布在整个参数集空间整体采样以生成数据样本,且建议分布取对称分布时可进一步简化转移核接受函数形式,具有较好的实现性,因此文中采用M-H 采样方法[13]。

由于双程信道实航数据分布特性已知的情况与通常MCMC 采样先验概率未知的假设条件不同[14]: 当先验概率未知时,MCMC 采样一般是独立并发抽取2 组随机序列,并以2 组序列收敛情况一致性作为停止采样的判据[15],或者通过对数据采样过程的设计达到降低计算量提高反演效率的目的[16-17];而双程信道实航数据分布特性已知时,可据此对每次抽取结果的有效性进行判断,并使用抽样分布与实航数据分布的绝对差异或相似程度作为采样状态改变的判定条件。结合图1 反演算法特征和M-H 采样存在参数多维耦合条件下命中效率低的问题,为保证数据的高效抽样,文中基于MCMC 进行了优化,提出一种M-H 自适应单维度串行采样算法,即通过M-H 方法进行精度自适应调节的单维度串行采样过程。

首先给出如下定义: 定义模型参数向量m={m1,m2,···,mn}的取值空间为 ℜ;定义m中mi的补集为∁mmi={m1,m2,···,mi-1,mi+1,···,mn}。

具体反演算法步骤如下:

1)设定目标反演偏差 εT、反演偏差增量 Δε、最大反演次数Rm,初始化反演偏差ε0=∞、反演次数Rc=0、反演参数序号i,j=1;

2)在 ℜ上随机抽取或采用全局寻优方法生成模型参数向量m={m1,m2,···,mn};

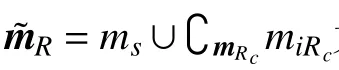
4)对每一个被接受的模型参数ms,使用计算模型正演PDF;

5)对模型正演PDF 及真值PDF 进行同步离散采样并计算其面积误差ε,当不满足误差收敛条件即ε ＞ε0时回到步骤3);否则接受,同时令i=i+1 及ε0=ε;

6)判断 εT与 ε0关系: 若ε0＜εT,即目标反演偏差已经达到,则令m=并停止反演;若εT＜ε0,则令m=,同时判断若i＜n,即尚有模型参数分量未执行M-H 采样,则回到步骤3);否则反演次数Rc加1,同时令i=1;

7)当Rc＞Rm时即达到单轮最大反演次数时,为避免陷入局部优化令εT=εT+Δε进行反演精度调整,并将反演次数计数置0 后回到步骤3);否则直接回到步骤3)。

算法步骤1)中的各初始设定参数的选择可根据反演时预期的结果精度设定,但精度要求越高、反演次数越多,虽然会得到更为精确的反演结果,也会带来更大的计算压力,对算法执行效率产生影响;算法步骤3)中的对称分布仅仅是为满足简化M-H 采样接受条件的需求,常用如均匀分布、高斯分布等都可使用。总而言之,基于MCMC 方法的M-H 自适应单维度串行采样算法可综合考虑精度和效率因素,通过初始参数设置灵活控制参数采样过程,且在算法终止条件上通过对全局优化代价函数结果的判断以达到有效收敛的目的,可以有效避免因初始参数设置不当而引起的反演结果偏差过大的问题。

3 反演算法有效性验证

3.1 反演模型仿真设计

为验证反演算法的有效性,首先对经典分布模型参数进行反演验证。Ricean 分布是描述海洋信道时常用的统计模型,当使用直达信号与多径信号功率比即K因子进行描述时其表达式为

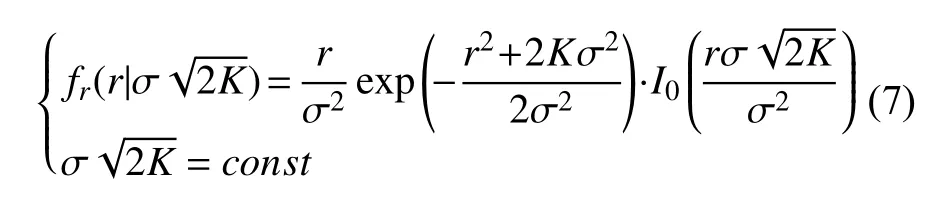
此时反演模型流程步骤中参数MAP 估计的主要任务是完成参数和K的估计。记真值样本为Si,构建Ricean 模型参数反演转移核接受函数为

式中,Ri(m1)及Ri(m2)为符合式(7)在设定模型参数条件下的离散化采样结果,其中m1和m2分别代表迭代采样过程中前后2 次由σ和K构成的参数向量。

由于各采样独立,v为各维数据误差协方差矩阵Cd特征值积乘,通常可使用GA、模拟退火(simulated annealing,SA)、PSO 等全局寻优方法获取极大似然估计。考虑到文中方法Cd矩阵是由真值和采样数据PDF 函数值残差构成,同时方法本身存在参数收敛性判断,且v值与数据矩阵相似性反向相关在反演过程中逐渐趋小,因此可在收敛性判断同时进行v的迭代更新,而其初值只需在0～1 范围任意取值即可,不失一般性可将v设定为1。

3.2 仿真收敛条件设计

常规MCMC 反演一般采用针对2 组独立并行采样序列的非参数检验方法,如Kolmogorov-Smirnov(K-S)检验等的结果作为收敛判断和算法终止条件,但在文中方法中MCMC 作为参数采样过程主要用于提高采样效率,而对反演过程的终止条件判断可针对整体反演结果进行评价。基于此,设计针对模型参数反演结果的全局误差模型如下

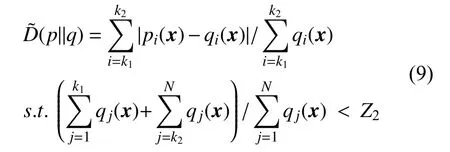
式中:p、q分别代表反演及真值样本数据PDF,(p||q)代表2 个PDF 全局差异程度,当其小于εT时,认为反演目标达成,终止采样,进行上述判断的参数区间取Z2即二西格玛水平(2-Sigma Level)。

全局误差模型可对仿真采样结果进行定量评价,但对于多组采样及反演结果还需要有相似性的定性评价。在机器学习中,KL(Kullback-leibler)散度常用来对2 个概率分布的相似性进行评价,其定义为

KL 散度越小,代表2 个分布越相似,2 个相同分布的KL 散度值为0。文中将直接使用KL 散度指标对多组反演全局误差模型计算结果进行定性评价。

3.3 算法验证

3.3.1 信道模型真值样本生成及评价

在水深一定的条件下,对于几公里内较近的传输距离,由于直达信道的存在以及多途情况不那么严重,以Ricean 描述的水声信道表现为较小的σ值和较大的K值。取一组典型值采用MCMC 采样方法生成符合由该组参数定义的Ricean 分布仿真样本如图2(a)所示,纵坐标r为采样信号幅值;其采样结果及其与真值PDF 和累积分布函数(cumulative distribution function,CDF)对比如图2(b)和图2(c)所示,其中纵坐标p为某幅值信号出现概率。

图2 MCMC 采样结果及其与真值分布对比Fig.2 MCMC Sampling results and comparison with their true distributions

仿真结果分析表明,与真值模型设定参数相比,各组采样均可较快收敛。σ2参数仿真结果误差0.4%,K参数仿真结果误差0.5%,PDF 全局误差1.2%。仿真采样生成的Ricean 分布样本与设定模型具有较高一致性,可以作为参数反演真值。

3.3.2 信道模型参数反演

使用所设计参数抽样及结果评价模型,以上节所生成数据样本作为真值对Ricean 分布模型参数开展反演,为比对反演结果将上节给定参数PDF作为拟合结果。反演设定条件为: 目标反演偏差εT=1%、反演偏差增量Δε=1%、最大反演次数Rm=5;每趟次参数采样数5 000 个。

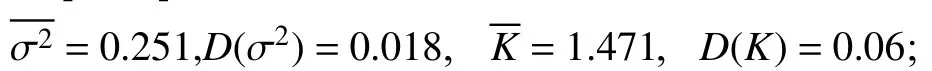
参数迭代反演过程以及结果对应的Ricean 分布PDF/CDF 与真值分布对比如图3 所示。

图3 模型参数采样过程及反演结果与真值分布对比Fig.3 Sampling process of model parameter and comparison of inversion results with true distributions

反演结果分析表明,与正演模型设定参数相比,参数 σ2反演结果误差为0.8%,参数K反演结果误差为1.5%,PDF 全局误差为2.6%。各参数均有较好的收敛一致性,单维度串行采样模型具有较高的反演精度和效率,可用于水声双程信道模型参数反演。

4 反演模型实测数据验证

4.1 真值样本预处理

不同于单程信道测量信号,水下自导武器声寻的脉冲通常为矩形或梯形包络的脉冲信号,其长度一般在10 ms 量级,而回波脉冲受传播、吸收衰减及信道衰落等作用,在接收端信号幅值往往较低并常采用时变或自动增益技术以提升其SNR,这些因素的影响在信道模型参数反演时都需考虑。一般来说,为了得到原始信号数据,需要基于补偿曲线消除增益作用影响,同时为了得到较为准确的脉冲起始和终止时刻,副本相关等基本信号处理过程也是必须的。

在一段实际回波信号中选择出反演所需的脉冲回波后,还需要对信号进行幅值归一化处理,同时考虑到采样及计算均在离散点上进行,所选择PDF 值域及积分计算值域范围均会对结果带来一定的影响。即使经过了预处理过程,受水文及界面环境的影响,弱回波脉冲信号被本底噪声部分淹没,仍会对反演结果带来一定的影响,下面的反演就是针对SNR 条件不同的几组回波展开的。以某湖上试验数据为例,采样时信道传输距离为500～2 000 m,2 组不同SNR 条件真值采样如图4 所示。

图4 不同SNR 下脉冲回波时域信号Fig.4 Pulse echo time domain signals under different SNRs

4.2 反演模型设计

反演过程的M-H 抽样模型转移核接受函数形式及参数定义同式(8),不同之处在于符合设定模型参数的离散化采样结果生成时,采取式(6)所定义不考虑目标闪烁条件的水声往返双程信道时域起伏模型。

反演结果评价同样采用式(9)和式(10)模型开展,但是考虑到真实信号的模糊性,当信号样本属于较低SNR 条件(小于3 dB)时反演设定条件及相关评价准则放宽至目标反演偏差εT=0.03,其他不变;同时为了避免模型陷入单个参数采样的局部优化,在采样算法的步骤5)设定单参数最大无效反演5 轮次后,以新的随机参数向量重新开始反演。

4.3 模型参数反演

基于实际数据样本对无目标闪烁条件的水声往返双程信道时域起伏模型参数开展反演。设定σ2随机采样区间[0.1 1],K随机采样区间[0.5 3],反演最终结果如下。

4.3.1 不同SNR 信号反演

表1 不同SNR 信号参数反演结果对比Table 1 Comparison of parameter inversion results under different SNR signals

2 组反演结果对应的Ricean 分布PDF/CDF 与真值分布对比如图5 所示。

图5 不同SNR 信号反演结果与真值分布对比Fig.5 Comparison of inversion results with true distributions under different SNR signals

反演结果表明,SNR 水平对于反演结果影响较大: 在相同发射接收水平下,SNR 越高反映信道质量越好,代表直达信号强度的K因子越大,而表征多途信号功率的 σ2参数越小。此外,在较高SNR 条件下信号起伏分布规律与正演模型相似度更好,表现为用于评价PDF 整体差异的结果更小,表征分布相似性的KL 散度指标也更小。同时方差分析表明不同信号条件下,各评价参数均有较好的收敛一致性。最后,反演结果与真值的总体差异也表明所建立的水声双程信道仿真模型是有效的,尤其是在较高SNR 条件下。

4.3.2 多样本反演

文中最后选择了来自于某海域实航试验的9 组在时空上有一定联系的实际信号进行了模型参数反演。其中,前8 组数据信道传输距离自1 000～2 000 m 非等间隔分布,SNR 为1～2 dB,第9 组数据作为对照SNR 条件约3 dB,信号时域形态如图6 所示。

图6 多样本脉冲回波时域信号Fig.6 Multiple groups of pulse time domain echo

反演初始设定及过程参数与4.3.1 节相同,均进行100 趟反演。1～8 组反演结果对应的Ricean分布PDF/CDF 与真值分布对比如图7 所示。

1～8 组反演结果如表2 所示。

各参数的变化趋势如图8 所示。

作为对照,对第5、9 组数据按同样条件进行了100 趟反演,参数反演过程结果对比见图9。

第5、9 组信号参数反演结果的对比如表3所示。

表3 第5、9 组信号参数反演结果对比Table 3 Comparison of inversion results at 5th&9thgroups signals

第5、9 组反演结果对应的Ricean 分布PDF/CDF与真值分布对比如图10 所示,其中横纵坐标与前文定义相同。

针对上述反演统计结果的分析表明:

1)从表1 及图7 结果可知,各组反演过程均成功收敛,反演结果与真值误差按模型所定义的总体差异均在5%以内;

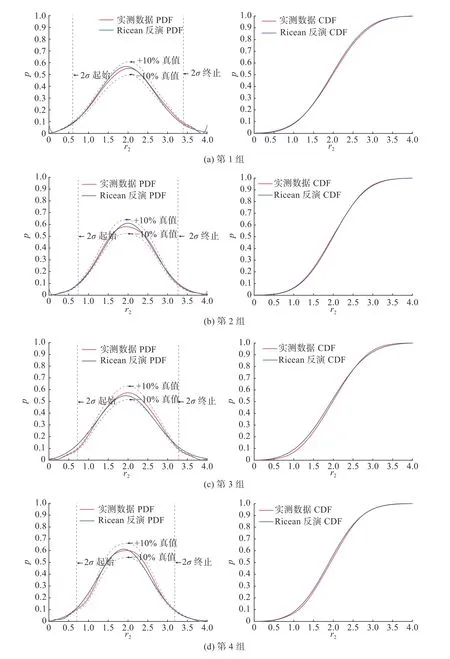
图7 1～8 组信号反演结果与真值分布对比Fig.7 Comparison of inversion results with true distributions at 1thto 8thgroups signals

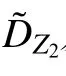
图8 1～8 组反演参数变化趋势Fig.8 Change trend of inversion parameters at 1thto 8thgroups signals

表2 1～8 组双程信道模型参数反演结果Table 2 Parameter inversion results of go-back channel model at 1thto 8thgroups signals

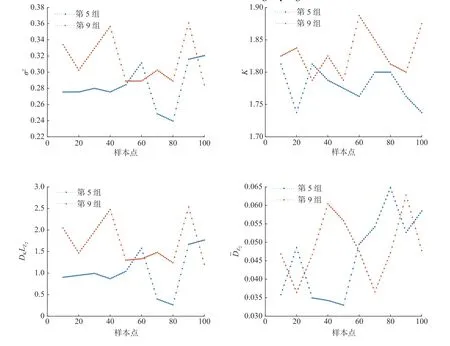
图9 第5、9 组双程信道模型参数反演过程结果对比Fig.9 Comparison of parameter inversion results of go-back channel model at 5th&9thgroups signals

图10 第5、9 组信号反演结果与真值分布对比Fig.10 Comparison of inversion results with true distributions at the 5th&9thgroups signals

5 结束语

针对水下作战装备研发对水声环境仿真需求,基于贝叶斯全概率公式构建了水下目标回波双程衰落信道模型,并结合针对实测时域数据的模型参数反演特点,设计了单维度串行采样模型。模型通过M-H 核函数设计,将MCMC 方法引入全局反演算法中,以有效利用有限实测数据信息,为水下目标回波仿真模型置信度提升提供了有力而灵活的保证。文中使用仿真双程信道数据对反演算法的有效性进行了验证,并在最后使用多组实测数据开展反演,通过对反演结果的分析确认了双程衰落信道模型的正确性。

值得注意的是,在使用实测数据开展模型参数反演时,除了信号SNR 条件会对反演效率和结果产生较大的影响外,准确的识别接收信号中脉冲回波所在空时区间是反演有效开展的重要保证,在算法的后续优化中,可针对实测数据的自动选取及预处理开展更多工作,以进一步提升反演速度和结果的准确性。