一种水声自适应通信的信噪比估计方法

王 巍 ,普湛清 ,钮 彪 ,陶 磊 ,黄海宁

(1.中国科学院 声学研究所,北京,100086;2.苏州桑泰海洋仪器研发有限责任公司,江苏 苏州,215000)

0 引言

随着我国海洋事业的持续发展,越来越多的水下潜标、水下机动无人平台投入到海洋监控、水下安保、矿产勘探等任务中。受电磁波水下传播能力弱的限制,水下各类型节点无法直接与水面无线网络直接进行信息交互,严重制约了水下观测监察网络整体效能。因此,如何高效、稳定地实现水下观测监察网络与水面网络间的信息跨介质交互和信息融合成为近年来研究的热点。目前,国内外针对跨介质数据传输方法的研究主要集中在通过声、光、电磁波等手段直接进行水下-水面信息交互[1-5]。文献[6]给出了采用中继浮标实现跨介质通信链路的思路,通过在跨介质浮标上搭载集成了水声通信和无线通信的终端设备实现水下-水面平台数据跨介质交互。该方案面临的难点之一是跨介质网关能耗过大的问题,该问题是由水下用户运动、海况复杂多变等因素作用导致的异构通信链路信道状态不稳定性所带来的。链路自适应通信技术[7]是解决这一问题的有效手段,已在无线电通信中得到了广泛的应用。链路自适应通信技术的应用前提是对通信链路信道状态的准确认知,信噪比(signal-to-noise ratio,SNR)估计技术是评估信道状态的重要手段,相关研究成果丰富[8-10]。文献[9]提出了采用导频辅助的最小均方误差(minimum meansquare error,MMSE)SNR 估计方法,通过利用前一时刻的信道估计结果均衡当前符号的导频数据,稳健实现了数字通信信号的SNR 估计。该方法要求信道在一定的时间内保持稳定,因此在信道时变性强的水声通信中应用时需要连续添加导频以实时跟踪信道变化,导致通信效率下降。文献[10]中给出了基于高阶累积量的二阶矩四阶矩(M2M4)全盲算法,该方法计算简单,同时对载波相位偏差不敏感,适合低SNR 条件下的水声通信信号处理。

为保障链路自适应跨介质通信的稳健性,链路数据率的调整通常采用在信道状态变差时,快速降低数据率,在信道状态转好时,稳健提升数据率的策略。链路自适应通信的SNR 估计方法应同时具备高SNR 条件下估计结果准确、低SNR 条件下估计结果对接收信号SNR 下降敏感的特征。因此,M2M4 在低SNR 条件下的稳健性不适合采用“快降慢升”策略的跨介质自适应通信链路。针对上述问题,提出了一种适合跨介质自适应通信的SNR 估计方法,该方法以导频辅助的MMSE 信噪比估计方法为基础,结合文献[11]中的低导频占用率信道估计技术增加SNR 估计有效数据量,将维特比译码的误码扩散特点与文献[12]所提判决反馈方法结合,实现了通信链路在高SNR 条件下的高精度SNR 估计,以及低SNR 条件下的SNR 估计值快速降低的信道状态估计方法。

1 改进的MMSE 信噪比估计算法

1.1 MMSE 信噪比估计算法

MMSE 信噪比估计算法是一种基于导频或数据判决的估计算法,以均方误差的代价函数最小为准则。假设发送端待发送数据为D,经过信道编码和相位映射后,调制到M个由J 个子载波构成的正交频分复用(orthogonal frequency division multiplexing,OFDM)符号上,得到待传输数据矩阵X={X1,X2,···,Xm,···,XM},其中Xm={Xm={xm,1,xm,2,···,xm,j,···,xm,J}。

假设传输第m个OFDM 符号时,信道频域响应向量为Hm={hm,1,hm,2,···,hm,j,···,hm,J},hm,j为第m个OFDM 符号传输时,第j个子载波传输信道的频域响应。第m个OFDM 符号到达接收端的数据Ym={ym,1,ym,2,···,ym,j,···,ym,J}可表示为

其中,Δm={σm,1,σm,2,···,σm,j,···,σm,J}为第m个OFDM 符号传输时的加性噪声向量。

根据文献[11],MMSE 信噪比估计算法表示为

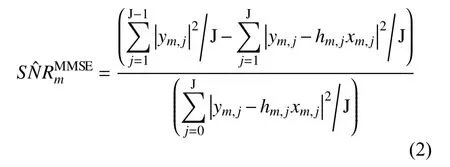
1.2 改进的MMSE 信噪比估计算法

MMSE 信噪比估计算法在低SNR 环境下依然可以稳健、准确估计接收信号的SNR,在数字通信中应用广泛。由式(2)可知,MMSE 信噪比估计算法取得较好估计结果的前提是对信道的准确估计。由于布放于海面的跨介质通信浮标受到海流、海风、涌浪、云层和降雨等因素干扰,异构跨介质通信链路信道状态时变性较强,因此需要添加大量的导频信息用以重建和追踪信道的变化,导致通信效率降低。

针对上述问题,文中提出了一种改进的MMSE信噪比估计方案。改进的算法利用低导频占用率信道估计过程中的重构数据进行SNR 估计,在不显著增加计算量的基础上,完成对时变信道的实时追踪与接收信号SNR 估计。与MMSE 信噪比估计算法相比,所提的改进SNR 估计方法可以在添加少量导频的基础上,提高在高SNR 接收条件下的SNR 估计结果准确度,同时在低SNR 接收条件下改进算法的估计结果能够快速下降。

低导频占用率信道估计算法在匹配追踪(matching pursuit,MP)算法和最小二乘(least square,LS)信道估计算法之间构建迭代回路,抑制了基于符号判决的OFDM 均衡算法存在误码遗传的问题。

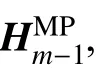
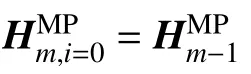
式中,加权向量Wm包含字典Ψ 内所有原子的加权系数,当且仅当l∈Sm时取值非0(或远大于0)。

8)重复步骤1)～8),直到满足迭代终止条件或达到最大迭代次数I。

9)当i＜I时,令i=I,将代入式(2)得到改进的MMSE 信噪比估计值

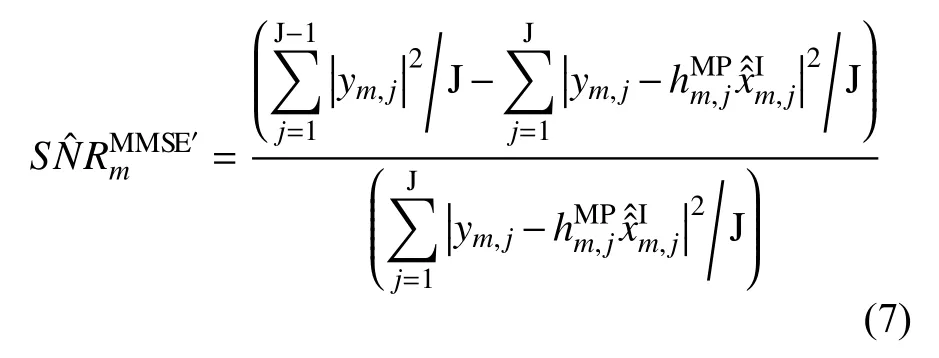
其中:为第m个OFDM 符号的第j个子载波信道的第I 次迭代、或达到信道估计最大迭代终止条件时的信道估计响应值;为第m个OFDM 符号的第j个子载波信道的第I 次迭代重建的子载波相位。

1.3 改进算法性能分析

相较MMSE 信噪比估计算法,文中提出的改进方案更加适合时变性较强的跨介质异构链路自适应数据调整策略。

由于改进的MMSE 信噪比估计算法利用了低导频占用率信道估计技术中间过程的数据,受益于低导频占用率信道估计技术,改进算法需要的冗余导频数量相较于原始算法显著降低,提升了通信系统整体的通信效率。

为验证改进的MMSE 信噪比估计算法的可行性和可靠性,通过Matlab 软件对算法进行仿真。表1 给出了OFDM 通信系统仿真采用的主要参数。系统采用的卷积码(convolutional code,CC)每次编码长度与单个OFDM 符号的实际可载信息量一致。4 个OFDM 符号构成1 帧通信脉冲。

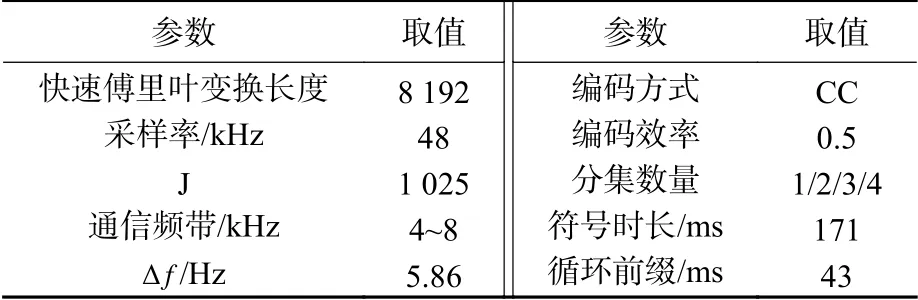
表1 OFDM 系统主要参数Table 1 Main parameters of OFDM system

图1 给出了由某信道仿真软件生成的浅海信道冲激响应模型以及利用低导频占用率信道估计算法匹配出的信道结果。发射换能器和接收水听器均布放在水下10 m 处。发射端与接收端水平相距5 m,平均海深60 m。对比原始信道和匹配出的信道结果可以发现,MP 算法在43 ms 时延范围内,对信道主要抽头的幅值和时延都能较为准确地估计。而43 ms 时延以外的抽头由于受到MP 算法时延估计能力的限制而无法重构,被当作噪声处理。

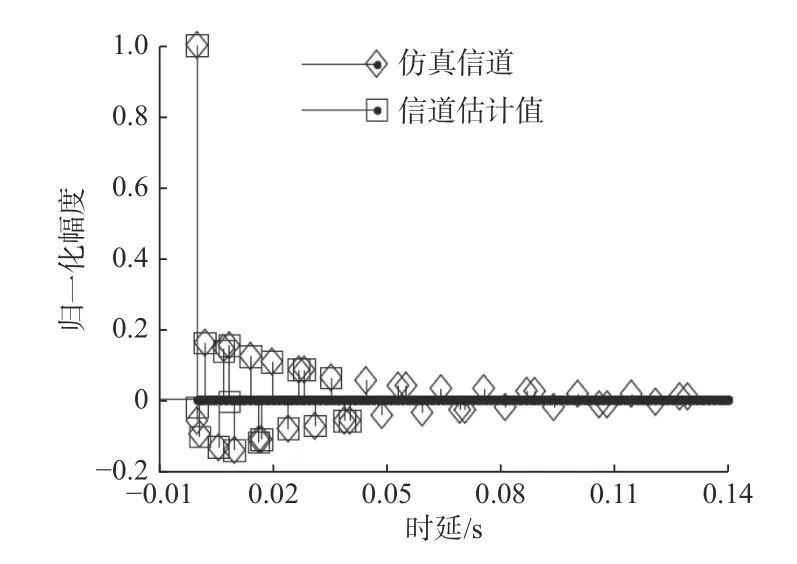
图1 仿真信道冲激响应与其估计结果Fig.1 Simulation channel impulse response and its estimation results

在图1 所示的信道条件下仿真对比所提SNR估计算法性能。图2 给出了SNR 添加条件下的MMSE、改进MMSE 以及M2M4 信噪比估计算法的估计效果对比。通信系统仿真参数(见表1),其中数据未采用频域分集。MMSE 信噪比估计算法在每个OFDM 符号中等间隔插入梳状导频,导频间隔为3,因此其导频占用率为25%。改进的MMSE 信噪比估计算法仅在第1 个OFDM 符号中随机选取128 个子载波作为导频。由于每个符号包含1 025 个子载波,因此该导频占用率为128/(1 025×4)=3.12%。

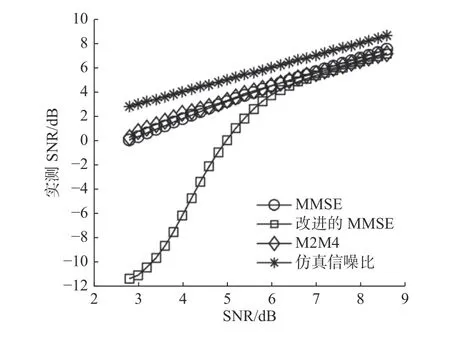
图2 相同信噪比条件下不同信噪比估计方法输出结果Fig.2 Output results of different SNR estimation methods under the same SNR condition

由图2 可知,MMSE 信噪比估计算法和M2M4信噪比估计算法性能接近,而改进的MMSE 算法在6 dB 以上仿真条件下SNR 估计结果与对比算法性能几乎一致,在6 dB 以下仿真条件,SNR 估计结果相较对比算法快速下降。此外,3 种SNR估计算法的估计结果在高SNR 条件下与真实添加SNR 有约1 dB 的偏差,这一误差来源于低导频占用率信道估计的重构残余和信号带通滤波的共同影响。

图3 为利用图2 仿真数据在相同原始误码率条件下,不同SNR 估计算法的输出结果对比。不难发现,当原始误码率低于2%时,改进算法与对比算法性能相似;当原始误码率高于2%时,改进算法输出衰减速率显著高于对比算法和真实仿真。

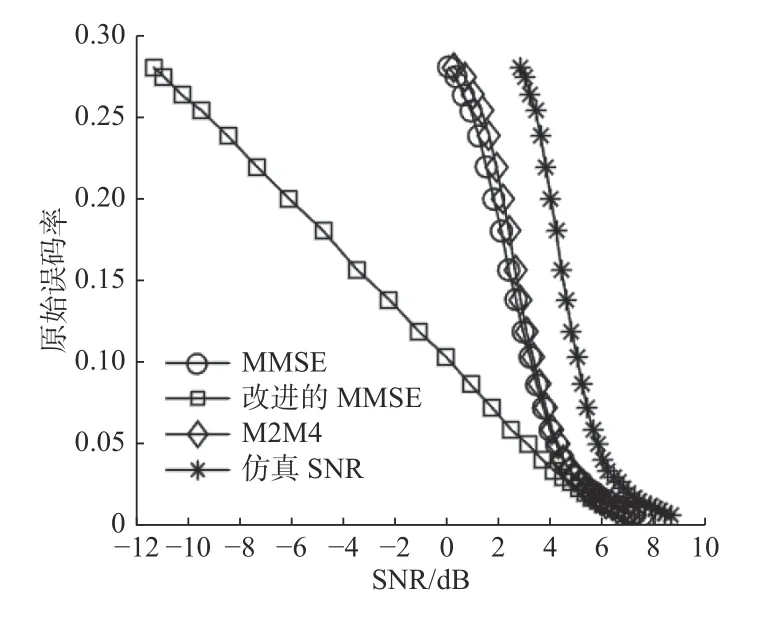
图3 相同原始误码率条件下不同信噪比估计算法输出结果对比Fig.3 Comparison of output results of different SNR estimation algorithms under the same original bit error rate

图4 给出了在不同分集数量的条件下,改进MMSE 信噪比估计算法与M2M4 信噪比估计算法的性能仿真对比。仿真中数据分集方法采用频域分集,分集数量分别为2、3 和4,对应的通信数据率为533、712 和1 066 bit/s。分集数据在解码前,采用最大比合并算法进行数据合并。可以看到,经过分集合并后,在相同的误码平层下,接收信号利用M2M4 算法测得的SNR 数据结果接近,而采用改进的MMSE 算法则显著放大了输出SNR 差异,使得链路在低SNR 环境下对信道状态变化更为敏感,有利于链路自适应通信策略的实现。

图4 不同分集数量条件下不同信噪比估计算法输出结果Fig.4 Output results of different SNR estimation algorithms under the different sets quantity

表2 为根据图4 设计的链路自适应数据率调整门限,采用的数据率调增策略为连续2 次高于调增门限(图2 中仿真误码率小于2%),调减策略为连续3 次低于调减门限(图4 中仿真误码率高于4%)。

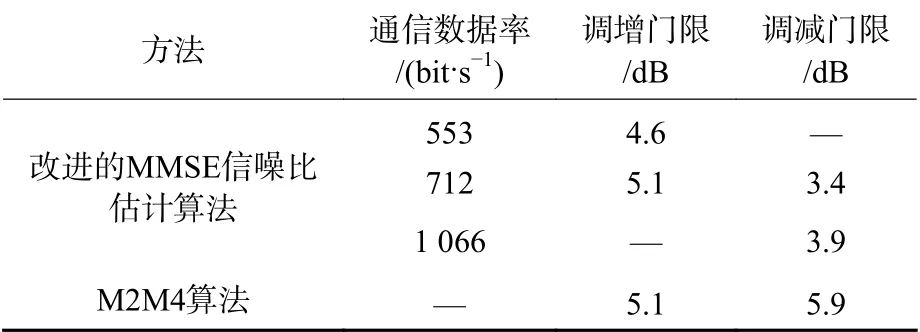
表2 通信数据率调整策略Table 2 Communication data rate adjustment strategy

利用改进的MMSE 信噪比估计算法和M2M4信噪比估计算法结果,依据表2 数据率调整策略,进行数据率变化仿真,仿真轮次共计900 轮,图5(a)和图5(b)给出了采用改进的MMSE 算法与M2M4算法前120 轮次仿真结果。表3 中给出了2 种算法在900 轮次仿真试验平均数据率、误码率以及数据切换次数的统计结果。

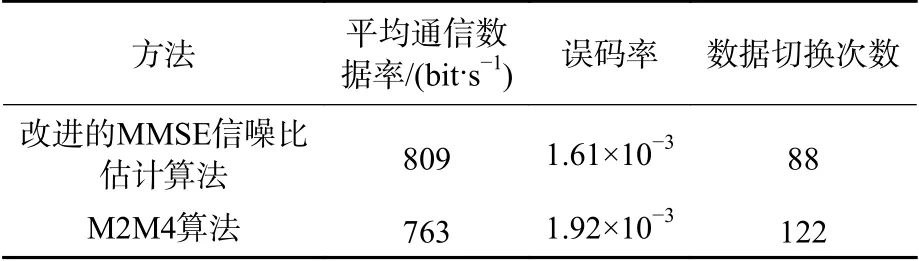
表3 不同算法性能对比Table 3 Performance comparison of different algorithms

由图5(a)可知,根据表2 中改进的MMSE 信噪比估计算法给出的自适应策略,仿真通信数据率变化与SNR 变化走势一致。在900 轮次的仿真试验中,链路自适应通信平均数据率为809 bit/s,平均误码率为1.61×10-3,数据率切换次数为88 次。

图5 不同链路自适应策略下通信数据率变化对比Fig.5 Comparison of communication data rate changes under different link adaptive strategies

由图5(b)可知,根据表2 中M2M4 信噪比估计算法给出的自适应策略,仿真通信数据率变化与SNR 变化走势一致。在900 轮次的仿真试验中,链路自适应通信平均数据率为763 bit/s,平均误码率为1.92×10-3,数据率切换次数为122 次。

通过对比图5(a)和图5(b)可以发现,与M2M4算法相比,在改进的MMSE 算法给出的链路自适应策略下,数据切换次数减少30%,更少的数据率切换次数可以减少接收端发送信道状态信息(channel state information,CSI)反馈信号次数,降低接收端的发射功耗,通信链路平均数据率提高了6.03%。

由图6 可知,改进MMSE 信噪比估计算法与M2M4 对比算法对SNR 测算结果随通信轮次的变化趋势与实际仿真添加SNR 的变化趋势一致,由于2 种算法估计得到的SNR 为数据分集合并后的输出结果,因此2 种算法测量值均比仿真值偏高。

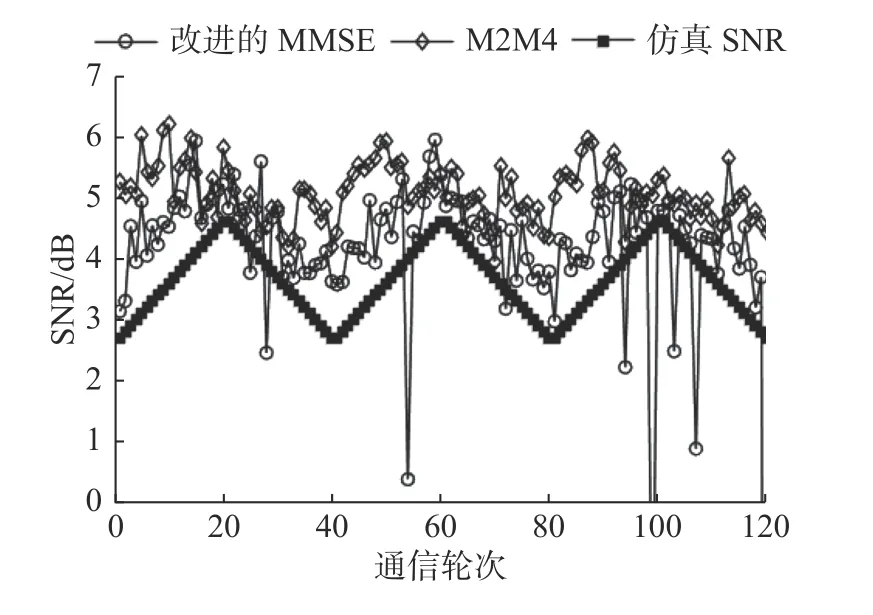
图6 不同轮次信噪比测算结果Fig.6 SNR measurement results of different rounds

2 结束语

文中研究了跨介质异构通信网络链路自适应技术中的SNR 估计问题,提出了一种改进的MMSE 信噪比估计方法。该方法结合具有高通信效率的低导频占用率水声信道估计算法,利用信道估计过程中的重构数据对传统MMSE 信噪比估计方法进行改进,提高时变信道条件下的SNR 的估计精度和实时跟踪性能。仿真试验结果表明,改进算法在高SNR 条件下具备足够的SNR 估计精度,在低SNR 条件下的SNR 估计结果衰减速度相较于对比算法显著提高,因此改进算法的SNR估计结果更适合作为跨介质链路自适应速率调整策略的依据。链路自适应通信的仿真试验结果表明,与对比方法相比,改进的MMSE 信噪比估计算法给出的自适应策略具有更少的通信速率切换次数,降低了发射功耗,显著提高了误码性能和通信平均数据率。