面向小型水下无人平台的移动水声通信系统

姚俊辉 ,赵燕锋 ,童 峰* ,陈东升 ,上官明禹

(1.厦门大学 海洋与地球学院,福建 厦门,361005;2.厦门大学 导航与位置服务技术国家地方联合工程研究中心,福建 厦门,361005;3.厦门大学 人工智能研究院,福建 厦门,361005;4.福州大禹电子科技有限公司,福建 福州,350001)

0 引言

近年来,具有目标特性小、成本低、部署方便等突出特点的各类小型化自主水下航行器(autonomous undersea vehicle,AUV)在水下特战领域的应用得到国内外广泛重视[1]。移动水声通信作为AUV 等水下无人平台的主要通信方式,在水下无人平台指挥控制和信息回传等环节中发挥着至关重要的作用。

然而,水声信道高时变的多径效应和多普勒效应严重影响了通信链路的稳定性与通信质量的可靠性[2],特别是对于水下特战领域小型水下无人平台,在多样化任务下,运动状态变化大、浅海应用多、受限功耗下发射功率低,因此,如何高效地克服由此造成的多径严重、多普勒快速多变、接收信噪比低等困难成为该领域小型水下无人平台移动水声通信亟待解决的关键问题。

国内外对移动水声通信中多普勒估计与补偿问题的研究发展已久。Sharif[3]、Zakharov[4-5]等分别提出多普勒估计法[3],以及搜索最大互相关峰值多普勒估计方法[4]和分步式多普勒估计方法[5];周成阳等[6]提出了基于数据样本方差的多普勒估计方法;Li 等[7]提出了互相关准梯度的多普勒估计算法,其通过不同补偿因子下匹配滤波器输出峰值的变化梯度来调整搜索步长的方法来降低算法的计算量。

在上述文献中,获得多普勒估计结果后均采用时域插值方法进行多普勒补偿,通过插值实现重采样的多普勒补偿方法缺乏实时性且补偿精度较低,无法满足对失真要求较为严格的系统;同时,重采样方法在实时处理中对存储量和算力要求均较高。

张晓[8]通过基于Chip-Z 变换的伪随机序列载波频偏测量的估计多普勒,同时采用了基于Farrow结构滤波器的多普勒补偿方法,这种利用数字滤波器进行采样率转换实现重采样的多普勒补偿方法具有较高的重采样精度,但仍有占用硬件内存大和实时性差的缺点。

在多普勒补偿低复杂度硬件实现方面,王小阳等[9]提出了一种可用于低复杂度硬件的多普勒补偿方案。该方案利用线性调频(linear frequency modulation,LFM)前导序列进行多普勒频移的估计,并根据估计结果基于处理器时基实时调整AD(Analog-to-Digital)芯片的采样率来实现多普勒补偿。该方案将多普勒估计与补偿环节提前,可实时实现多普勒的估计与补偿。但由于该方案中基于处理器时基提供的AD 芯片采样率调整范围有限,在面对大尺度多普勒影响时该方案无法提供对应的采样率来实现硬件补偿。此外,该方案多普勒补偿的精度也受限于AD 芯片中采样率的分辨率。

面向小型水下无人平台的应用场景,结合直接序列扩频-四相差分相移键控调制方式(direct sequence-quadrature differential phase shift keying,DSQDPSK)和差分编码方式,并引入直接数字频率合成器(direct digital frequency synthesizers,DDS)为硬件系统提供大范围和高分辨率的采样率,提出了一种基于DDS 变采样的移动水声通信方案。利用双曲调频(hyperbolic frequency-modulation,HFM)导引信号对多径信道中的最强径进行多普勒估计,采用的差分编码方式为系统提供了一定的多普勒容限,可弥补低估计精度的缺陷。文中采用DDS变采样的方法进行多普勒补偿,相对于重采样的多普勒补偿方法,硬件变采样补偿的优势在于可实现信号采集与多普勒补偿同步进行,无需重构信号,实时性高。此外,DDS 提供的高精度分频也使系统具备较高的补偿精度。半实物仿真实验结果表明了文中所提方案的有效性。

1 系统设计

1.1 DS-QDPSK 调制方式

采用的DS-QDPSK 调制方式中,直接序列扩频的调制方式具有强抗干扰能力和低检测阈的优势[10]。扩频通信系统扩展的频带越宽,在同等量级噪声干扰时落入信息带宽内的干扰信号强度则会越小,其抗干扰能力因此越强。不仅如此,由于扩频通信系统的信号频谱被扩展,扩频系统也具有一定的抗频率选择性衰落的能力。

考虑到LFM 信号在强多普勒效应的影响下会存在与本地同步信号失配的情况,造成匹配滤波器输出的相关峰出现峰值下降甚至发生分裂的现象,文中采用了具备多普勒不变性的HFM 信号作为导引信号及同步信号[11]。文中系统发射信号帧格式如图1 所示,信号帧由导引信号、同步和信息序列三部分组成。导引信号部分包含了若干个HFM 信号,以有效防止误同步发生,确保接收信号同步捕获的稳定性;同步部分为1 个HFM 信号,作为探针确定信息序列起始位置。信号调制所用载波的中心频率为25 kHz,带宽为5 kHz,采样率为75 kHz。

图1 发射信号帧格式Fig.1 Frame format of transmit signal

DS-QDPSK 调制解调的系统流程如图2 所示。首先,将信源的原始二进制信息序列先后进行卷积编码、交织以及差分编码;随后将编码后的二进制信息转化为四进制;伪随机码(pseudorandom noise,PN)发生器生成4 种不同的PN 序列,分别对应四进制中的0～3;最后,将四进制信息映射成对应的PN 序列,实现DS-QDPSK的多进制扩频信息调制。

图2 DS-QDPSK 系统流程Fig.2 System process of DS-QDPSK

在接收端,定位到接收信号信息序列位置后将之与本地PN 码做相关,用非相干解调的方式进行解扩。随后将解得的原始信息序列依次进行解差分、解交织和卷积译码,最终得到解调信息。

1.2 双曲调频信号

文中导引序列采用HFM 信号,其时域表达式为

其中

式中:fh和fl分别为HFM 信号频率的上下边界T为HFM 信号的持续时间,因此t0和K均为常数。HFM 信号的瞬时频率可用其相位对t求导后除以2 π来计算[12],即;

从HFM 信号瞬时频率的表达式中可以看出其是一个双曲函数。HFM 信号的频谱图如图3所示。

图3 HFM 信号时频图Fig.3 Time-frequency diagram of HFM signal

设多普勒因子为 α,则其接收信号的时域表达式可以表示为

则其瞬时频率为

与式(3)对比,可看出接收信号与发射信号的瞬时频率之间的关系为

从上式可以看出,多普勒频移后的HFM 信号的瞬时频率相对于原信号只是在时域上有一个固定的偏移。这说明对HFM 信号而言,多普勒效应只改变了接收端相关器输出峰值的位置,且峰值位置的偏移与多普勒因子之间存在特定的解析关系。所以,HFM 信号具有多普勒不变性的优势。

1.3 多普勒估计与补偿

1)多普勒估计

文中系统利用前导序列中的若干个导引信号做多普勒估计。在接收端,用本地同步信号与导引信号做相关,寻找最强径所对应的相关峰位置,计算首尾相关峰之间的时间差即为接收信号首、尾导引信号间隔的时长,并结合原始信号中其间隔时长可估计出多普勒因子为

式中:Toriginal为原始信号首、尾信号间隔的时长;Trecieve为接收信号首、尾导引信号间隔的时长。

文中采用的多普勒估计算法的精度取决于导引信号的长度。信号帧的导引信号中,每个HFM信号长度为1 700 个采样点(约22.7 ms),采样间隔长度为348 个采样点(约4.6 ms),用于多普勒估计的导引信号长度为18 432 个采样点(约245.8 ms)。因此在多普勒估计过程中,对接收端导引信号的时长测量每偏差一个采样点,得到的多普勒因子则会相差1/18 432,结合信号中心频率(25 kHz)换算成多普勒频移约为1.36 Hz,即文中多普勒估计算法的分辨率约为1.36 Hz。因此,按分辨率的一半粗略估计,文中多普勒估计算法的估计精度在0.68 Hz 左右。

2)多普勒补偿

由于多普勒效应的影响,接收端信号会被压缩(fd为正时)或扩展(fd为负时),接收信号的中心频率变为(fc+fd)。在接收信号长度压缩(或扩展)的情况下,若仍以发射采样率fs对接收信号进行采样,采集到接收信号的采样点则会相对发射信号出现偏差,导致解调误码情况恶化。因此,若要还原原始信号的采样点位置,可调整接收采样率为

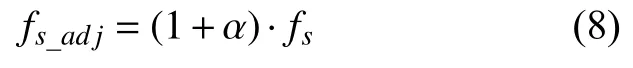
2 硬件设计

文中系统硬件基于STM32F407 核心处理单元以及DDS 变采样模块实现。具体地,采用DDS 芯片AD9954 来产生STM32F407 的外部时钟信号,采样率fs与外部时钟信号I2S_CLK的关系可以表示为

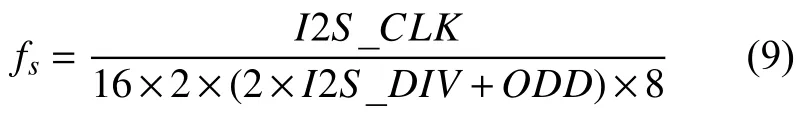
式中:I2S_CLK为外部时钟的时钟频率;16 表示通道帧宽度为16 位;I2SDIV为I2S线性预分频器的值,其取值范围为2～255;ODD代表预分频器的奇数因子,其取值为0 或1。根据上式可通过调整I2S_CLK、I2SDIV以及ODD的取值来实现采样率的实时调整,文中为了使采样率可调的取值范围尽可能大,固定取I2SDIV=2,ODD=0,由此,式(9)中fs的表达式可简化为

式中,I2S_CLK取值为正整数,所以由上式可得DDS 的分频精度可达到10-3Hz。因此,DDS 变采样方法的补偿精度约在10-4Hz 的数量级。软件重采样多普勒补偿的方法需通过对采样点数做近似处理来保证重采后信号的采样点数为整数。经计算,若以软件重采样的方法对文中信号做多普勒补偿,其产生的补偿误差约在10-2Hz 的数量级。由此可见,所采用的DDS 变采样在多普勒补偿精度方面优于软件重采样。

多普勒估计与补偿的流程如图4 所示,接收端换能器上传的接收信号在经过前置滤波放大电路后进入STM32F407 核心处理单元中,核心处理单元中的WM8978 芯片以75 k 的初始采样率(即发射采样率)完成对接收信号导引信号部分的数字信号采集,在定位到导引信号时,根据式(7)估计出多普勒因子,并根据式(8)计算出所需调整的采样率;然后,核心处理单元通过串口发送相应的调频指令给DDS 变采样模块,DDS 则会反馈相应频率的外部时钟信号给核心处理单元,WM8978 芯片在此外部时钟信号的控制下以调整后的采样率对信号的剩余部分进行采样并解调,由此实现了基于DDS 变采样的多普勒补偿。

图4 多普勒估计与补偿流程Fig.4 Doppler estimation and compensation process

3 半实物仿真实验

3.1 浅海信道模型

为了方便以半实物仿真的方式评估文中系统在浅海水声信道下的抗多普勒能力,以厦门港海域实测参数为参考,综合多径效应,多普勒频移以及噪声干扰的影响,设计了如图5 所示的仿真水声信道模型。

图5 水声信道仿真模型Fig.5 Simulation model of underwater acoustic channel

水声多径信道由BELLHOP 得到,如图6 所示。该信道的声速剖面数据来源于厦门港的声速仪实测数据,声速在1 514～1 515 m/s 的范围内呈现一个微弱的正梯度。设海水深度为25 m,发射端与接收端相距1 km,收发换能器入水深度均为3 m。仿真多径信道的单位冲激响应如图7 所示,可以看出,该信道有10 条到达径,最大时延约为8 ms。

图6 BELLHOP 多径信道仿真Fig.6 Multipath channel simulation of BELLHOP

图7 信道单位冲激响应Fig.7 Impulse response of channel

3.2 半实物仿真实验流程

半实物仿真实验的流程如图8 所示。1)将调制的发射信号输入仿真水声信道模型中生成该信道下的接收信号;2)用NI-DAQ 数模转换模块将接收信号转换为模拟信号;3)将生成的接收信号输至STM32F407 核心处理单元中,进行多普勒估计和补偿以及硬件解调;4)通过串口在上位机界面显示解调结果并进行误码率的计算和实验结果的分析。

图8 半实物仿真实验流程Fig.8 Flow of hardware-in-the-loop simulation experiment

3.3 半实物仿真实验结果

为了评估系统在不同尺度多普勒频移影响下的工作性能,实验通过对发射信号进行软件重采样的方法分别引入了10,20,30,40 和50 Hz 的多普勒频移(依次对应1.2,2.4,3.6,4.8 和6 kn 航速下的多普勒频移)。最后,叠加-8∶4∶20 dB 信噪比的带内噪声来模拟水声信道中环境噪声对系统性能的影响。

图9 为在不同信噪比条件下,硬件对人工引入不同尺度多普勒频移信号的多普勒估计结果。可以看出,当信噪比大于0 dB 时,各尺度多普勒估计值分别为50.18,40.69,29.84,20.35 和10.85 Hz,均达到了当前估计精度下最精准的结果;在信噪比低于0 dB 时,除了10 Hz 和20 Hz 中多普勒估计结果出现了少许的误差之外(-4 和0 dB 时10 Hz的多普勒估计结果为13.56 Hz,-4 dB 时20 Hz 的多普勒估计结果为18.99 Hz),其他尺度多普勒的估计值仍取得了理想的结果。

图9 多普勒估计结果Fig.9 Doppler estimation results

需要指出,10 Hz 和20 Hz 在低信噪比条件下多普勒估计中出现的误差可能是以下2 个因素共同作用的结果。首先,实验中通过软件重采样来仿真多普勒频移,由于重采样后信号的采样点数需为整数,因此在重采样过程中做了近似处理,其中引入10 Hz 和20 Hz 多普勒的过程中存在相对更大的误差;其次,硬件信号采集的过程中也会存在系统误差,无法做到与原信号采样值完全一致,尤其在低信噪比的情况下由此产生估计误差的可能性更大。

图10 为半实物仿真的误比特率(bit error rate,BER)结果。可以看出,在不同尺度多普勒频移影响下的误码率曲线均随信噪比的增强而逐渐下降。在0 dB 信噪比时,50 Hz 以内各尺度多普勒仿真信号的解调误码率均达到了10-2量级及以下;在4 dB 信噪比时,误码率均降至10-3量级及以下;在信噪比大于4 dB时,基本实现了零误码。总体而言,文中提出的基于DDS 变采样的多普勒补偿方案在半实物仿真实验中取得了较为理想的结果,在中高信噪比和一定范围多普勒的条件下可满足水下移动平台之间的稳定通信。

图10 半实物仿真误比特率结果Fig.10 Bit error rate results of hardware-in-the-loop simulation

4 结束语

针对水下特战领域小型水下无人平台移动水声通信中强多径、快变多普勒及低信噪比对可靠水声通信造成的挑战,结合HFM 前导序列、直接扩频序列调制和差分编码等方式,采用基于DDS变采样的多普勒补偿方案,该方案在低复杂度硬件实现的同时,可实现实时多普勒估计与补偿的功能。

半实物仿真结果表明,在较低信噪比以及多径条件下,文中提出的基于DDS 变采样的多普勒补偿方案可实现对多普勒频移的精准估计,有效改善了50 Hz 以内多普勒影响下的系统通信性能,可保障6 kn 以内航速的水下移动平台与控制基站之间的稳定通信。需要指出,文中所提多普勒补偿方案现阶段针对信号帧范围内进行整体的多普勒估计与补偿,在后续工作中将对帧内小范围精细多普勒估计与补偿开展进一步的研究。