短悬臂盖梁柔性拉压杆模型分析研究
黄 华
(中国市政工程中南设计研究总院有限公司,湖北 武汉 430010)
0 引 言
自20世纪80年代以来,国际工程界倡导将混凝土结构划分为B区和D区。B区是指截面应力分布符合平截面假定的区域,可按常规计算方法分析;而D区又称为应力扰动区,指截面应变分布不符合平截面假定的构件或力流扩散明显的区域,一般位于集中力作用点附近或几何尺寸突变处[1]。
混凝土桥梁中常见的应力扰动区有桩基承台、短悬臂盖梁(花瓶墩)、牛腿等,对于应力扰动区常见的分析方法有拉压杆模型方法和实体有限元模型方法。拉压杆模型是从连续的混凝土结构体内抽象出的一种简化力流分析模型,把结构离散成了只受拉拉杆、只受压压杆以及节点组成的桁架模型来分析结构的强度并进行配筋设计。实践表明,将拉压杆模型应用于结构D区的计算具有相当好的工程精度[2-3],不仅思路清晰,计算也十分方便。
《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)基于应力扰动区(D区)拉压杆模型给出了短悬臂盖梁承载能力极限状态的计算方法,但对于构件正常使用极限状态抗裂验算却未进行规定[4]。《混凝土结构设计规范》(GB 50010—2010)附录G中给出了深弯构件承载力的计算方法,同样没有对抗裂验算做出规定[5]。而《水工混凝土结构设计规范》(SL 191—2008)对于非杆件体系钢筋混凝土结构的裂缝宽度控制仅做出了限制钢筋应力的规定,根据环境类别的不同,对钢筋应力要求限制在0.5~0.7倍的抗拉强度标准值[6]。
如果直接按规范的拉压杆模型方法对钢筋应力进行抗裂验算,发现往往是抗裂计算控制配筋,即得出按规范拉压杆模型计算承载力来进行设计配筋不安全的结论。
分析可知,规范采用的拉压杆模型是基于刚性拉杆和刚性压杆节点平衡进行计算,而实际上,拉杆和压杆刚度一般相差较大,因此按刚性拉压杆模型计算可能会估高拉杆力,而考虑拉、压杆刚度差异的柔性拉压杆模型则更符合实际情况。
1 柔性拉压杆模型拉杆力的推导
建立短悬臂盖梁的简化模型来分析柔性拉压杆模型与规范计算方法的差异。图1为刚性拉压杆简化模型(规范推荐的拉压杆模型),图2则为考虑了拉杆、压杆刚度差异的柔性拉压杆简化模型。

图1 刚性拉压杆模型

图2 柔性拉压杆模型
1.1 刚性拉杆力计算
如图1所示,根据刚性拉压杆模型节点力的平衡可以得出:

式中:N为节点反力;Ns为拉杆拉力;Nc为压杆压力;θ为拉杆与压杆夹角。
1.2 柔性拉杆力计算
如图2所示,根据平衡条件,柔性拉杆变位与压杆变位存在如下关系:

此时,拉杆拉力为:

取压杆作为隔离体,压杆在节点反力N和拉杆拉力Ns'作用下的变位为:
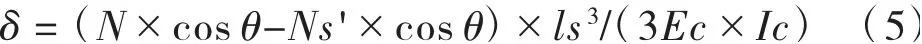
联立式(3)、(4)、(5)可求得拉杆拉力Ns',其值为:

将式(6)÷式(1),可以得到:

式中:δs为拉杆钢筋变位值;δ为压杆变位值;Ns'为柔性拉杆拉力;Ec为混凝土压杆弹性模量;Es为拉杆钢筋弹性模量;Ac为混凝土压杆面积,Ac=B×hc;As为拉杆钢筋面积;B,hc,lc为混凝土压杆宽度,高度及长度;ls为拉杆钢筋有效锚固长度;Ic为混凝土压杆惯性矩Ic=B×hc3/12。
式(6)给出了柔性拉杆力的理论计算公式。分析式(7)可知,柔性拉压杆模型计算得到的拉杆力实际要小于刚性拉压杆模型计算的拉杆力,其差异大小取决于拉、压杆的几何尺寸以及拉、压杆刚度比。
而工程设计一般是在结构尺寸拟定的基础上进行的结构受力配筋计算,故拉、压杆刚度比对拉杆力起到的了主导作用,其规律为拉、压杆刚度比越小,柔性拉杆力计算值越小,反之亦然。
2 柔性拉压杆模型有限元模型的验证
为验证柔性拉压杆模型计算分析的可靠性,结合一个工程实例通过三维实体有限元模型来进行对比验证。
2.1 工程概况
某实际工程项目,上部为现浇预应力混凝土箱梁,下部采用花瓶墩、桩基础。桥墩的主要结构尺寸如图3。桥墩采用C40混凝土,根据上部结构计算的结果,支座处反力极限组合为6 500 kN,频遇组合为5 000 kN。
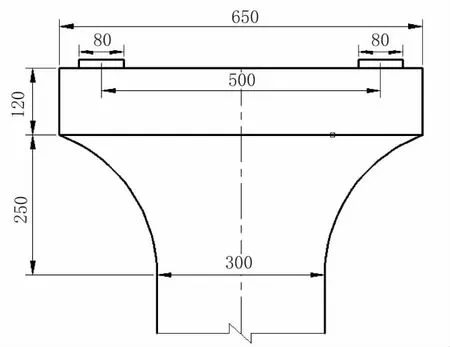
图3 桥墩尺寸(单位:cm)
根据规范计算拉、压杆夹角θ为48.5°,得到极限组合下拉杆拉力为5 754.6 kN,拉杆实配筋HRB400钢筋32根ϕ32,拉杆抗拉承载力为8 492.9 kN,故满足规范要求。
根据规范计算得到的频遇组合下的拉杆拉力为4 426.6 kN,拉杆钢筋应力为172 MPa,混凝土裂缝超限,尚需要增加钢筋。
2.2 柔性拉杆力计算
根据前述柔性拉压杆模型的理论推导公式计算拉杆拉力。其中,混凝土压杆弹模32 500 MPa,钢筋弹模200 000 MPa,拉、压杆夹角θ为48.5°,压杆斜长2 640 mm,压杆计算高度793 mm,由公式(6)、(7)可以得到:
极限组合反力下,柔性拉杆力Ne'为5 224.1 kN;频遇组合反力下,柔性拉杆力Ne'为4 018.5 kN,频遇组合下,拉杆钢筋应力为156 MPa,混凝土抗裂满足规范要求。
本例拉杆、压杆刚度比为15.4%,柔性拉杆力计算值约为刚性拉杆力90.8%。
2.3 实体有限元分析
为验证柔性拉压杆模型计算的可靠性,采用大型有限元程序MIDAS Fea建立了花瓶墩实体有限元模型,混凝土泊松比取用0.2,支反力以面荷载作用在垫石上,桥墩边界条件采用在墩底固结。
桥墩有限元实体模型如图4所示,在频遇组合反力作用下的横桥向拉应力云图及主应力云图如图5及图6所示。

图4 有限元实体模型

图5 横桥向拉应力云图
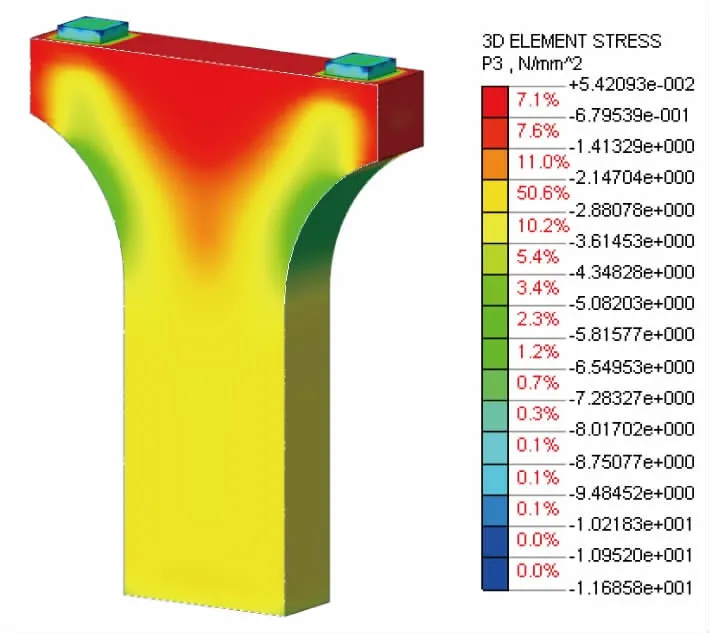
图6 横桥向主应力云图
通过对截面拉应力积分可以得到墩顶拉力合力值[7],计算得到拉力为3 596 kN。柔性拉压杆模型计算得到的拉杆拉力4 018.5 kN,与实体有限元模型计算值更为接近。
进一步分析,从主应力云图可以看出规范规定的压杆方向与主应力方向并不完全一致,当采用主应力方向作为压杆方向时,拉、压杆夹角θ修正为51.2°,重新代入公式(6)中可以计算得到柔性拉杆力为3692.8kN,与实体有限元模型的计算值的误差仅为2.7%。
以上分析证明柔性拉压杆模型的计算精度更高,柔性拉压杆模型与实体有限元模型的计算结果更为接近,且偏于安全。
2.4 拉、压杆刚度比对拉杆力的影响
通过调整拉、压杆的刚度比,可以得到不同的拉杆力之比(柔性/刚性)的变化规律,同时,也可以得到不同的压杆力之比(柔性/刚性)的变化规律,如图7所示。

图7 拉压杆受力与刚度的关系
由图7可知,当拉、压杆刚度比小于2%时,柔性拉杆力折减为刚性拉杆力的80%以下;当拉、压杆刚度比介于5%~20%时(工程设计常常所在的区间),柔性拉杆力约为刚性拉杆力的80%~90%;当拉、压杆刚度比大于30%以后,柔性拉杆力已非常接近刚性拉杆力。
对于压杆力而言,拉、压杆刚度比对其影响则小得多,柔性拉压杆模型压杆力一般为刚性拉压杆模型压杆力的90%以上。
3 结语
通过对柔性拉压杆模型计算方法的理论推导,并结合实体有限元模型的分析对比,得出以下研究结论。
(1)现行规范采用刚性拉压杆模型计算,得到的拉杆拉力值较实际情况偏大,在结构尺寸确定的情况下,拉、压杆刚度比越小,偏大的程度越大。
(2)现行规范采用刚性拉压杆模型计算得到的压杆压力值较实际情况略偏大,拉、压杆刚度比对其影响程度较小。
(3)采用柔性拉压杆模型计算得到的拉杆力精度更高,与实体有限元模型结果更为接近,当采用有限元模型得到的主应力方向进行修正时,则基本上完全吻合。
(4)工程设计中对短悬臂盖梁结构可采用柔性拉压杆模型进行抗裂验算,计算简单,思路明晰,能满足工程精度要求,采用规范规定的压杆方向计算结果更偏于安全。

