基于ABAQUS的钢顶管屈曲分析

李 江

（中铁十九局集团轨道交通工程有限公司，北京市 101300）

0 引言

顶管法施工作为一种非开挖掘进式管道铺设施工工艺，由于对周围环境影响较小、综合成本低、管道整体性能好等优点得到了广泛的应用。但是由于钢顶管的直径、顶进距离和管道埋深的增加，大大增加了施工的难度。相比于混凝土管，钢顶管属于薄壁壳体，承载能力不仅与材料强度有关，很大程度上取决于它的屈曲临界荷载。

最早研究薄壁壳体结构的屈曲失稳机理可追溯到19世纪，Eluer对细长压杆的稳定性做了详细的研究，开创性地形成轴压圆柱薄壳的经典理论解[1]，后续诸多学者对圆柱薄壳的稳定性分析都是在此基础上作进一步的研究。20世纪上半叶，Lorenz、Von Mises等将Eluer所创经典理论应用到圆柱薄壳上，计算圆柱薄壳在均布轴压和均布围压下的临界荷载。但是后续经过实验证明，圆柱薄壳的实际屈曲荷载远小于经典理论解，并认为由于圆柱壳自身存在的初始几何缺陷[2]是导致实际屈曲荷载小于经典理论解的原因。

实际中钢顶管受力情况很复杂，而且结构形式也不同于经典理论解中的圆柱薄壳。由此可见，不能将圆柱薄壳的经典理论简单地应用到钢顶管结构的稳定性计算和分析中。故本文基于前人对圆柱薄壳和钢顶管稳定性的研究，采用理论计算和数值模拟相互验证的方法对钢顶管的稳定性进行分析研究。

1 有限元稳定分析方法

1.1 钢顶管简化受力分析

顶管施工过程中是钢管和土相互作用的过程，钢管受力情况随时间和顶进距离不断变化。为了方便分析，将受力复杂的钢顶管简化为一个独立结构，而将由液压油缸提供的顶力以及土体对钢管的作用简化为轴向和径向荷载施加在钢管上。简化之后，钢管所受荷载为管道端部的轴压、管道外壁的围压和管道外壁与土体之间的摩阻力[3]。对于管道外壁的围压，通过现场实测发现[4]，在注浆良好以及泥浆套形成良好的情况下，管道外壁来自周围环境的压力在注浆压力的作用下趋于均匀。在未采用注浆减阻的情况下，采用摩擦系数来确定摩阻力值；而在采用注浆减阻的情况下，则在顶管的设计计算中一般将其设为一个定值，大小一般为3～30 kPa[5]。故根据以上分析，将管道的外壁围压视为均布围压，管壁摩阻力为均匀分布，管道端部的迎面阻力为均匀轴压。

1.2 稳定分析方法

圆柱壳体的屈曲属于分叉屈曲。分叉屈曲是结构在达到临界状态后变得不稳定，直接进行弹塑性计算，则计算结果可能会与实际有很大出入。因此，实际计算中应先对结构引入某种初始缺陷，结构才会按照预先设定好的性态发生屈曲[6]。

基于几何完美和材料参数线性，ABAQUS中的特征值屈曲预测的主要作用是获取结构可能发生的屈曲模态[7]。当结构发生屈曲失稳时，则采用ABABQUS中的改进弧长法[8]来计算结构失稳临界荷载。

所以，本文数值模拟计算步骤为：（1）对钢顶管进行弹性分析，得到钢管可能的屈曲模态。（2）将一阶模态特征值与经典理论解进行对比，并作为初始几何缺陷乘以比例因子代入钢管。（3）进行弹塑性分析。

1.3 有限元模型

有限元分析采用ABAQUS中的BUCKLE分析步和RIKS分析步，基本模型的几何尺寸如下：管道长度取200 m来模拟长距离钢顶管，壁厚选取8mm、16 mm、20 mm、34 mm、48 mm。管道材料采用理想弹塑性模型，弹性模量E=206 GPa,泊松比v=0.3，屈服应力σcr=235 MPa。

管道材料采用理想弹塑性模型，采用Q235钢参数为计算基本参数。钢顶管直径和长度都比较大，因此选用三维壳单元来模拟，边界条件统一设置为一端简支，一端固定，计算模型如图1所示。

图1 钢管数值计算模型

2 钢顶管稳定性分析

2.1 理论分析方法

根据经典屈曲理论，可得到在均布轴压和均布围压下圆柱薄壳的失稳临界压力表达式[1]：

均布轴压下，圆柱壳屈曲荷载计算公式为：

均布围压下，圆柱壳屈曲荷载计算公式为：

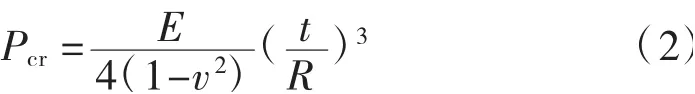
式中：E为圆柱壳弹性模量；v为圆柱壳泊松比；t为圆柱壳壁厚；R为圆柱壳半径；μ为有效长度系数，根据边界条件而变化，一端简支，一端固定为0.7。

2.2 有限元分析

由于有限元网格的类型和尺寸对最终计算结果和计算速率影响较大，故在用有限元进行数值模拟之前，需要预先对网格大小和类型进行一次优化。此次网格优化拟选用长度为150 m的钢管，壁厚为14 mm，网格类型为S4（四边形四节点壳单元）和S8R（四边形八节点缩减积分壳单元）两种作为对比，并选取不同的网格尺寸，计算结果如表1所示。

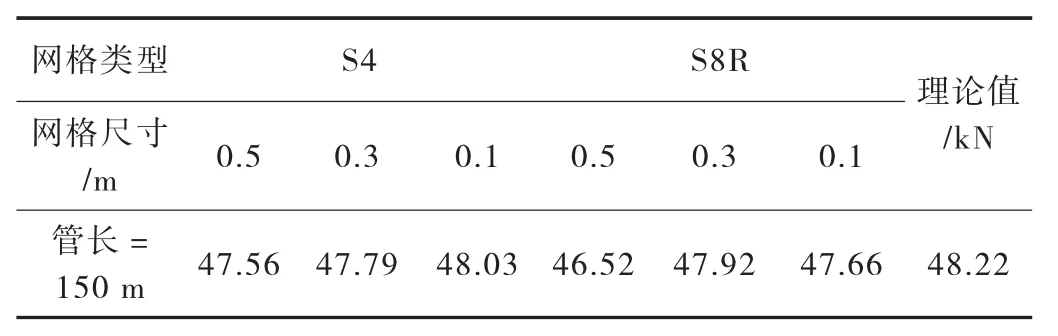
表1 网格类型与大小优化结果

由表1可知，网格类型为S4，网格尺寸采用0.1 m时，有限元计算结果与经典理论解较为吻合，故在后续计算中均选取此网格类型和尺寸。

故本文对钢顶管稳定分析的计算步骤为：（1）采用Buckle法进行均布围压和轴压作用下钢顶管的特征值计算，得到钢顶管可能发生的屈曲模态。（2）采用RIKS法进行弹塑性分析，所引入初始缺陷的大小不超过0.01D（D为管道外径）[5]，所得弹性和弹塑性计算结果如表2所示。

2.3 结果分析

长管在均布轴压和均布围压荷载作用下弹性和弹塑性计算结果如表2所示。弹性条件下将特征值计算的结果与经典的弹性屈曲理论值进行对比，可知长管在均布轴压和均布围压下的弹性屈曲荷载与数值模拟计算结果非常吻合。但弹性承载力并非管道的实际承载力，其未考虑材料非线性及几何非线性。管道实际的承载力需要将初始缺陷加入管道模型中，并考虑材料的塑性。在引入初始缺陷后,长距离管道在均布轴压作用下管道极限承载力与屈服理论值相差不小。说明长距离管道在轴压作用下，其极限承载力由其材料的屈服强度决定。长距离管道在均布围压作用下，缺陷的代入会使得管道极限承载力减小，逐渐趋于一稳定值。

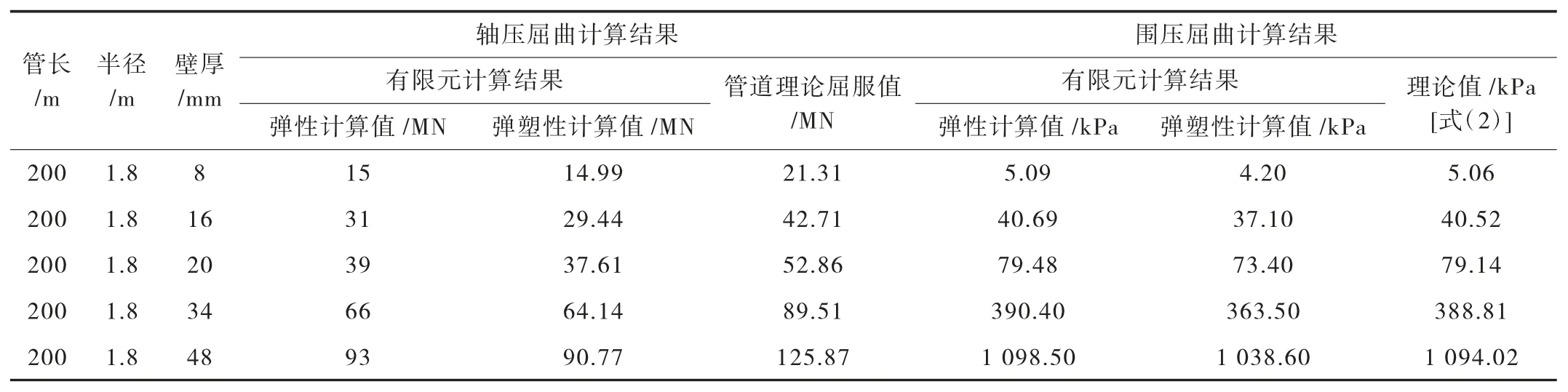
表2 数值模拟结果与理论值对比

由图2可知，在轴压荷载作用下，钢管整体屈曲模态与欧拉管较为接近。由图3可知，在围压作用下，长钢顶管呈现局部屈曲特征。

图2 轴压作用下钢管屈曲模态

图3 围压作用下钢管屈曲模态

3 结 论

顶管施工中钢管的受力状态十分复杂，目前还没有成熟的理论来研究钢顶管在施工中的稳定性。但采用数值模拟和理论相结合的方法，能在一定程度上高效直观地分析钢管的屈曲形式，计算钢管的屈曲临界荷载。

故本文采用ABAQUS对钢顶管进行有限元分析，得到了在不同条件下屈曲模态和弹塑性稳定极限荷载，并基于分析结果和经典理论解进行对比。由经典理论解和有限元计算结果来看，影响钢顶管稳定性的因素很多，其中壁厚是影响钢管稳定性的重要因素。由图4、图5可看出，壁厚的增加，会直接导致钢管的极限屈曲荷载在逐渐增加，但与此同时，壁厚的增加也意味着工程造价的增加。所以基于本文分析结果，在顶管设计与计算中应充分考虑经济性和钢顶管整体稳定性，来选取合适的壁厚。

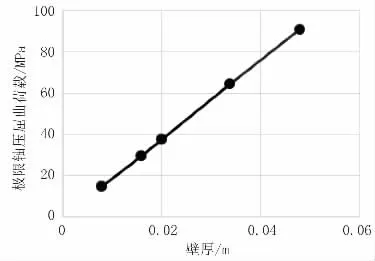
图4 壁厚与极限轴压屈曲荷载曲线

图5 壁厚与极限围压屈曲荷载曲线