考虑转动的双曲面球型减隔震支座竖向位移分析
史先飞,周彦锋,郑纪研,彭天波
(1.华设设计集团股份有限公司,江苏 南京 210000;2.同济大学,上海市 200092)
0 引言
经工程实践证明,桥梁抗震设计方法中减隔震设计是最经济、最有效的方法[1,2]。该方法依靠减隔震支座来完成减震和隔震目标,从而降低桥梁的震害。而双曲面球型减隔震支座因为具有构造简单、承载力大、耐久性好等优点,在众多减隔震支座中有着非常明显的减震效果[3-6],在连续梁桥中已得到了广泛的应用。
双曲面球型减隔震支座是利用大半径球面摩擦副代替球形支座的平面摩擦副形成的一种减隔震支座,其构造见图1。

图1 双曲面球型减隔震支座的构造示意图
该支座在使用过程中,会通过自身的水平位移和转动,以适应连续梁桥梁体自由伸缩和墩梁间转动的需要。而支座在发生水平位移和转动时,均伴随着支座竖向高度的变化。支座的竖向位移会对连续梁桥的内力尤其是曲线梁桥的内力产生很大影响[7],而对于高速列车桥梁,支座的竖向位移还会影响列车的行车安全[8]。因此有必要结合双曲面球型减隔震支座实际工作中的状态,对支座同时发生水平位移和转动时的竖向位移进行分析。
彭天波、李建中等[9]通过理论推导和试验验证,研究了水平位移下的双曲面球型减隔震支座的竖向位移,并分析了地震时该支座产生竖向位移的机理和影响因素,该文得到了只有水平位移的双曲面球型减隔震支座的竖向位移理论公式,见式(1)。
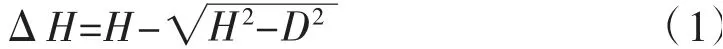
式中:ΔH为支座竖向位移;H为中支座板球心距,即两个曲面球心的距离;D为上下支座板间的水平位移。
然而只考虑水平位移下的支座竖向位移是不精确,因为该支座在工作时,不仅有水平位移,还有转动,但是目前由双曲面球型减隔震支座转动造成的竖向位移还没有相关的理论研究,也没有对该支座实际工作中同时发生水平位移和转动的支座竖向位移的相关研究。故本文旨在通过研究考虑转动的双曲面球型减隔震支座工作状态,用理论推导的方法得到支座的竖向位移,并分析其影响因素,为该支座设计和连续梁桥内力计算提供更精确和更合理的理论依据。
1 考虑转动的双曲面球型减隔震支座工作状态
为了研究考虑转动的双曲面球型减隔震支座竖向位移,首先应研究该支座考虑转动的实际工作状态。该支座的转动受墩梁转角约束,但其水平位移则可随着墩梁间水平位移的改变而改变,因此支座板间水平相对位移和支座转角是相互独立的变量。
双曲面球型减隔震支座初始状态和支座参数见图2,此时支座两个上下支座板之间没有转动,也没有相对水平位移。
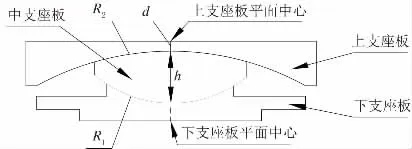
图2 双曲面球型减隔震支座初始状态
图2中:上支座板的中心厚度为d,中支座板中心厚度为h,中支座板的转动球面半径为R1,滑动球面半径为R2。定义中支座板两个球面球心距为H,则H=R1+R2-h。
参与工作的双曲面球型减隔震支座既有水平位移,又有转动。根据支座水平位移和转动之间的关系,可以把支座分为两种工作状态:(1)状态1为上支座板平面中心相对于下支座板平面中心朝着转角内部移动,见图3;(2)状态2为上支座板平面中心相对于下支座板平面中心朝着转角外部移动,见图4。

图3 双曲面球型减隔震支座工作状态1

图4 双曲面球型减隔震支座工作状态2
这两种支座的工作状态的区别是上下支座板间运动方向是相反的,两个支座板平面中心的竖向距离变化即考虑转动的双曲面球型减隔震支座的竖向位移。
2 考虑转动的双曲面球型减隔震支座竖向位移理论推导
如图3和图4所示,双曲面球型减隔震支座的竖向位移即上下两个支座板平面中心的竖向距离变化。可以取上支座板和中支座板为研究对象,计算支座工作时和初始状态时中支座板转动球面最低点与上支座板平面中心的竖向距离变化即可得到支座的竖向位移。以工作状态1为例,计算模型见图5。
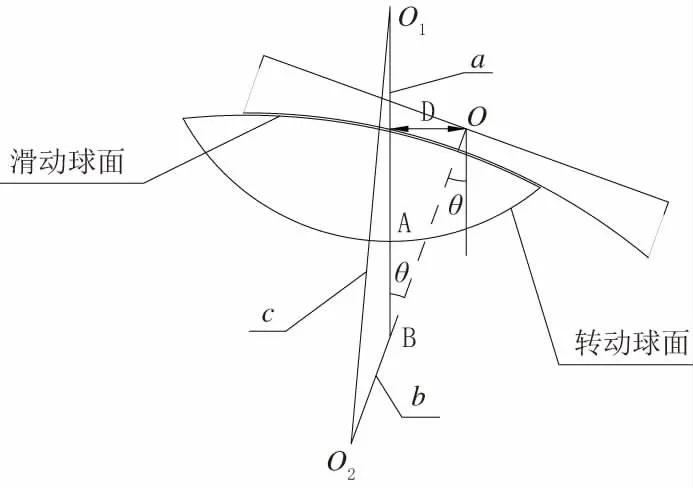
图5 竖向位移计算模型
图5中:O为上支座板平面中心,O1为中支座板转动球面球心,O2为中支座滑动球面球心,A点为中支座板转动球面最低点,θ为支座转动的角度,D为上下支座板间水平相对位移,工作状态1时D取正值,工作状态2时D取负值。
计算A点到O点的竖向距离,只需用B点到O点的竖向距离减去A、B两点的竖向距离即可。如图5所示,设O1与A之间的距离为a,O2与B之间的距离为b,O1与O2之间的距离为c,设初始状态时O与A之间的距离为H'OA,工作时O与A之间的距离为根据几何条件得:

取ΔO1BO2,利用余弦定理,可得:

解之得:
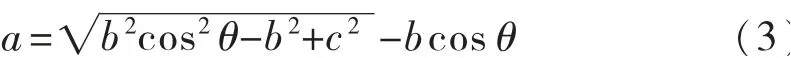
把b和c的值带入(3)式可得:
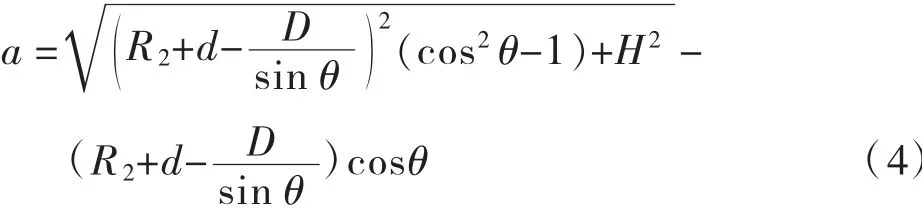
所以A点和B点之间的距离为:

因此可得A点到O点的竖向距离,为:
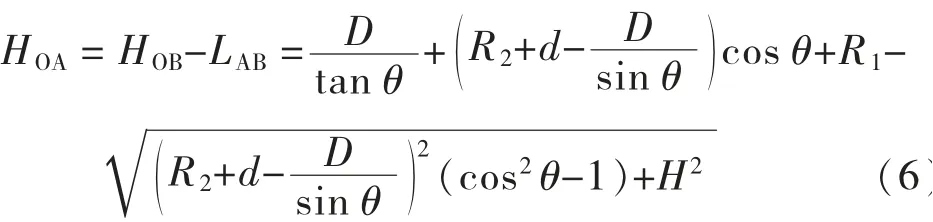
所以考虑转动的支座竖向位移为:


设m=(R2+d)(cosθ-1),n=(R2+d)sin θ,则式(6)转变为:

式(7)即为考虑转动的支座竖向位移公式,对比发现,式(1)为式(8)θ为0时的特例。
3 考虑转动的双曲面球型减隔震支座竖向位移的影响因素
根据式(8)可以发现,影响考虑转动的双曲面球型减隔震支座竖向位移的因素有H、D、R2+d和转角θ。为了更好的研究它们对ΔH的关系,本文取四种参数不同的支座,得到D和ΔH的关系曲线见图6,支座主要参数见表1。

图6 D与ΔH的关系
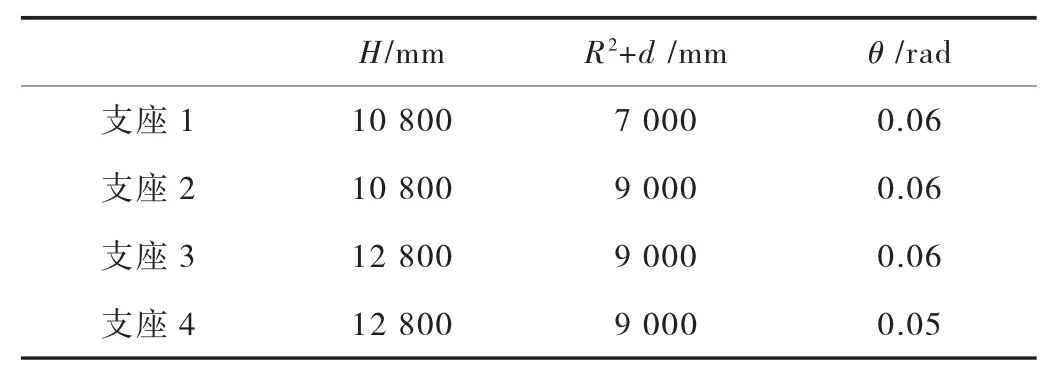
表1 三种不同支座的主要参数
由图6可知,D与ΔH近似抛物线的关系:当D取正值,即当考虑转动的支座在状态1工作时,随着支座水平位移的增大,支座竖向高度先减小,然后增大;当D取负值,即当考虑转动的支座在状态2工作时,随着支座水平位移的增大,支座的竖向高度一直在增大。
根据考虑转动的双曲面球型减隔震支座竖向位移式(8)可以发现,当D=n时,支座高度减小量最大,减小量为m值。由于m、n只与R2+d和转角θ有关,所以R2+d和转角θ对考虑转动的支座竖向位移影响最大,由图6四种支座的位移曲线也可以发现。球心距H对支座竖向位移的影响不是很大,主要对抛物线的开口大小有一定的影响,对比支座2和支座3可以发现,球心距越小的支座,D-ΔH抛物线开口越大,相同的D值对应的ΔH值越小。
4 结 语
本文建立了双曲面球型减隔震支座转动模型,能够很好的模拟该支座的两种情况的转动,即纯转和伴随水平位移的转动。接着通过理论推导得到了两种转动情况的支座转动竖向位移理论公式,并分析了影响支座转动竖向位移的因素,可以得到以下结论:
(1)双曲面球型减隔震支座的纯转会造成的支座竖向高度的减小,但减小量较小,随着R1和θ的增大而增大;
(2)随着支座板间水平相对位移的增大,伴随水平位移的支座转动会使得支座竖向高度先减小、后增大,R2和θ决定支座竖向高度减小时的支座板间水平相对位移的取值范围,R1、R2和θ决定支座竖向高度减小的最大值。
因此,在进行双曲面球型减隔震支座设计时,为了减小由于支座转动造成的竖向位移,应尽量选择中支座板转动球面半径较大、滑动球面半径较小、中心厚度较大的中支座板设计。对于墩梁间转角较大的连续梁桥,尤其在发生有支座板间水平相对位移的转动时,支座的竖向位移变化较大,在进行桥梁内力计算时,应把由于支座转动造成的竖向高度变化考虑进来,以提高计算的可靠性。

