利用知识互联破解初中“有理数除法”教学难点

陈洁

（上海市竹园中学 上海 200137）

一、简介

1.背景介绍

当前阶段，学生学习了沪教版教材预备年级下册第五章“有理数”前六节的内容。掌握了分数的乘除法相关知识，以及有理数的加、减、乘法的运算法则，即将开始学习第七节“有理数的除法”的内容。该节内容的教学重点是熟悉有理数除法的运算规律，掌握运算法则，确定商的符号，难点是灵活运用除法法则。根据以往的教学经验可知，初学时学生会遇到的障碍主要包括：①容易忽视除数必须非零；②不能便捷、清晰地确定运算结果的符号；③求解除数的倒数缺少方法。

2.本文贡献

本文通过分析学生在“有理数除法”学习中遇到的困难，总结教学经验和教学规律，设计了基于知识互联的“有理数除法”教学方法。该方法引导学生借助观察、思考、类比和归纳等方法，依据已经掌握的分数除法以及有理数加、减、乘法的运算法则，经历有理数除法运算规律的分析与推理，初步形成感性认识。基于知识互联的“有理数除法”教学方法，能够培养学生主动挖掘各知识点之间的相互联系，自主探索构建知识体系的能力。

二、基于知识互联的“有理数除法”课堂教学

本文将“有理数除法”的课堂教学划分为以下三个阶段：知识准备；知识互联探索；方法凝练。帮助学生依据已经掌握的知识点，自主探索整数运算、分数运算和有理数乘除法运算之间的知识互联，明确有理数除法的运算规律与性质，理解运算法则，培养学生构建知识体系的能力，促使学生从感性经验到理性认知的过渡，最终具备完成知识理论化描述的能力。

1.知识准备

知识准备是本教学方法的前导阶段，主要包括以下两个环节：（1）知识导入；（2）明确求除数倒数的方法。通过引导学生梳理分数除法运算中求除数倒数的方法，强调除数的取值范围，探索有理数除法的特点，及其和整数除法、分数除法的差异。本阶段的目的：借助乘除法运算的互逆关系，明确求倒数的方法和思考方式，将对有理数除法性质模糊认识逐步转变为清晰的运算法则做好前期准备工作，为建立有理数运算与整数运算、分数运算之间的联系奠定基础。

（1）知识导入

在课堂导入1中，学生可以通过观察整数除法中被除数、除数和商的符号之间的关系，类比整数运算法则，探索有理数除法运算法则，引导学生掌握从已知探索新知的数学学习方法，以及从直观思维到抽象思维的数学学习规律。

课堂导入1 口算：5×（-7）=__；（-5）×（-7）=__；35÷（-5）=__；35÷（-7）=___。

根据课堂导入1，请学生尝试归纳算法。

生1：两数相乘或者相除，如果是两个正数，结果就是正的。如果是一正一负，结果就是负的；

生2：两数相乘或者相除，同号为正，异号为负；

生3：两数相除，等于被除数乘以除数的倒数。

（2）明确求倒数的方法

利用课堂导入2和例题1，引导学生明确有理数除法运算和分数除法运算中求除数倒数方法的一致性。即先将带分数化为假分数，或者小数化为分数后，再将除数的分子与分母颠倒求其倒数，最后分析题目中标注各个字母取值范围的必要性。学生明确了求有理数倒数的方法与思考路径后，有必要将新知建构活动难度增大。笔者设计了例题2，求字母的倒数。设计的新问题再次引起学生的注意。在探索有理数运算与整数运算、分数运算乃至整式运算各知识点之间的联系过程中，培养学生数学思维的系统性和条理性。

课堂导入2 填空：①0÷4=____；② 0÷（-2）=____。

例题1：求下列各数的倒数：

例题2：求下列各数的倒数：

2.知识互联探索

知识互联是本教学方法的核心阶段。主要包括以下三个环节：（1）形成理性思考，总结有理数除法规律；（2）初步掌握规律；（3）练习巩固提高。有理数运算是对整数运算和分数运算的整合与拓展，因此它们的运算规律具有可比性。知识互联的教学方法即是依据有理数运算的上述特点，引导学生利用整数和分数的运算性质解决有理数乘除法运算转换的问题。本阶段的目的是：挖掘各个知识点之间的相互联系，将零散的知识编织成网，完善学生的知识体系，提升学生构建数学思维模式的能力。

（1）形成理性思考，总结有理数除法规律

在本环节中，利用例题3引导学生通过观察、思考、类比和归纳整数运算与有理数运算的知识内部联系，将感性认识以文字语言的形式表现，鼓励学生尝试自主突破教学重难点。学生从会做练习到熟悉有理数除法运算性质的过程中，厘清问题的本质，得到解决问题的通法，体会数学知识之间具有的关联性，强化对有理数除法运算法则的理解。

例题3：计算：

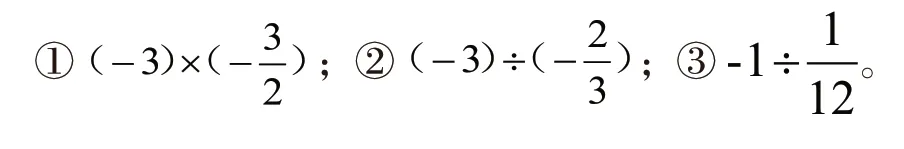
请学生再次尝试总结运算规律。

生4：除以一个数等于乘以一个数的倒数；

生5：除以一个分数等于乘以一个分数的倒数；

生6：除以一个不为零的数等于乘以一个不为零的数的倒数。

巩固练习：填空：有理数除法法则。

两数相除，____得正，____得负，并把____相除；零除以任何一个不为零的数，都得_______；除以一个_______，等于乘以________。

（2）初步掌握规律

本文的设计重点是熟悉有理数除法的运算规律，掌握运算法则。因此，教学过程中，借助例题4解决熟悉有理数乘除法运算逻辑顺序。常规的运算逻辑顺序是先确定结果的符号，然后将除法变为乘法，最后类比分数的运算完成化简，得到最终结果。在建立了分数运算、整数运算与有理数运算的知识互联后，学生初步具备化繁为简的能力，为提升解决数学问题的思维能力奠定了基础。

例题4：计算：

通过例题4，学生经历反复领悟有理数除法法则的过程。

生7：要将除法都变成乘法才能做；

生8：首先，观察题目中正负号的个数确定结果的符号，然后，通过求倒数的方法将除法转化为乘法后再做；

生9：如果乘除法中出现零，结果就为零；

生10：审题时先看有没有出现零，如果有，那么结果就为零。如果没有就先确定结果的正负号，然后除法都变为乘法，先化简，最后得到结果。

3.总结凝练

总结凝练是本教学方法的关键阶段，其包括从总结有理数除法运算的恒等变形规律，到凝练有理数除法的常规运算逻辑顺序，目的是培养学生在知识学习过程中从感性经验过渡到理性认知，从解决特殊案例拓展到解决普遍问题的能力。

（1）实现有理数除法法则表述

为达成教学目标，如果只是一味地增加练习会导致学生对于运算法则仅限于机械模仿和浅表理解，无法做到用已有的知识经验解决新情境中的问题。此处教学设计利用知识互联关注运算法则的细节辨析，加深学生对于有理数运算法则特征的理解，深刻地理解数学概念和法则等数学结论。

（2）建立思考模式

为了促使学生建立学习数学的思考模式，笔者设计了一道从具体的数字过渡到未知字母、从特殊到一般的变式练习，为今后学习整式除法和分式的除法建立必要的知识互联，做好前期的知识储备。

三、效果评估

为了验证本文所提出的利用知识互联破解初中“有理数除法”教学难点的方法应用有效性，分析该方法对于改进学生学习体验和提高学生掌握知识的程度的作用。笔者选取所教的六（1）班和六（2）班的学生参与实验。两个班级是平行班级，可以认为无显著差距。将1班作为实验班，采用利用知识互联破解初中“有理数除法”教学难点的教学方法；将2班作为对比班，采用传统的教学模式。

1.学生学习体验情况分析

教学结束后，针对两个班级学生的学习过程进行问卷调查。题目采用4级记分制：从“完全可以”“基本可以”“基本不能”到“完全不能”，依次计分4到1分。具体问卷见表1所列。

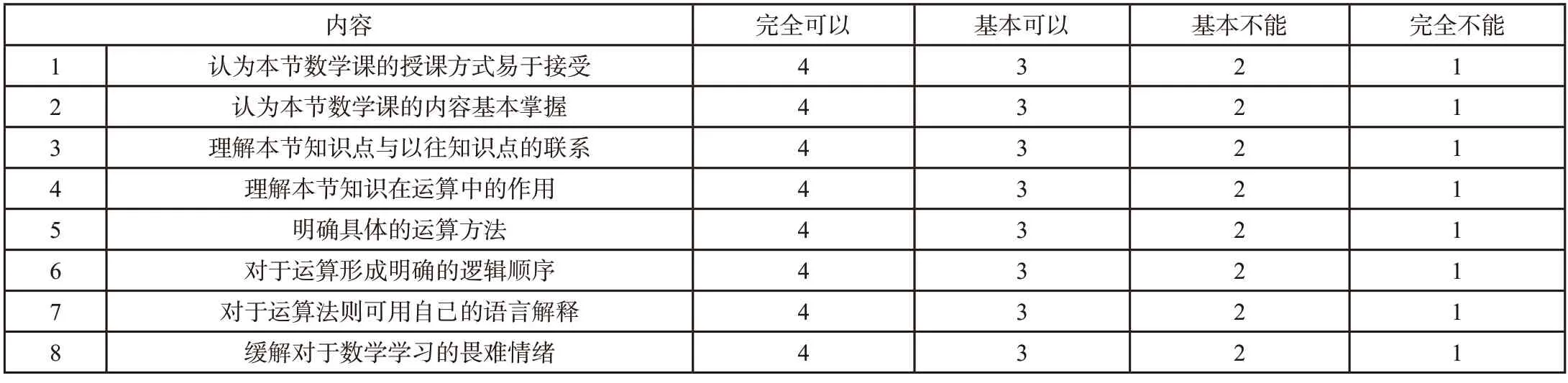
表1 学生学习体验问卷

利用知识互联的教学方法注重分析数学知识之间的互联，引导学生明确有理数除法运算的逻辑顺序和思维方法，帮助学生在学习过程中形成了清晰的解题思路，强化学生对于有理数除法法则的理性认识，从而缓解了学生对于本节课学习数学的畏难情绪[2]。问卷结果符合教学设计理念。实验班在第3个问题、第7个问题和第8个问题中得分明显高于对照班。说明利用知识互联破解初中“有理数除法”教学难点的教学方法，在培养学生厘清知识之间的联系和自主探索构建知识体系的能力方面具有显著的效果（图1）。

图1 学习体验分析表

2.学生知识掌握程度情况分析

笔者对两个班级进行数学测试检查学生课后的知识掌握情况。测试卷满分为100分，80分及以上为优良，60分及以上为及格，低于40分为低分。测试结果显示，实验班的均分高于对比班4.8分，优良率无明显变化，及格率高出接近14%，低分率低于对比班11.4%。说明利用知识互联破解初中“有理数除法”教学难点的教学方法对于学习成绩优良段的学生影响不大，但是能够明显提升班级及格率和降低低分率（表2）。

表2 数学测试成绩对比

结语

基于知识互联分析的教学方法，利用学生的已有知识结构基础和认知规律，在“有理数除法”的教学中进行实践应用。结果表明，该方法具有培养学生构建知识体系和明确数学学习逻辑顺序的能力，以及养成较好的思维模式等优点。在提升学生的学习能力方面表现突出，证明了其在教学实践中的有效性，能够较为容易地推广到一般其他的教学实践中，具有良好的普及价值。在完成知识的理论化描述和抽象表达的过程中，实现课程标准所提出“让学生学会自行获取数学知识的方法，体会数学思考和创造的过程”的目标。