基于均质化等效的点阵夹芯板仿真方法
邓梦,何敏,徐昉晖
(中国电子科技集团公司第十研究所,成都 610036)
引言
点阵材料是一种具有高孔隙率以及周期性结构的先进轻质多功能材料,可根据不同的受力环境实现每个微小单元的结构拓扑、单元数量与尺寸以及结构内局部的相对密度等参数的精确控制[1]。普遍情况下,点阵材料的相对密度仅是实体材料的十分之一,有利于设备的轻量化设计[2];同时,该类型材料还具有吸收环境噪音、减少冲击响应、屏蔽电磁辐射和提供减振阻尼等多功能特性,目前已广泛应用于航天航空飞行器、海军舰船、汽车等领域[3-5]。
研究人员通常基于实验方式对简单点阵材料的各项力学特性进行研究。Geng针对金属点阵材料与试验机夹持困难的问题提出了非接触式试验方法,成功测得了选择性激光熔炼制备的含菱形十二面体和BBC单元的AlSi10Mg点阵材料的弹性模量以及应力-应变关系曲线[6]。Xiao等通过单轴测试预测点阵材料的多轴屈服行为,提出了基于总应变能密度假设的点阵材料屈服准则[7]。Horn等利用四点弯试验研究了基于电子束选区熔化技术的等截面杆、不同尺寸和不同相对密度的菱形十二面体点阵材料的力学特性[8]。Khalil等提出了一种基于极端统计量和Crossland HCF准则的方法,研究了基本单元拓扑结构在比例多轴载荷下对几种类型单元结构抗疲劳性能的影响[9]。
然而,在点阵内部结构和外部尺寸先验优化设计阶段进行大量重复试验与测试会带来高昂的研制成本和漫长的设计周期,故完全基于实验方法研究复杂点阵材料的打印过程和材料性能可行性较差。在众多潜在的替代方法中,基于有限元方法的计算机辅助工程(CAE)技术可以显著缩短研究周期并降低工作成本,目前已广泛应用于点阵材料的疲劳分析[10]、优化设计[11-13]和生产制备[14]流程中。但目前的研究主要针对简单点阵材料本身的制造工艺和宏观特性,其结果对含有复杂点阵的零部件甚至整机设备的仿真分析与优化设计指导借鉴意义有限。
因此,本文采用了均质化等效的方法,将点阵材料均质化,对其材料特性进行等效处理,降低了含点阵材料的电子设备的仿真分析难度。
1 点阵材料均质化
点阵材料是由许多相同的点阵单元通过某种形式周期性的组合而成。点阵单元即胞元,点阵材料的均质化就是对胞元进行等效简化。
1.1 均质化等效方法
对胞元结构进行均质化等效,等效体的应力等于胞元结构的平均应力,等效体的平均应变等于胞元结构的平均应变,如式(1)和式(2)所示。


而等效体的平均应力和平均应变的本构关系模型如式(3)所示。

式中:
De—胞元结构的等效刚度矩阵。
因此,胞元结构的均质化等效主要是求解胞元结构的等效刚度矩阵。

式中:
D—有限元的通用刚度矩阵。
各向异性的材料的刚度矩阵有21个未知变量、正交各向异性的材料的刚度矩阵有9个未知变量,而各项同性材料的刚度矩阵只有3个未知变量。
对于各项异性的胞元结构,等效刚度矩阵有21个未知变量,而且胞元结构通常尺寸很小,通过材料试验的方式来获取等效刚度矩阵的难度大。因此,采用有限元仿真分析的方法来对胞元结构的刚度矩阵进行等效。
在求解胞元结构的等效刚度矩阵De时,以胞元结构的应变为仿真分析的边界条件,设计仿真边界使应变的第i个元素((ii))中的值不为0、其余元素的值为0,此时,De的第i列De(i)与当前边界状态下胞元结构的应力响应的关系为:

因此,胞元等效刚度矩阵的第i列的值可通过式(6)求解。

式中:
V—胞元结构的体积;
N—胞元结构网格单元的数量;
σn—第n个单元的平均应力;
△Vn—第n个单元的体积。
按上述方式依次进行六次求解,即可获得胞元结构的等效刚度矩阵De。
1.2 均质化等效结果
本文中研究的胞元结构如图1所示,选用的3D打印材料为AlSi10Mg,其材料特性如表1所示。

表1 AlSi10Mg材料属性

图1 胞元结构
按1.1节的方法对胞元结构进行等效处理,等效体的密度为924.35 kg/m3,等效刚度矩阵如表2所示。

表2 等效刚度矩阵(GPa)
2 仿真及试验方法
为研究1.2节求得的均质化等效结构能否准确模拟点阵材料在外界激励下的真实响应,分别对其进行了试验和仿真分析。
2.1 试验设计
夹芯板主体为点阵材料,并在其表面打印一层厚度约为0.5 mm的实心层,使其形成一个封闭的整体,如图2所示。
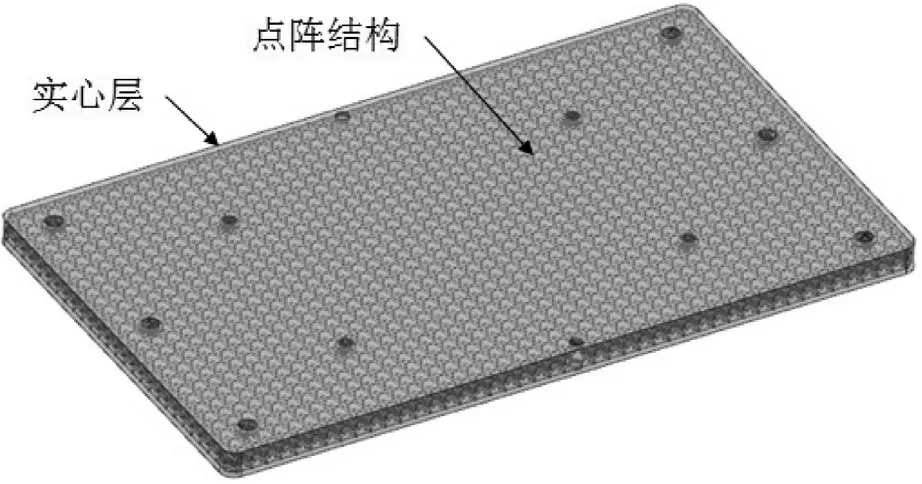
图2 夹芯板模型
振动试验激励条件为随机振动,激励频率范围为(15~2 000)Hz、幅值为0.01 g2/Hz;试验过程中采集夹芯板样件的中心、长短边中点三个典型位置的加速度响应信号,试验件装夹及传感器布局如图3所示。

图3 夹芯板装夹及传感器布局
2.2 仿真设计
在对试验板进行仿真分析前,需对试验板进行等效处理,将点阵特征区域进行填充形成均质化层,如图4所示。仿真分析时,均质化层采用AlSi10Mg均质化等效材料,实心层采用AlSi10Mg。两部分模型之间通过节点耦合方式的进行连接。

图4 夹芯板模型简化
为准确模拟设备在试验中的响应,仿真时将实验夹具也加入到仿真模型中,并采用梁单元模拟夹芯板和夹具的螺钉连接。通过夹具模型的安装孔施加固定约束,作为随机振动分析的激励源,如图5所示。仿真分析条件与振动试验条件一致,阻尼采用软件默认设置,即值为0.01的常数阻尼比。

图5 夹芯板仿真模型
3 结果分析
夹芯板随机振动试验的加速度测试结果如图6所示。由图6可知,测点3的响应结果与振动试验条件基本一致;测点1和测点2的响应结果在698.4 Hz和1 302 Hz处有明显的共振放大。

图6 夹芯板测试结果
夹芯板的模态分析结果如图7所示。在2 000 Hz的频率范围内夹芯板共有2阶模态,固有频率分别为701.7 Hz和1 406.4 Hz。与测试结果相比,仿真分析的前两阶固有频率的偏差分别为0.43 %和7.96 %。

图7 夹芯板模态分析结果
由图6可知,仅测点1和2处有明显的共振放大,因此,仅对比测点1和2的随机振动条件的仿真及测试结果,如图8和图9所示。
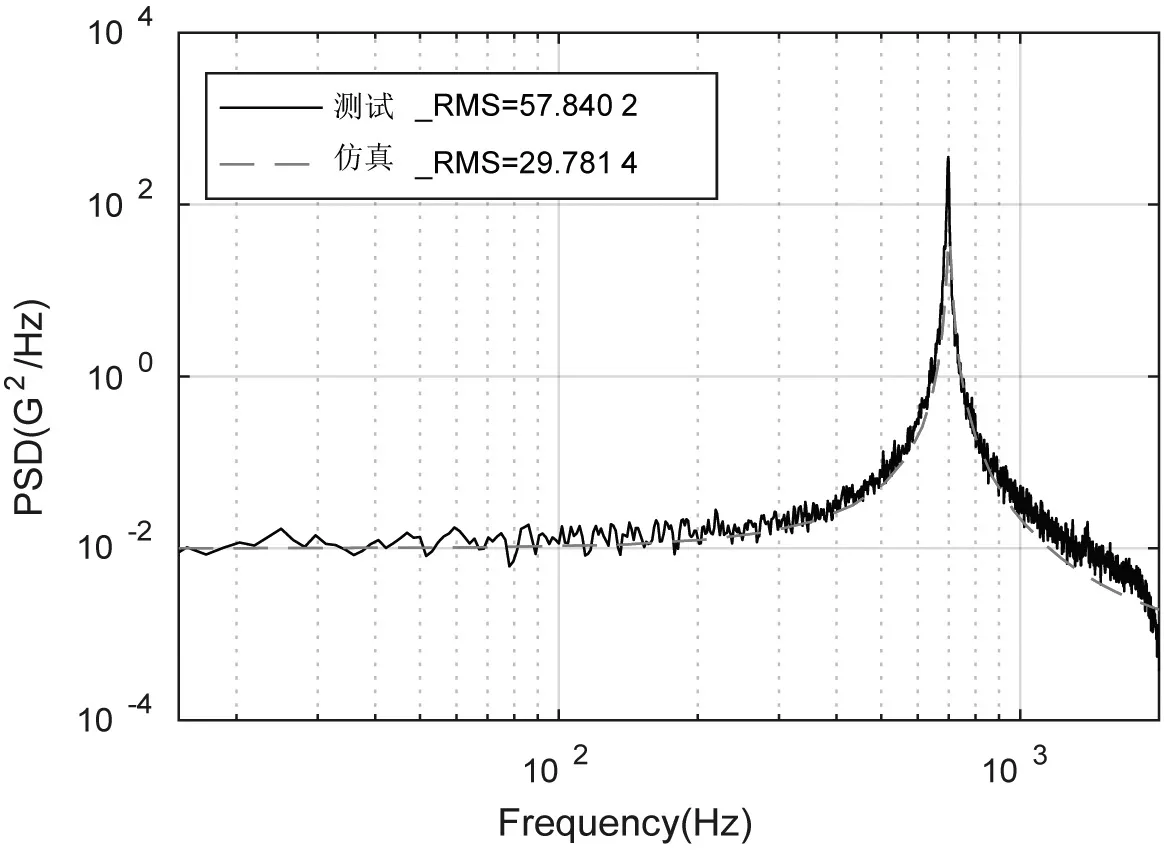
图8 测点1仿真测试结果对比
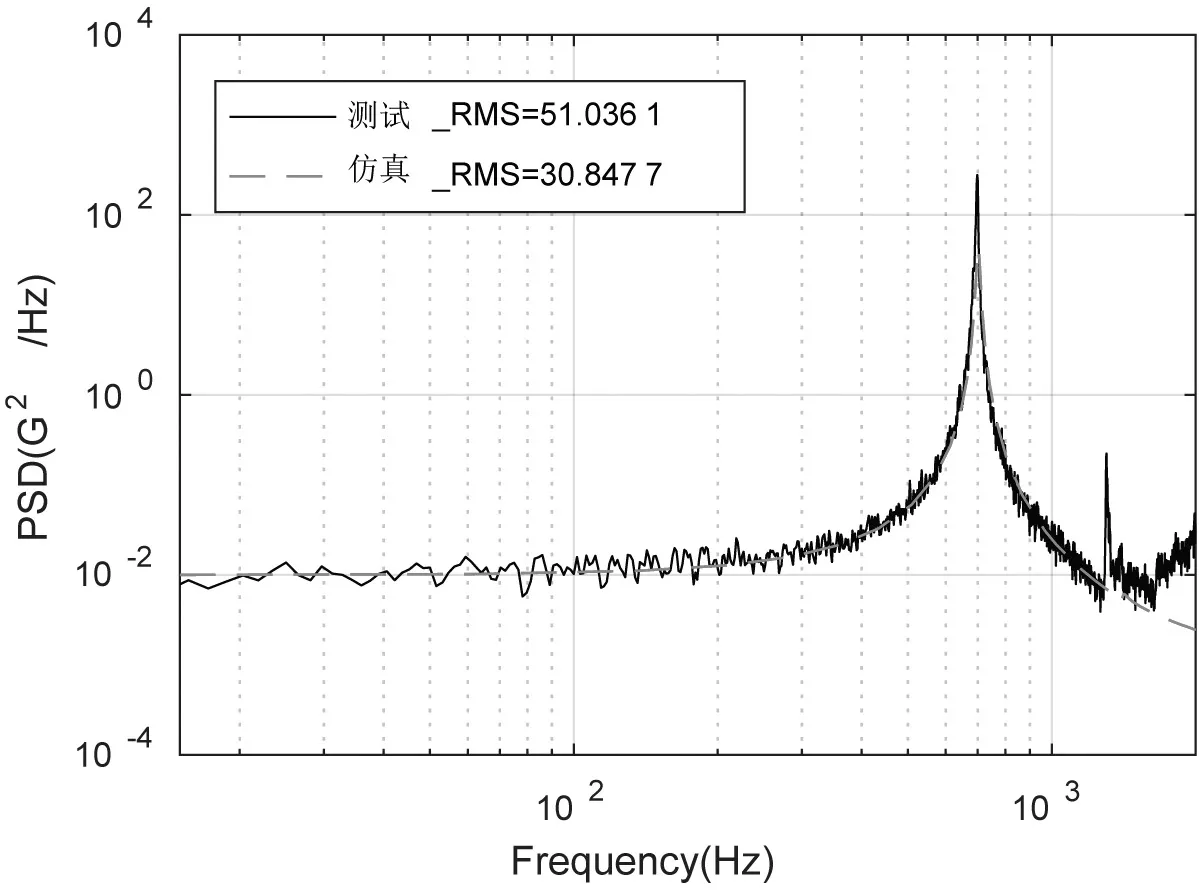
图9 测点2仿真测试结果对比
由图8和图9可知,两个测点的加速度响应的测试和仿真结果曲线的重合度较高,但其RMS值差距较大。这主要是由于仿真分析中设置的常数阻尼比的值与其实际值相差较大。通过修正仿真中的阻尼比参数,可对仿真结果进行修正,如表3、图10和图11所示。当阻尼比D=0.003 3时,测点1、测点2加速度响应的仿真曲线和测试曲线基本重合,且RMS值的相对误差最大值分别仅为-9.34 %和6.43 %。
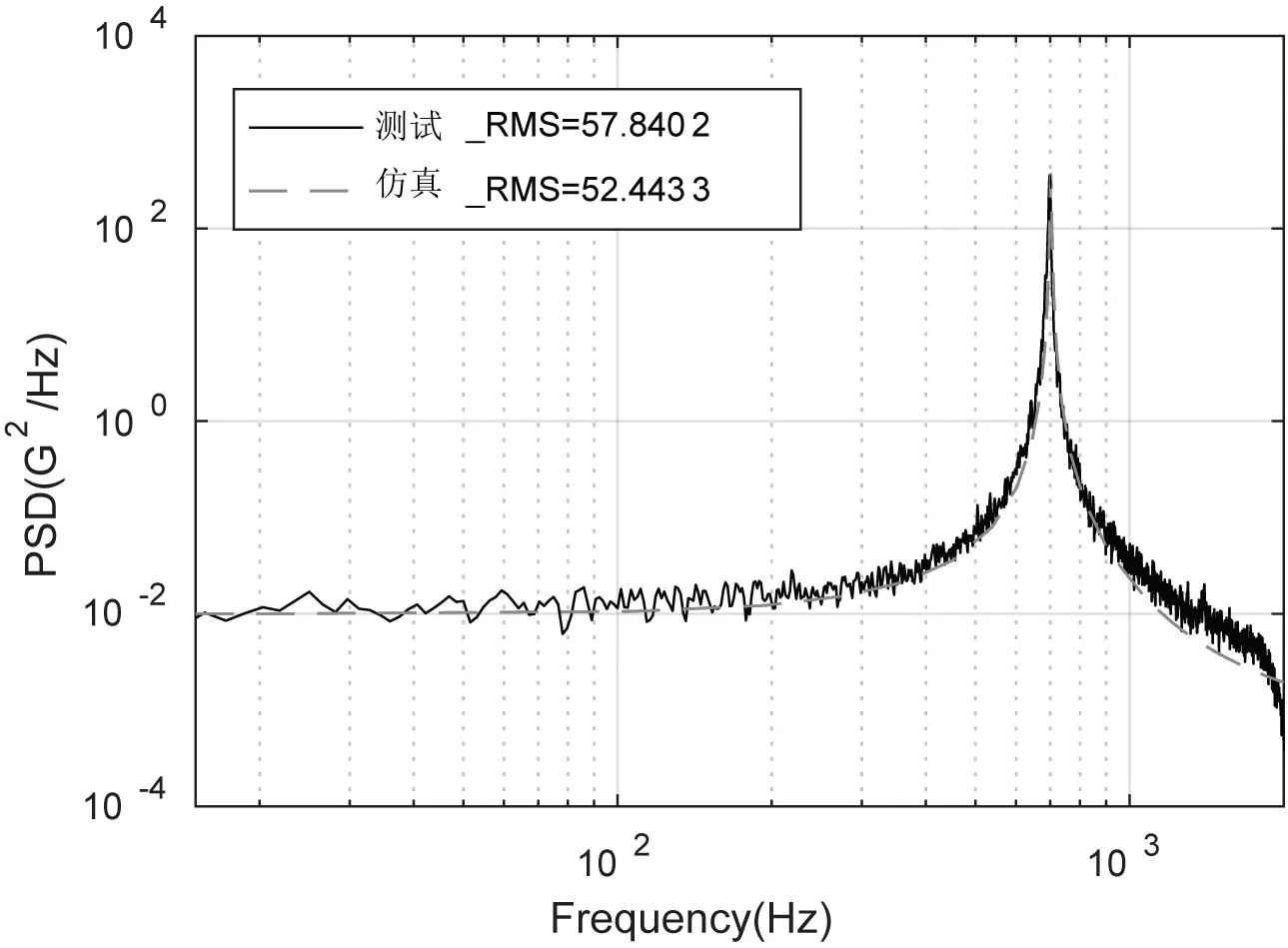
图10 测点1仿真测试结果对比(阻尼修正后)

图11 测点2仿真测试结果对比(阻尼修正后)

表3 仿真测试RMS值对比
4 结论
点阵材料是由许多相同的点阵单元通过某种形式周期性的组合而成,采用常规的有限元仿真分析方法,必然导致网格的节点数量过多而无法进行计算求解。本文提出了对点阵单元进行均质化等效的方法,使得含有大规模点阵单元的电子设备的有限元仿真分析成为可能。
对比仿真和试验测试结果可知,采用均质化等效后的有限元分析固有频率结果与试验相比最大误差为7.96 %,RMS值的最大误差为-9.34 %,证明本文提出的点阵材料均质化等效方法在大幅降低了仿真难度的同时能很好地模拟其力学性能。

