驾技术之舟 游千年之旅
——以圆锥曲线为例
刘梦哲 孔雯晴
(华东师范大学教师教育学院 200062)
1 引言
21世纪以来,随着计算机的日益普及,现代信息技术逐步进入课堂,突破了传统板书不能动态地展示数学图形、不够生动形象等瓶颈.国务院颁布的国家教育事业发展“十三五规划”(2017年)中提及要全力推动信息技术与教育教学深度融合,鼓励教师利用信息技术提升教学水平、创新教学模式.《普通高中数学课程标准(2017年版)》和《义务教育数学课程标准(2022年版)》都指出通过信息技术改进教学方式,促进学生学习方式转变,提高教学的实效性[1-2].由此可见,教师应当充分认识到信息技术在数学课堂教学中的价值,合理利用信息技术并发挥其作用.
圆锥曲线是高中解析几何教学的重要内容,椭圆、双曲线和抛物线的定义源自三维的“截线”,现行教科书中的二维定义对学生了解三种曲线间的关系和深刻理解定义的内涵造成了一定的障碍,因此,部分教师尝试将数学史融入数学教学,以此弥补这一空缺.例如,使用旦德林双球模型建立起椭圆的原始定义和第一定义间的联系[3],但是旦德林双球模型对学生的三维空间想象能力提出了挑战,如果教师使用不当,反而会增加学生的认知负担.倘若能以技术为辅,这样的困境便迎刃而解.
GeoGebra(下称GGB)是一款具有强大代数运算及绘图功能的动态数学软件,它能够将抽象的数学知识以直观的方式呈现,创设“多元联系表征”的学习环境,帮助学生深入理解知识的内在逻辑[4].尤其是在知识动态性方面,教师能够借助它呈现知识发生和发展的过程,帮助学生增强空间观念和空间想象能力,落实直观想象核心素养的培养.但是熟练使用GGB需要耗费较多的精力,由于受到技术水平的限制,在实际的教学中教师常常心有余而力不足.因此,本文以圆锥曲线作为抓手,介绍GGB在HPM教学中的应用,以期为教师教学提供参考.
2 GeoGebra在圆锥曲线教学中的应用举例
2.1 梅内克缪斯三线的绘制
公元前4世纪,梅内克缪斯(Menaechmus,约前380—约前320)用垂直于母线的平面去截三种不同的圆锥,得到三种不同的圆锥曲线,被后人称之为“梅内克缪斯三线”[5-6].
(1)绘制三种圆锥:顶角分别为直角、锐角和钝角的圆锥(图1).

图1 梅内克缪斯三线的绘制步骤之一
·在“绘图区”中分别绘制两根数值滑动条,名称分别为h和r,代表圆锥的高和底面半径.
·依次输入圆锥的底面圆心O(0,0,0)、顶点P(0,0,h),并输入指令“圆锥(O,P,r)”,由此得到一个底面半径为r、高为h的圆锥.
(2)绘制垂直于圆锥母线的平面(图2).

图2 梅内克缪斯三线的绘制步骤之二
·在“3D绘图区”中选择“多边形”选项,依次连接圆锥的顶点和圆锥与x轴或y轴的交点,作圆锥轴截面,记为△PAB.
·在线段PA上任取一点C,过点C作垂直于母线PA的平面.最后点击“相交曲线”选项,即可得到垂直于母线的平面与圆锥的交线.
(3)调整与优化.教师可以根据实际需求,隐藏相关坐标点或平面,并标注圆锥顶角的大小等.
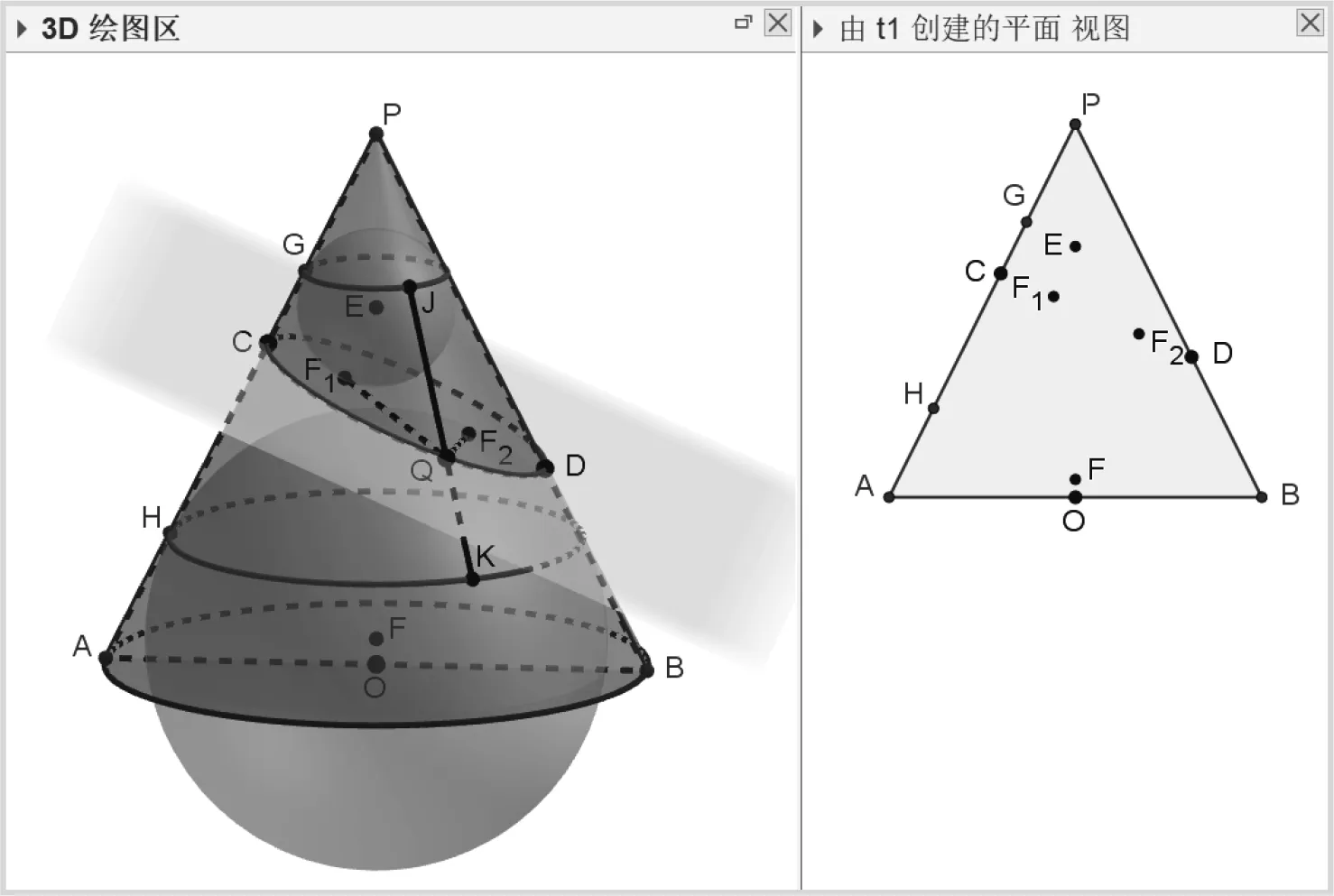
拖动两根滑动条,当r 2.2 阿波罗尼奥斯对圆锥截线的研究 古希腊数学家阿波罗尼奥斯(Apollonius,约前262—前190年)编著了《圆锥曲线论》,对前人的研究进行综合和创新.阿波罗尼奥斯是第一个使用同一正圆锥或斜圆锥来得到三种不同圆锥曲线的人,同时也是第一个发现双曲线有两支的人[6]. (1)绘制对顶圆锥. ·在已有两根数值滑动条h和r的基础上,再添加一根数值滑动条h1和两根角度滑动条α,β1; ·输入对顶圆锥的底面圆心“O(0,0,0)”“Q(0,0,2h)”及顶点“P(0,0,h)”,并输入指令“圆锥(O,P,r)”和“圆锥(Q,P,r)”,由此得到一对顶圆锥. (2)绘制与圆锥底面成β的平面. ·输入“u=(1;α,;β_1)”,并输入指令“垂直平面((0,0,h_1),u)”,于是得到与圆锥底面成β=90°-β1的平面.最后点击“相交曲线”选项,可以得到该平面与对顶圆锥的交线. (3)调整与优化.教师可以根据实际需求,隐藏相关坐标点或平面,并添加圆锥顶角及平面与圆锥底面的夹角等文本,便于学生归纳圆锥曲线的截线定义(图3). 图3 阿波罗尼奥斯截圆锥 通过动手操作,改变截面与圆锥底面所成二面角的大小,学生不难发现:当β=0,截线为圆;0<β<π,截线为椭圆;β=α,截线为抛物线;β>α,截线为双曲线. 2.3 旦德林双球模型 翻开历史的画卷,虽然数学家们先后给出了椭圆的圆锥截线定义和轨迹定义,并推导出了椭圆方程,研究了椭圆的性质,但这两个定义很长时间都彼此缺乏统一.直到1822年,比利时数学家旦德林(Dandelin)在一篇论文中利用圆锥的两个内切球,直接在圆锥上作出椭圆截面的焦点,导出椭圆的焦半径性质,从而证明了截线定义与轨迹定义的统一性,填平了古希腊圆锥曲线定义(截线定义)和17世纪新定义(今称椭圆第一定义)之间的鸿沟. 以椭圆的旦德林双球模型为例,利用GGB绘制需要经历圆锥及平面、双球、辅助线及调整优化四步. (1)圆锥及椭圆所在平面的绘制(图4). 图4 旦德林双球模型步骤之一 ·按照前面的方法,绘制出底面半径为r、高为h的圆锥,并利用“多边形”选项,作出圆锥的轴截面△PAB. ·在线段PA上任取一点C,PB上任取一点D,过点C作△PAB的垂线.最后,过这条垂线和点D作平面,再利用“相交曲线”选项,即可得到椭圆. (2)双球的绘制(图5). 图5 旦德林双球模型步骤之二 ·创建△PAB的平面视图,利用“直线”选项,连结PO,利用“线段”选项,连结CD.分别作∠PCD和∠CDB的角平分线,交直线PO于点E、点F,这两点即为所求双球的球心. ·分别过点E,F作线段CD的垂线,垂足为点G,H.将这两点重命名为F1和F2,易知,这两点是椭圆的焦点,于是线段EF1和FF2为双球的半径. ·回到“3D绘图区”,利用“球面”选项,分别作以点E为球心、EF1为半径的球和以点F为球心、FF2为半径的球. (3)添加相关辅助线(图6). 图6 旦德林双球模型步骤之三 ·在△PAB的平面视图中,过点E,F分别作PA的垂线,垂足为点G,H. ·在“3D绘图区”中,过点G,H分别作与z轴垂直的平面,由此得到双球与圆锥的交线. ·在椭圆上任取一点Q,利用“直线”选项,连结PQ,直线PQ分别交双球与圆锥的两条交线于点J,K.利用“线段”选项,连结QF1,QJ,QF2,QK. (4)调整优化(图7). 图7 旦德林双球模型步骤之四 ·创建椭圆的平面视图,由此可以让平面与圆锥的截线一目了然.当然,教师还可以隐藏不需要的点、直线或平面,改变点、直线或平面的颜色,同时在平面视图区创建文本,显示QF1+QF2及QJ+QK的长度等. 如图7,圆锥内含两球且与圆锥内表面相切,现用一不平行于母线且不经过圆锥顶点的平面去截圆锥,并与两球分别相切于F1,F2两点,可以证明其交线为椭圆[7].母线与两个球面相切于J,K两点.由球外一点Q向球引切线,其切线长相等,即QJ=QF1及QK=QF2,则QF1+QF2=QJ+QK=JK>F1F为定值.因此我们可以知道,椭圆上的任意一点到两个定点(即椭圆的焦点)之和为一个常值. 若在对顶圆锥中,我们也可以按照类似的方式作出圆锥的截线,并证明此截线为双曲线[7].旦德林双球模型的建立,不仅将古希腊的几何传统与截线定义有效结合,还帮助教师在今天的数学课堂中更好地采用发生教学法. 综上,信息技术宛如一缕和煦的春风,为数学教育注入了新的活力;信息技术宛如一艘巨轮,在数学的海洋里乘风破浪;信息技术宛如教育百花园中 一枝靓丽的奇葩,让数学教学变得多姿多彩.以网络和多媒体技术为核心的信息技术的发展,给教育带来了极大的挑战,也带来了新的契机.数学史的可贵之处并不只在于历史本身,而更在于发现探索的过程,是精神意志力和方法的体现.因此,数学教师有必要主动转变教育理念,将GGB与数学史深度融合,使数学教学实效得到提升,有效培养学生的数学素养. 其一,历历在目,培养学生的直观想象素养. 几何一直以来都是数学学习的重点和难点内容,从小学阶段起,学生先要接触一些最简单的几何图形,进而在初中阶段学习相关的初等几何知识,而到了高中,学生还需要学习解析几何和立体几何知识,可以说,几何知识一直伴随着学生.然而,一些学生普遍认为几何很抽象、很难学.因此,教师应努力寻找原因、摸索对策,以帮助学生摆脱“望几何生畏”的困境. 我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休.”GGB作为一款功能强大的数学软件,可以直观地揭示出“数与形”之间的内在联系,有助于实现数学知识的可视化、可理解化和可操作化.例如,在圆锥曲线的教学中,教师可以借助GGB,绘制平面截圆锥的立体图形,学生通过改变圆锥顶角的大小或圆锥截面的位置,发现圆锥曲线的截线定义,这一过程既有助于解答“为何椭圆、双曲线及抛物线统称为圆锥曲线”之困惑,又将加深对圆锥曲线的截线定义的理解与记忆. 由此可见,数字化软件的应用为数学教学打开了一扇新门.教师在几何教学中,应尝试利用GGB绘制几何图形,将原本抽象的图形变静为动,形象化地表达数学知识,从而打破“意会”与“言传”之间的壁垒.我们有理由相信,GGB必将成为培育学生直观想象素养的有效利器[8]. 其二,继往开来,强化学生的逻辑推理能力. 数学推理是数学思维活动的重要部分,数学运算、证明、作图等都蕴含着逻辑推理的成分,而GGB不仅可以助力几何图形可视化,还可以促进学生数学思维的发展. 一方面,借助GGB活跃思维,通过搭建几何图形,学生可以从可视化图形的制作过程中,思考每一步操作成立的依据.以制作旦德林双球模型中的一步为例,教师可以设置思考题:为什么∠PCD和∠CDB的角平分线与直线PO的交点是圆锥的两个内切球的球心(图5).显然,由对称性可知,双球的球心一定在面PAB中,由此问题可以转化为求△PCD的内切圆的圆心和求与AC,CD,DB三边相切的圆的圆心.在△PCD中,因为直线CE和PO分别是∠PCD和∠APB的角平分线,则两直线的交点即为△PCD的内心,同理可作出另一个圆的圆心. 另一方面,借助GGB发散思维,通过绘制动态图形,为数学概念的生成、数学定理的推导、数学公式的证明、数学问题的解答创造了无限的可能性.在探究圆锥曲线的截线定义的过程中,教师可以让学生借助手机或平板电脑上的GGB软件,亲自动手改变圆锥截面的位置,从直观上感受三条圆锥曲线的形成过程,并对此进行归纳,由此加深学生对圆锥曲线的截线定义的理解. 我们有理由相信,信息技术为数学史进课堂插上了腾飞的翅膀.GGB本身的直观性、有趣性的特点,可以帮助教师更好地使历史再现于数学课堂,使学生有身临其境的感觉,以数学史为载体促进学生对数学知识的本质理解,对于发展学生的思维、营造良好课堂的氛围,乃至促进教师专业发展都起到重要的作用.



3 结论与启示

