破思维定势 变思维角度 提思维品质
——例谈解析几何中与“联立”相关的思维定势
金一鸣 常梨君
(江苏省常州市田家炳高级中学 213001)
1 问题提出
思维定势(thinking set),也称“惯性思维”,是由先前的活动而造成的一种对活动的特殊的 心理准备状态,或活动的倾向性.在数学问题 解决中,思维定势对问题解决有积极的一面:利用已有知识、经验与当前问题情境建立联系,进行比较,把新问题化归成一个已解决的熟知旧问题. 思维定势亦有消极的一面:易产生思想上的惰性, 养成呆板的解题习惯.尤其当新旧问题形似质 异时,思维的定势会使解题者步入误区,造成知识和经验的负迁移,成为束缚创造性思维的一道枷锁.
面对解析几何问题,学生畏想、畏算,加之部分教师以考试得分为目的的引导,解答往往只有“三板斧”:一写标准方程,二列二元二次方程组,三用韦达定理.不可否认这种所谓“直线联立法”是解决直线与圆锥曲线相交的“通法”,但低级的思维定势必定阻碍了学生关键能力的培养与核心素养的提升,与新课程理念背道而驰.
2 常见思维定势及思维突破
新高考“反套路,反刷题”,关注数学本质,强调理性思维的价值,注重数学的基础性,突出关键能力的考查,引导学生对数学概念、方法有更深刻的认知.解析几何问题具有综合性强、运算量大、题目灵活多变等特点,是考查学生数学运算、数学建模和逻辑推理等核心素养的重要载体.笔者列举解析几何中与“联立”相关的常见思维定势,探讨如何破除思维定势,变化思维角度,提高思维品质,提升核心素养.
2.1 定势一:一定利用“直联法”
例1(2013年全国II卷文)设抛物线C:y2=4x的焦点为F,直线l过点F且与抛物线C交于A,B两点,若AF=3BF,则l的方程为( ).
A.y=x-1或y=-x+1

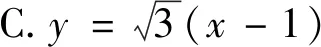

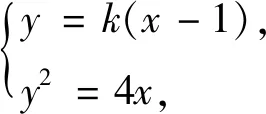
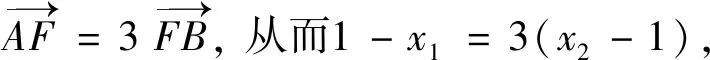
点评利用直联法(直线与抛物线联立+韦达定理)设而不求构造关于k的方程,是解决本题的常规思路.事实上,利用算两次思想,将AF=3BF进行双重解读,直接构造点坐标的二元方程,可以得到A,B是定点,进而求出斜率,此法更直接明了.
2.2 定势二:一定选择直线联立


(2)点A,B,D是双曲线C上不同的三点,且B,D两点关于y轴对称,△ABD的外接圆经过原点O,求证:直线AB与圆x2+y2=1相切.

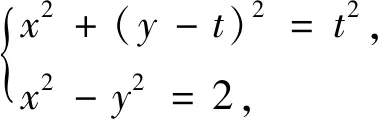
点评本题的关键之处在于如何利用y1y2=1得到双参数m,n之间的关系.以A,B两点为研究对象,利用其为三种曲线(直线、圆、双曲线)公共点的身份,将思维从直线与曲线联立中解脱出来,引入曲线与曲线联立,“算两次”得到m,n的关系式,从而简便求解.
2.3 定势三:一定利用直线消元
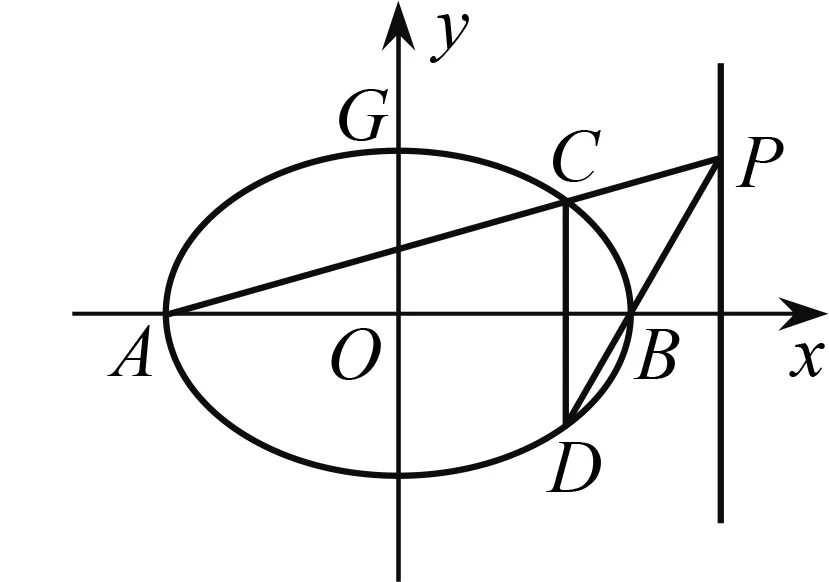
图1


(2)证明:直线CD过定点.
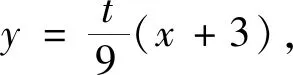

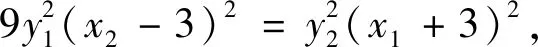
点评本题的关键是四元表达式3y1(x2-3)=y2(x1-3)的化简,利用直线x=my+n消元化为2my1y2+3(n-3)y1-(n+3)y2=0,但这个表达式“不对称”,直接利用韦达定理不方便,需要进一步转化.转换视角,利用点在椭圆上消元,可直接得到4x1x2-15(x1+x2)+36=0,后续求解自然水到渠成.
2.4 “联立”的教材溯源
翻阅人教A版选择性必修一,与联立相关的内容在解析几何各个章节中都有渗透,以具体的例题为依托,大多以“位置关系判定”“求弦长”为主.曲线方程“联立”的几何解释为:如果曲线C1:f(x,y)=0与曲线C2:f(x,y)=0有公共点,那么公共点满足曲线C1,C2的方程,即公共点坐标为方程组的解,方程组解的个数是公共点个数.据此判定直线与曲线的位置关系,解决相关后续问题.由上可知,联立只是一种手段,为何要联立?谁和谁联立?联立后消哪个变量?这些联立背后的底层逻辑需要厘清.
3 三点启示
3.1 形成定势,夯实解几之基
将几何对象坐标化、方程化,再进行代数讨论,最后把运算结果“翻译”成相应的几何结论,这就是用坐标法解决平面几何问题的“三部曲”.几何量的坐标化最终都可以归结到“点的坐标化”,联立的目的就是求点的坐标,如果点的坐标可解,那么整个问题就迎刃而解,但坐标求解后常为含参多元,所以常利用“设而不求”的思想.“直线与二次曲线联立”是解析几何在“代数讨论”中常用的一种通法,其解题模式如图2,这种解题模式能帮助我们快速解决一部分直线与圆锥曲线相交的问题.

图2
从行为主义的角度来看,学习是刺激和反应建立联系的过程,刺激呈现方式、反应后的强化以及重复练习的数量等是影响刺激与反应之间建立联系的主要因素.因此,对于解析几何教学,将“直线联立法”进行一定量的训练与强化并形成定势,可以有效缩短学生解决问题的时间,提升解题技能,提振数学学习的信心.
3.2 突破定势,回归解几之源
从“注重图形分析,巧妙坐标转化”着手,破除唯“直线联立法”论,探索解析几何解题的基本思路才是解析几何教学的方向.从不同视角将几何量坐标化,最终的化简结果殊途同归,但运算量却差异很大.以例1中“直线l过点F且与抛物线C交于A,B两点,若AF=3BF”这个条件坐标化为例(表1),已知F(1,0),设A(x1,y1),B(x2,y2).

表1
由上可以看出,解析几何的“坐标化”可以从位置关系(点、直线、曲线三者位置关系),距离(点点距、点线距、线线距),角(三角形内角、倾斜角、向量夹角)等方向入手.一方面,在定势突破过程中,教师要不断引导学生厘清解题思路与方法,明确相关解题方法的内在原理与底层逻辑;另一方面,教师要锻炼学生根据现有问题选择恰当解题方法的能力,让学生从解数学题走向解决数学问题.
3.3 体悟思想,提升核心素养
“形成定势”,再“突破定势”,使学生在“先立后破,破后再立”的过程中掌握解决解析几何问题的基本思路.学生解题的目的不能仅仅停留在获得答案的浅水区,而应该在数学问题的解决过程中,通过独立思考、自主学习、合作交流等多种学习方式,激发学习数学的兴趣,养成良好的学习习惯,促进实践能力和创新意识的发展.教师更要通过自身的引导,让学生领悟问题背后的数学思想,促进学生思维的提升,从而进一步促进学生数学核心素养的形成和发展.

