基于改进鲸鱼优化算法的近红外光谱波长变量选择方法及其应用

王仲雨，高美凤

（江南大学 轻工过程先进控制教育部重点实验室，物联网工程学院，江苏 无锡 214122）

与传统化学分析方法相比，近红外光谱分析技术具有快速、无损、简便、绿色环保等优点，广泛应用于石油化工、食品、药品、酿酒、烟草等众多领域，近年来已成为分析化学领域发展最为迅猛的技术之一。然而，在近红外光谱分析中，光谱数据往往包含成百上千个波长点，这些波长点含有的大量冗余信息和噪声将导致预测结果变差。因此，如何从众多的波长点中选择出能够提高预测模型稳健度和精确度的波长点变得尤为重要。当前，国内外学者提出了许多基于不同策略的波长选择算法。根据筛选光谱波长的方式，可将波长选择方法分为两类［1］：波长间隔选择方法和波长点选择方法。波长间隔选择方法包括：区间偏最小二乘（iPLS）［2］、向后区间偏最小二乘（biPLS）［3］、协同区间偏最小二乘（siPLS）［4］、移动窗口偏最小二乘（MWPLS）［5］和区间随机蛙跳（iRF）［6］等；波长点选择方法包括：基于PLS参数的变量在投影中的重要性（VIP）［7］，基于模型集群分析（MPA）的蒙特卡罗无信息变量消除（MC-UVE）［8］、变量组合总体分析（VCPA）［9］等，还有以智能优化算法为核心的组合波长点优化方法：如遗传算法（GA）［10］、粒子群算法（PSO）［11］、蚁群算法（ACO）［12］，以及新兴的智能优化算法——布谷鸟搜索算法（CS）［13］、萤火虫算法（DFA）［14］、灰狼算法（GWO）［15］等。尽管当前波长选择方法多种多样，但iPLS等波长间隔选择方法虽运算速度快但精度不高；GA等波长点组合优化算法预测精度很高但花费的时间成本太大。而鲸鱼优化算法［16］（Whale optimization algorithm，WOA）是一种新型的群体智能优化算法，通过模仿自然界座头鲸捕食行为来实现优化目的，具有原理简单、参数设置少等特点，本文拟在WOA的基础上提出一种时间成本小且预测精度高的波长选择方法。

波长选择实质上是在近红外光谱波长点中，选择最有效的波长点构建预测模型，并使预测精度最高。鉴于此，本文提出了一种新的波长变量选择方法——改进的鲸鱼优化算法（Improved whale optimization algorithm，iWOA）。首先，为了提升算法效率，本文效仿遗传算法将波长变量均分成若干波段，这些波段分别对应鲸鱼位置基因信息，位置基因采用二进制编码，“1”代表选择该波段，“0”代表不选择；然后对算法初始化种群进行改进，引入混沌策略初始化种群，以增加种群的多样性，避免算法过早陷入局部最优；其次是对二进制传递函数进行改进，提出了一种非线性的时变Sigmoid传递函数，使算法拥有良好的收敛性、较小的特征子集和更优的开发效率；最后将贪心算法思想引入到算法的迭代过程，即对当前迭代最优个体进行局部探优，进一步提升算法的探优能力，使模型获得更好的预测精度。

1 算法的原理及实现

1.1 鲸鱼算法的实现原理

二进制鲸鱼优化算法［18］应用于近红外光谱波长选择的步骤为：

（1）初始化种群，对鲸鱼个体进行编码：设置N个鲸鱼个体，将需要筛选的近红外光谱数据均分为L个波段，同样鲸鱼个体也有L维位置基因对应光谱数据的L个波段，位置基因“0”代表不选择该波段，“1”代表选择；对鲸鱼个体位置基因进行随机二进制0∕1编码。

（2）计算个体的适应度值，选出最优个体Xbest：将选择出的光谱波段进行PLS建模，适应度是关于RMSEC（校正集均方根误差）和Rc（校正集相关系数）的函数，适应度最高的个体为最优个体。适应度函数［16］为：

（3）开始迭代，更新鲸鱼的位置基因：鲸鱼位置更新方式有包围捕食、随机搜索和螺旋气泡3种。具体的更新方式如下：当随机数p＜ 0．5时，鲸鱼根据系数|A|的值选择更新方式，若|A| ＜ 1，采取包围捕食模式；若|A|＞ = 1，采取随机搜索模式。当随机数p≥ 0．5时，采取螺旋气泡模式更新鲸鱼位置信息，其中p在（0，1）之间。

1）包围捕食更新：

2）随机搜索更新：

3）螺旋气泡更新：

式中，和分别为第i只鲸鱼第t次迭代和t+1次迭代的位置，和分别为第t次迭代最佳位置的鲸鱼和随机位置的鲸鱼。b为对数螺旋形状的常数，通常取1，l为［-1，1］之间的随机常数，A和C为调节系数，如公式（5）表示：

式中，a= 2-2t∕tmax为线性收敛因子，其中tmax为最大迭代次数；r1和r2为［0，1］之间的随机数。

（4）经位置更新后的鲸鱼位置信息变成非二进制位置信息，在每次位置更新完成后再经式（6）和（7）进行二进制转换，式（7）中r3为［0，1］之间的随机常数。

（5）计算鲸鱼个体适应度值，更新最优个体。本次迭代结束，回到（3）继续下一次迭代，直至到达最大迭代次数tmax。

1.2 改进二进制鲸鱼算法

1.2.1 混沌策略初始化种群智能优化算法的寻优过程始于初始种群，而初始种群对算法的收敛速度和精度都有着深远的影响。传统的WOA算法由于不能借鉴任何先验知识，采用随机方式初始化种群，容易使得算法过早地陷入局部最优。本文引入混沌策略初始化种群，增加了种群的多样性，避免算法陷入局部最优，混沌策略具体的数学模型为：

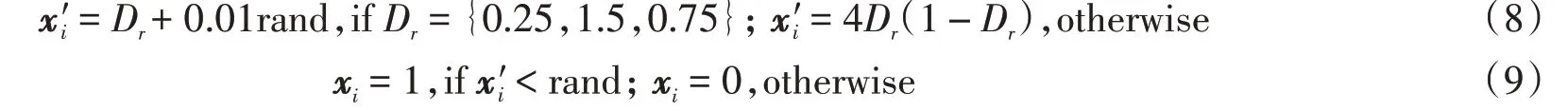
式中，x'i为混沌变量，xi为鲸鱼初始位置变量，Dr、rand为［0，1］之间的随机数。

1.2.2 非线性时变Sigmoid传递函数在二进制算法中，传递函数可能对算法的勘探、开发和收敛行为产生重大影响［19］。Sigmoid函数被广泛应用于二进制智能优化算法，但其不能平衡以上3种行为，因此本文提出了一种非线性时变的Sigmoid传递函数，可以使算法拥有良好的收敛性、较小的特征子集和更优的开发效率。

式中，α为常数，可以控制选取波长的数量和算法迭代的速度。当α = 1时，鲸鱼位置基因中“1”的数量很多，对应选择的波长数量也很多；当α = 6时，“1”的数量变少，对应选择的波长数量减少。由于α越大，算法选取的波长数量越少，故在考虑波长选择数目的同时，还要兼顾算法波长筛选后建模的精度，因此要选择合适的α使波长选择后建立的模型精度最高同时选择较少的波长数目。Tv为时变变量，具体为：

式中，t和tmax分别为当前的迭代次数和最大迭代次数，Tmax、Tmin为常数，分别取10和0．01。

1.2.3 引入贪心算法思想为了进一步提高模型的预测精度，将贪心算法引入到鲸鱼算法迭代过程中。贪心算法是指在对问题求解时，总是做出在当前看来最好的选择，即不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解，用局部最优构造全局最优，一步步靠近最优解［20］。具体的实施方案是：在每一次鲸鱼位置更新结束选出最优个体后，对最优个体进行局部寻优，即对最优个体位置信息随机取反，如果取反后适应度值大于最优个体，则保留；如果小于，再进行一次随机取反，直至得到大于最优个体的适应度值。如果重取次数达到上限值，则将原先最优个体直接替换最差个体。

1.3 iWOA具体实现步骤

Step1：通过混沌策略初始化种群，对个体进行位置基因编码。设置N个鲸鱼个体，将光谱数据均分为L段，对应的鲸鱼个体含有L个位置基因，使用混沌策略对鲸鱼种群初始化。

Step2：计算当前个体的适应度值，选出最优个体xbest。

Step3：开始迭代，初始化A、C、a、p、b、l和迭代次数t等参数值，按照公式（2） ～ （5）进行鲸鱼位置基因的计算。

Step4：引入非线性时变Sigmoid传递函数对鲸鱼位置基因进行二进制转换。

Step5：计算当前迭代鲸鱼个体适应度值，更新最优个体。

Step6：引入贪心算法思想。对每一次迭代中适应度最优的个体基因进行局部性探优，即随机取反一个位置基因。若取反后的个体适应度大于取反前，则保留；否则再一次随机取反一个位置基因，若到达最大取反次数，则将最优个体取代最差个体。

Step7：本次迭代结束，返回（3）继续下一次迭代，直至到达最大迭代次数tmax。

2 实验部分

2.1 实验数据

2.1.1 实验数据来源为了验证改进的波长选择算法对于建模的有效性，将改进的iWOA算法应用在一组玉米数据上。该数据集引用自eigenvector网站上开源的玉米样本光谱数据集，为700个玉米样品分别由m5spec、mp5spec、mp6spec仪器扫描得到的光谱数据，包含水、脂肪、蛋白质、淀粉的含量值，光谱的波长范围为1 100 ～2 498 nm，采样间隔为 2 nm，共 700个波长点（图1） 。本文拟采用m5spec仪器采集的玉米数据集。

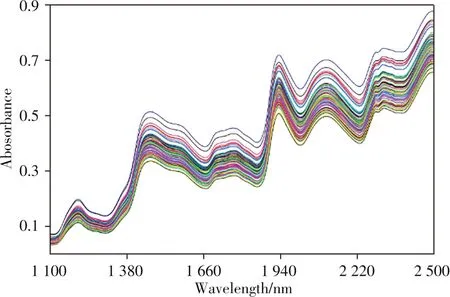
图1 原始光谱图Fig．1 Original spectra

2.1.2 样本集划分本文采用Kennard-Stone（K-S）方法将80个样本分为52个校正集和28个预测集。校正集和预测集的各部分含量值统计见表1。由表1可知，校正集样本与预测集样本的平均值（Avg）和标准差（Std）相差不大，说明通过K-S方法划分的数据集，保证了校正集样本均匀分布。

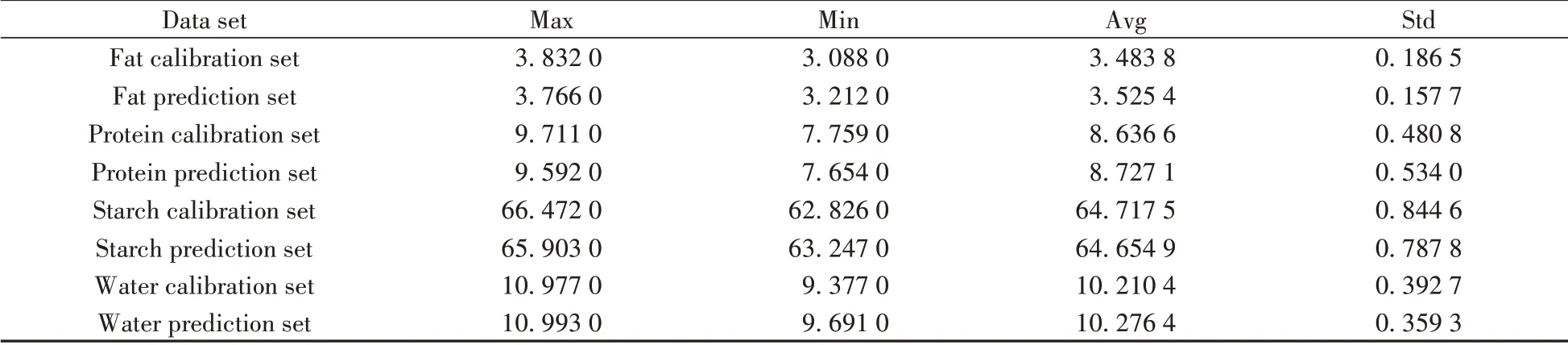
表1 校正集和预测集中的脂肪、蛋白质、淀粉和水的含量值统计Table 1 Statics of fat，protein，starch and water content in correction and prediction sets （g∕100 g）

2.2 实验设备

本研究使用的是一台三星笔记本电脑，处理器是Intel（R） Core（TM） i5-7300HQ，CPU主频2．50 GHz，Win10、64位操作系统，显卡为GTX1050。本实验所有运算均在MTLAB 2018a上进行。

2.3 实验方法

为了验证改进的iWOA算法对模型预测的有效性，将其与使用原始光谱、GA算法、WOA算法建模的预测结果进行对比。

群体智能算法不仅可以选择波长点，也可以选择波长段，而选择波长段可以大幅度减少波长选择的运算量，提升算法运行效率，且合适的波长段数还可提升预测精度，因此本文采用波长段选择方法。将1 100 ～ 2 498 nm范围的700个光谱数据均分为L段，分别取L为35、70和140进行实验，结果显示当L取70时，算法的效率和预测精度最高，即对应鲸鱼个体包含70个位置基因，每个基因位代表10个波长点。对于iWOA算法，设置50个鲸鱼个体，使波长选择后建立的模型精度最高同时选择较少的波长数目，非线性时变Sigmoid传递函数的参数α设置为6，贪心思想重置次数设置为5，最大迭代次数100；对于GA算法，设置50个染色体，交叉概率0．85，变异概率0．1，最大迭代次数200；对于WOA算法，设置50个鲸鱼个体，最大迭代次数100。由于3种算法均具有随机性，最后结果为算法运行50次后求均值。

3 结果与讨论

3.1 算法改进效果分析

3.1.1 非线性时变Sigmoid传递函数和贪心算法思想的改进效果为验证传递函数改进和贪心思想改进的效果，对WOA算法和iWOA算法分别测试脂肪、蛋白质、淀粉、水50次的RMSEP值进行考察（图2）。由图2A可知，脂肪经WOA算法筛选后建立的预测模型的RMSEP值在0．070 0左右，改进传递函数后降至0．050 0左右，而改进传递函数并同时引入贪心算法思想后RMSEP降至0．033 0左右；蛋白质经WOA算法筛选后建立的预测模型的RMSEP值在0．110 0左右，改进传递函数后降至0．080 0左右，改进传递函数并同时引入贪心算法思想后RMSEP降至0．050 0左右；淀粉经WOA算法筛选后建立的预测模型的RMSEP值在0．240 0左右，改进传递函数后降至0．170 0左右，改进传递函数并同时引入贪心算法思想后RMSEP降至0．140 0左右；水经WOA算法筛选后建立的预测模型的RMSEP值在0．025 0左右，改进传递函数后降至0．006 0左右，而改进传递函数并同时引入贪心算法思想后RMSEP仍在0．006 0左右，变化值不大，这是由于此时的RMSEP值已经很小。因此，两种改进方案都能提高建模后的预测精度。

图2 WOA和iWOA算法运行50次的RMSEP值Fig．2 RMSEP values for WOA and iWOA algorithm runs 50 times

3.1.2 混沌策略初始化种群和3种改进方法结合的效果为验证混沌策略初始化种群和iWOA的改进效果，以玉米蛋白质数据集为例，比较了随机策略-WOA、混沌策略-WOA和iWOA 3种算法的收敛性，以3种算法模型预测性能指标的适应度函数值（F）为标准，结果如图3所示。随机策略-WOA算法的适应度函数值在迭代次数为80时达到饱和；混沌策略-WOA在迭代次数为40时即达到饱和，且适应度函数值相较随机策略-WOA算法有所提升，说明混沌策略初始化种群可以起到避免算法过早陷入局部最优的作用。iWOA算法在迭代次数为50左右时适应度函数值达到饱和，说明混沌策略、贪心算法思想和非线性时变Sigmoid传递函数3种改进方案结合的iWOA算法的收敛性能依然良好，且适应度函数值相较随机策略-WOA和混沌策略-WOA算法显著提升，模型的预测性能得到显著改善。

图3 不同方法的适应度值随迭代次数的变化图Fig．3 Fitness value for the different methods vary by iteration

3.2 波长选择频率分析

图4是iWOA算法分别在玉米脂肪、蛋白质、淀粉和水数据集上运行50次后，各个波段变量被选取的频率分布直方图。

由图4A可知，脂肪近红外光谱被iWOA算法选择的频率在15次以上的变量波段有：1 700 ～1 760 nm、2 260 ～ 2 320 nm，而这些区域与脂肪中C—H伸缩振动的一级倍频和二级倍频、C—H变形振动的一级倍频以及O—H伸缩振动的一级倍频的频率一致；由图4B可知，蛋白质被选择的频率在15次以上的变量波段集中在2 120 ～ 2 220 nm，这些区域与蛋白质中N—H伸缩振动的一级倍频、C = = O伸缩振动的一级倍频以及C—H伸缩振动的一级和二级倍频等的频率一致；由图4C可知，淀粉被选频率在15次以上的变量波段有：1 680 ～ 1 700 nm、1 740 ～ 1 780 nm和1 980 ～ 2 000 nm，这些区域与淀粉中C—H伸缩振动的二级倍频、O—H伸缩振动的一级倍频频率一致；由图4D可知，水被选频率在15次以上的变量波段有1 900 ～ 1 920 nm和2 000 ～ 2 020 nm，这些区域与水中O—H伸缩振动和变形振动的二级倍频频率一致。

图4 iWOA运行50次后波长变量被选择的频率Fig．4 The frequencies of the wavelength variables selected after running 50 times iWOA

对筛选的高频波段对应官能团进行分析，所选的波长点均能很好地反映该指标的特征信息。因此，本算法可以起到剔除光谱数据中冗余信息和噪声、消减光谱变量间多重共线性问题的作用，使建立的预测模型更加稳定有效。

3.3 预测结果对比

为了验证算法的有效性，将iWOA与原始光谱以及GA、WOA波长选择算法进行比较，分别构建脂肪、蛋白质、淀粉和水4种成分的PLS预测模型，以算法的运行时间、选择出的波长变量数目、校正集相关系数（Rc）和均方根误差（RMSEC）、预测集相关系数（Rp）和均方根误差（RMSEP）作为评价标准，以上各指标都采用50次求均值，标准差（SD）为50次RMSEP值的标准差，结果如表2所示。上述评价指标中，同一成分PLS建模时选择的主因子数相同；算法选择的波长数越少，预测模型的复杂度越低；校正集相关系数和预测集相关系数越大，模型的稳定性越好；校正集均方根误差和预测集均方根误差越低，模型的预测精度越好；同样，算法花费的时间越少，建模的效率越高。

从表2可知，在玉米脂肪、蛋白质、淀粉和水含量的预测上，相比于原始光谱，iWOA模型的RMSEC分别从0．076 9、0．122 4、0．258 2、0．050 4降至0．024 1、0．039 3、0．104 9、0．004 4，Rc分别从0．909 1、0．966 4、0．951 2、0．991 6提升到0．990 5、0．9962、0．991 6、0．999 9；RMSEP分别从0．077 2、0．122 4、0．334 4、0．059 5降至0．033 2、0．050 7、0．139 2、0．004 4，Rp分别从0．866 8、0．972 4、0．902 4、0．985 7提升至0．972 3、0．994 8、0．981 9、0．999 9。说明经iWOA算法波长选择后建立的预测模型的稳定性和精度均得到了显著提升。而对于水含量的预测，由于原始光谱的预测精度已经很高，因此经波长选择后的各项指标并未能取得特别好的结果。与WOA和GA相比，iWOA算法波长选择后建立的模型具有最高的相关系数、最低的均方根误差，并且选择的波长数目最少，算法花费的时间最少，算法效率最高，但RMSEP的标准差（SD）相比其他算法略有增大，说明RMSEP值的波动性偏大，因此iWOA算法应用于生产活动中需要多次采样求均值。

表2 不同波长选择方法在玉米4个指标校正集和预测集上的性能Table 2 Performance of different wavelength selection methods on 4 index correction sets and prediction sets of maize

4 结 论

本文提出了一种新型的近红外光谱波长选择方法，即改进的鲸鱼优化算法（iWOA），对原算法提出了3种改进措施：混沌策略初始化种群、引入非线性时变Sigmoid传递函数和贪心算法思想。经iWOA算法波长选择后，基于玉米脂肪、蛋白质、淀粉和水的近红外光谱数据建立的预测模型性能优于其他波长选择算法：筛选出的变量数目最少，降至80个左右，降低了模型的复杂度；模型的预测精度最高，脂肪、蛋白质、淀粉和水的预测集均方根误差RMSEP分别降至0．033 2、0．050 7、0．139 2、0．004 4；筛选过程花费的时间最少，在3．5 s左右，算法的运行效率最高。本文提出的改进措施可为其他智能优化算法的应用与改进提供一定的参考，同时该算法在各方面的高性能使之有望广泛应用于近红外光谱的波长选择。