旋风分离器蜗壳半径对物料分离性能的影响

凌光磊，刘云峰，黄 涛，杨柳松，高延民，任林海

1洛阳矿山机械工程设计研究院有限责任公司 河南洛阳 471039

2智能矿山重型装备全国重点实验室 河南洛阳 471039

3洛阳栾川钼业集团股份有限公司 河南栾川 471500

旋风分离器是一种将气体和物料分离的装置，它利用高速旋转的气流，使得物料产生离心力，进而物料被分离器收集[1-2]。旋风分离器因其结构简单、性能稳定、适用各种恶劣环境，成为矿业生产当中的重要设备之一[3-4]。

旋风分离器在工业生产作业中，出现了物料返混、顶部积灰等问题，影响其工作效率。这些问题可以通过优化旋风分离器的结构进行解决，例如蜗壳半径、内锥筒参数等。目前国内外学者对旋风分离器结构优化做了许多努力。K.Elsayed[5]对不同截面入口的旋风分离器进行了数值模拟，得出结论：入口宽度越大，压差越小，但分离效率下降。周发戚等人[6]为了研究旋风分离器顶部上灰环现象，采用二次风入口结构，分离器顶部磨损大大降低，分离效率增加 2%，能耗减少 16.8%。金有海等人[7]对旋风分离器进行了结构参数增大，研究旋风分离器的直径对分离性能的影响。袁怡等人[8]采用 Stairmand 型旋风分离器进行试验分析，探究筒径对旋风分离器性能的影响，认为入口气速不变，筒体直径加大，会导致压差升高、分离效率降低。杨柳松等人[9]采用不同内锥长度的旋风分离器进行研究，发现内锥筒长度不影响旋风分离器的分离效率。范军领等人[10]进行了α型旋风分离器放大效应的数值分析。蜗壳半径不仅影响分离器的分离效率，对系统的能耗也有重要作用。目前，业内开展旋风分离器蜗壳半径对其性能的影响研究尚不充分。因此，开展旋风分离器蜗壳半径变化对其性能的影响研究具有重要意义。

1 研究模型及计算条件说明

1.1 旋风分离器三维模型

为了探究旋风分离器蜗壳半径对其分离性能的影响规律，本文以生料粉磨系统配用的 2-6800 型旋风筒为研究对象，开展相关的研究计算。旋风分离器总体结构相对简单，主要由入口、内锥筒、筒体段及锥体段等部分组成，如图 1 所示。

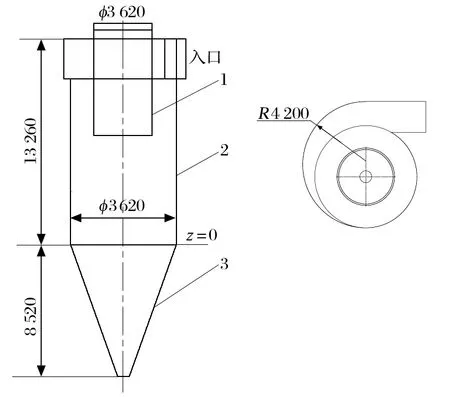
图1 旋风分离器几何结构及尺寸Fig.1 Geometry and dimension of cyclone separator

1.2 计算湍流模型选择

旋风分离器内部空气、物料颗粒之间的相互作用十分复杂，通过理论计算对其进行研究十分困难。通过数值模拟分析软件对旋风分离器的性能进行研究是一种行之有效的方法，也取得了一系列的研究成果。旋风分离器内流体高速旋转流动，研究计算时选用了在分离流方面有着不错表现的 RNG 模型，粒子入射采用随机轨道的 DPM 模型。此湍流模型考虑了平均流动中的旋流情况，并且其模型以各向同性涡粘性的Boussinesq 为假设基础，主要针对充分发展的湍流模型，该模型中的k和ε如式 (1)、(2) 所示：

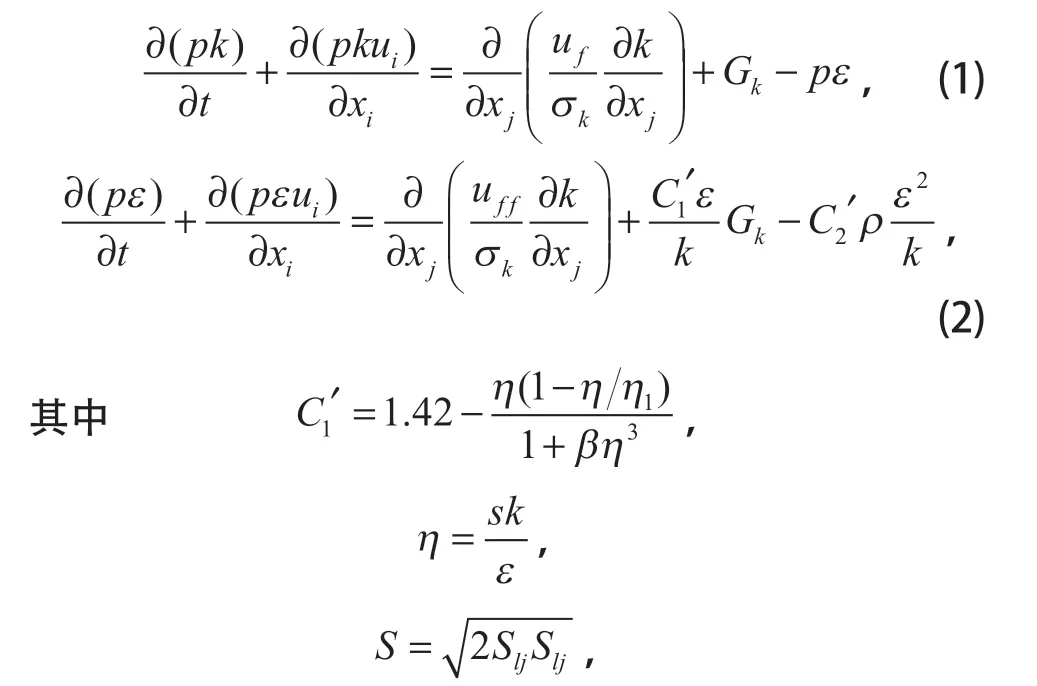
式中：η1=4.28；β=0.015；σk=σε=0.7179；C2'=1.68。

1.3 研究边界条件及参数设定

旋风分离器边界条件需要结合实际工况进行设定，以保证模拟结果的准确性。旋风分离器中流体设置为空气，密度为 1.225 kg/m3；处理风量 (工况) 为 360 000 m3/h；入射气流含尘质量浓度为 500 g/m3；物料颗粒的相关计算参数如表 1 所列。

表1 物料颗粒的计算参数Tab.1 Calculation parameters of material particle

计算边界的相关参数设置如下：入口气体的速度设为vin=19.53 m/s，其边界条件是速度入口，离散相边界采用 DPM 入射；出口设置为流出出口 (Outflow)，离散相采用逃跑边界 (Escape) 边界；壁面采用标准的反弹函数进行处理。

2 研究方案及结果分析

2.1 研究方案说明

以数值模型方法为手段，研究旋风分离器的蜗壳半径变化对其压力场、速度场、压差、分离效率的影响。本文制定了 4 种蜗壳半径结构方案如图 2 所示。分别是结构 A、结构B、结构 C、结构 D，具体结构参数如表 2 所列。结构 A 蜗壳半径数为 0，也可称之为直切式旋风分离器。

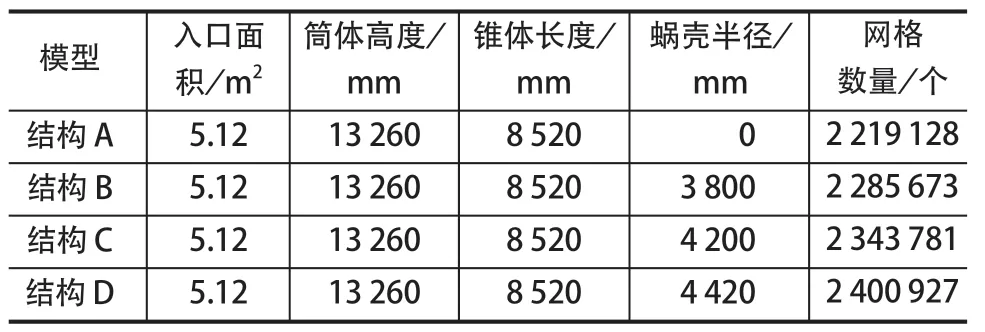
表2 4 种蜗壳结构的具体参数Tab.2 Specific parameters of four kinds of volute

图2 4 种蜗壳结构方案Fig.2 Structural scheme of four kinds of volute

2.2 网格划分及无关性验证

旋风分离器网格划分采用的尺寸不同，得到的网格数量差别很大，对最终的计算结果和计算量有非常大的影响。在开展相关研究计算之前，有必要对旋风分离器的网格数量和计算结果之间的关系作出验证性计算，保证以最合理的网格数量得到满足要求精度的计算结果。通过控制结构 C 旋风分离器网格数目，将入口与出口之间的压差作为参考值，进行计算验证，结果如图 3 所示。

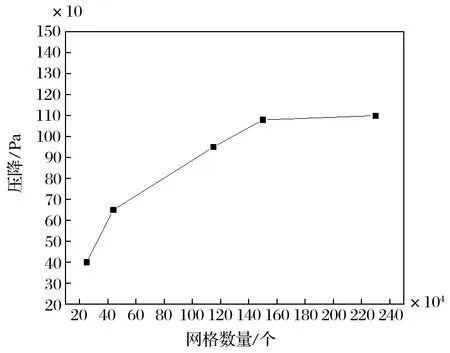
图3 不同网格数量下，进出口压差的变化 Fig.3 Variation of pressure difference between inlet and outlet at various quantity of grid

由图 3 可知，随着网格数的增加，出入口之间的压差变化幅值比较大；当网格数量增大到 230 万个以上时，出入口之间的压差趋于定值。

2.3 研究结果分析

对上述 4 种研究方案进行计算研究，将得到的计算结果在各个方面进行对比分析，分析过程及结果如下。

2.3.1 压力场分析

图4 所示为不同蜗壳半径的旋风分离器在中心轴截面 (x=0) 处的静压分布云图。由图 4 可知，静压呈轴对称分布，壁面处静压高，轴心处静压低；旋风分离器蜗壳半径越大，近壁面的静压越大；4 种结构的近壁面静压依次为pA=1.55 kPa，pB=1.63 kPa，pC=1.75 kPa，pD=2.35 kPa。壁面静压越大，颗粒在壁面处受到压力越大，颗粒更容易沿壁面向下运动，从而被锥体底部收集。在轴心附近存在负压区，负压由内锥筒一直延伸到锥体底部，负压的存在正是旋风分离器内锥筒物料颗粒短路的原因。

图4 不同蜗壳半径下，旋风分离器静压分布云图Fig.4 Static pressure contours of cyclone separator at various radius of volute

2.3.2 速度场分析

图5 所示为不同蜗壳半径的旋风分离器在z=1.2 m 截面速度分布云图。由图 5 可知，旋风分离器蜗壳半径越大，其在z=1.2 m 截面上最大速度越大，4 种结构的速度依次为vA=37.7 m/s，vB=38.8 m/s，vC=40.2 m/s，vD=43.88 m/s；随着蜗壳半径的增大，旋风分离器的最大风速区逆时针偏移，且内锥筒壁面处的速度增大。蜗壳结构处的速度增大，使得颗粒在此处获得的速度增大，有利于提高分离效率；内锥筒壁面处的速度增大，减少了颗粒的二次返尘。

图5 在 z=1.2 m 截面，不同蜗壳半径下，旋风分离器速度分布云图Fig.5 Velocity contours of cyclone separator at various radius of volute on section of z =1.2 m

2.3.3 切向速度分析

切向速度是研究旋风分离器分离性能的重要指标。图 6 所示为不同蜗壳半径的旋风分离器在中心轴截面 (x=0) 处的切向速度分布云图。可以看出，切向速度呈 Rankine 组合涡特征，最大切向速度在轴线附近，锥体底部速度为负值；随着蜗壳半径的增大，气流的切向速度增大。锥体底部的速度为负值，是由于此处静压为负值，它是粉尘返混的重要原因之一。为了更明确蜗壳半径变化对筒体空间内切向速度的影响，分别选取z=4 m、z=5 m、z=6 m、z=6.5 m 截面处的切向速度，进行对比分析。

图6 不同蜗壳半径下，旋风分离器切向速度分布云图Fig.6 Tangential velocity contours of cyclone separator at various radius of volute

图7 所示为不同蜗壳半径的旋风分离器在不同高度处切向速度。由图 7 可得，旋风分离器筒体空间内切向速度呈轴对称分布，壁面处切向速度为零，轴心处速度较小；随着蜗壳半径的增大，最大切向速度增大，这是由于在蜗壳结构内切向加速度不变，蜗壳半径增加，加速距离增大，导致切向速度增大；当蜗壳半径为 4 420 mm，切向速度有较大幅度的增长；筒体切向速度增大，使得环形空间内的颗粒的离心力增大，颗粒移动到壁面，颗粒从而沿着壁面向下运动，因此提高分离效率。轴心处切向速度较小，颗粒易被上行流携带向上运动，从内锥筒排出，从而造成短路。

图7 不同蜗壳半径下，旋风分离器在不同高度时的切向速度Fig.7 Tangential velocity at various height of cyclone separators and various radius of volute

2.3.4 轴向速度分析

旋风分离器的气流可以分为近壁面的下行流和中心区的上行流，下行流是颗粒被收集的主要原因。图 8 所示为不同蜗壳半径的旋风分离器在不同高度处的轴向速度。由图 8 可知，轴向速度呈 M 形分布，随着蜗壳半径的增大，最大轴向速度增大；随着截面高度的增大，轴向速度增大。z=6 m 截面邻近内锥筒进口，因而选择此截面进行分析。由图 8(b) 可知，随着蜗壳半径的增大，轴心处的轴向速度减小 (结构 D，在 4 420 mm 此处发生了特异情况)，减少短路的可能，提高了旋风分离器的分离效率。

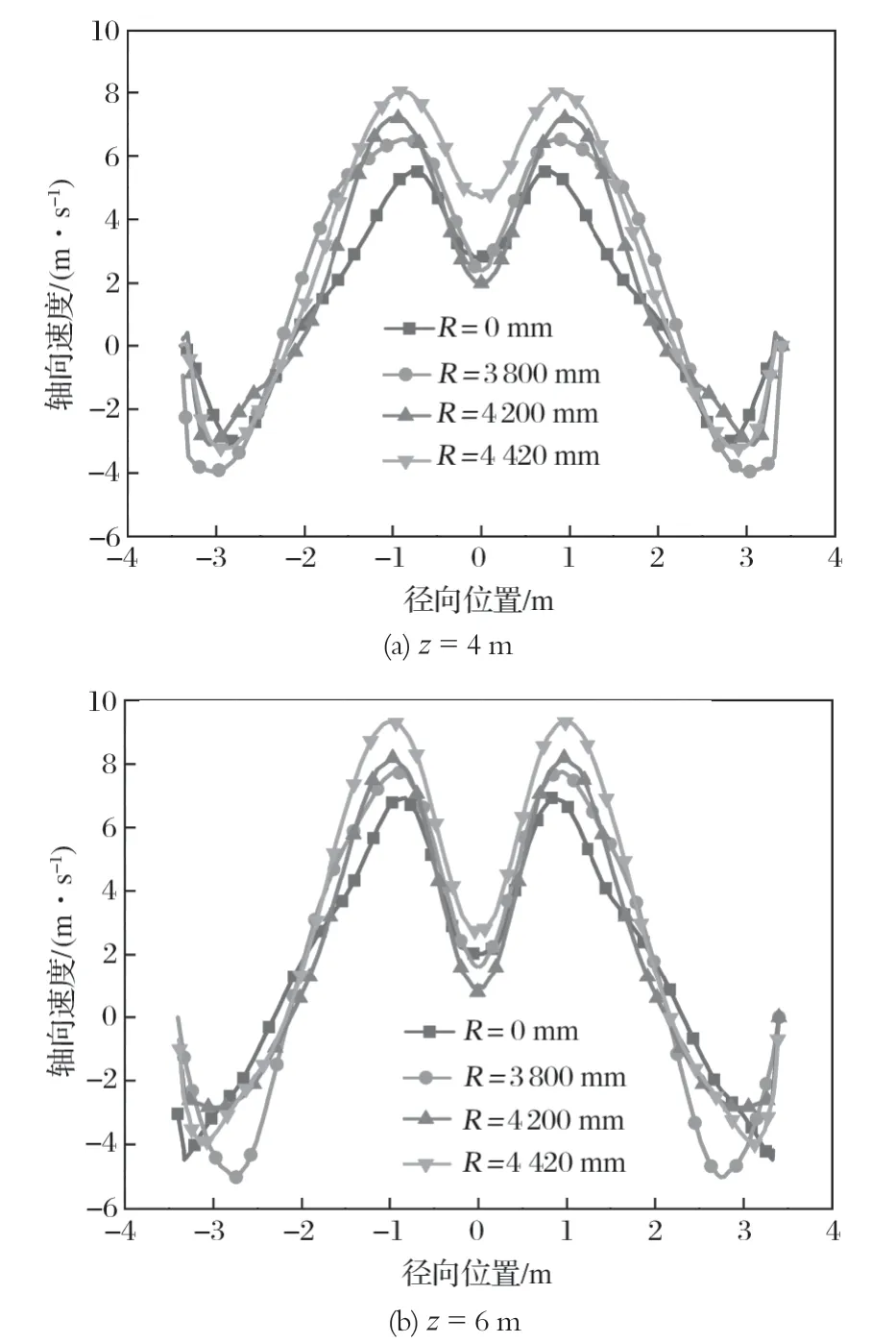
图8 不同蜗壳半径下，旋风分离器在不同高度时的轴向速度Fig.8 Axial velocity of cyclone separator at various height of cyclone separator and various radius of volute

2.3.5 分离效率与压差

旋风分离器中有三部分颗粒：进入颗粒 (mf)、捕集颗粒 (mc) 和排放颗粒 (me)，三者之间的关系为

分级效率是指收集的某一粒径范围内物料颗粒占总物料的比值，其公式为

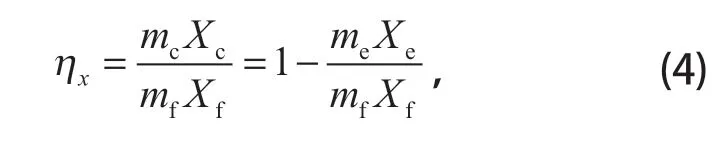
式中：Xf、Xc、Xe为进入、收集和逃逸颗粒某一粒径下的质量分数。

图9 所示为不同蜗壳半径的旋风分离器的颗粒分级效率。由图 9 可知，随着旋风分离器蜗壳半径的增大，分离效率增大，对于粒径大于 25 µm 颗粒，分离效率为 100%。旋风分离器分级效率从小到大依次为结构 A、结构 B、结构 C、结构 D；粒径为 5 µm 颗粒时，分级效率依次为结构 A 为 36.3%，结构 B 为 58%，结构 C 为 63.8%，结构 D 为 84.2%；粒径为 15 µm 颗粒时，分级效率依次为结构 A 为 70.3%，结构 B 为 81.1%，结构 C 为 89.9%，结构 D为 100%。由此可见，蜗壳半径的增加对分离效率有明显的提高，特别是对于粒径较小的颗粒。

图9 不同蜗壳半径下，旋风分离器的分级效率Fig.9 Separation efficiency of cyclone separator at various radius of volute

图10 所示为旋风分离器不同蜗壳半径对进出口压差影响。由图 10 可知，旋风分离器蜗壳半径增加，进出口的压差增加；当蜗壳半径为 4 420 mm 时，压差显著增加。其他结构参数不变，旋风分离器蜗壳半径增加，旋风分离器内气体体积增大，气流与壁面接触面积增大，此时压差增高，系统阻力增大，系统能耗升高。

图10 不同蜗壳半径下进出口压差Fig.10 Pressure difference between inlet and outlet at various radius of volute

由上述分析可知，旋风分离器的蜗壳半径越大，分离效率越高，但同时压差增大，导致系统能耗也增大。在实际生产中，对于粒径大于 25 µm 颗粒，选择直切式旋风分离器，分离效率高，制造成本低，能耗低；对于粒径小于 25 µm 颗粒，选择蜗壳式旋风分离器，鉴于系统能耗，应选择合适的蜗壳半径。

3 结论

本文采用 RNGk-ε模型以及 DPM 模型，对 4 种结构的旋风分离器内流场进行数值模拟，并以分离效率与压差为评价指标，探究旋风分离器蜗壳半径对物料分离性能的影响，得到以下结论。

(1) 蜗壳半径对旋风分离器速度场和静压有一定的影响。其他结构参数不变，旋风分离器蜗壳半径增大，筒体内流场速度增大，壁面处静压增大，因而颗粒受到离心力增大，减少了颗粒短路，进而提高物料分离效率。

(2) 旋风分离器蜗壳半径越大，物料分离性能越好。粒径为 5 µm 颗粒时，旋风分离器的分级效率依次为结构 A 为 36.3%，结构 B 为 58%，结构 C 为 63.8%，结构 D 为 84.2%；粒径为 15 µm 颗粒时，旋风分离器的分级效率依次为结构 A 为 70.3%，结构 B 为 81.1%，结构 C 为 89.9%，结构 D 为 100%。

(3) 旋风分离器蜗壳半径越大，进出口压差越大。其他结构参数不变，旋风分离器蜗壳半径增加，旋风分离器内气体体积增大，气流与壁面接触面积增大，此时压差增高，系统阻力增大，系统能耗升高。