学情前测：精准把握单元整合的有效手段——以人教版数学教材三年级下册“两位数乘两位数”单元教学为例

于 飞

（浙江省海宁市南苑小学）

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）中提出要重视单元整体教学设计，并指出：“单元整体教学设计要整体分析数学内容本质和学生认知规律，合理整合教学内容，分析主题—单元—课时的数学知识和核心素养主要表现，确定单元教学目标，并落实到教学活动各个环节，整体设计,分步实施，促进学生对数学教学内容的整体理解与把握，逐步培养学生的核心素养。”“前测”是教学前为了准确把握学情，教师设计有针对性的评测题，对学生进行测试，然后根据测试数据，提出相应的教学改进策略，做到以学定教。那么，前测“前”，教师应该思考什么？前测“题”，应该如何定位目标？前测“数据”，应该反映什么问题？前测“后”，应该如何进行教学改进？笔者以人教版数学教材三年级下册第四单元“两位数乘两位数”单元教学为例做一些探讨。

一、思单元整体

（一）整体分析——关键期与转折点

“两位数乘两位数”是整数乘法学习的关键期和转折点，它是学生在二年级上册学习了表内乘法，三年级下册学习了多位数乘一位数的基础上教学的，也是为四年级上册学习三位数乘两位数做笔算表征知识的准备。笔算竖式表征从多位数乘一位数“一层”跨越到两位数乘两位数“两层”，是竖式表征形式上的一次飞跃，但运算的算理和算法又是相通的，原理都是“拆分”。“两层”竖式掌握了，四年级上册的三位数乘两位数，以及更多层数的笔算，学生就能自主迁移了。

（二）单元分析——小步走与析学情

笔者发现，人教版教材的编排步子较小，本单元的学习重点是理解和掌握两位数乘两位数的笔算乘法算理和算法。而“口算乘法”安排3课时，为笔算乘法所做的铺垫为：两位数乘一位数关联乘法竖式第一层，两位数乘整十数关联第二层，内容划分过细，忽略了真实学情（如表1）。

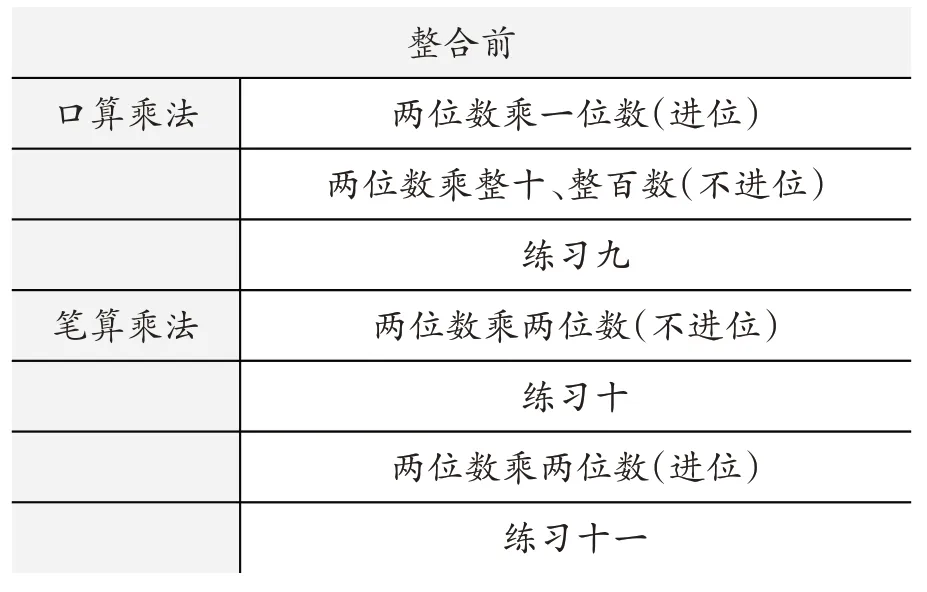
表1 “两位数乘两位数”单元计算内容编排

基于以上单元整体分析，笔者设想整合这一单元口算乘法“两位数乘一位数”“两位数乘整十数”和笔算乘法“两位数乘两位数”（不进位）”为1课时，将口算乘法中的“拆分”融于竖式计算中，充分展开“拆分”的教学，沟通联系竖式，理解每一步的含义，最后拓展到四年级上册“三位数乘两位数”，以提高学生的迁移能力。

二、定前测目标

为了准确把握学情，通过思考第1课时能否基于单元整体分析进行有效的内容整合，笔者拟定了如下前测题（“两位数乘两位数”前测单）。

1.直接写得数：

2.用你想到的或者喜欢的方法，计算出14×12的得数，写出必要过程。

3.列竖式计算（学生没学过，有挑战）：12×44=48×37=

前测目标为：

第1题，题目选自教材第41~42页例题及“做一做”，意在检测学生对两位数乘一位数和两位数乘整十、整百数的掌握情况，即口算乘法，少教，甚至不教，是否可行？

第2题，题目选自教材第46页例题，但不限定方法，用自己喜欢或者想到的方法，算出得数。检测学生是否能用“拆分”的方法，将新知转化为旧知，即拆分，学生会吗？

第3题，题目选自教材第47页练习题及第49页例题，限定方法，只能用竖式计算。检测第2题学生采用“拆分”的方法，第3题能否成功列出“两层”竖式以及进位乘法对学生影响有多大，即会拆分与会竖式之间有多大距离？

以上3题的前测目标，均围绕预设的单元整体设想，采集有针对性的数据和典型案例。

三、析数据价值

为保证样本数据的真实性和代表性，笔者选取了本校4位教师任教的4个不同班级共178名学生进行了前测，数据如表2、表3和表4。

表2 学生对口算乘法的掌握情况汇总

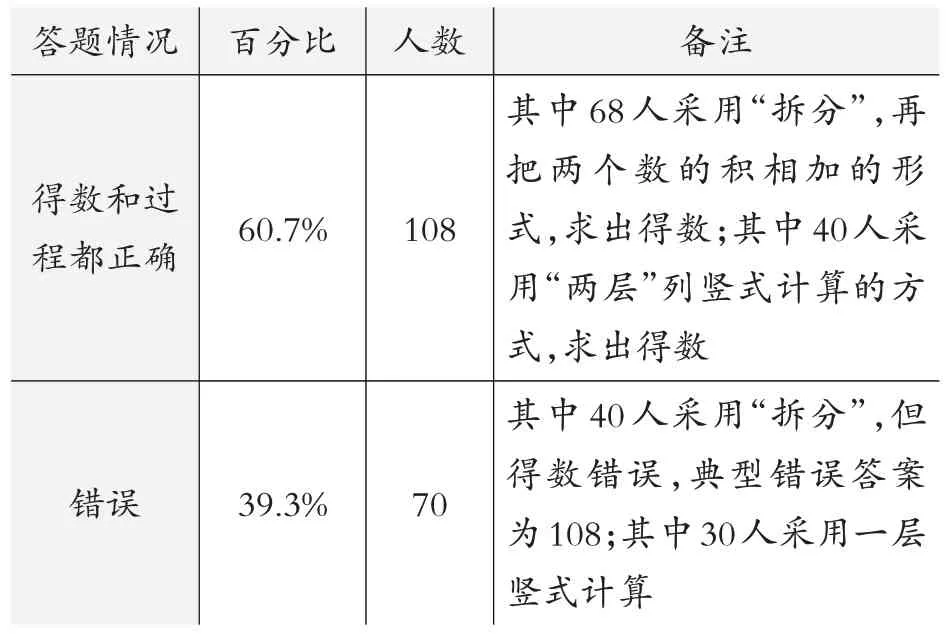
表3 学生对笔算乘法（不进位）掌握情况（不限定方法）汇总

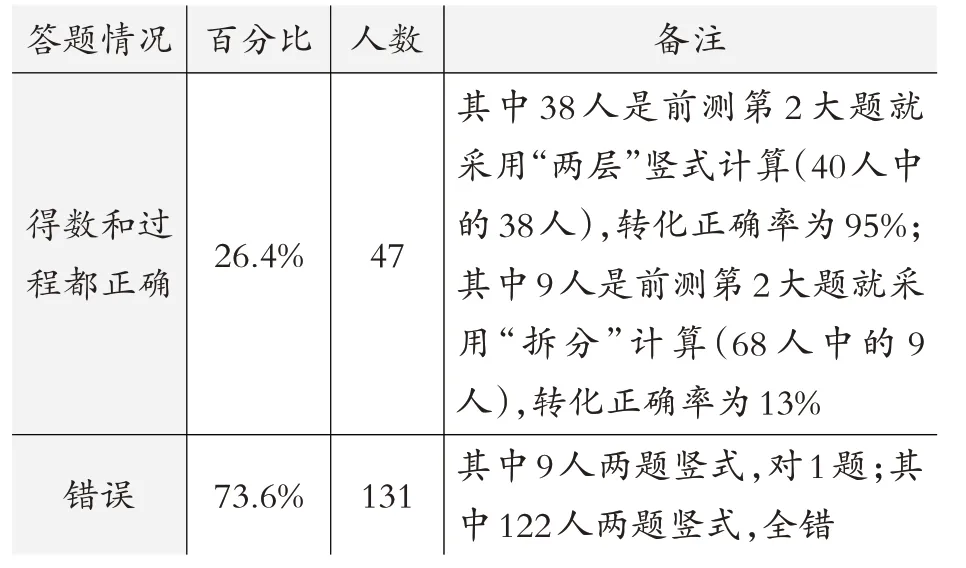
表4 学生对笔算乘法（不进位、进位）掌握情况（限定方法）汇总

（一）口算乘法要少教

表2数据反映：

1.超过一半的学生对两位数乘一位数的口算掌握得很好，该知识点因此可以不作为完整一课时单独教学。

2.学生对两位数乘整十数、整百数的口算，还存在一定问题，需要关注学生在口算时对“拆分”和末尾添0的理解和熟练运用。

表3数据反映：超过60%的学生在不限定方法时，能通过自主尝试求出14×12的积，并且有合理的过程。这其中采用“拆分”且计算正确的人数占到正确总人数的68.5%，说明学生对于“拆分”的原理已经有了较强的理解，能够运用此方法将新知转化成旧知。不管是正确的还是错误的，采用“竖式”计算的学生人数都比采用“拆分”的人数少很多。

表4数据反映：限定竖式计算，正确率比不限定下降明显，仅有26.4%的学生两题竖式计算正确，而做对的47人中的38人，还是前测第2大题也采用“两层”竖式计算的学生，正确转化率高达95%。但是，仅有9位学生能从第2大题时的拆分转化到竖式计算，并正确，正确转化率仅有13%。这表明“会拆分”与“会竖式”之间看似是一层窗户纸，实则犹如一条鸿沟难以跨越。两题全对47人，做对1题9人，这表明“进位乘法”对于已经掌握两层竖式的学生而言，并没有太大挑战。表内乘法的难点不在于进位，而是从“一层”到“两层”这中间的飞跃。

基于以上3道前测题的目标设定，以及相关数据分析，笔者得到了如下4条教学启示：一是减少甚至取消口算作为完整一课时的节数，但要关注两位数乘整十数的口算，可以通过拆分和末尾添0熟练计算；二是增加拆分方法与直观图形“形、式”的沟通，充分理解算理算法，在会拆分与会竖式的鸿沟之间，架起沟通的桥梁；三是整合两位数乘两位数与三位数乘两位数笔算，沟通联系；四是弱化进位笔算，不作为完整一课时教学，引入拓展课。

因此，本单元两位数乘两位数计算部分，笔者对课时内容划分作如表5调整。

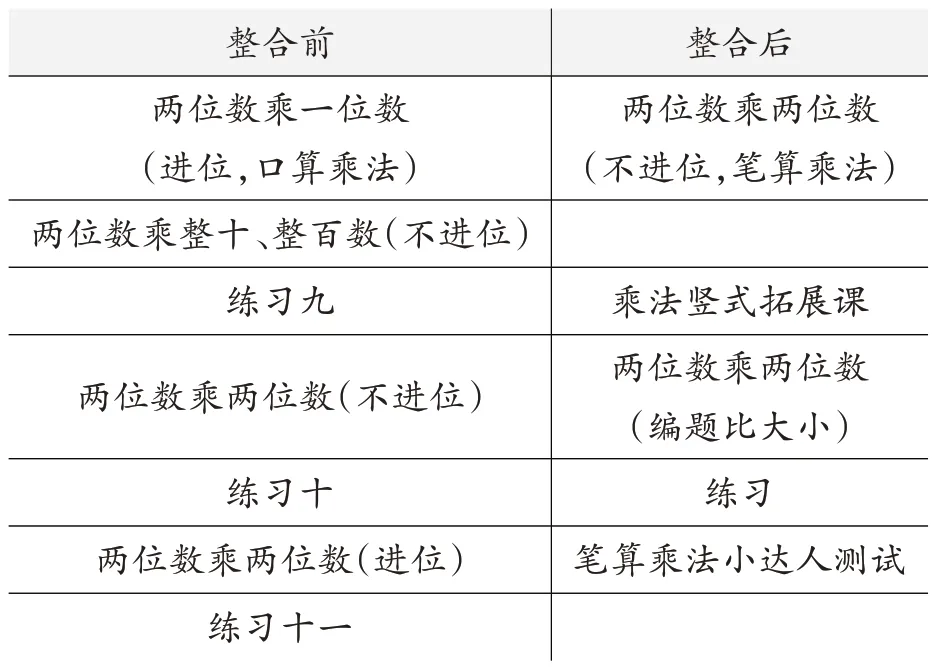
表5 “两位数乘两位数”单元计算内容编排

四、促理法迁移

笔者将本课整合为一节新课：两位数乘两位数（不进位），进行了如下教学设计。

（一）口算引入，强化口算过程，为笔算乘法做铺垫

根据前测第1题的数据反映，学生对于口算乘法总体已经有较强的基础，特别是两位数乘一位数。虽然两位数乘整十、整百数有一定错误率，但仔细分析，其实质主要还是在于如何“拆分”以及末尾添0。因此，在口算引入环节，主要是让学生表达清楚是怎么口算的，无论是拆分的方法，还是末尾添0，要让学生充分表达，为笔算乘法做知识上的铺垫。

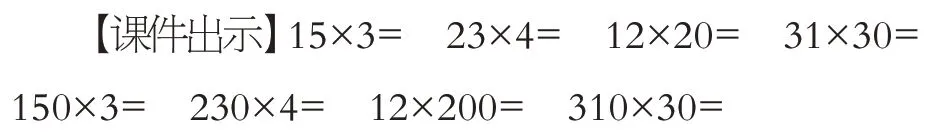
【要求】课件逐一闪现每题，让学生说一说是怎么口算的。主要关注最后两组题目学生的说理过程。

（二）自主尝试，沟通“拆分”与“竖式”间的联系

笔算两位数乘两位数的原理是“拆分”，两层竖式只是一种比较合理、简洁的表征方式。因此，教学重点不是用怎样的竖式计算，因为对于从来没有见过两层竖式的学生而言，要其自主“创造”出两层，这是极其有挑战的，而那些已经会用两层竖式计算的学生，也都是课外提前知道了有两层竖式。所以，沟通“拆分”与“竖式”之间的联系，使学生理解每一步的含义，才是教学的真正重点。

【课件出示】每套书有14本，王老师买了12套。一共买了多少本？

【要求】（1）自主尝试，用自己喜欢或者想到的方法，写出完整过程，算一算；（2）小组交流，结合点子图，圈一圈，画一画，说说你是怎么算的？（3）投影典型计算方法（如图1），问学生看懂了哪种方法，分享交流。

图1

1.理解拆分

生：第一幅图是把12拆成10+2，10个14+2个14，140+28=168。

生：第二幅图是把14进行了拆分，分成了10和4,10个12+4个12，等于120+48=168。

生：第三幅图是把12拆成了9和3，因为14×9，14×3，两位数乘一位数是可以口算的，126+42=168。

师：虽然它们看上去都有点不一样，但本质都是相同的，你知道是什么？

生：都用到了拆分的方法，把其中一个两位数拆分成两个一位数，或者是一个10，一个一位数。都可以进行口算。

2.沟通竖式

师：有一位同学是这样做的（如图2），你能看懂吗？

图2

生：它用的是竖式计算。

师：这个竖式和我们以前学的有什么不一样？又和刚才的拆分方法有什么联系？

生：它是两层的竖式，我们以前学的是一层的竖式。12的2先和14相乘得到28，然后12的10和14相乘得到140，最后相加得168。

师：这位同学的竖式，其实和哪位同学的拆分是一样的？

生：和图1中的第二幅图是一样的，都是把12拆成10和2，分别和14相乘，最后相加。

师：是的，用第二个因数12中的每个数分别与第一个因数14相乘，最后把两个积28和140相加，得到最后的结果168。那为什么两位数乘两位数的竖式要两层呢？而以前的竖式只有一层。

生：因为以前多位数乘一位数，第二个因数只有一个数字，只需要计算1次，而现在第二个因数是两位数，拆分后要计算两次，所以是两层。

生：如果14×12也用一层竖式的话，和拆分的方法就对应不起来了，一层要计算两个不同的算式，容易出错。

（三）学会迁移，类推三位数乘两位数，探理法相通

两位数乘两位数是整数乘法的关键期和转折点，学生理解和掌握了，有助于迁移类推到三位数乘两位数，因为二者在算法和算理上是相通的，竖式的表征形式也都是两层。因此，在本课时教学中，可以作为拓展部分，让学生根据今天所学知识延伸拓展探究三位数乘两位数的笔算。通过4个大问题，检测学生迁移能力。

【问题1】两位数乘两位数的笔算是两层的竖式，那三位数乘两位数，你知道竖式会是几层吗？先想一想。

生：3层。

生：还是2层。

【问题2】到底三位数乘两位数竖式是几层？算一算123×21，验证你的猜想。

（学生独立尝试竖式计算123×21，一位学生在黑板上板书：两层）

【问题3】竖式计算时跟这位同学一样，也是两层的请举手，为什么还是两层？

生：因为都是用下面的因数去乘上面的因数，21的1去乘123得到第一层123，21的20去乘123得到第二层2460。方法和14×12是一样的。

【问题4】三位数乘两位数要到四年级上册才学习，为什么你们现在就会了？

生：因为三位数乘两位数的计算方法和今天学习的两位数乘两位数方法是一样的，都是拆分第二个因数，然后分别和第一个因数相乘，最后加起来。

以上是我们基于前测实证研究“两位数乘两位数”单元整合思路与第1课时实践，阐述了如何基于单元整体分析，研制有针对性的前测题，再结合数据分析，进行单元整合教学。在本课中展现的数据实证研究为优化单元整体结构、促进理法的深度迁移提供了重要的方向支撑。