一类三维三次系统极限环的新下界
刘桔坤,黄文韬,刘宏普
(1.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004;2. 广西师范大学 数学与统计学院,广西 桂林 541006)
极限环问题是微分方程定性理论中非常重要的热点领域。1900年巴黎世界数学家大会,德国数学家Hilber提出著名的23个数学难题,其中第16个问题的后半部分就是寻求n次实平面微分自治系统极限环数目的最小上界以及这些极限环的相对位置。这一问题吸引了众多学者关注,也取得了很多优秀研究成果。然而这个问题的解决非常困难,即使n=2的情形仍没有得到解决。近几十年来,寻求平面系统能产生极限环个数的最大下界问题有很多研究成果[1-6]。近年来,三维系统的研究也取得了一些研究成果,如文献[7]构造一类具有3个极限环的三维Lotka-Volterra竞争系统;文献[8]研究一类三维n(n>1)次系统,并且证明这类系统至少存在n2个极限环;文献[9]证明三维二次系统在单个奇点周围至少存在7个极限环;随后文献[10]将这个结果改进至10个极限环;文献[11]研究一类具有2个对称奇点的三维二次系统,证明在这2个奇点周围至少存在10个极限环;文献[12]研究一类具有Z3对称的三维二次系统,证明在3个奇点周围存在具有(4,4,4)分布的12个极限环;文献[13]证明一类三维二次系统在2个对称奇点周围存在具有(6,6)分布的12个极限环。目前,关于三维三次系统极限环的结果相对较少,文献[14]提出一种三维微分系统奇点量的递推算法,并采用该算法研究一类三维三次系统,得到系统可分支出5个极限环;文献[15]证明一类三维三次Kolmogorov系统在正平衡点(1,1,1)处可分支出5个小振幅极限环;文献[16]将这个结果改进至7个极限环;文献[17]研究一类三维三次ELS(extended Lorenz system)系统,得到系统在3个孤立的平衡点处各存在1个极限环。
本文研究如下一类三维实系统的极限环分支问题:
(1)
证明系统(1)有16个极限环,得到三维三次系统极限环个数的一个新下界。
1 预备知识
先叙述需要的一些知识(详见文献[14])。考虑以下三维实系统:
(2)
式中x、y、u、d、t、Ajkl、Bjkl、djkl∈R,k、j、l∈N。
对系统(2),存在中心流形u=u(x,y),可表示为如下关于x和y的多项式级数
u=u(x,y)=x2+y2+h.o.t.,
式中h.o.t.为高阶项。
引入变换
系统(2)可化为如下系统:
(3)
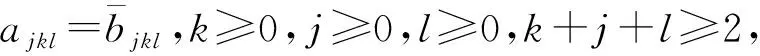
引理1[14]对系统(3),令c110=1,c101=c011=c200=c020=0,ckk0=0,k=2,3,…那么可以唯一地逐项确定如下形式级数
使得
式中μm是系统(3)在原点的第m个奇点量。当α≠β或α=β,γ≠0时,cαβγ可由以下递推公式确定,
对每一个正整数m,μm可由下面递推公式确定,
当α<0或β<0或γ<0或γ=0,α=β时,有cα,β,γ=0。
引理2[14]对任意正整数k,系统(2)的第k个焦点量v2k+1(2π)和系统(3)的第k个奇点量μk满足等价关系v2k+1(2π)~iπμk。
引理3[11]对系统(2),若在条件c*下原点是一个n阶细焦点,并且
那么系统(2)的原点可以分支出n个极限环。
2 主要结果
易知系统(1)关于平面XOU对称,且有2个对称奇点(0,1,1)、(0,-1,1)。由对称性,仅就奇点(0,1,1)讨论。引入平移变换x1=x,y1=y-1,u1=u-1,代入系统(1)得到如下系统:
(4)
相应地,系统(1)的平衡点(0,1,1)变成系统(4)的原点。
再通过变换z=x1+iy1,w=x1-iy1,u2=u1,T=it,系统(4)化为如下系统(5)
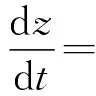
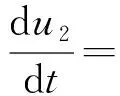
由引理1,借助计算机代数软件,计算系统(5)原点的奇点量,得到定理1。
定理1系统(5)原点的前8阶奇点量为
情形1 若c17=0,则
μ3=μ4=μ5=μ6=μ7=μ8=0。

式中:
F1=-20 960-576 495c17+22 218a3c17-886 144a5c17-93 564b16c17-289 340c17c3,
F2=38 913 088+11 225 789 614c17+9 850 427 480a5c17+263 071 844 256c172+30 728 488 635b16c172+
627 334 964 750a5c172+315 624 818 600a52c172+27 345 269 250a5b16c172+29 178 720b16c17+
4 066 298 620c17c3+205 262 417 620c172c3+214 392 807 200a5c172c3+7 975 989 450b16c172c3+
36 147 246 200c172c32,
F3=-355 974 829 793 661 101 632+3 315 404 756 119 259 258 420c17c3-
22 390 970 288 312 684 331 000c172c32+1 145 662 044 538 954 645 920b16c17-
820 755 201 041 988 537 461 194c172+570 839 670 037 146 542 404 485b16c172+
9 631 555 088 136 199 494 150a5b16c172-118 062 559 688 188 506 600 914 250a5c173-
1 956 711 824 169 040 245 100 950b16c173+718 703 192 174 636 311 387 875b162c173-
678 082 272 715 194 958 520a5c17+214 355 485 871 217 085 122 000a5c172c3+
2 801 127 021 628 092 489 150b16c172c3-8 775 317 955 632 496 616 530 000a5c173c3+
2 751 250 117 933 061 595 454 500b16c173c3-2 728 460 204 692 456 931 190 000c173c32+
8 028 915 274 201 903 177 824 000a5b16c173-41 651 961 992 469 620 963 242 500c173c3-
70 972 031 251 036 267 236 617 850c173+758 798 200 400 096 777 877 020c172c3+
3 040 820 285 709 409 899 908 800a5c172+74 021 654 281 639 387 262 314c17,
F4、F5、F6分别是关于a3、a5、b16、c3、c17的6次、8次、9次多项式,且其项数分别为40、80、139,详情可通过链接https:∥pan.baidu.com/s/1f9eWxoNgMcBJJSoc5sDt4Q(提取码:hfun)查看。在计算每个μk时,已令μk-1=0,k=2,…,8。
定理2系统(5)的前8阶奇点量为0当且仅当a17=c17=0。
证明首先证明充分性。将a17=0,c17=0代入定理1的前8个奇点量的表达式,显然有μ1=μ2=μ3=μ4=μ5=μ6=μ7=μ8=0。

GroebnerBasis [{F1,F2,F3,F4,F5,F6},{a3,a5,b16,c3,c17}]={1},
即F1=F2=F3=F4=F5=F6=0没有公共根。因此在情形2下,系统(5)的前8个奇点量不可能同时为零。综上,定理2得证。
定理3对系统(4),当a17=0,c17=0时,曲面Γ:u1=0是一个不变代数曲面,它定义了一个全局中心流形,并且在该中心流形上,原点是系统的中心(即系统(1)的奇点(0,1,1)、(0,-1,1)为a17=0,c17=0时的中心)。
证明若a17=0,c17=0,则系统(4)化简为:
(6)
由文献[13]可知,对如下系统
(7)
式中:P(x1,y1,u1)、Q(x1,y1,u1)、R(x1,y1,u1)的次数均不超过k,多项式方程F(x1,y1,u1)=0为系统(7)的不变代数曲面当且仅当
(8)

首先从l=1开始搜索,证明F(x1,y1,u1)的存在性。对l=1,令F(x1,y1,u1)=ax1+by1+cu1,将F(x1,y1,u1)以及余因子K(x1,y1,u1)代入式(8),比较同次幂系数,可得到下面代数方程组:
-ah4=0, -bh4-ah7=0, -aa4-ch4-ah8=0, -ah5-bh7=0, -a-bh0=0,b-bh1-ah2=0,
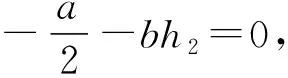

解以上代数方程组得到a=0,b=0,c=1,故Dardoux多项式F(x1,y1,u1)=u1,因此曲面Γ:u1=0为系统(6)的一个不变代数曲面。下面证明曲面Γ:u1=0是系统(6)的一个中心流形。首先,计算函数F(x1,y1,u1)=u1在原点的梯度,也就是曲面Γ:u1=0在原点的法向量,得到F(0,0,0)=(0,0,1)。又由于中心流形在原点处的切空间是由e1=(0,-1,0),e2=(1,0,0)这2个向量张成的,而F(0,0,0)·e1=0,F(0,0,0)·e2=0。因此,曲面Γ:u1=0是系统(6)的一个中心流形,即可停止对Fl(l≥2)的搜索。最后,需要证明在中心流形Γ:u1=0上,系统(6)的原点是中心。当u1=0时,系统(6)化简为如下系统
(9)
易知系统(9)关于y轴对称,由对称原理[18]可知系统(9)的原点是一个中心。综上,定理3得证。
接下来讨论系统(1)从奇点(0,1,1)分支的极限环的最大数目。首先考虑系统(5)原点的细奇点阶数。由定理1和定理2可得以下定理4。
定理4系统(5)的原点是8阶细奇点当且仅当下列条件满足
(10)
借助计算机代数软件,得到满足F1=F2=F3=F4=F5=0的16组实数解,其中一组解为
(11)
通过计算,
由引理3可得以下结果。
定理5对系统(1),当系数满足条件(10)时,奇点(0,1,1)为8阶细焦点,并且系统(1)参数经过合适的扰动,在奇点(0,1,1)处可分支出8个极限环。因此,系统(1)在2个奇点(0,1,1)和(0,-1,1)附近存在16个极限环,呈8-8分布。
3 结语
本文研究一类三维三次系统的中心和极限环分支问题。通过符号计算和数值计算,得到系统2个对称奇点(0,1,1)、(0,-1,1)成为中心的一组充要条件,并导出这2个奇点同时成为8阶细焦点的条件,进而证明系统至少存在16个小振幅极限环。据作者所知,这是目前三维三次系统关于极限环个数的最好结果。

