车联网中网络切片资源分配方案*

李 悦，任春莉，章国安

(南通大学 信息科学技术学院，江苏 南通226019)

0 引 言

作为第五代移动通信关键技术之一，网络切片技术旨在对现有物理网络进行划分，形成多个独立的逻辑网络，为差异化业务提供定制化的服务。5G商用促进了车联网的快速发展，带来了更多的车联网业务，包括交通安全类业务和信息娱乐类业务，从而导致了多样化的服务质量(Quality of Service,QoS)要求[1]。因此，将网络切片技术引入车联网，可以更好地支持不同的车联网应用案例。

目前，已经有很多工作对网络切片及资源分配问题进行了研究。文献[2]考虑两种5G通用业务，提出了一种基于离线强化学习和低复杂度启发式算法的随机切片方案，在可达数据速率和时延等方面提升了网络性能。文献[3]利用聚类算法对高相似度的车联网业务进行聚类并映射到相应切片中，提出了共享比例公平的切片调度方案，在平均比特传输时延方面比静态方案具有更高的性能。文献[4]为通信服务提供商(Communication Service Provider,CSP)提出了一种新的“切片即服务”框架，考虑租户的切片请求对CSP的网络的影响，提出了一种联合准入控制机制。文献[5]考虑车辆应用的优先级，提出了一种基于替代凹搜索算法的带宽预留和切片分配方案，在网络资源利用率方面优于传统的切片分配方案。考虑到异构云无线接入网中存在前向链路受限的问题，文献[6]提出了一种基于干扰阈值的设备到设备多用户分簇方案，通过联合优化信道和功率资源，有效提高了系统频谱利用率。文献[7]考虑无线设备电池容量的限制，在保证QoS要求的前提下，研究无线功率后向散射通信网络中联合计算卸载和无线资源分配问题，提出了一种基于迭代的资源分配算法，有效降低了系统总能耗。文献[8]则对5G异构网络的定义及不同场景进行了介绍，并对5G异构网络中的资源分配算法进行了全面的调查总结，讨论了现有挑战及未来的研究趋势。

考虑通信流量到达的随机性，引入缓冲队列模型，文献[9]研究了不同无线服务总成本最小化问题，提出了长时间尺度的带宽切片算法，以及短时间尺度的设备调度、功率控制和视频质量决策，降低了服务成本，提高了时延性能。文献[10]考虑多种服务的QoS要求，提出了一种联合资源分配和功率控制的在线网络切片调度策略，与不考虑部分约束条件的方案相比，提高了系统的时延性能。文献[11]应用基于网络切片的聚类算法将车辆划分为多个逻辑网络，提出了一种联合视频质量选择和资源分配技术，确保了更高的视频质量体验。

上述文献虽然考虑了流量到达的随机性，却忽略了当数据到达量过大时通信链路数据队列过长而导致网络拥塞的情况。因此，本文在将车联网划分为安全服务切片和信息娱乐服务切片的基础上，考虑信息娱乐服务切片的随机数据量到达过大的情况，对接入的数据量进行控制，在保证各切片QoS要求的前提下，以最大化信息娱乐服务切片的平均和吞吐量为目标，提出一种功率控制和资源分配方案。

1 系统模型与问题建模

1.1 系统模型

本文考虑如图1所示的车联网场景，由基站(Base Station，BS)和道路车辆构成。设定的车辆通信网络被划分为两个网络切片，分别用切片1和切片2表示。其中，切片1为车辆提供交通安全类业务，此类业务要求低时延和高可靠性，切片1中的车辆采用车辆到车辆(Vehicle to Vehicle,V2V)通信方式；切片2为车辆提供车载信息娱乐类业务，要求高传输速率，切片2中的车辆采用车辆到基础设施(Vehicle to Infrastructure,V2I)通信方式。

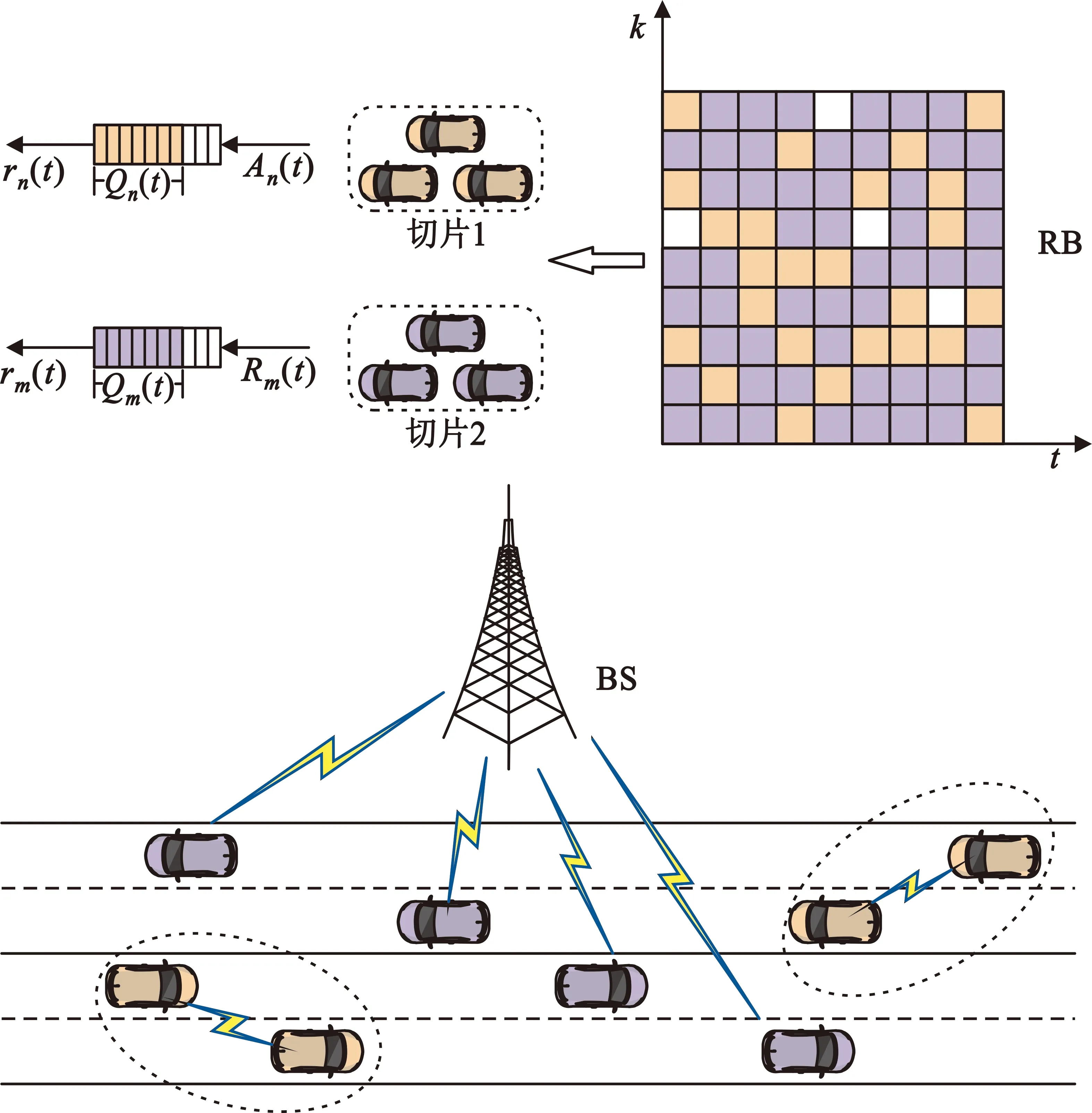
图1 系统模型

令n∈N表示切片1所服务的V2V车辆对，其中N={1,2,…,N}是对应所有V2V车辆对的集合。令m∈M表示切片2所服务的车辆，其中M={1,2,…,M}是对应所有车辆的集合。令k∈K表示网络中的资源块(Resource Block,RB)，其中K={1,2,…,K}是所有RB的集合，每个RB的带宽为B0。考虑系统以时隙的模式运行，每个时隙t∈{0,1,2,…,T-1}的持续时间为τ。二元变量an,k(t)∈{0,1}和am,k(t)∈{0,1}为网络中RB的分配指示符。若第k个RB在时隙t上分配给第n个V2V车辆对，则an,k(t)=1，否则an,k(t)=0。am,k(t)与之同理。为了保证切片之间相互隔离，两个切片不能同时使用同一个RB。设定的网络利用正交频分多址接入(Orthogonal Frequency Division Multiple Access,OFDMA)技术为车辆提供上行传输服务，每个切片中的RB相互正交，故资源分配约束如下式所示：

(1)

对于切片1和切片2中任意的V2V车辆对n和车辆m，它们的传输速率分别可以表示为

(2)

(3)

式中：pn,k(t)和pm,k(t)分别表示在时隙t上V2V车辆对n和车辆m在RB k上的发射功率；hn,k(t)和hm,k(t)则分别表示V2V车辆对n之间和车辆m到BS的传输信道增益；N0为噪声功率谱密度。为了保证切片2的最低速率rm,min要求，所有车辆m在时隙t上的传输速率需满足以下约束：

rm(t)≥rm,min。

(4)

考虑流量到达的随机性，分别为V2V车辆对n和车辆m构建队列模型，Qn(t)和Qm(t)表示队列长度。令An(t)和Am(t)分别表示V2V车辆对n和车辆m在时隙t的随机数据到达量，An(t)和Am(t)在不同时隙独立同分布，E{An(t)}=λn，E{Am(t)}=λm，λn和λm为平均数据到达量。令Rm(t)表示车辆m在时隙t上接入的数据量，则数据队列长度Qn(t)和Qm(t)的更新过程如下：

Qn(t+1)=max{Qn(t)-rn(t)τ,0}+An(t)，

(5)

Qm(t+1)=max{Qm(t)-rm(t)τ,0}+Rm(t)。

(6)

式中：Rm(t)在每个时隙t需满足0≤Rm(t)≤Am(t)。当所有V2V车辆对n和车辆m的队列都满足式(7)和式(8)的条件时，网络是稳定的[12]。

(7)

(8)

当网络稳定时，根据Little定理可知[13]，平均等待时延和平均队列长度成正比。对于V2V车辆对n而言，当数据队列长度超过阈值时数据将被丢弃，从而导致通信的不可靠问题。因此，切片1的时延和可靠性约束可以表述为[14]

(9)

式中：qn为队列长度阈值；ε为允许队列长度超过阈值的最大概率。

此外，当网络稳定时，平均和吞吐量可以由接入的数据量得到。因此，切片2的平均和吞吐量表示如下：

(10)

1.2 问题建模

令R={Rm(t),m∈M}表示切片2中所有车辆的接入数据量的向量，a={an,k(t),am,k(t),n∈N,m∈M,k∈K}和p={pn,k(t),pm,k(t),n∈N,m∈M,k∈K}分别表示RB分配和功率控制向量。为了最大化切片2的平均和吞吐量，构建随机优化问题的数学模型如下：

(11a)

(11b)

(11c)

(11d)

C4:rm(t)≥rm,min,∀m∈M;

(11e)

C5:0≤Rm(t)≤Am(t),∀m∈M;

(11f)

(11g)

(11h)

(11i)

C9:an,k(t),am,k(t)∈{0,1},∀m∈M,n∈N,k∈K。

(11j)

式中：Pn,max和Pm,max分别为V2V车辆对n和车辆m的最大发射功率；C1和C2保证了网络的稳定性；C3是切片1的时延和可靠性约束；C4使得车辆m的传输速率满足其最低速率要求；C5约束切片2的接入数据量，使其不超过到达的数据量；C6和C7分别限制V2V车辆对n和车辆m的发射功率不超过其功率阈值;C8和C9为RB分配约束。

2 问题转换与求解

2.1 问题转换

对于约束条件C3，可以借助Markov不等式来对其进行处理。

定义1如果X为非负随机变量且a>0，则Pr{X≥a}≤E[X]/a。

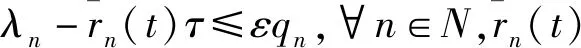
Hn(t+1)=max{Hn(t)+λn-εqn-rn(t)τ,0}。

(12)

令Θ(t)={Qn(t),Qm(t),Hn(t),n∈N,m∈M}表示实际队列和虚拟队列的向量，利用Lyapunov优化技术处理C1、C2和C3，则Lyapunov函数[12]的表达式定义如下：

(13)

L(Θ(t))表示队列拥塞程度，其越大则队列长度越大。Lyapunov偏移的表达式为

Δ(Θ(t))=E{L(Θ(t+1))-L(Θ(t))|Θ(t)}，

(14)

其表示一个时隙上Lyapunov函数的预期变化。因此，优化问题的偏移与加权代价函数定义如下：

(15)

式中：V≥0是引入的控制参数，表示与队列稳定性相比最大化切片2平均和吞吐量的重要程度。

引理1在时隙t，对于任意的队列状态和任意的分配策略，F(Θ(t))存在上限[12]，即

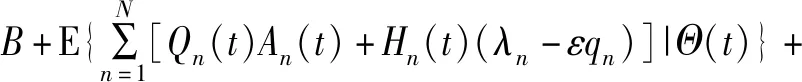
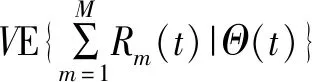
(16)

式中：B为有限常数。

根据Lyapunov优化理论，可以通过最小化F(Θ(t))的上限来获得良好的分配策略。因此，优化问题可以转换为

(17a)

s.t.C1:rm(t)≥rm,min,∀m∈M;

(17b)

C2:0≤Rm(t)≤Am(t),∀m∈M;

(17c)

(17d)

(17e)

(17f)

C6:an,k(t),am,k(t)∈{0,1},∀m∈M,n∈N,k∈K。

(17g)

2.2 问题求解

转换后的优化问题(17)可以分解为下面两个子问题。

(1)接入控制

(18a)

s.t.0≤Rm(t)≤Am(t),∀m∈M。

(18b)

问题(18)是一个简单的线性规划问题，具有以下最优解：

(19)

(2)RB分配与功率控制

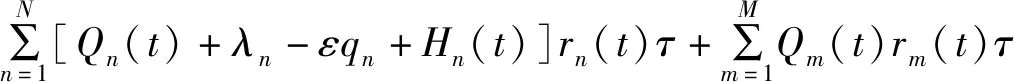
(20a)

(20b)

(20c)

(20d)

(20e)

C5:an,k(t),am,k(t)∈[0,1],∀n∈N,m∈M,k∈K。

(20f)

利用拉格朗日对偶分解对该优化问题进行求解。问题(20)的拉格朗日函数表达式如下：

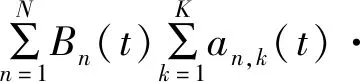
(21)

式中：λ、μ、θ为拉格朗日乘子向量。利用KKT条件[15]可得，当RBk分配给V2V对n或车辆m时，功率分配策略如下：

(22)

(23)

(24)

(25)

式中：

(26)

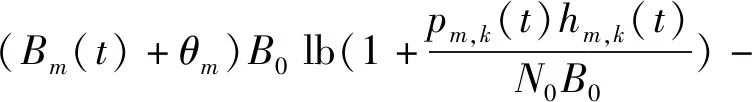
μmpm,k(t)。

(27)

根据两个子问题的求解，所提资源分配方案可用图2所示的流程图表示。

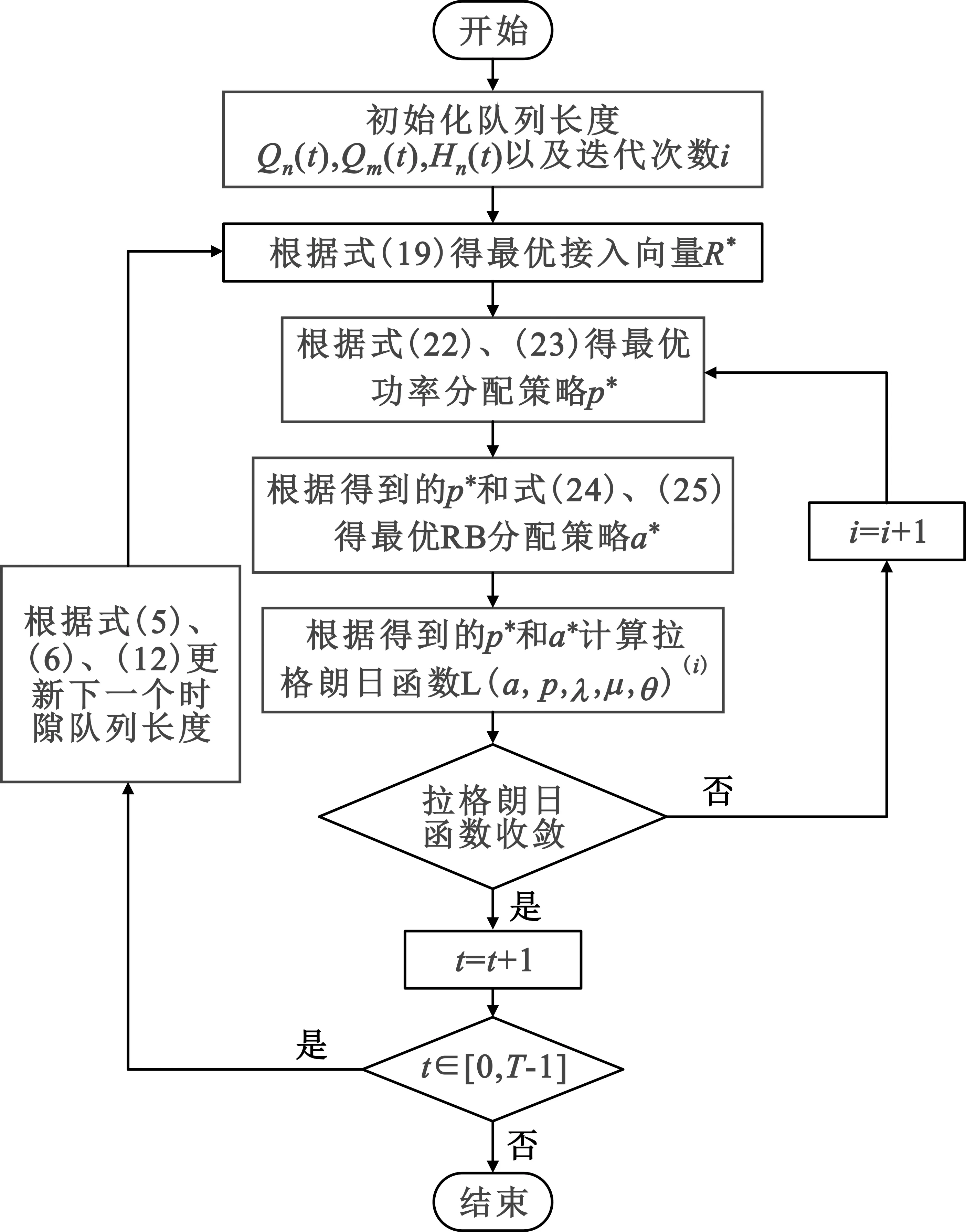
图2 所提资源分配方案流程图

3 仿真分析

本文使用Matlab仿真软件进行仿真分析，考虑高速公路应用场景，一条6车道高速公路穿过单个小区，小区半径为500 m，BS位于小区的中心。仿真参数参考文献[16-19]进行设置，参数汇总于表1。

表1 仿真参数设置

图3显示了平均队列长度Qavg与时隙t的关系。从图中可以看出，平均队列长度随着时隙的增加而增加，并逐渐趋于稳定。此外，更大的控制参数V将导致平均队列长度更大。这是因为V越大，表明最大化切片2的平均和吞吐量更加重要，从而致使队列长度更大。

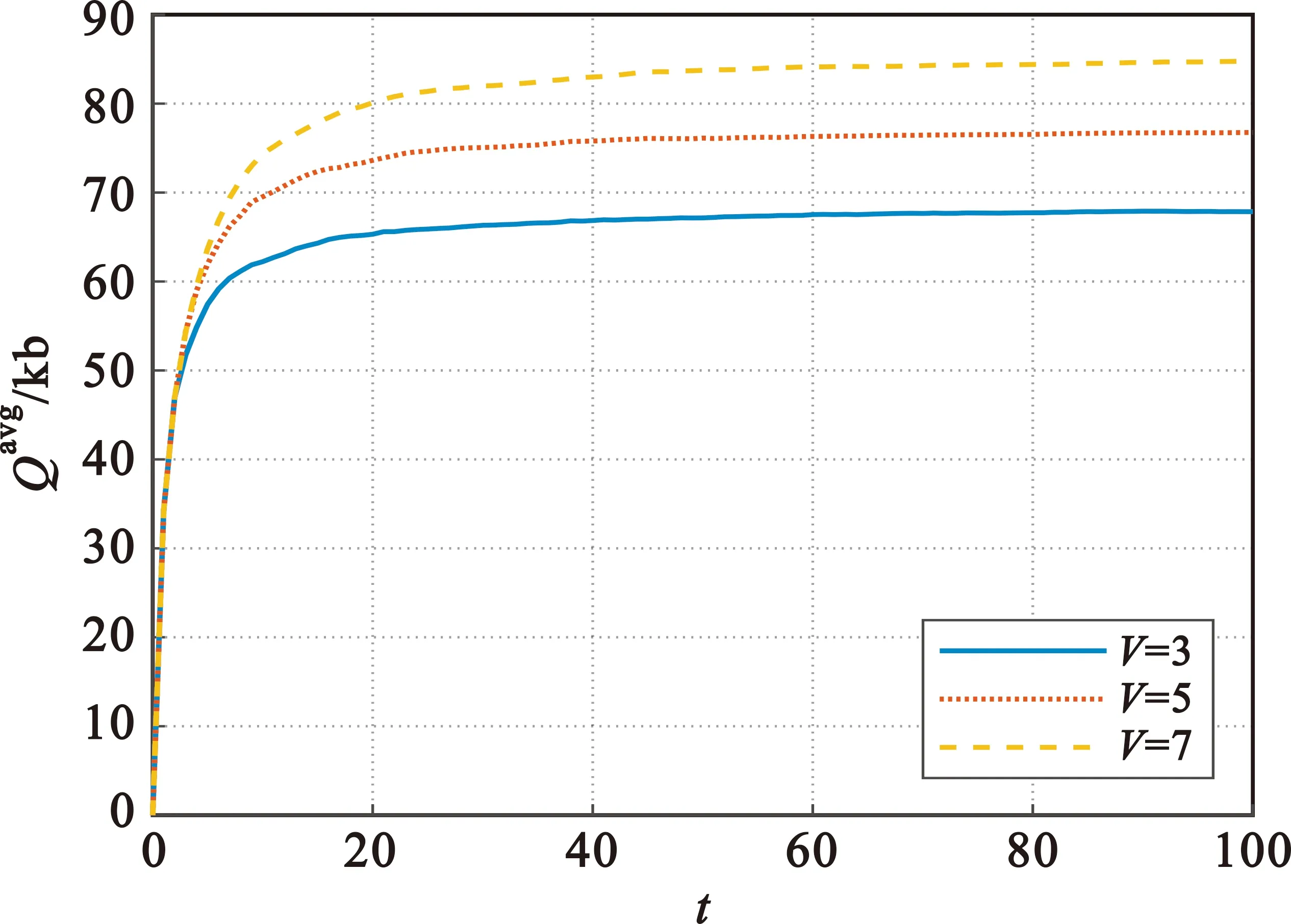
图3 平均队列长度与时隙t的关系

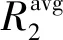
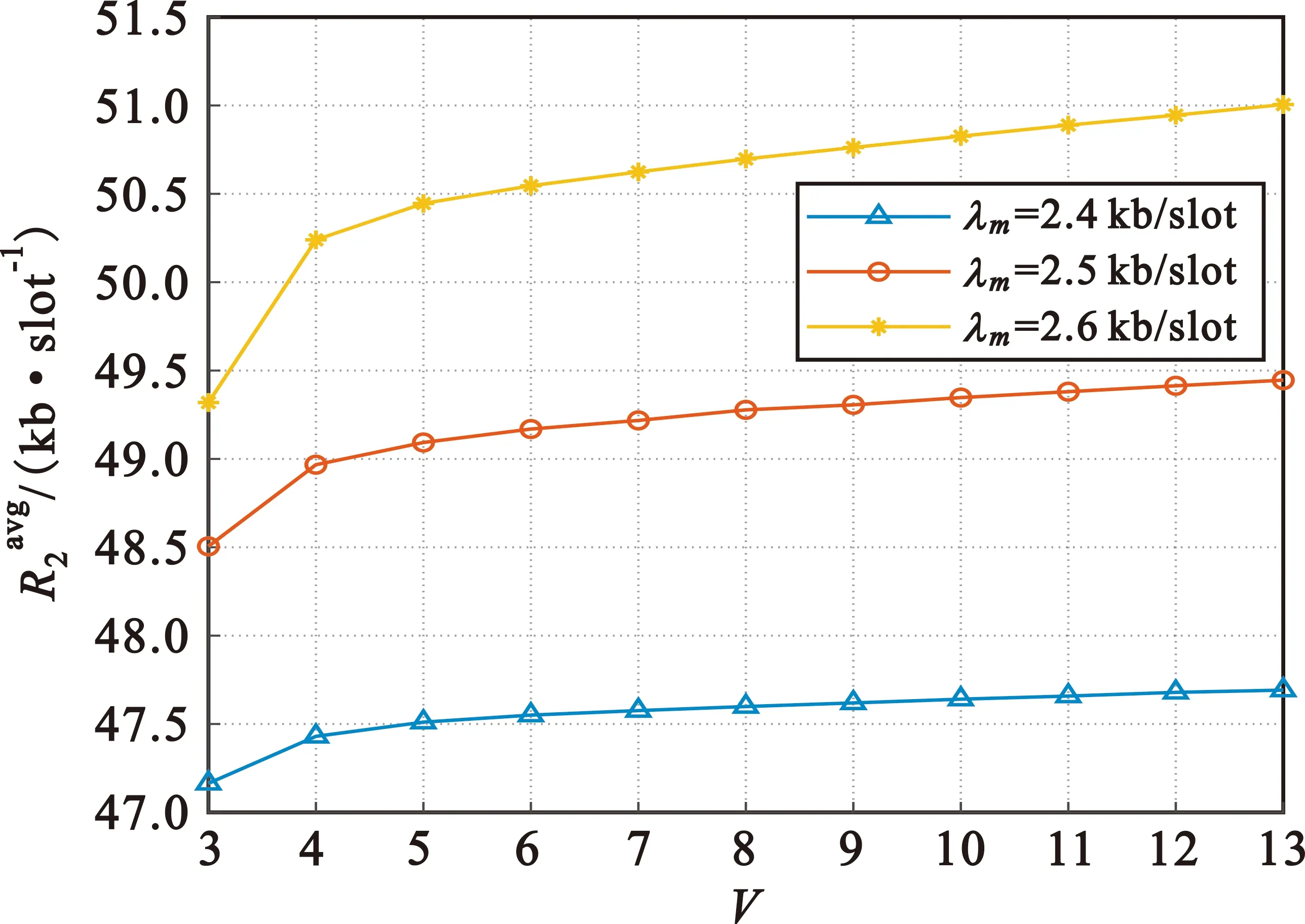
图4 平均和吞吐量与控制参数V的关系

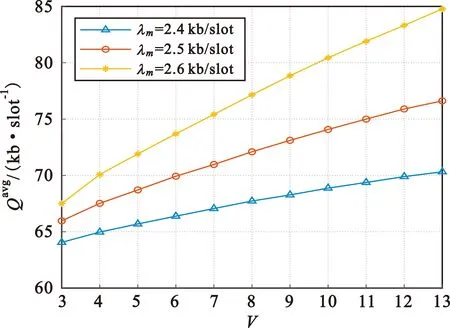
图5 平均队列长度与控制参数V的关系

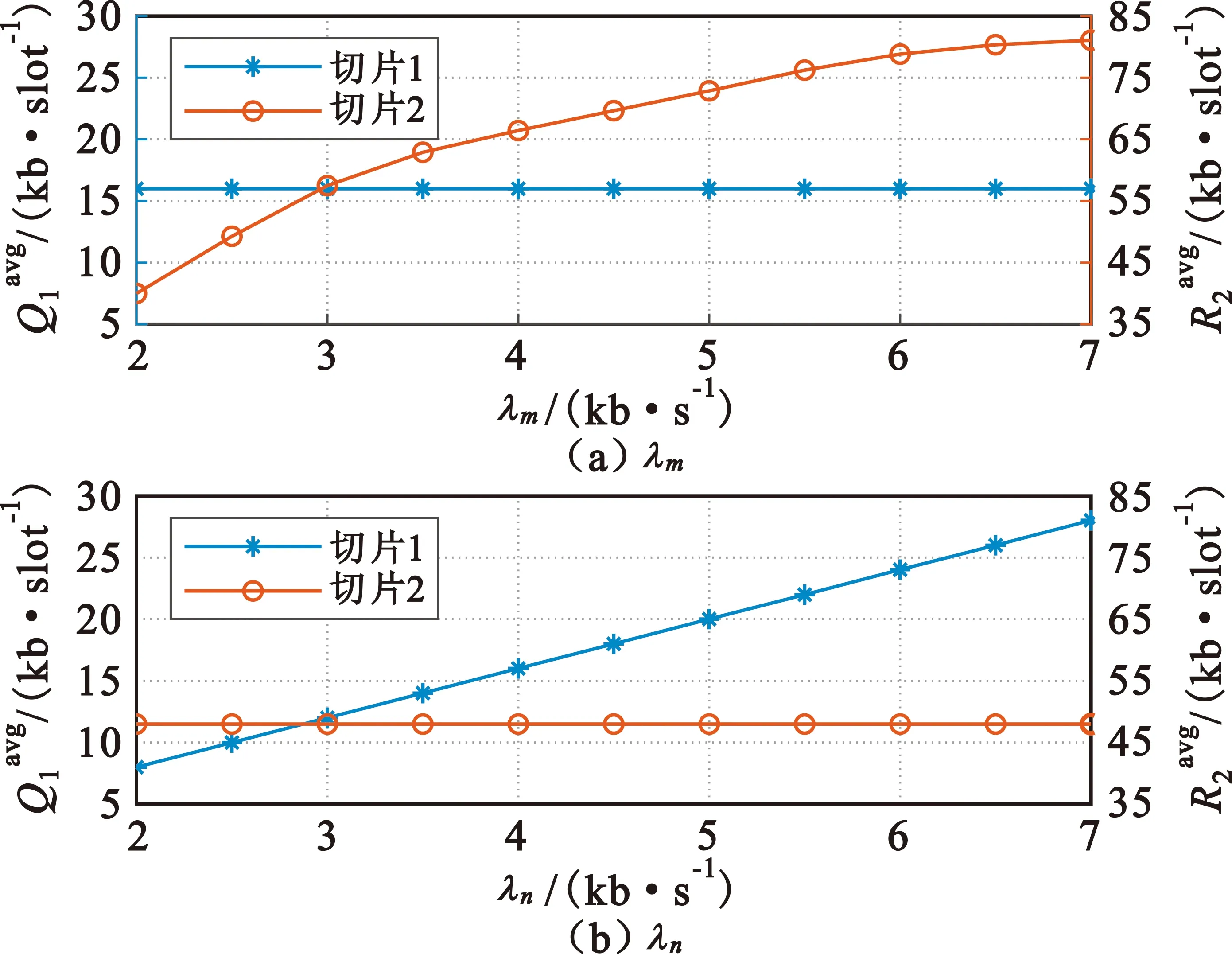
图6 切片1平均队列长度和切片2平均和吞吐量与λn和λm的关系

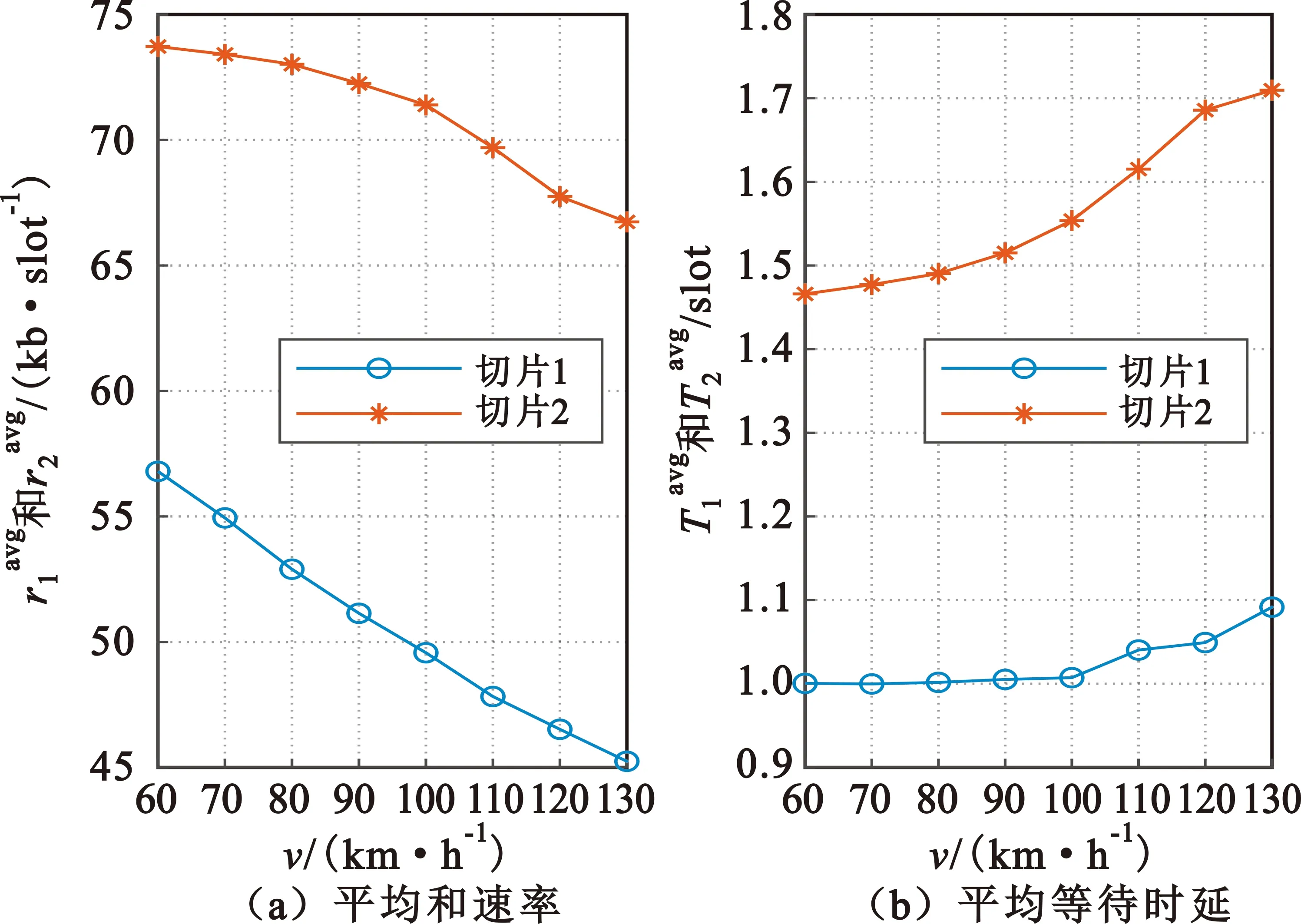
图7 平均和速率以及平均等待时延与车速的关系

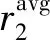
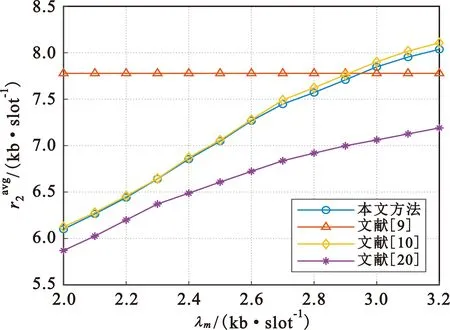
图8 不同方案的平均和速率对比

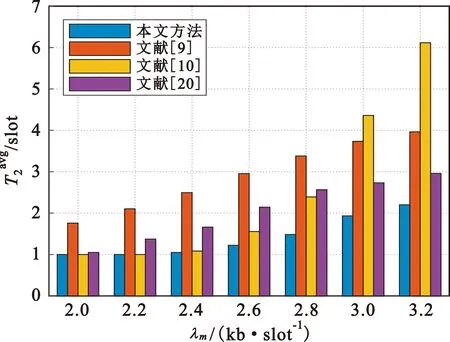
图9 不同方案的平均等待时延对比

4 结束语

本文研究了车联网中基于网络切片的联合接入数据量控制的RB分配和功率控制问题。所提资源分配方案在保证每个切片QoS的前提下，最大化信息娱乐服务切片的平均和吞吐量。通过分析可知吞吐量和时延之间存在一个权衡，可以根据实际需求选取合适的控制参数V。此外，已有方案进行的比较结果表明，本文方案具有更好的时延性能，对车联网切片部署具有一定的参考价值。在未来的工作中，将进一步考虑车辆密度的变化，以期实现更灵活的切片方案。