基于设备实时故障率的配电网停电概率计算方法

方健，林翔，王红斌，尹旷，方敏，李盛楠

(1.广东电网广州供电局， 广州 510620； 2.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044)

0 引 言

配电网设备数量众多，容易受到大风大雨、设备负载率等因素的影响，从而导致故障停电的频繁出现[1]。传统的风险评估大多使用设备的历史故障率来计算各负荷点的停电概率，然而配电设备的故障率会因运行环境而变化，造成不同支路的停电风险不同。如果能够计算出配电网的实时故障率实现状态维修,这不仅可以提高配电网的供电可靠性，还能节省财力物力。

目前，配电网的停电概率计算模型主要包括完全或部分使用配电设备的历史故障率这两种。在完全使用配电设备的历史故障率的研究中，使用分块技术[2]、可靠性跟踪[3]、贝叶斯网络[4]、主成分分析[5]计算了各负荷点的停电概率，找出了配电网的薄弱环节。由于没有考虑配电设备故障率在不同运行环境下的变化情况，结果并不能准确反映配电网实际风险情况。在部分使用配电设备的历史故障率的研究中，没有考虑设备运行环境的影响；文献[6-8]考虑大风、大雨、雷击、电气等因素以及设备运行状态，建立了基于设备停电实时故障率的风险评估模型。但是该方法中故障率基准值使用的年平均故障率，忽略了小动物、树木破坏等外力对故障率的影响，没有考虑不同故障并发时的协同效果。

为了实现配电网设备差异化的停电概率评估，有学者利用健康指数建立了数学模型来反映配电设备实时故障率。文献[9-10]指出配电设备健康指数能够反映设备的实时状态，并可以用指数模型来反映，但是文中并没有阐释指数模型中待定系数如何准确测定。文献[11-12]使用配电设备的常用故障率、最小故障率以及设定的健康指数，通过逆运算得到了指数模型中的待定系数；由于不同地区的配电设备存在差异性，所以常用故障率及最小故障率对应的健康指数不可能是相同的，因此这样确定的指数模型不能有效反映设备的实时状态。

针对以上问题，文章提出了计算配电设备实时故障率的两种方法，首先将配电设备历史故障率按照月份统计，接着利用基于故障因素参数修正的方法对历史故障率进行修正，并在一定程度上考虑了主要因素之间的协同作用，快速计算出同一地区同类型的配电设备实时故障率；接着将计算得到的故障率修正值代入基于健康指数的配电设备实时故障率指数模型，从而确定指数模型中的待定系数，逐一计算各设备的实时故障率。然后使用馈线分区方法计算各负荷点的故障停电概率和停电时间，最后通过广州地区线路验证了方法的有效性。

1 配电网主要停电因素分析

图1为广州某地区2013年～2018年主要故障停电因素统计，可以看出,在设备故障停电中，小动物、树木影响等外力破坏、雷击等自然灾害以及设备超期服役老化是该地区故障停电的主要因素。利用主要停电因素对历史故障率进行修正时，主要对规律性较强，且发生数量较多的因素进行分析计算。

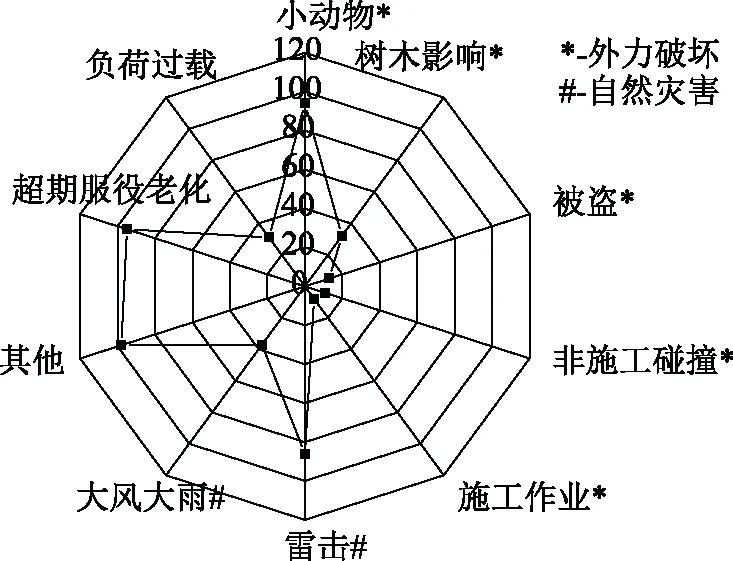
图1 主要故障停电因素统计

前人在故障率修正过程中，使用的故障率基准值是年平均故障率，在此情况下由于小动物、树木影响等外力破坏对设备故障率的影响规律难以拟合。然而在广州从化、白云等地区外力破坏因素发生频率高，因此不能忽略这些因素对故障率的影响。对于被盗、非施工碰撞、施工作业等造成的故障停电，对故障率的影响规律拟合效果差，因此在参数修正过程中归为其他类故障因素。对于其他类故障因素，只考虑这些因素所占权重，修正系数取1。

通过统计分析广州市配电网故障历史数据发现，每年的3月～5月，小动物侵害导致架空线路发生故障的情况最严重；每年的夏季初期到秋季末期，树木破坏导致中压架空线路发生故障的情况最严重。同时将设备故障率按照月份进行统计，发现12个月的故障率差异较大，但相同月份设备故障率基本相同。因此文章的故障率基准值使用连续几年每个月的设备平均故障率，同时由于小动物、树木对设备故障率的影响随季节变化，因此这里认为连续几年相同月份树木对设备故障率的影响相同。

2 基于主要故障因素的设备实时故障率改进模型

2.1 故障停电因素权重计算

配电设备主要考虑电缆、架空线、柱上断路器、柱上隔离开关、柱上负荷开关、变压器等6类设备，故障率用λi(1≤i≤6)。根据图1的统计结果，这里考虑设备超期服役老化、负荷过载、雷击、大风、大雨、小动物、树木影响以及其他等七类因素，在故障中所占权重用ωj(1≤j≤7)。这里用ωij表示在第i类设备中第j种故障因素所占权重。

统计第j种故障因素导致第i类设备发生故障的数量Nij，如式(1)所示：

(1)

将同类设备中各种故障因素进行归一化，得到第j种故障因素对第i类配电设备的权重ωij,如式(2)所示:

(2)

2.2 故障停电因素修正系数计算

原有研究忽略了小动物等外力破坏对故障率的影响，同时没有考虑不同故障并发时的协同效果。通过统计分析可以得到不同因素的修正系数cij，表示第j种故障因素对第i类配电设备的修正系数。

2.2.1 设备超期服役老化修正模型

如图2所示，配电设备的故障率变化符合浴盆曲线，可以看出故障率主要与设备运行年限有关，故障率的变化大致可以分成三个阶段。设备超期服役老化位于故障曲线的第三部分，如果未能及时根据设备的健康状况实行状态维修，则故障率会陡然升高如图2中(C)所示。

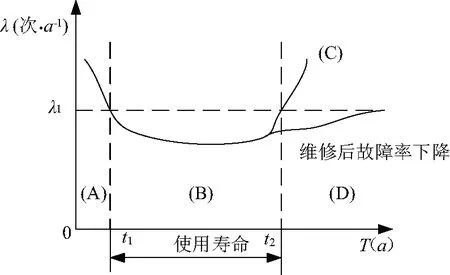
图2 配电设备的故障率曲线

各设备超期服役老化修正可以利用Weibull分布来拟合，如式(3)所示[6]:

(3)

式中T为运行时间，t1为区域B偶发故障期开始时间，t2为区域C耗损故障期开始时间。未知参量β可以用极大似然估计法求解，将配电设备运行年限与设备故障率的历史数据带入构造的似然方程组中，对方程组进行优化求出β。

2.2.2 负荷过载修正模型

广州地区夏季的下午和傍晚这两个时间段是用电高峰期，设备由于负荷电流较大容易发热导致故障停电。因此负载率与设备故障停电有着正相关的关系，负荷过载值LOV可以用式(4)表示：

(4)

式中L为配电设备的实时负载率,L1为额定负载率。由于设备过载引起的设备实时故障率的变化，在计算出LOV的前提下可以用指数型效用函数表示，因此负荷的过载修正模型如式(5)所示：

(5)

式中Llim为配电设备的最大负载率。

2.2.3 雷击、大风大雨修正模型

由于只能统计配电设备每个月的历史故障率，因此需要使用待评估设备所处天气情况与历史天气情况进行比较，从而找出修正系数。根据广州地区的气象局连续n年的雷电和降水量数据，则雷击、大风大雨气象因素修正值如式(6)所示：

(6)

式中M为待评估月天数；Nm为待评估月第m天雷击次数或降水量；Ni为统计年第i个月雷击次数或降水量。

2.2.4 小动物破坏修正模型

老鼠等小动物造成从化、南沙等地区架空线和避雷器发生故障的案例较多，广州地区部分配电设备上装有小动物监测和驱赶装置，统计连续n年小动物出现次数，拟合得到小动物破坏对于故障率的影响修正值如(7)所示：

(7)

式中Sm为待评估月监测到的设备上小动物出现次数；Si为统计年第i月的小动物出现次数。

通过统计发现，连续几年相同月份树木对设备故障率的影响基本相同，因此树木影响对故障率的修正系数取ci6=1，同时其他次要因素由于难以统计数据或规律性，拟合效果差，因此文中取ci7=1。

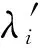
(8)

在单一故障发生，多故障并发但相互之间没有明显协同作用时，式(8)能够有效计算同类型配电设备的实时故障率。对于多故障并发且协同作用明显时，比如配电设备同时出现运行时间T>t2及实时负载率L>L1，即超期服役的设备在负荷过载时，发生故障的概率大于式(8)计算出来的结果，此时需要分别在两者的修正系数cij上乘一个协同系数c′。

对广州地区280个超期服役且在负荷过载时发生故障的设备进行统计，结果如图3所示。参考式(3)、式(4)，图中X轴表示差值L-L1，Y轴表示T-t2，Z轴表示协同系数c′。可以看出实时负载率超过额定负载率主要集中在10%～20%范围内，故障发生的年限超过耗损故障期主要集中在2年～8年，c′主要集中在1.2～1.4。通过拟合得到，协同系数c′与超役年限x、超额负载率y的表达式如式(9)所示:

Z=1.657-8.693x-0.03453y+42.63x2+

0.9156xy+0.001483y2-77.58x3-1.003x2y-

0.03983xy2

(9)

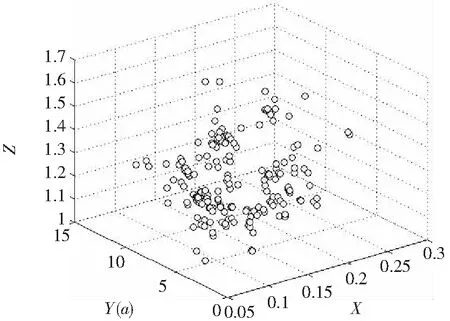
图3 超役年限、超额负载率与协同系数的关系

同样，对于超期服役老化和大风大雨这些具有明显协同作用的故障因素，也可以参照这种方法进行计算c′。根据广州地区的统计结果，发现c′取值一般范围为1.1～1.6，实际大小与具体使用年限、实时降雨量、风力级别、雷电次数等有关。

3 基于健康指数的配电设备实时故障率模型

健康指数H的大小由状态参量的实时劣化程度和权重决定。建立并量化健康指标，接着利用SPSS软件对配电设备分层、分部件进行多参量统计，确定指标权重及健康指数评价模型[13]。关键部件及特征参量的选择可参考南方电网公司2010年颁布的标准S.00.00.05/Q100-0006-0912-814《广东电网公司设备状态评价与风险评估技术导则》。

相关研究表明，配电设备的健康指数与设备实时故障率λ′之间呈指数关系，如式(10)所示:

λ′i=AeBH

(10)

式中A、B为待定系数。文献将常用故障率、最小故障率以及相应的健康指数代入式(10)，从而求解出待定系数。由于不同地区不同设备之间存在差异性，该方法计算出的待定系数使得模型误差变大。由于使用不同方法计算设备在同一时刻的的故障率应该相等，当设备在建立了修正模型的这些因素下发生故障时，式(8)的计算结果更加符合实情。因此将式(8)在计算准确情况下的λ′和H实时带入式(10)，待定系数可以利用最小二乘法拟合得到。为了与原有方法计算得到的健康指数模型区分，由此得到的健康指数模型称为改进的健康指数模型。

将广州某地区的实时故障率λ′与对应的健康指数H代入，得到电缆、架空线、柱上断路器、隔离开关、负荷开关、变压器的数学模型如下所示:

λ′Cab=0.7233e-0.0444H

(11)

λ′Ove=1.7720e-0.0577H

(12)

λ′Bre=0.0971e-0.0302H

(13)

λ′Iso=1.7213e-0.0572H

(14)

λ′Lod=1.8543e-0.0466H

(15)

λ′Tra=9.4065e-0.0681H

(16)

4 基于实时故障率的配电网可靠性指标计算

传统的可靠性评估根据网架结构，然后利用设备的年平均故障率和故障修复时间来计算负荷点的停电概率和停电时间，而这不能反映配电网的真实风险水平。因此文章采用“馈线分区”计算各负荷点的停电概率和停电时间[14]。其主要步骤如下：

(1)以断路器、熔断器、负荷开关等开关元件为界将复杂的网络结构划分为多个分块，然后根据元件间的串联关系计算每个分块的故障率λ′k和修复时间t′k，如式(17)、式(18)所示：

(17)

(18)

式中m为分块内元件个数；n为分块数量；λ′i为元件实时故障率；ti为元件平均修复时间。

(2)在步骤(1)中，配电设备实时故障率计算有第2节、第3节介绍的基于改进的故障因素修正、基于改进的健康指数这两种方法。倘若只需了解各条线路上不同负荷点的停电风险时，使用基于改进的故障因素修正的设备实时故障率模型，该方法能够快速评估同一条线路上相同类型设备的实时故障率；随着泛在电力物联网的建设，配电设备的在线监测数据逐渐完善，当需要评估某个特定设备的实时故障率、负荷点的停电风险或者前面的方法不能准确计算故障率时，使用基于改进的健康指数的实时故障率模型。

(3)不同分块之间也属于串联关系，根据网架结构计算各负荷点的故障实时停电概率和停电时间。

5 实例分析

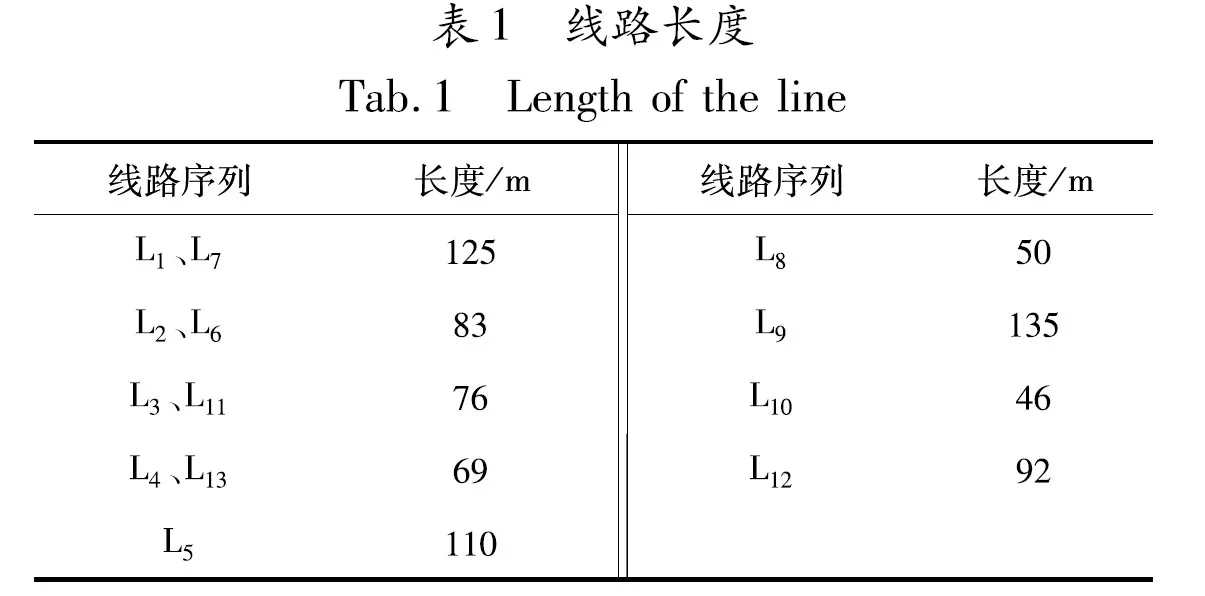
这里以广州市某条线路在2018年6月8日发生故障停电概率为例，图4为该条线路的网架结构图。图中母线BUS1是上级电源的注入点。线路由1个隔离开关(IS)、2台断路器(B)、8台变压器(T)、8个负荷点(LP)以及一共16个负荷开关组成。16个负荷开关包括8个一般负荷开关、6个熔断器式负荷开关，2个具有自动释放功能的负荷开关，16个负荷开关的故障率统一使用柱上负荷开关(LS)的故障率。设备负载率额定值L1为0.7，最大限值Llim为1.1。线路长度如表1所示。

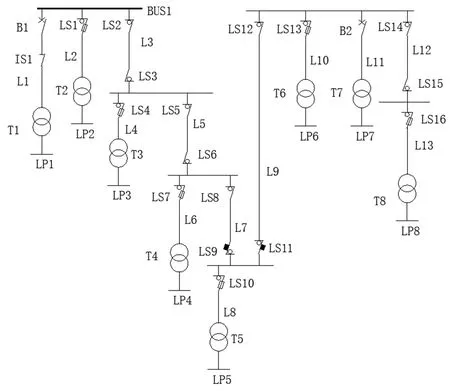
图4 配电网算例系统

统计该地区2013年～2018年配电网故障发生的次数，代入式(2)得到权重情况如表2所示。表格中I1～6分别表示电力电缆、架空线、断路器、隔离开关、负荷开关、变压器共6类配电设备，J1～7分别表示设备超期服役老化、负荷过载、雷击、大风大雨、小动物、树木破坏以及其他共七类主要故障影响因素。

该地区6类设备在6月份的月故障率及故障修复时间情况如表3所示。将各设备的历史数据代入Weibull模型拟合，可以得到式(3)中的β值，结果如表4所示。各类设备的偶发故障期开始时间t1，耗损故障期开始时间t2以及投运时间T如表4所示。

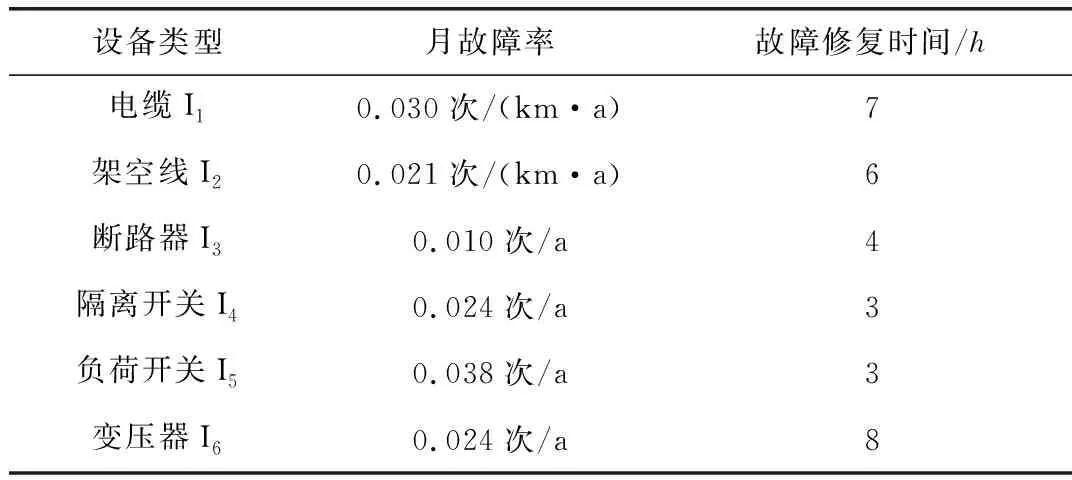
表3 配电设备的故障参数

将表4的数据代入式(3)可以得到I1～6设备超期服役老化修正参数如表5所示。

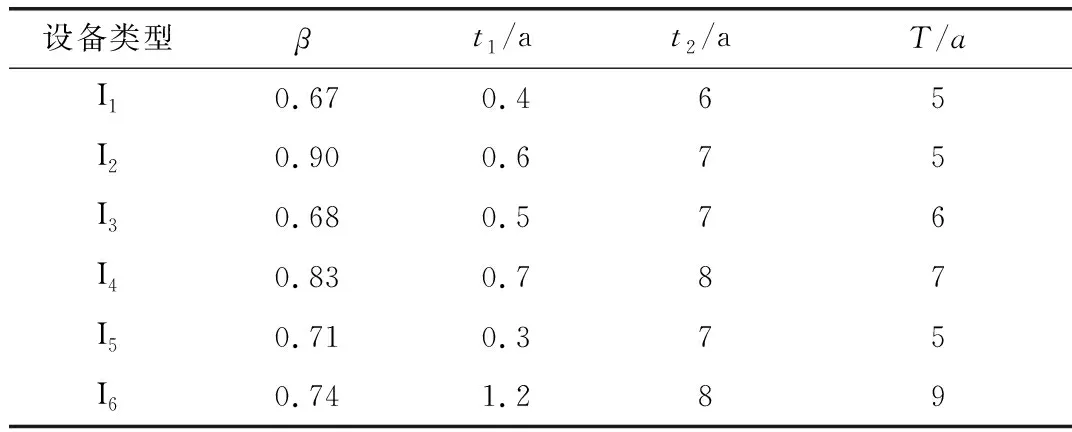
表4 配电设备的运行情况

表5 设备超期服役老化修正参数

由于负载率额定值L1为0.7，而该条线路的6月份该天的最高负载率为15.68%，因此LOV=0,I1～6的负荷过载修正系数ci2=0。

通过雷电定位系统发现当天该地区发生雷击2次，该地区连续3年5月份总共发生10次雷击，带入式(6)得到当天的雷击气象因素修正值ci3=18.6。天气预报历史数据查得该地区2018年6月8日的降雨量30.1 mm，该地区2013年～2018年的6月降水量一共为1 428.6 mm，带入式(6)得到大风大雨修正系数ci4=3.79。通过监测设备发现该地区当天没有出现小动物，因此ci5=0。

由于变压器出现了超期服役，且当天下雨，根据广州地区的统计结果，变压器的ci1和ci4分别乘以协同系数c′=1.2，得到c′i1=2.12，c′i4=4.55。

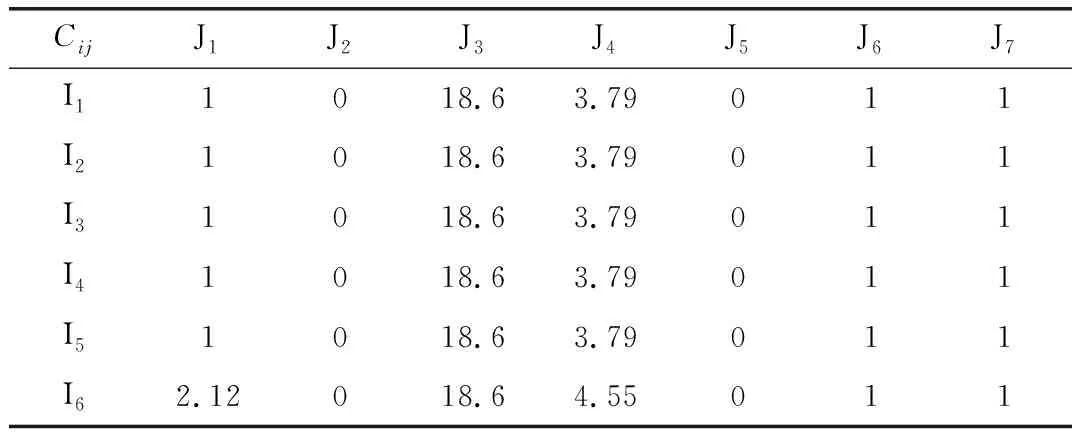
表6 不同故障因素修正系数

根据实际统计结果，这里不考虑其他因素的协同作用。2018年6月8日的设备状态修正系数矩阵如下，每一行代表不同故障因素在同类型设备中对应的修正系数。

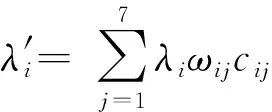
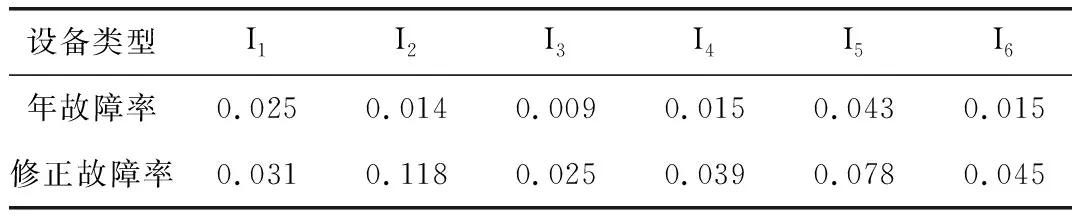
表7 基于修正值的设备实时故障率

根据在线监测等数据可以计算出各设备的健康指数以及实时故障率，如表8所示。可以看出基于健康指数的实时故障率改进模型的差异化性能最好，能够反映每个设备的实时故障率；而基于改进的故障因素修正模型次之，一般用于计算同类型同型号的设备实时故障率；基于历史年平均故障率的差异化性能最差。

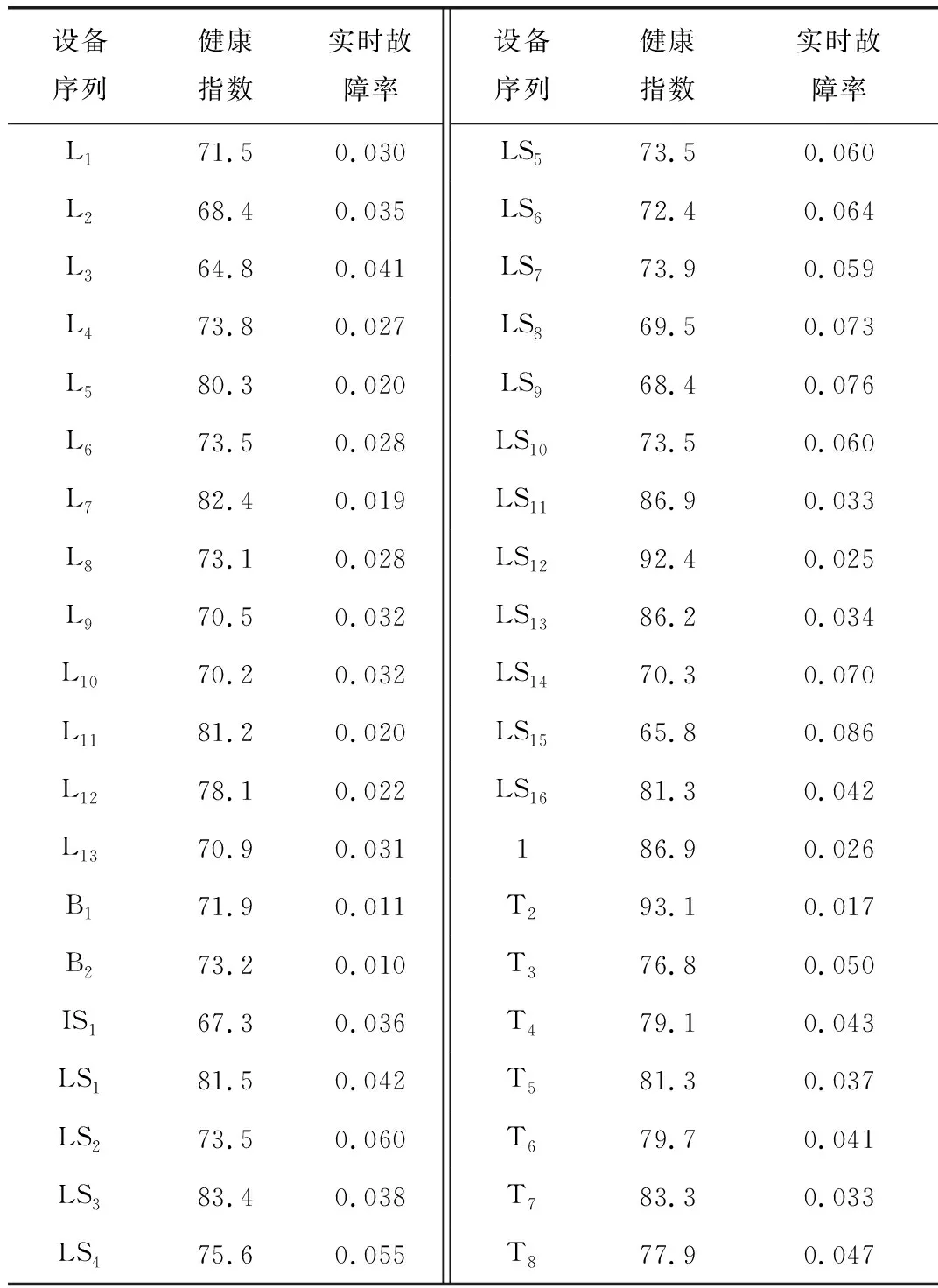
表8 健康指数及实时故障率

在该算例中，分别使用各配电设备的年历史故障率、基于改进的因素修正故障率、基于改进的健康指数模型的实时故障率，结合“馈线分区”的方法，计算出各负荷点的故障停电概率和停电时间如表9、表10所示。可以看出，当出现雷雨天气时，基于改进的参数修正和健康指数的两种实时故障率模型计算出来的各负荷点的故障停电概率，都高于基于历史年平均故障率计算出来的结果；但是三种方法计算出来的各负荷点的故障停电时间相差无几。

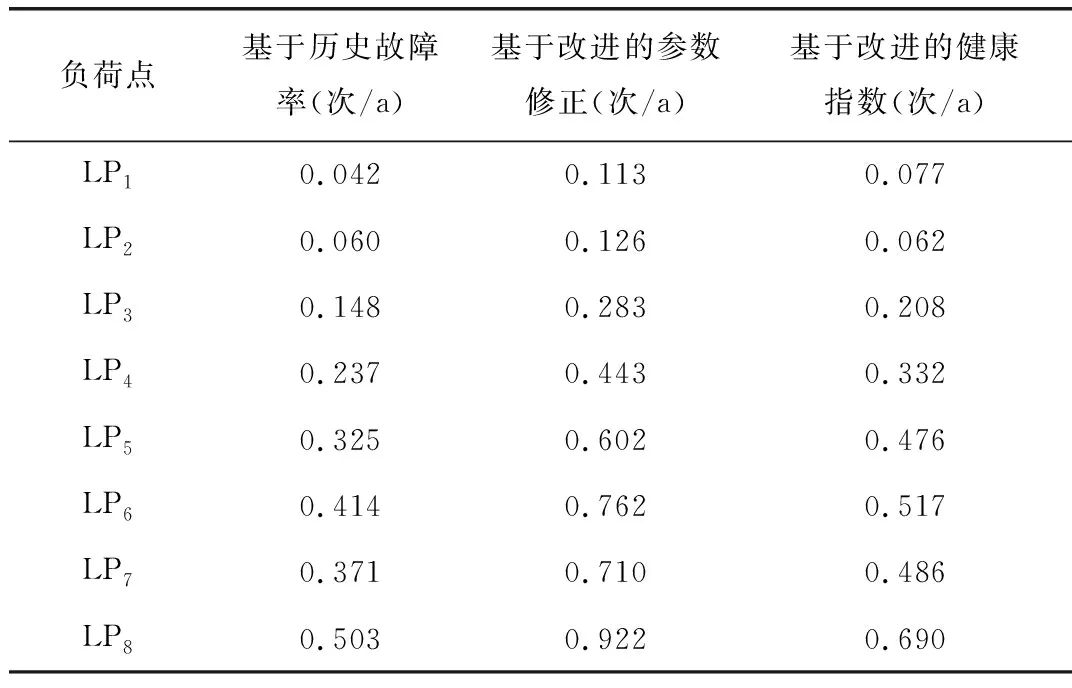
表9 三种方法计算出来的负荷点故障停电概率

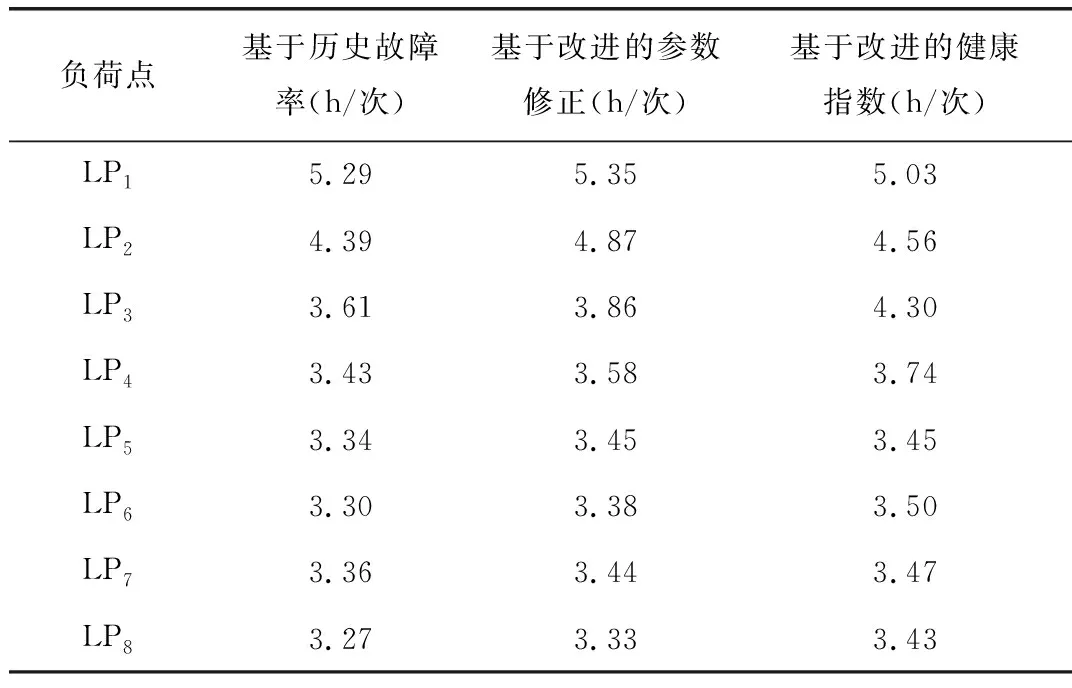
表10 三种方法计算出来的负荷点故障停电时间

为了验证所述方法的有效性和适用性，利用历史故障率、传统的主要故障因素修正[7]、基于健康指数、以及所提出的基于改进的主要故障因素修正、基于改进的健康指数模型，共五种方法对广州地区不同线路的280个发生故障的负荷点进行了计算。结合所述方法实施的实际效果，当计算结果与事后统计的实际故障率的误差范围在10%左右时，此时的运行维护效果既能较大程度减少故障停电次数，同时人力物力资源的使用也较为合理。因此这里认为计算结果在各负荷点实际停电概率±10%范围内时，则计算结果准确，结果如表11所示。

表11 三种方法计算结果的准确率

可以看出利用历史故障率来评估负荷点的停电概率效果最差，主要是因为历史故障率不能有效反应设备的实时风险情况。传统的基于主要故障因素修正的方法，由于考虑了主要故障因素的影响，准确率比前者提高了10%左右。基于改进的主要故障因素修正的方法，由于使用月平均故障率作为基准值，在一定程度上考虑了小动物、树木等外力破坏的影响，以及不同故障因素之间的协同效应，因此准确率有了较大提升。准确率仍不高可能是因为该方法只对大部分规律性较强的故障因素进行了修正，而当没有考虑的故障因素导致的故障停电发生较多时，则准确率会发生下降。这个结果与传统的使用最小故障率和常用故障率的健康指数模型计算结果接近。而基于改进的健康指数模型在五种方法里面准确率最高，但仍没有达到90%。可能是因为基于健康指数的故障率模型中待定系数的计算，依赖于基于改进的主要故障因素修正方法的计算结果。但是由于该方法主要受设备实时健康指数的影响，因此计算结果准确率最高。

6 结束语

(1)文章对传统的主要故障因素修正模型进行了改进，在使用月平均故障率的基础上，对原有方法忽略的小动物、树木影响因素进行了修正，并在一定程度上考虑了主要因素之间的协同作用，可以有效计算同一地区同型设备的实时故障率;

(2)文章利用基于健康指数的故障率模型与故障因素参数修正模型之间的联系，确定了基于健康指数模型中的待定系数，得到了改进的健康指数模型。当需要了解单个配电设备的实时运行状态时，根据在线监测量等信息可以计算健康指数，进而逐一计算配电设备的实时故障率;

(3)实例分析验证了论文所提两种方法的有效性，结果表明在雷雨天气，基于实时故障率的两种方法计算出来的各负荷点的故障停电概率均高于使用历史值的方法，更加符合实际情况，有利于实现配电网的风险评估、风险预警及状态检修。