虚拟电厂参与下含高渗透可再生能源系统的运行策略

余英，王海云，王维庆，武家辉，李笑竹

(新疆大学 可再生能源发电与并网技术教育部工程研究中心， 乌鲁木齐 830047)

0 引 言

现代电力系统大规模可再生能源并网，其出力波动性导致系统需要提升灵活响应不确定性的能力，同时各竞争主体的不断增加对传统电力市场带来巨大冲击。未来的电力市场将是开放化和多元化的[1]，在多种市场主体参与下需求响应能够提高用户参与调度的积极性，实现电力需求供给与消费协同，是平衡新电改下各市场主体利益诉求的绝佳手段。虚拟电厂(Virtual Power Plant，VPP)技术的兴起使大规模灵活控制分布式可再生能源和可控负荷，参与系统市场交易和优化调度成为可能，并有效解决系统对大量不同类型负荷调控难的问题。同时VPP以一种新的运营模式作为独立市场主体参与电力系统调度，其利润与电力系统收益之间形成的复杂博弈关系将进一步加深不确定性对分销系统[2]安全经济运行的影响。由此研究虚拟电厂参与下的电力系统各收益主体之间的效益制约关系，对灵活运行调度，平衡电力供需，保证电力经济的可持续性发展有着重要的现实意义。

现阶段研究中，国内外学者的研究主要集中在对虚拟电厂的运行模式及经济策略上[3-8]，提出核-火-虚拟电厂三阶段联合调峰模型[3]，虚拟电厂参与下热电联合优化调度[4]，配电网与VPP双层优化模型[5]，考虑需求响应交易市场的虚拟电厂多阶段竞价策略[6]，配电网与VPP双层优化模型[7]，探索了虚拟电厂对电力系统多时间尺度的响应能力[8]。但上述模型均未考虑大规模可再生能源并网后对系统带来的不确定性，并不适用于现代电力系统，也没有探索不同资源配置下的虚拟电厂对电力系统运行策略带来的影响。同时优化调度的关键问题是如何求解模型，许多学者采用二阶锥凸优化处理非线性因子，列约束生成算法，大M线性化[9]，分枝定界法[10]，但这些方法虽然效率高、速度快，但过程复杂，通常不能直接求解。此外对目标函数要求严格，不可微和非凸形式无法求解，且初始值难以选取，容易陷入局部最优，不能保证其解的可行性和最优性。随着人工智能技术的兴起，智能算法被有效应用在电力系统的优化调度问题上[11-14]，但该问题通常涉及众多决策变量且类型不一，包含大量复杂的等式与不等式约束。因此针对模型特点提出相应求解方法也是研究热点之一。

为规模化的灵活控制分布式可再生能源与可控负荷参与系统市场交易和优化调度，提出一种VPP参与下含高渗透可再生能源的双层优化调度模型。上层模型优化系统运营收益，制定系统内机组运行策略，下达对VPP的调度计划；下层模型由VPP响应调度计划并进行其内部资源的协调分配，两层之间交替求解实现协同调度；同时利用威尔分布、贝塔分布模拟风电、光伏的随机性，计及可再生能源出力不确定性带来的高估与低估成本。并且利用一种新颖的MOMFO算法对模型进行求解，通过修改后的IEEE 39节点模型验证模型可行性与算法竞争性，并分析虚拟电厂的参与对系统总成本的影响，及不同渗透率下的可再生能源系统对虚拟电厂调度计划的影响，也进一步验证了所提出的模型可均衡各层收益主体，在维持安全稳定运行的前提下，系统运营利润最大化，有效实现了电力系统的可持续性发展。

1 不确定性分析

风电、光伏的输出功率分别受风速、太阳能辐射度的影响具有随机性。下面分别用威布尔分布[15]、贝塔分布[16]的概率密度函数描述风速、辐射度，再分别通过风速、辐射度与输出功率的关系，得到风电、光伏输出功率的概率密度函数。

1.1 风电输出功率的每小时特性

威布尔分布被认为是描述风速分布的最合适的模型，其概率密度函数(PDF)可以用来描述风电场中风速的概率分布。式(1)中WSt为t时段的风速，kt、ct分别为威布尔分布在t时段的形状参数与尺度参数。

(1)

假设风电机组的输出功率与风速之间的关系为一个简单的分段线性函数，则输出功率可由风速表示，见式(2)。式中WSin、WSoff、WSR分别为选用风机的接通、切断与额定风速；PWR为风电机组的额定输出功率，选用Enercon E82-E4涡轮机，WSin=3 m/s，WSoff=25 m/s，WSR=16 m/s。

(2)

由于随机变量风速的函数风电机组输出功率是一个不连续的分段函数，因此机组输出功率的概率密度函数也是不连续的，分别在PWt=0与PWt=PWR两处，见式(3)。

fPW,t(PWt)=

(3)

1.2 光伏输出功率的每小时特性

贝塔分布可以用来描述太阳能辐射度的分布，其概率密度函数见式(4)，其中SIt为t时段的太阳能辐射度，at、bt分别为贝塔分布在t时段的形状参数。

(4)

光伏机组输出功率与太阳能辐射度之间的能量转换关系见式(5)，式中SImax为最大太阳能辐射度，设置为1000 W/m2；SIC为定点辐射度为120 W/m2；PSR为光伏机组的额定输出功率。

(5)

由于随机变量太阳能辐射度的函数光伏机组输出功率式(5)是一个分段函数，因此光伏机组输出功率的概率密度函数也是不连续函数，见：

fSIt(PSIt)=

(6)

1.3 概率密度函数参数选取

选取某地区(气候终年温和阳光充足，全年日平均气温维持在25 ℃左右)全年度的太阳能辐射度与风速数据共8 760个样本，拟合威布尔的控制参数kt、ct与贝塔分布的控制参数at、bt取值见图1。

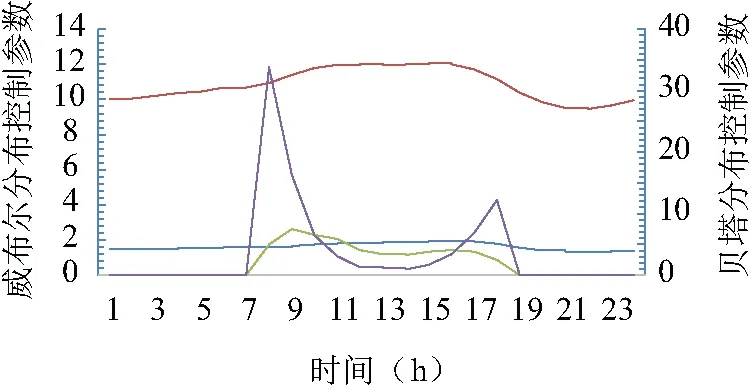
图1 各时段威布尔分布与贝塔分布的参数

2 双层优化调度模型

2.1 系统能量管理策略

采用双层多目标优化对其进行建模，其中电力系统调度位于模型上层，VPP位于下层。调度系统与VPP相互耦合，VPP的运行决策受调度系统计划影响，反之系统调度策略会根据VPP对调度计划的响应反馈而调整，使得调度计划在两层之间偏差最小。为提升系统在高渗透可再生能源下灵活响应不确定性的能力，调度系统通过对VPP及常规发电机组的调度满足系统内负荷需求并保证能量交换得到平衡[17]。VPP整合管辖区域内分布式可再生能源、可控负荷及储能装置响应配电网下达的调度指令，将任务分解至各个可调度单元上，其运营过程及结构见图2。

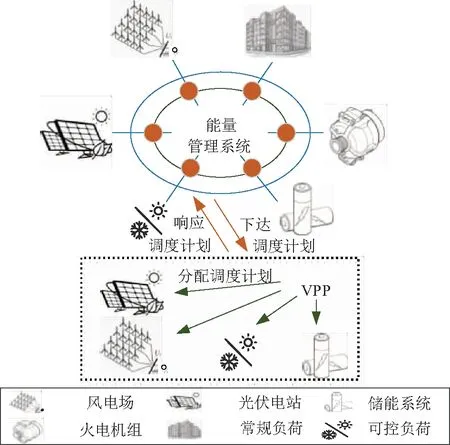
图2 系统运营结构图

优化时先由调度系统向VPP发送调度计划，VPP在满足自身运行约束的前提下对该调度计划实行初步响应，并将自身优化的结果反馈至上层，调度系统根据反馈结果进一步调整计划，使得两层调度计划偏差最小。过程中上下两层信息互相更新与传递，实现系统与VPP之间的互联互通，在尽可能地满足各系统电力需求的前提下，经济性最好。虚拟电厂包含储能系统(ESS)、分布式可再生能源，其中储能系统接受调控，分布式可再生能源不接受调控且不计发电成本。交直流负荷参与虚拟电厂调度，根据其用电特点分为四类：

(1)常规负荷(Conventional Load，CL)：具有较大随机性与波动性且不接受调控，如个人日常用电负荷；

(2)可转移负荷(Transferable Load，TL)：一般具有储能能力，在不影响使用舒适度的前提下可将其转移，转移补偿价格系数较低，如空调、热水器等；

(3)迎峰负荷(Peak Catering Load，LSⅠ)：为保证自身工作运行，切负荷量较低，一般为该类型负荷总量的15%，且补偿价格指数较高，如商业负荷；

(4)避峰负荷(Peak Avoiding Load，LSⅡ)：用电灵活性较大，切负荷量较高一般为该类型负荷总量的30%，且补偿价格指数较低，如生产企业等工业负荷。

2.2 上层模型

目标函数1：总调度周期内调度成本最低。

系统运营成本由虚拟电厂、常规机组、风电/光伏运行成本组成，见:

minf1.1=CVPP+CG+CW+CSI

(7)

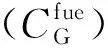
(8)

(9)

风电运行成本包括调度系统购买风电的直接成本，与风电实际输出功率低于计划输出功率的惩罚成本与高于计划输出功率的储备成本，见：

(10)

式中NW为风电机组的数量；FWj为第j台风电机组的直接成本系数；kpWj与krWj分别为第j台风电机组的惩罚成本系数与储备成本系数；PWj,t与PWj,tur,t分别为第j台风电机组在t时段的计划输出功率和实际输出功率。与风电运行成本类似，光伏发电运行成本见：

(11)

式中NS为光伏电站的数量；FSIk为第k台光伏机组的直接成本系数；kpSIk与krSIk分别为第k台光伏机组的惩罚成本系数与储备成本系数；PSIk,t、PSIk,tur,t分别为第k台光伏机组在t时段的计划输出功率和实际输出功率。

目标函数2：系统与VPP层调度偏差最小。

(12)

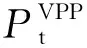
在上述配网层目标优化中还需满足如下约束条件：

(1)常规机组运行约束。

(13)

(14)

(15)

(16)

(2)VPP调度约束。

(17)

式中PVPP-u为VPP调度界限。

(3)功率平衡约束。

(18)

(4)旋转备用约束。

(1+L%), ∀t

(19)

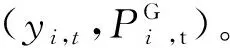
2.3 下层模型

目标函数1: VPP层的调度计划与系统的调度计划偏差最小。

(20)

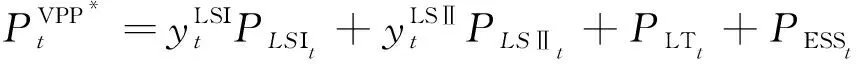
(21)

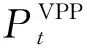
目标函数2：VPP的经济效益最好

ξLT|PLTt|+ξESS|PESSt|)

(22)

式中ξLSⅠ、ξLSⅡ、ξLT、ξESS分别为LSⅠ/LSⅡ/LT/ESS的调用补偿价格指数，yLSⅠt,yLSⅡt分别为调用LSⅠ/LSⅡ型负荷的状态变量。

目标函数3：VPP的社会效益最高，社会效益以用户用电舒适度来表征，既负荷切出、转移率最低，用电最为舒适。

(23)

式中λLSⅠ、λLSⅡ、λLT分别为LSⅠ/LSⅡ/LT占总负荷指数。

在上述VPP层的多目标优化中还需满足如下约束条件:

(1)储能约束。

式(24)为储能系统的电荷状态约束，式(25)为储能系统充放电功率约束，为保证储能系统能够可持续性的循环使用，应保证在总调度周期内其充电量等于放电量，见式(26)，储能系统充放电与电荷状态的关系见式(27)～式(28)。

SOCminER≤Et≤SOCmaxER

(24)

(25)

(26)

Et=(1-ρ)E(t-1)-ΔEt

(27)

(28)

(2)LSⅠ与LSⅡ调用约束。

LSⅠ与LSⅡ调用约束相似，以LSⅠ为例进行说明。

(29)

(30)

(31)

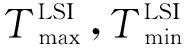
(3)LT的调用约束。

式(32)～式(33)为总调度周期内功率平衡约束、上下限约束和总负荷传递约束。

(32)

(33)

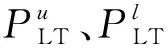
2.4 不确定变量的处理

(34)

(35)

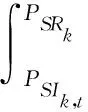
(36)

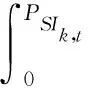
(37)

3 优化模型的求解方法

3.1 问题描述

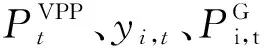
(38)

各子层优化模型涉及多个优化问题，要求在等式与不等式约束条件下同时达到各个目标函数的最小值或最大值。在此类问题中各目标函数相互制约，希望得到的是相对每个目标函数都是非劣的一组解决方案(既Pareto最优解)。为求解上述混合整数非凸非线性多目标优化问题，提出一种新型的多目标飞蛾扑火算法。

3.2 多目标飞蛾扑火算法

标准飞蛾扑火算法由Mirhalili学者在2015年提出，源于飞蛾在夜间飞行时横向定位的导航方式[18]。利用对数螺旋算子更新飞蛾在搜索空间中的位置，有效平衡算法的全局搜索能力与局部开发能力见：

(39)

式中 上标N表示当前迭代次数；M为飞蛾位置；F为火焰位置，火焰是目前飞蛾获得的最佳位置；b为表示对数螺旋形状常数，t表示飞蛾下一代位置离其对应火焰的距离，设置为[r,1]之间的随机数，r是收敛常数并随迭代次数N在[-2,-1]上线性减小(t=-2是最近距离，t=1是最远距离)。

待飞蛾位置更新后，将其适应度值与火焰的进行比较，按照优劣程度降序排列选出前flame.no个作为新一代火焰继续迭代，其中flame.no计算方法见式(40)，Nmax为最大迭代次数，flame.max为预先设定的最大火焰数量。

(40)

引入Lévy飞行避免算法出现“早熟”，式(41)为Lévy飞行策略，⊕为点对点乘法；∂是步长控制因子；best为最优飞蛾位置；L(λ)为Lévy分布；λ是[1，3]之间常量。

(41)

MOMFO基于外部精英保留和Pareto占优概念，另外，MOMFO得到的是一组pareto最优解，从问题的实际出发需要得到一个在一定程度上满足模型中各个目标函数的解。使用基于模糊数学的方式提取最优折中解，选择线性函数作为隶属度函数。求解流程见图3。

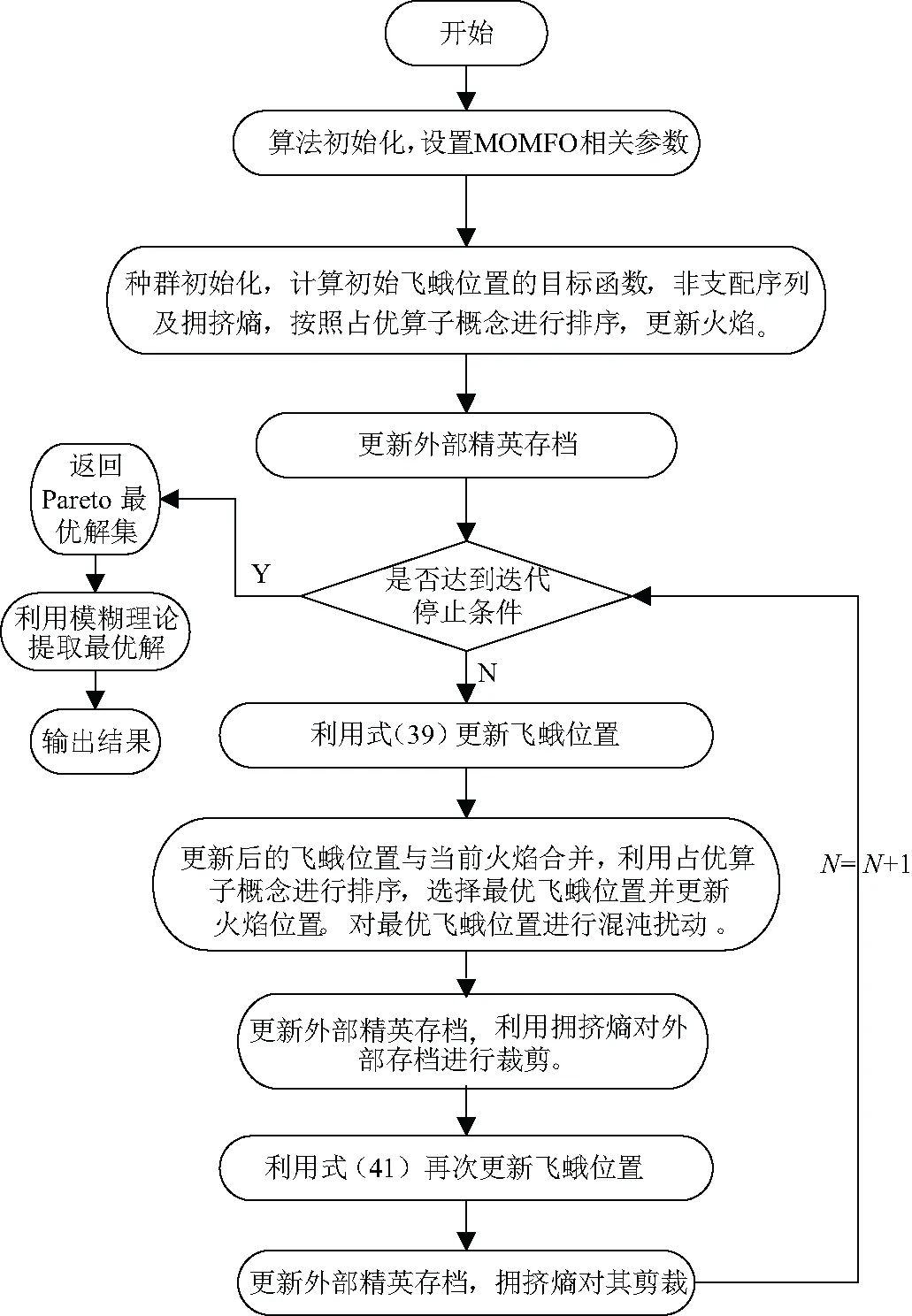
图3 算法流程图

为了测试MOMFO的有效性，选取8个经典多目标测试函数(ZDT1-3，ZDT6，SCH，DTLZ2-4)同NSGA-Ⅱ和MOEA/D两个经典多目标算法在求解上进行比较，并选取散布性(spread,Δ)作为指标进行衡量验证，Δ值越小说明非劣解具有较好的分布性，结果见表1。表1表明MOMFO获得了除ZDT2外其他所有测试函数最小的散度Δ值，更进一步说明MOMFO在保持非占优解集多样性方面优于其他两种算法。部分Pareto最优解集识别对比图(图4)也可说明MOMFO在保持非占优解在Pareto前沿的分布多样性方面要明显优于NSGA-Ⅱ。

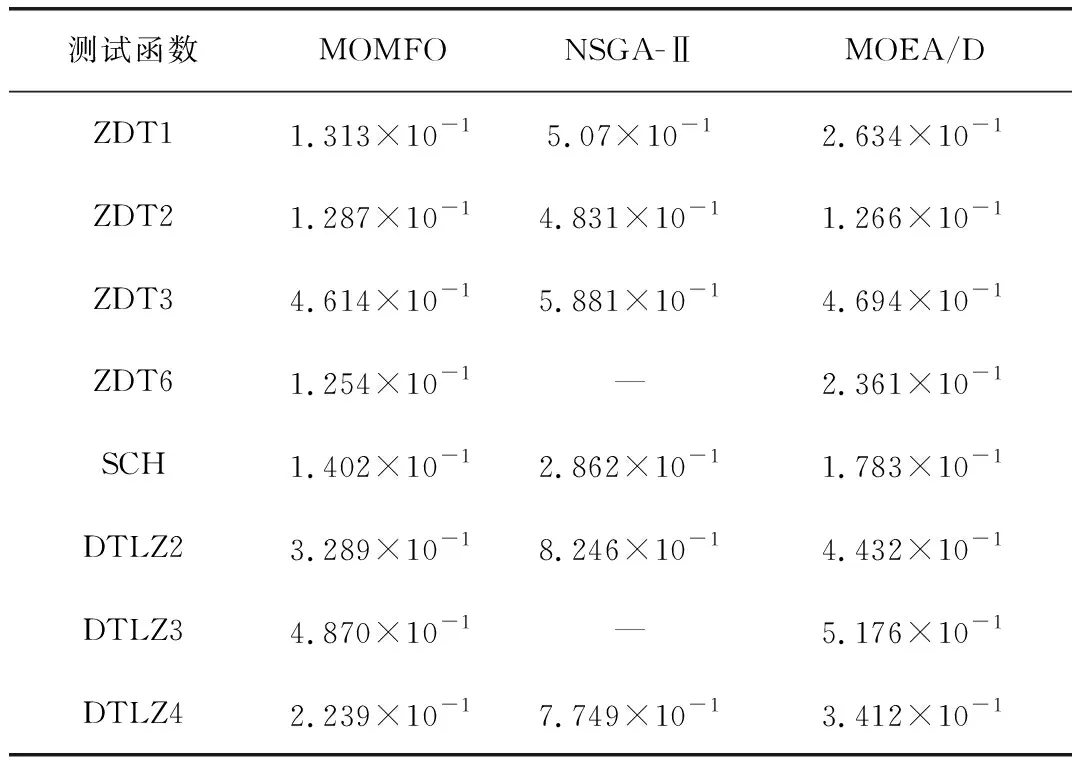
表1 Δ性能比较结果

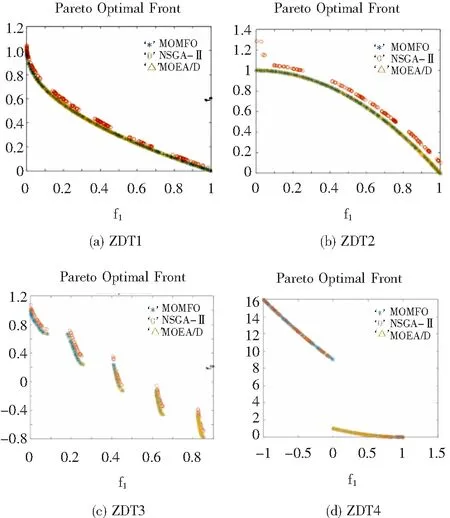
图4 部分测试函数的Pareto前沿

4 算例分析

4.1 Case1:传统IEEE 39节点动态经济调度问题

为说明提出算法的竞争力，本小节选取IEEE 39节点系统为模型，该模型是由10个火电机组组成的传统动态经济环境调度模型[19]，模型中考虑火电机组阀点效应、功率平衡约束、爬坡约束，计及网络损耗，并利用Kron损失系数法计算线损。系统各火电机组耗量特征系数、排放特征系数及火电机组输出功率界限值、系统负荷等相关运行参数与文献[20]一致。多目标算法设置如下：种群规模Np=150，最大迭代次数G=2 000次，最大外部精英存档Amax=150，最大火焰数flame.max=150，混沌变尺度收缩因子β=1。

图5为非占优解集在模糊决策后得到最优折中解，即各发电机在各个调度时段的输出功率，包括网损与负荷，均可在图5每个区间校验。为了说明提出算法在求解DEED问题上的竞争力，将最优折中解所对应的燃料成本与污染排放与其他算法在相同模型下所得折中解的结果进行对比，见表2。

从表2可以明显看出，与其他文献的算法相比，MOMFO的最优折衷解是最令人满意的，具有非常显著的优势，MOMFO在解决电力系统优化调度问题上具有较大竞争力。

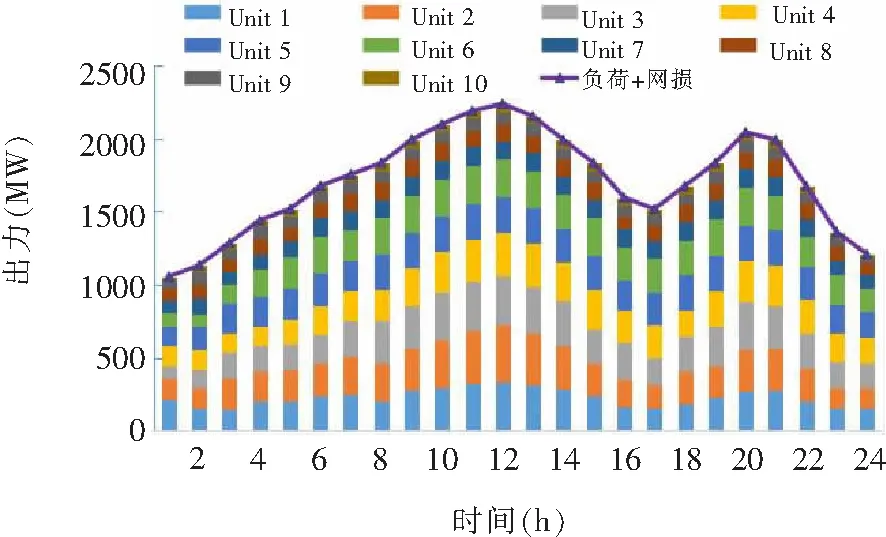
图5 各机组出力情况

表2 结果对比

4.2 Case2：修改后的IEEE 39节点系统

取修改的IEEE 39节点系统作为虚拟电厂参与下含高渗透可再生能源的双层优化调度模型，系统由10台常规机组与46条传输线路组成；风电场与光伏电站分别由1、3节点接入；负荷、送端风电出力预测均值见图6，VPP运营利润及运行成本见表3；机组燃料系数与Case1一致；可再生能源直接/惩罚/存储成本系数见表4；多目标算法设置与Case1相同。常规机组开关机状态见图7，“o”为开机，“*”为关机；出力情况见图8；VPP调控计划见图9。

图6 系统负荷及风电、光伏出力预测

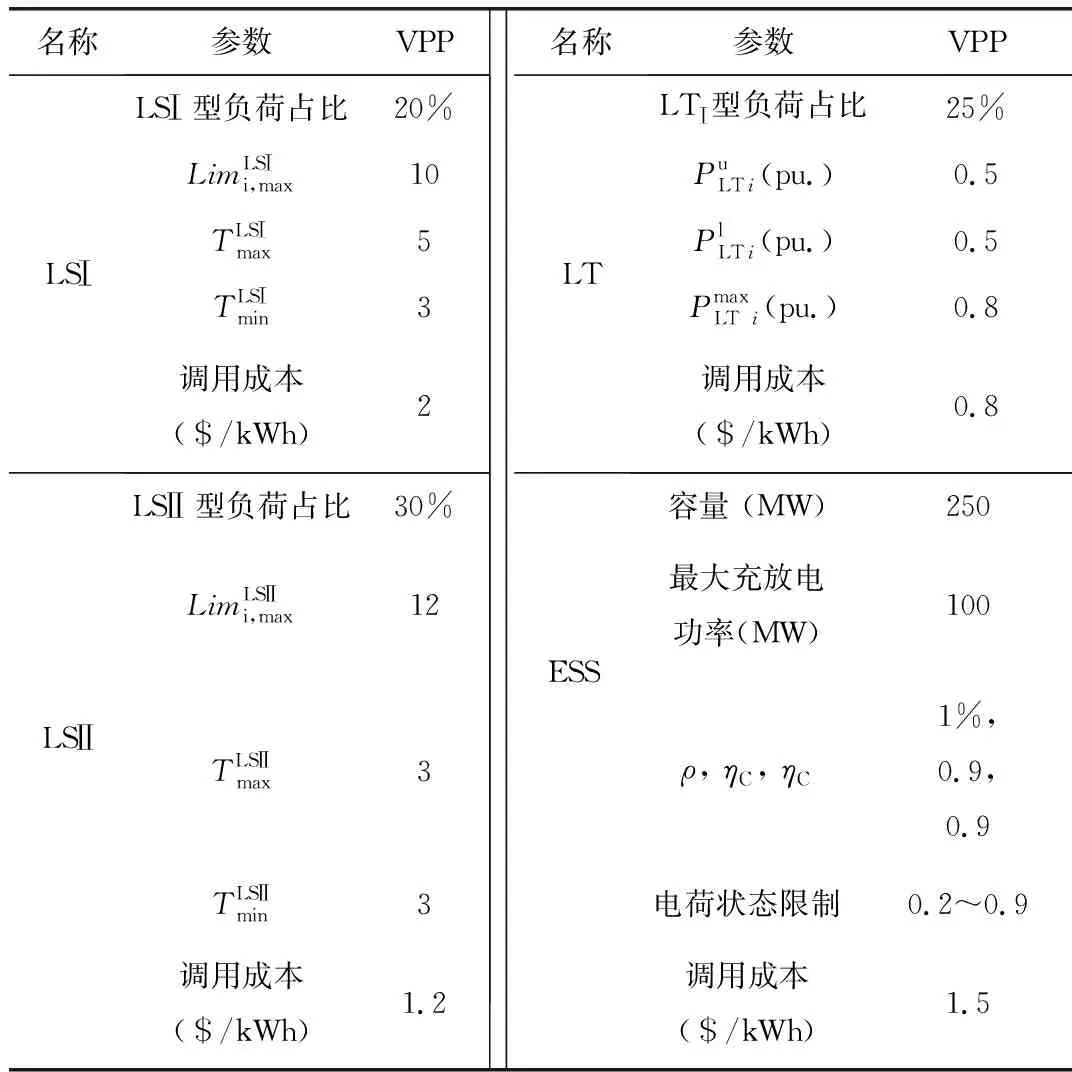
表3 虚拟电厂运行参数

表4 可再生能源直接/惩罚/存储成本系数

比较图5与图8可看出常规机组的发电量大幅度减小，使系统经济性得到提升；同时VPP在总调度周期内的调控变化趋势与系统内负荷的波动趋势基本一致，在系统负荷较高的时候，VPP整合区域内可控资源使得需求侧参与优化调度，维持系统电量平衡，降低常规机组出力，在提高系统经济性的同时减少污染排放，促进电力系统的可持续性发展。

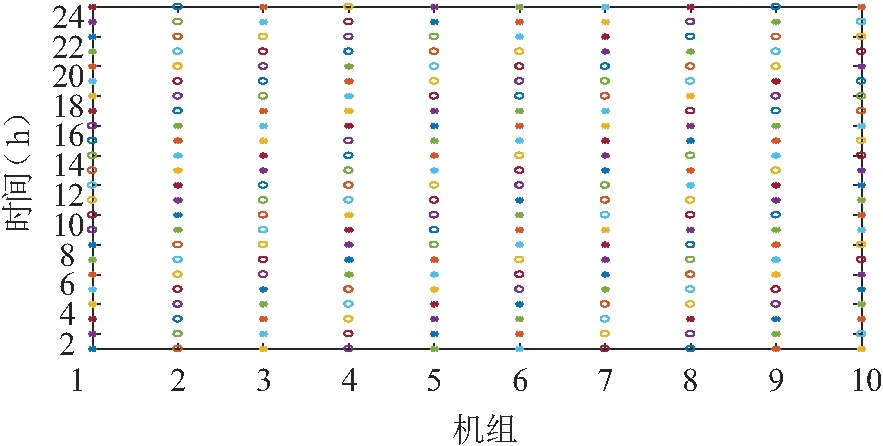
图7 常规机组开关机状态

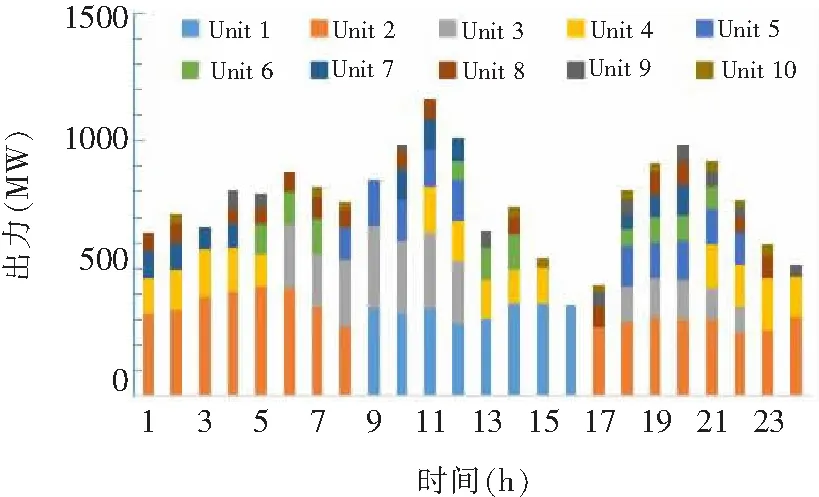
图8 常规机组出力情况

为探究不同规模可再生能源并网对系统调度结果的影响，风电与光伏规模分别取预测值得0.5～2.5倍，其系统成本见表5，VPP调控计划见图9。

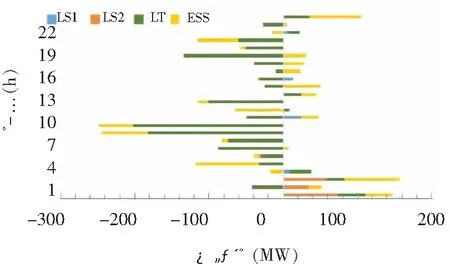
图9 VPP调控计划

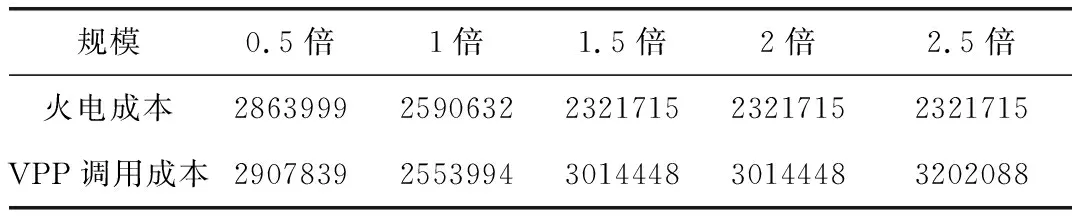
表5 不同可再生能源规模下的系统总成本

由图10可得，随着接入的可再生能源规模不断扩大，位于横坐标轴O点左侧的条形面积不断减小，相应右侧面积不断增大，说明系统对VPP的调度由向其吸收电量转变为注入电量，VPP可分担在传统电力系统中火电机组对可再生能源的备用，减少火电成本。同时表5结果也说明，随着可再生能源规模不断扩大，火电成本不断降低，系统经济性提高，环境污染问题得到改善。但由于可再生能源的大规模接入，系统的不确定性增加，VPP对可控资源调控比增加，VPP调用成本随之增加，其结果与图10相符。该结果对不同可再生能源渗透率下的虚拟电厂内部资源配置具有一定理论指导意义。

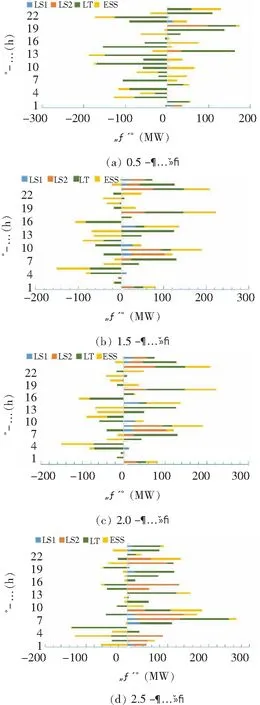
图10 不同可再生能源规模下的VPP调控计划

5 结束语

针对灵活控制分布式可再生能源与可控负荷参与系统市场交易和优化调度,文中提出一种虚拟电厂参与下含高渗透可再生能源系统的双层优化调度模型，根据虚拟电厂运营体系采用双层多目标优化对其进行建模，其中电网系统位于模型上层，虚拟电厂位于下层，两层之间交替求解实现协同调度。并且利用一种新颖的MOMFO对模型进行求解，算例证明了模型的可行性与算法的有效性。

提出的虚拟电厂参与下含高渗透可再生能源运行优化模型，在后续研究中可考虑电动汽车等更多类型；同时在日前组合优化结果的基础上，考虑弃风成本建立超短期调度模型，更加细致地描述各不确定变量的波动性,得到更加符合实际的调度运行方案，并且在实际问题上得到应用也是后续研究的重点。