计及深度调峰与一次调频的风火负荷优化分配

刘鑫，王康平，郭相阳，曲立楠，张巍，缪辉

(1. 国家电网公司西北分部， 西安 710048； 2.中国电力科学研究院有限公司， 南京 210003；3. 上海理工大学， 上海 200093)

0 引 言

新能源发电具有间歇性、随机性、反调峰性等特点[1]。随着新能源在电力系统中渗透率的增加，对电力系统的调频、调峰能力的需求也逐渐增加，提高系统的调峰调频能力也是提高新能源消纳能力的必然要求。

火电的灵活性改造是提升系统调峰能力和消纳弃风能力的重要手段[2]。若火电机组只参与基本调峰，则系统往往无法抑制大规模风电机组的大波动，使弃风量变大，成本变高。为能消纳更多的风电，减少弃风量，火电机组应具备深度调峰能力。2018年国家发改委、国家能源局联合印发了《关于提升电力系统调节能力的指导意见》，提出了“十三五”期间加快推进能源的供给侧结构改革。主要通过机组的外部改造或者内部改造提高机组的调峰幅度和爬坡能力完成2.2亿千瓦的火电机组灵活性改造。文献[3]提出对电锅炉系统的供热方案进行改造,可在一定程度上实现火电机组的运行灵活性，提高火电机组调峰能力。文献[4]针对双馈风电场与直驱风电场并联接入含固定串补系统的次同步振荡问题,建立了混合风电场线性化模型，分析风机占比、控制参数和运行风速对系统运行性的影响，进一步提高了电网安全性。

通过使风电机组具备一次调频功能，协同火电机组共同参与电力系统的一次调频，可以提高系统调频能力，提升风电消纳能力[5-7]。风电机组的主要调频技术有转子动能控制和桨距角控制两种。转子动能控制又分为下垂控制、虚拟惯性控制两种模式。前者通过模拟同步发电机一次调频的功-频静态特性曲线，根据频率偏差去调节风机的有功出力；而后者控制依据频率变化率来调节风电机组的有功指令。桨距角控制是通过调整风机的桨距角来改变风机捕获的风能，使风电偏离最大功率点跟踪曲线。由于风电参与调频速度快、持续时间短，而火电调频持续时间久，所以风火联合调频以火电为主、风电为辅。文献[8]提出了一种改进的风机分组优化和功率分配策略，充分利用风电调频容量，改善系统的频率特性。同时，为了防止当风电机组退出调频而对系统频率造成二次跌宕时，可配置风机转速延时恢复模块[9]。

当风电机组出力较大时，火电机组需参与深度调峰以减少弃风量，会导致其出力区间下降，而调频能力与火电机组的运行区间相关，使火电机组调频能力降低，进而造成系统的一次调频备用不足。风电机组参与一次调频能够很好地弥补这一缺点[10]。由上述分析可得，在日前调度中将电网中的负荷合理分配给各机组，不仅能优化电网的经济收益而且能确保有充裕的调频能力。然而，过往的研究仅考虑火电机组参与一次调频的条件下如何分配运行负荷以达到最佳效果[11-12]。

基于此，文章首先考虑火电参与深度调峰，得到火电在不同负荷区间的一次调频能力；然后对风电机组的一次调频能力与反调峰特性进行分析，并进一步提出了风火联合参与一次调频场景下的日前负荷分配模型。通过鲁棒优化模型刻画预测风速与负荷波动的情况下最优的负荷分配方案，最后通过算例结果证明了所提出模型的有效性和正确性。

1 常规机组的调峰与调频能力模型

随着电网中风电渗透率的升高，其反调峰特性对于电网的影响加剧。为尽可能减少大量弃风发生，火电机组将进行深度调峰改造以提高系统在负荷低谷时的调峰能力，然而火电参与深度调峰势必造成其一次调频能力下降。本节将探讨常规火电机组的调峰能力、一次调频能力以及两者之间的关系。

1.1 考虑深度调峰的火电机组调峰模型

火电机组调峰划分为三个过程，除基本调峰外，还包括不投油和投油的深度调峰部分[13]。设定PTN为额定功率，PTa为基本调峰的下限值，PTb为不投油深度调峰的下限值，PTc为投油深度调峰的下限值。通常情况下：PTa=(40%～50%)PTN，PTb=35%PTN。

在火电机组参与基本调峰时，运行成本主要包括煤耗成本与环境成本。对于煤耗成本，随着负荷的减少，火电机组的运行工况越偏离额定时，其供电煤耗率越高，煤耗成本也相应增加。假设日前调度的时间尺度Δt=1 h，t为整点时刻的集合，火电机组的煤耗成本如式(1)所示：

cT(i)]Δt

(1)

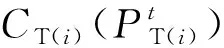
另一方面，火电机组运行所造成的环境污染需要缴纳环境成本gT(i)， 如式(2)所示：

(2)

式中ξn为污染物排放的单位价格；VT(i)为第i台机组额定运行时的烟气排放量；αT(i)、βT(i)、γT(i)、λT(i)分别为第i台火电机组的排污成本特性系数。

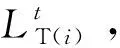
(3)

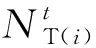
当机组处于投油深度调峰时，除煤耗成本、环境成本与转子寿命成本外，还需考虑其投油成本，计算如式(4)所示：

(4)

1.2 火电机组的一次调频能力

火电机组的一次调频能力是通过调节阀具有一定节流裕度的滑压运行方式来实现的。故可以通过改变调节阀的开度裕量，来控制火电机组的一次调频能力，裕量值越高，火电机组的调频能力越强。在实际运行中，利用给水旁路协同调节阀门使用，亦可达到与增大调节阀节流相似的效果。

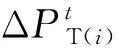
(5)

火电机组参与一次调频的功率同样会增加运行成本，包含煤耗成本与环境成本。式(6)为考虑调峰与一次调频的火电机组出力。

(6)

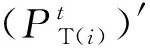
(7)

2 风电机组的一次调频能力与反调峰特性

风电机组参与一次调频能够有效缓解由火电机组参与深度调峰而导致的系统调频能力下降。与此同时，由于风电机组预留备用容量参与调频，其反调峰特性对于系统的调峰压力也进一步减弱。本节将分析风电机组的一次调频能力及其反调峰特性，并分析两者间的联系。

2.1 风电机组的一次调频能力

风电机组不能像火电机组一样持续稳定地参与系统调频，由于风速的预测间隔为15 min，故设定在时间尺Δτ=15 min内，风速均采用上一时刻的预测值，即认为风机捕获的风能保持不变。

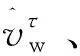
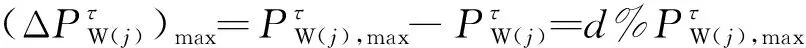
(8)

(9)

式(9)中的系数k0定义为：

(10)

式中ρ为大气密度；A为风轮叶片扫过的面积；Cpmax为风电机组的最大风能捕获系数。

假设参与调频的风电机组的调节限幅系数为10%，出力死区设定为额定容量的10%，则定义风机j的最小出力决策变量λW(j)如式(11)所示：

(11)

式中,当λW(j)=0时，风电机组无有功备用容量，不具有一次调频能力；当λW(j)=1时，风电机组具有充足的备用容量；当0<λW(j)<1时，风电机组具有一定的有功备用容量。考虑到风机出力死区，故风机具有一次调频能力的出力为0.1PW(j),N。

(12)

(13)

2.2 风电机组的反调峰特性

在电网处于负荷低谷时，风电的发电量通常较高，给系统调峰带来较大压力；若部分风电机组参与一次调频时，风电机组的总发电功率将减少以留出备用容量，一定程度上削弱了其反调峰特性对于电网的影响。式(14)分别给出了参与和不参与一次调频的风电机组对于电网调峰压力的影响。

(14)

(15)

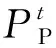
(16)

(17)

式中mW为风电的发电售价。

3 考虑调峰调频风火联合负荷分配模型

本节将简要分析部分火电机组参与深度调峰与部分风电机组参与一次调频对于全网的调峰与调频的影响，并提出相应的负荷分配模型。基于上述分析，给出系统成本最小化为目标函数及其约束函数。为考虑风速与负荷的不确定性，将具有保守度参数的单层鲁棒优化算法求解引入负荷分配模型。最后在MATLAB环境下使用CPLEX软件求解该单层模型。

3.1 考虑风火联合调峰调频的日前负荷分配模型

通过第一节对于火电机组的调峰能力与一次调频能力的分析，火电机组处于深度调峰时，其日前计划发电功率较小，相应的一次调频能力较于基本调峰时有明显下降。由第二节中对于风电机组的调频能力与反调峰特性的分析，在负荷分配中，风电机组为一次调频预留的备用容量越大，其反调峰特性对于电网的影响越小。由于风电的一次调频能力是基于时间尺度Δτ，而火电的一次调频能力较为稳定，时间尺度为Δt，故需建立两种时间尺度下的联系。式(18)为风火联合提供的一次调频能力。

(18)

上述分析对火电与风电各自参与调峰与调频的关系进行了总结。然而，风电与火电两种资源之间调峰调频备用容量也存在相互的影响。在2.2小节对于风电反调峰特性的分析中，提及了风电的反调峰特性对于火电机组调峰能力的影响，简要归纳为：风电的计划发电量超出负荷预测量越小，弃风量或火电调峰深度也就越浅。综合风火各自的调峰调频间的关系以及风火之间调峰调频容量的影响，最终得到四步骤如图1所示。

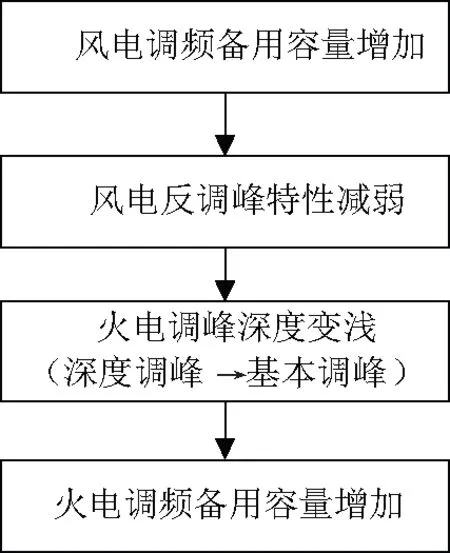
图1 风火联合参与调峰调频的连锁模型

火电的深度调峰改造确保火电机组的可下探的调峰深度充足，而风电参与一次调频能够降低日前计划的调峰深度以减少运行成本；并且当部分参与深度调峰的火电机组变为基本调峰时，其一次调频能力也会增强。在调峰压力巨大的区域电网中，即使改造后火电机组参与深度调峰可能也无法完全保证电网的调峰需求，并且系统的一次调频能力也会有所下降；而将风电机组参与一次调频纳入负荷分配中可以一定程度上降低电网的调频与调峰压力，进而减少由调峰容量的不足所造成的弃风。

通过对两种情况的分析，火电机组的深度改造与风电参与一次调频能够有效地减少全网的弃风量与运行成本，增加调频能力。图2为基于连锁模型得到的最优负荷分配模型，其优化目标设定为弃风成本与运行成本之和最小。

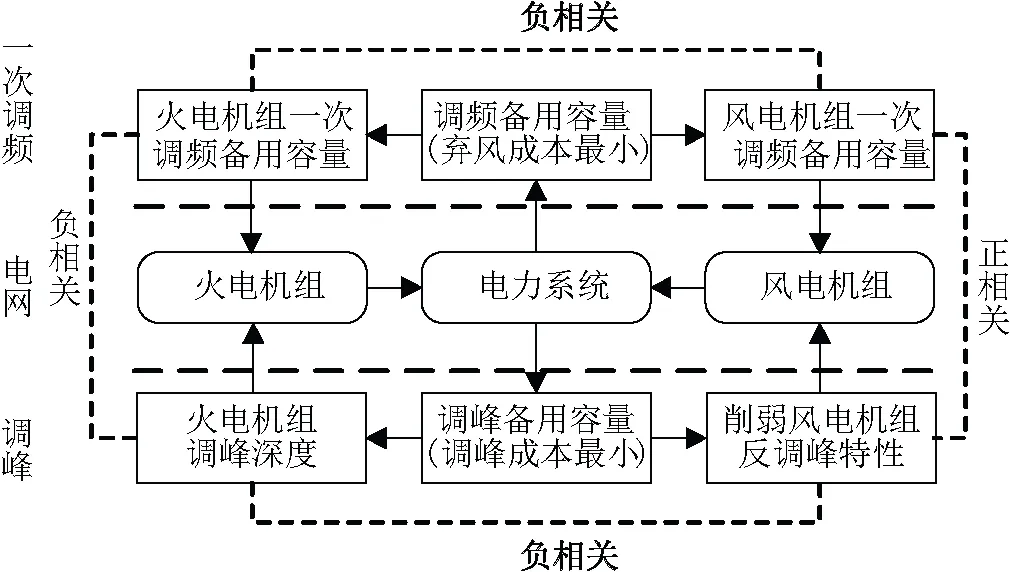
图2 考虑风火联合调峰调频的负荷分配模型

3.2 优化目标与约束条件

根据3.1节中的分析，目标函数被设定为弃风成本与机组运行成本之和最小，各成本均已在1、2节中进行了分析，目标函数如下：

(19)

每个计划周期内的约束函数由出力约束，机组爬坡约束，一次调频能力约束组成。

(1)风火机组出力平衡约束。

(20)

(21)

式(20)为负荷预测值对风火出力的约束；式(21)为风电机组与火电机组的出力上下限约束。

(2)机组爬坡能力约束。

(22)

(3)一次调频能力约束。

系统的调频能力必须满足电网的调频需求：

(23)

式中 ΔPR为当前系统所需的一次容量，该值为电网总装机容量的3%～5%。

3.3 鲁棒优化算法

在3.2节的目标函数中，成本与实际风速和实际负荷量相关，而实际风速/负荷量通常是基于预测风速/负荷量波动的，被称为不确定变量。若采用预测风速/负荷量作为输入变量，则得到的优化结果可能并非实际运行时的最优负荷分配模型。为减少预测值与实际值的误差，引入了鲁棒优化算法以刻画预测值与实际值的误差[17-18]。

假设上述不确定变量的实际值的波动范围为预测值上下对称浮动，风速与负荷的取值范围满足式(24)～式(25)所示的约束。

(24)

(25)

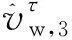
由于无法得到实际场景下确切的风速与负荷量，故该鲁棒优化模型为双阶段，如式(26)所示的max-min问题。

(26)

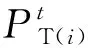
当风速三次方取其预测范围的下限而负荷量取其预测值的上限时，优化结果将会过于保守，故将引入保守度Γ1、Γ2控制鲁棒优化算法的不确定性。风速与负荷量需满足如下约束：

(27)

(28)

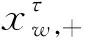
保守度Γ∈{Γ1,Γ2}被用于调节结果的最优性与算法鲁棒性之间的平衡。当Γ=0时，意味着鲁棒优化中不考虑不确定变量的波动，此时的模型等价于传统调度模型。当Γ=96时，该模型考虑了所有极端场景，其鲁棒性程度最高，优化结果最为保守。综上所述，考虑调峰调频的风火联合负荷分配模型如式(29)所示:

(29)

针对式(29)所得的max-min模型，利用对偶原理将双层目标函数转化为单层目标函数，利用分段线性化方法将凸函数进行变换[19]，并采用Big-M法将模型变化为线规划问题。最后在MATLAB环境下利用CPLEX软件求解该线性规划问题的最优解，具体求法参考文献[20]。

4 算例分析

对比不同风电渗透率下对于电网调频调峰的影响。假定风火系统的总装机容量被设定为4 000 MW，仿真将在以下两种场景中进行。

(1)场景1：风电渗透率为30%。

火电机组总容量为2 800 MW，由1台1 000 MW机组与3台600 MW机组组成。风电机组的总容量为1 200 MW，由800台1.5 MW的风电机组组成。

(2)场景2：风电渗透率为50%。

火电机组总容量为2 000 MW，由2台1 000 MW机组组成。风电机组的总容量约为2 000 MW，由1 333台1.5 MW的风电机组组成。

在上述两类场景中，1 000 MW与600 MW的火电机组的基本参数如表1所示，并且均已完成深度调峰改造。两类火电机组在不同负荷段下的一次调频能力分别为ΔPT,600、ΔPT,1000[12]，如式(30)、式(31)所示；设定煤炭的单位价格ξcoal为680元/t，火电机组的烟气排放量VT(i)为400 万·m3/h，污染物排放的单位价格ξn为500 元/t。

表1 火电机组相关计算参数

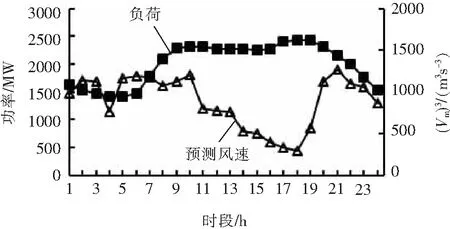
图3 负荷与风速预测值

(30)

(31)

为研究不同风电渗透率对于考虑调峰调频对负荷分配的影响，算例1中设置了渗透率为30%与50%，得到各个时刻火电机组与风电机组的出力与一次调频备用容量如图4所示。

图4 不同渗透率下各机组发电曲线与

由图4(a)、图4(b)可得30%风电渗透率下的结论：当风速接近高风速的时段而负荷量较低的时段(0～28时段与88～96时段)，火电机组均处于深度调峰阶段，风电机组的一次调频备用在该时段调频需求中的占比较高。风电机组参与调频有效避免了弃风现象的发生，削弱了其反调峰特性，并且弥补了由于火电机组深度调峰所带来的一次调频能力的不足。在风速与负荷量均较高的时段(28～40时段与76～88时段)，火电机组处于基本调峰阶段，其一次调频备用增加，风电机组一次调频备用占比下降(约为60%左右)。在风速逐渐降低并接近中风速下限而负荷量较高的时段(40～76时段)，火电机组的计划发电功率较高，一次调频备用增加，风电机组一次调频备用占比降低。在全时段内，风电机组一次调频备用占风机计划总出力的7.7%左右，占系统调频总量的52%。

对比图4(a)、图4(b)与图4(c)、图4(d)两组渗透率下的数据可得以下结论：

(1)50%渗透率下火电机组处于深度调峰阶段的时段明显变长，如28～40时段与76～88时段内，火电机组处于深度调峰阶段，且部分时段出现了弃风现象，约占风电机组总出力的16%；

(2)在风速逐渐降低接近中风速下限而负荷量较高的时间段内，由于风电机组总装机容量的增加及火电装机容量减少，导致火电的计划发电功率相较原来有明显下滑；

(3)相较于30%渗透率下，50%渗透率下风电的一次调频备用增加以削弱风电的反调峰特性，减少弃风量，约占系统调频总量的61%，占风机计划总出力的5.1%左右。

综上所述，所提出的风火联合调峰调频的负荷分配方案能够在较高的风电渗透率下(30%)避免弃风现象的发生，并且能够弥补火电机组调频能力的不足；而在极端风电渗透率下(50%)通过增加风电一次调频备用，减少电网的弃风量，缓解系统的调峰压力。两种渗透率下的弃风成本与运行成本如表2所示。

表2 不同渗透率下的弃风成本与运行成本

由表2可知，50%下弃风成本相较于30%下大幅增加；而运行成本却有所减少，主要原因在于火电机组装机容量大幅减少，而平均运行成本实际上是增加的。

5 结束语

基于新能源渗透率不断增加的背景下，研究了火电机组经过深度改造与风电机组参与一次调频对于负荷分配方案制定的影响。根据对火电机组、风电机组以及两者之间调峰调频能力相互制约的分析，制定了考虑调峰调频的风火联合负荷优化分配模型，以弃风成本与机组运行成本之和为目标函数求其最优负荷分配模型。引入鲁棒优化模型以刻画风速和负荷的不确定性，并转化为线性模型求解。最后以风火总装机容量4 000 MW下不同风电渗透率进行仿真分析，结果表明该模型不仅能保证系统有足够的调频裕度，而且还能缓解系统调峰压力,尽可能减少弃风量。