新型柔性限高架动力分析
朱文彬, 罗 辉
(1. 中南安全环境技术研究院股份有限公司, 湖北 武汉 430051;2. 华中科技大学 土木与水利工程学院, 湖北 武汉 430074)
目前,我国国内限高架根据其结构形式,主要可分为刚性限高架、智能限高架、柔性限高架三大类。其中柔性限高架是指采用缓冲装置或柔性吸能材料降低撞击力,因其可以给予司机刹车的反应时间,降低架乘人员风险,减少对车辆、限高架横梁的破坏而被广泛应用。
郝珊珊[1]提出一种带橡胶缓冲装置的半刚性节点的限高架,通过有限元模拟发现,限高架动力响应的峰值减小,峰值出现的时间延后,车辆塑性变形减少,验证了橡胶缓冲装置有良好的缓冲吸能作用,半刚性节点有良好的耗能作用。王金田[2]研究了考虑土 - 结构相互作用下的车辆与限高架碰撞动力响应,通过有限元模拟,对比柱底固结和考虑土 - 结构相互作用两种条件下碰撞初速度、车辆质量、土弹性模量等因素对限高架动力响应的影响。Wang等[3]对超高卡车与限高保护架的碰撞过程进行了仿真,并从变形、应力,载荷等方面分析了限高架的失效机理。荷载分析结果表明,最大冲击力大约与初始速度成正比,可用于选择设计中的碰撞荷载。应力分析结果表明,最大应力通常发生在保护框横杆和接缝区域。增加对角撑杆或增加横杆厚度是提高保护框架抗冲击能力的有效方法。鞠翱天等[4,5]研究了车辆撞击下钢管混凝土限高架的动力响应,并与钢管限高架对比,发现钢管混凝土限高架的撞击力均值更大,位移更小,且随着钢管壁厚的增加和核心混凝土强度的增加,平均撞击力会增大,撞击面的位移会减小。
综上所述,目前国内外专家学者对柔性限高架碰撞问题的研究有一定成果,但对于碰撞机理(如碰撞力大小、缓冲装置的吸能耗能机理等)的研究仍然不足,导致在实际工程中对限高架防撞措施设计的有效指导和防撞效果的准确评价缺乏科学依据。大部分研究仅停留在理论阶段,未考虑实际工程问题,存在结构复杂、成本较高、制作运输安装困难等问题。
本文以“以人为本”为设计理念,提出一种基于刚性限高架改装的新型装配式柔性限高架,配置有橡胶缓冲层、弹簧铰支座、横梁薄弱点三级防护措施,减小超高车辆与限高架撞击事故造成的损伤。并利用LS-DYNA对车辆与柔性限高架的碰撞过程进行有限元模拟,分析其动力响应特征,并与刚性限高架对比,分析柔性限高架三级防护措施的作用。
1 新型柔性限高架设计
本文提出一种基于刚性限高架改装的新型装配式柔性限高架。螺栓连接的装配式结构方便运输、安装和维护。限高架整体结构由单层框架结构改为双层框架结构,第一层为抗撞击横梁,第二层横梁可增加结构纵向刚度,同时可悬挂交通提示牌,并在第一层抗撞击横梁上设置橡胶缓冲层、弹簧铰支座、横梁薄弱点三级防护措施。整体限高架外观三维图与实物图如图1所示。
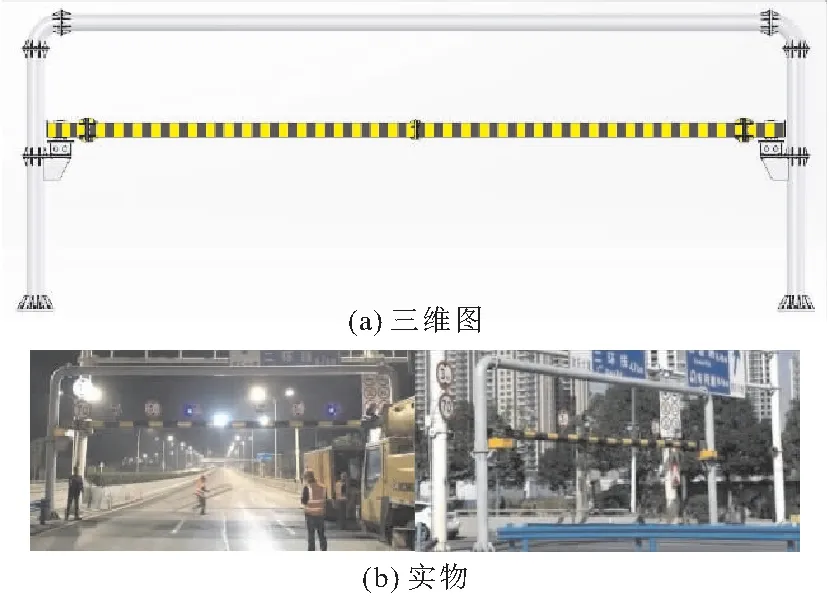
图1 新型柔性限高架外观
1.1 部件选型
1.1.1 立柱
新型柔性限高架立柱为与刚性限高架截面尺寸相同的单排圆柱。如图2所示。立柱中部需焊接牛腿,用于弹簧铰支座的安装,柱顶与上层横梁通过弯管和螺栓连接,柱底与基础通过螺栓连接。

图2 新型柔性限高架立柱三维图
1.1.2 横梁、橡胶缓冲块及薄弱点
缓冲橡胶块厚度为250 mm,撞击面为半圆形,与横梁之间通过螺栓连接,为减轻橡胶自重,将橡胶缓冲块内部挖空,厚度为50 mm。进行重力作用下的静力验算,薄弱点断开前,横梁跨中挠度为7.4 mm,薄弱点断开后挠度为16.4 mm,均满足设计要求。
横梁跨中薄弱点可通过焊接或螺栓连接,但焊接质量人为因素影响较大,不易控制,所以选择在梁端焊接端板,以螺栓作为薄弱点连接方式,如图3所示。

图3 横梁、缓冲橡胶块、薄弱点外观及其连接
1.1.3 弹簧铰支座
弹簧铰支座是柔性限高架中最复杂的构件,作为横梁与立柱的连接构件,必须具备足够的强度和稳定性,作为吸能构件,必须设置合理的参数。其上板通过销轴与横梁端部连接,下板通过螺栓与牛腿连接,上板与下板通过两根50CrVA高碳钢弹簧连接,增加稳定性,如图4所示。支座压缩行程理论上越大越好,但受限于制作工艺和安装空间,最终定为0.4 m。弹簧刚度设置为100 kN/m。

图4 弹簧铰支座外观
2 有限元模型
2.1 车辆有限元模型
车辆与限高架撞击事故带来了巨大的经济损失和安全风险。其中,大中型客运车、公交车由于车内载客人数较多,尤其是市内公交车,没有乘员约束系统对乘客进行保护,一旦发生与限高架相撞事故,会造成车辆乘员受伤甚至死亡,事故车辆和限高架的损伤也会使服役周期大大缩短甚至报废。
本文以公交车作为碰撞车辆,所用车辆有限元模型为NCAC模型数据库中选取的一辆半承载式客车[6],车辆模型如图5所示。半承载式客车相比于全承载式客车,以底盘大梁作为车辆主要承重构件,前围框架、侧围框架等碰撞区域主要构件的强度均更弱,在碰撞事故中损伤更严重。车辆几何尺寸为长12.45 m,宽2.5 m,高3.13 m,轴距6.425 m,整车质量为13.74 t。车辆与限高架撞击的主要构件前围车架是50 mm×50 mm×3 mm的Q235方钢管。撞击高度设置在车顶以下0.6 m处,模拟超高大中型客运车、双层公交车与限高架的碰撞。

图5 车辆有限元模型
目前武汉市公交车的限速为45 km/h,本文以最大速度的80%(即10 m/s)[7]设置模型车辆的基准速度。
2.2 柔性限高架有限元模型
2.2.1 模型假定
为建立柔性限高架有限元模型(图6),在保证计算精度条件下提高计算速度,作出如下假设和简化:
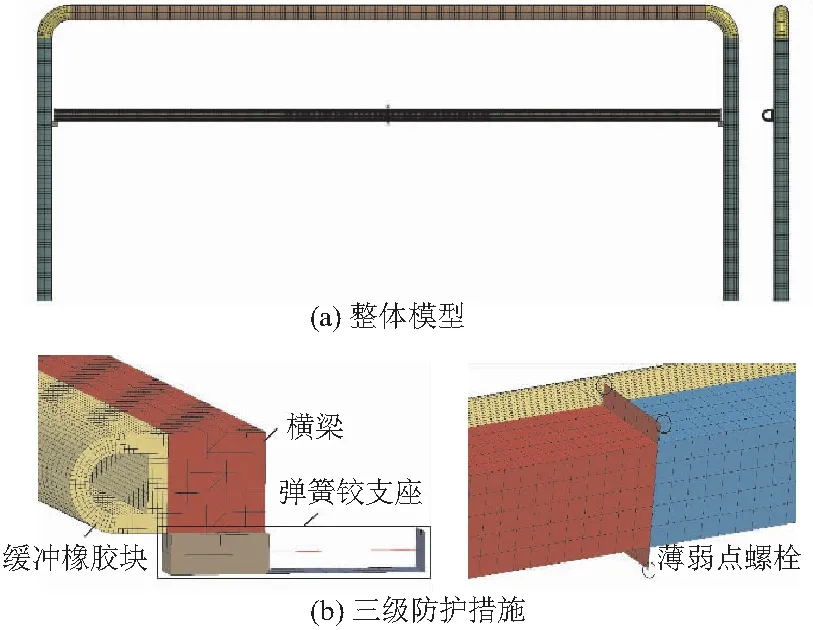
图6 柔性限高架有限元模型
(1) 限高架立柱与混凝土基础连接可靠,立柱与基础固接;
(2)不考虑土体与结构的相互作用,完全约束柱底自由度;
(3) 立柱与横梁连接可靠,模型中不建立螺栓和法兰盘,对连接截面进行刚化处理;
(4) 立柱与牛腿焊接牢固,考虑牛腿对立柱的强化作用,对连接截面进行刚化处理。
2.2.2 单元类型及连接
限高架立柱、横梁使用壳单元模拟,车辆和限高架撞击区域的构件采用4节点Belytschko-Tsay全积分壳单元,非撞击区域构件采用4节点Belytschko-Tsay缩减积分壳单元,在厚度方向选取等距离分布的5个积分点,考虑壳单元的厚度变化,使材料产生大变形时有更好的精度。
缓冲橡胶块使用8节点常应力缩减积分实体单元,有更好的计算稳定性。为控制缩减积分实体单元的沙漏能,增加撞击区域的网格密度,并设置对实体单元体积精确积分的Flanagan-Belytschko刚度沙漏控制算法。
弹簧铰支座由3部分构成,如图7a所示。限高架横梁端部焊有端板,有限元模型中设置截面刚化,构成刚体1,弹簧铰支座套筒内的活塞为刚体2,立柱上的牛腿为刚体3。刚体1,2之间设为铰接;刚体2,3之间通过弹簧连接,且需要限制2个刚体之间除弹簧轴向以外的自由度。通过旋转铰、滑移铰、弹簧单元完整模拟出弹簧铰支座的实际受力情况。
弹簧铰支座的弹簧在达到最大压缩行程后,弹簧活塞会与套筒底部缓冲层直接接触传力。本文有限元模型中不建立套筒和缓冲层的实体模型,通过刚度突变的非线性弹簧来模拟弹簧铰支座的极限状态。采用能精确模拟刚度突变弹簧的非线性离散梁单元*BEAM_TYPE6。设置的非线性弹簧刚度曲线如图7b所示,0.4 m压缩行程内的刚度为100 kN/m,超过此范围的变形会产生较大回复力,使活塞从运动到静止平稳过渡,模拟弹簧铰支座套筒内活塞与筒底缓冲层的撞击。
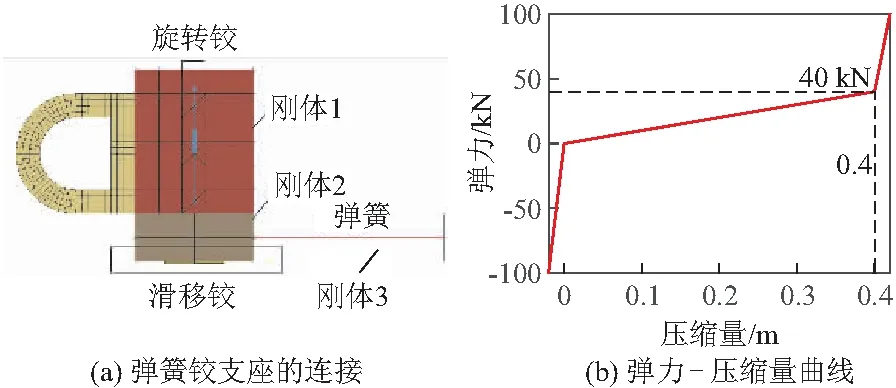
图7 弹簧铰支座的连接及弹力曲线
横梁分为2段,连接处焊接端板,通过截面刚化模拟端板,2段横梁通过端板四角的4个螺栓连接,如图8所示。其极限状态是由撞击背面的2个受拉螺栓控制,受拉螺栓达到极限状态断开后,跨中截面的应力重分配会导致其他螺栓应力迅速增加,达到极限状态也随即断开。因此,有限元模型中进行部分简化,不设置横梁端板的接触,以靠近撞击面的螺栓承受横梁变形时产生的压力。采用可变形、可连接刚体的焊接梁单元*BEAM_TYPE9模拟螺栓,设置较大弹性模量和截面面积,模拟实际安装时的预紧力对螺栓变形的限制,且不影响螺栓轴力、剪力数据的提取和破坏准则的设置。
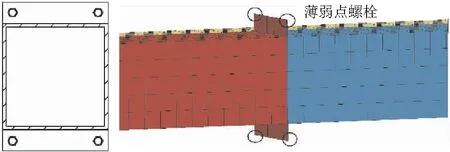
图8 横梁跨中薄弱点
2.3 材料本构模型
柔性限高架的主要材料为Q345钢材,使用Cowper-Symonds本构模型进行模拟,相关性能参数如表1所示,通过拉伸试验测得钢材静力应力 - 应变曲线,而后将测得工程应力 - 应变转换为真实应力 - 应变曲线[8,9],如图9所示橡胶采用Mooney-Rivlin本构模型进行描述,LS-DYNA中已提供基于Mooney-Rivlin本构的橡胶材料模型,根据文献[10]设置橡胶材料的参数。
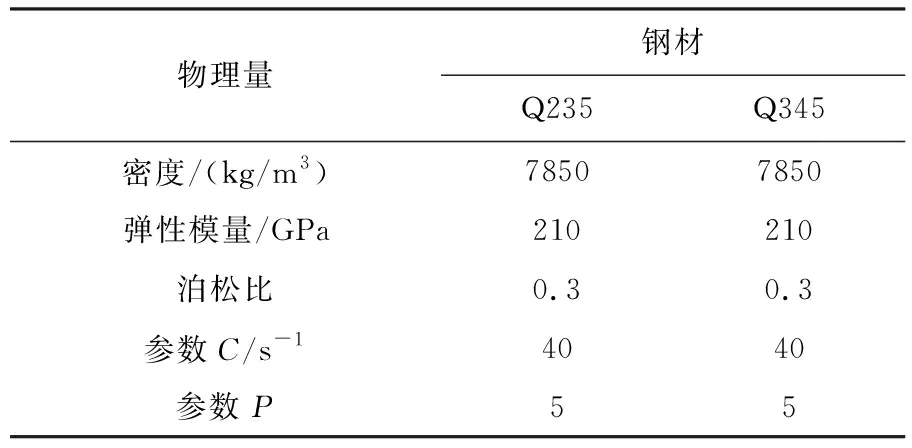
表1 钢材的Cowper-Symonds本构模型参数
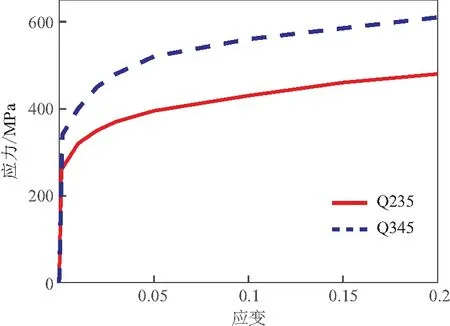
图9 Q235与Q345真实应力 - 应变曲线

表2 橡胶的Mooney-Rivlin本构模型参数
2.4 接触类型
LS-DYNA中提供多种接触类型,本文主要使用3种接触类型:
(1) 单面接触类型*AUTOMATIC_SINGLE _SURFACE,车辆内部各个构件的接触使用此类型;
(2)双面接触类型*AUTOMATIC_SURFACE_TO_SURFACE,车辆与减震橡胶块,车辆轮胎与地面的接触使用此类型。刚性限高架撞击工况中,车辆与减振橡胶块之间的动摩擦和静摩擦系数设置为0.3,不考虑车辆与地面摩擦力;
(3) 双面绑定接触类型*TIED_SURFACE_TO_SURFACE,缓冲橡胶块与横梁的接触使用此类型。
3 横梁薄弱点螺栓分析
横梁跨中薄弱点是保护车辆与限高架的重要防护措施,文献[10~12]通过试验研究得出结论,普通螺栓群中和轴的位置随着加载从端板形心附近移动到受压螺栓形心附近,螺栓群中螺栓排数越少,受拉螺栓断裂时中和轴越靠近最外排受压螺栓。因此本文以受压螺栓处作为中和轴位置来计算受拉螺栓轴力。
提取横梁跨中截面的内力,其中剪力较小,可忽略不计,根据轴力和弯矩计算螺栓的轴力,时程曲线如图10b所示。从图中可以看出,轴力达到第二峰值的时刻处于撞击力上升阶段,即薄弱点的设计破坏阶段。螺栓轴力出现明显阶段性变化,车辆与横梁的初始撞击导致出现第一峰值,支座弹簧达到极限行程后车辆与横梁的二次撞击导致出现第二峰值,也是最大值。由于前围框架与顶围框架在撞击过程中的屈曲变形对限高架横梁的挤压产生竖向向下的压力和自重作用,螺栓4比螺栓1的轴力稍大。因此,以螺栓4作为薄弱点控制螺栓,以轴力为破坏准则,最大轴力设置为第二峰值。
设置破坏准则后的螺栓轴力如图10c所示,从图中可以看出,以螺栓4的第二峰值设置破坏轴力后,首先螺栓4达到破坏轴力值后断开,轴力降为0,由于受力重分配,其他螺栓轴力迅速增加,达到破坏轴力值后断开。在后续计算中设置当螺栓出现第二峰值时薄弱点断开。
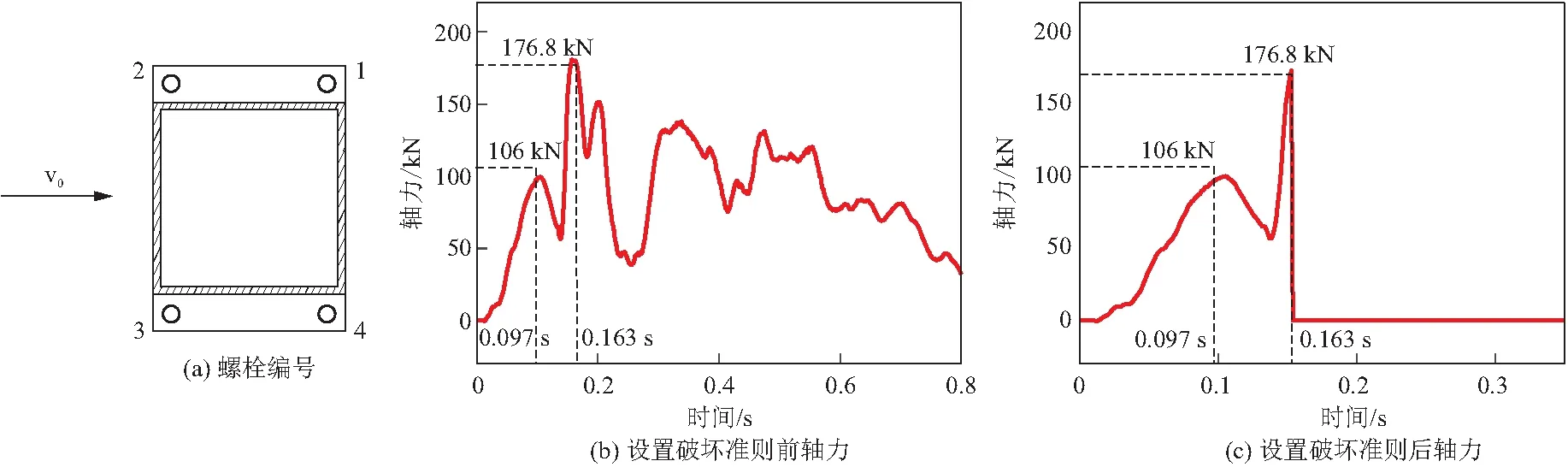
图10 横梁薄弱点4号螺栓轴力时程曲线
4 能量分析
限高架总能量、车辆总能量、限高架主要构件总能量变化曲线如图11~13所示。从图中可以看出,在开始撞击阶段,横梁随车辆的撞击开始移动,车辆动能主要转化为横梁的动能,限高架的各个构件内能变化较小。在此阶段,车辆动能下降和内能上升也较平缓。横梁的弹簧铰支座达到极限行程后,车辆与限高架发生二次碰撞,限高架和车辆的内能上升速度、车辆的动能下降速度开始增加。
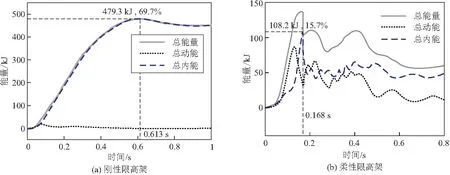
图11 限高架总能量变化曲线
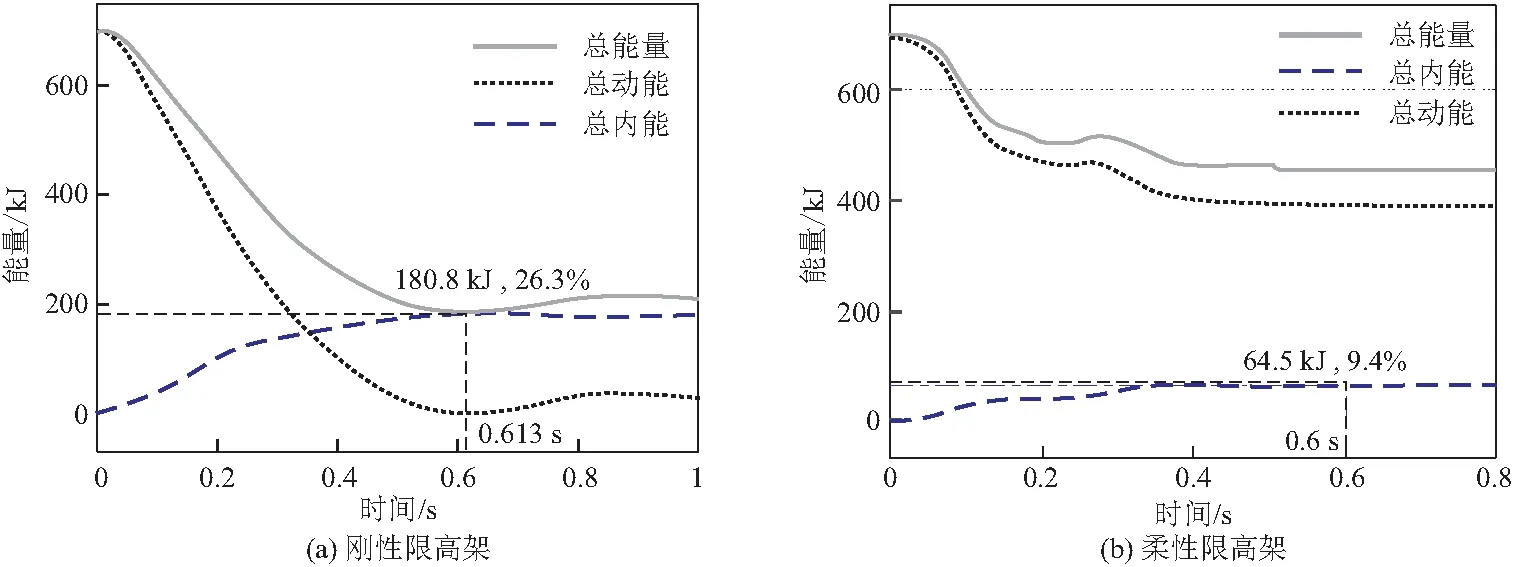
图12 车辆总能量变化曲线
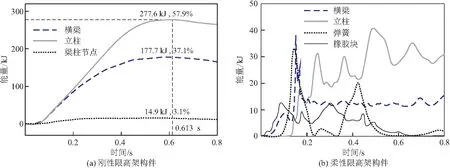
图13 限高架构件内能变化曲线
柔性限高架的横梁薄弱点断开后,结构阻尼使各构件的运动逐渐停止,各构件的动能短暂波动后逐渐降为0,总内能也维持在60 kJ左右,相比刚性限高架工况减少87.4%。其中,支座弹簧的内能有2处波动较大,分别在达到极限压缩行程时和横梁断开后反弹触底时,这与前文中弹簧的变刚度设定有关,实际结构中这部分能量应该分配到横梁与立柱。横梁断开后处于悬挑状态,重力作用下增加立柱的变形,与立柱自身的振动叠加,导致立柱内能的波动状态。
在横梁薄弱点断开后,车辆与横梁仍有一段接触时间,造成能量出现短暂变化,然后趋于平稳。最终车辆的动能减少34.6%,内能为64.5 kJ,与刚性限高架工况中的180.8 kJ相比减少64.3%。
综上所述,设置两级防护措施的柔性限高架,在撞击初始阶段,撞击导致的车辆和限高架损伤相比于刚性限高架更小,但在后期阶段,限高架吸收的能量释放,车辆的损伤会增加。而设置三级防护措施的柔性限高架,横梁在车辆损伤增加的过程中断开,车辆安全通过,达到限高架和车辆损伤均较小的平衡状态。
5 变形和内力分析
5.1 限高架变形和内力分析
柔性限高架应力在遭受撞击而致薄弱点断开云图如图14所示。限高架在薄弱点断开前时刻,横梁跨中应力达到最大,薄弱点断开后,横梁应力迅速释放,横梁在车辆撞击作用下绕弹簧铰支座旋转,车辆安全通过。车辆仅在前部撞击处有少量变形,限高架横梁和立柱均没有明显的屈曲变形。
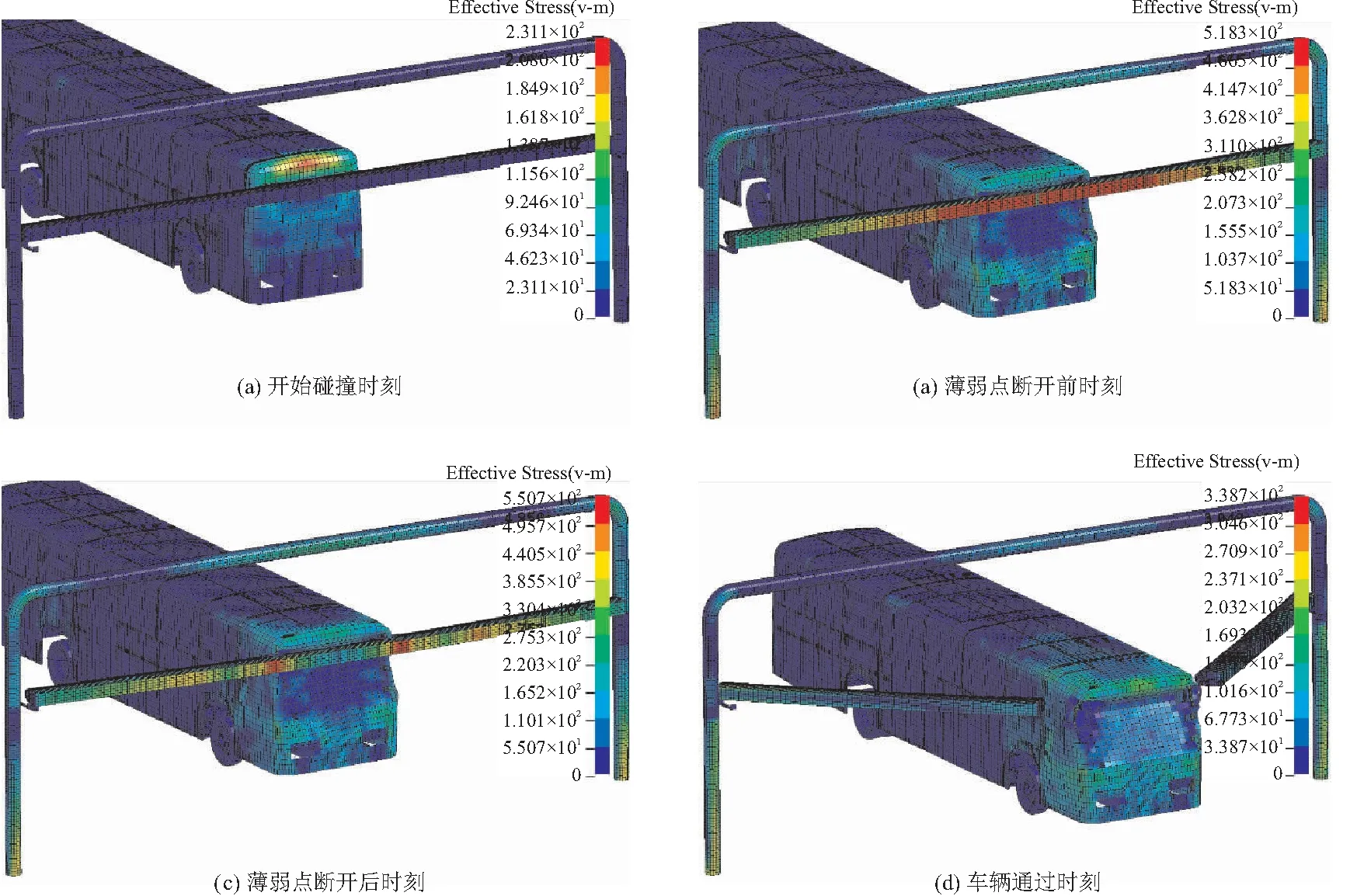
图14 薄弱点断开的柔性限高架应力云图
提取限高架横梁跨中挠度和柱顶位移曲线,如图15所示。为方便与刚性限高架对比,此处的柱顶是与刚性限高架等高位置。刚性限高架的最大横梁跨中挠度为0.755 m,最大柱顶位移为1.202 m。柔性限高架的柱顶位移从薄弱点断开后开始恢复,最大位移仅0.527 m,相比刚性限高架减少了56%。柱顶位移在薄弱点断开时刻后,开始恢复位移并进入振动状态,由于结构阻尼的影响,振动周期逐渐增大,振幅逐渐减小,最终停止。横梁的跨中挠度取横梁断开前的数据,最大跨中挠度仅0.401 m,相比刚性限高架减少47%。
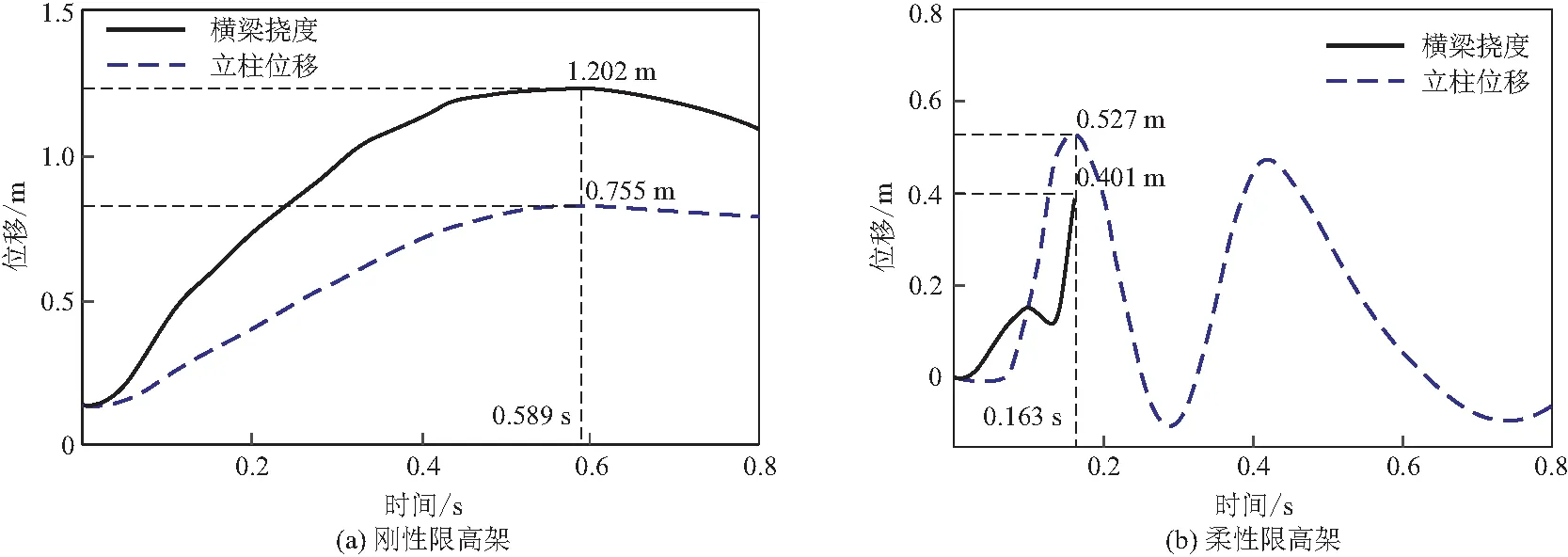
图15 限高架横梁跨中挠度和柱顶位移时程曲线
5.2 车辆变形分析
车辆的切削深度如图16所示。薄弱点断开的柔性限高架工况中,车辆前围框架的弹性变形恢复导致切削深度曲线出现2次波峰,最大切削深度仅0.142 m,相比于刚性限高架工况减少了89%。
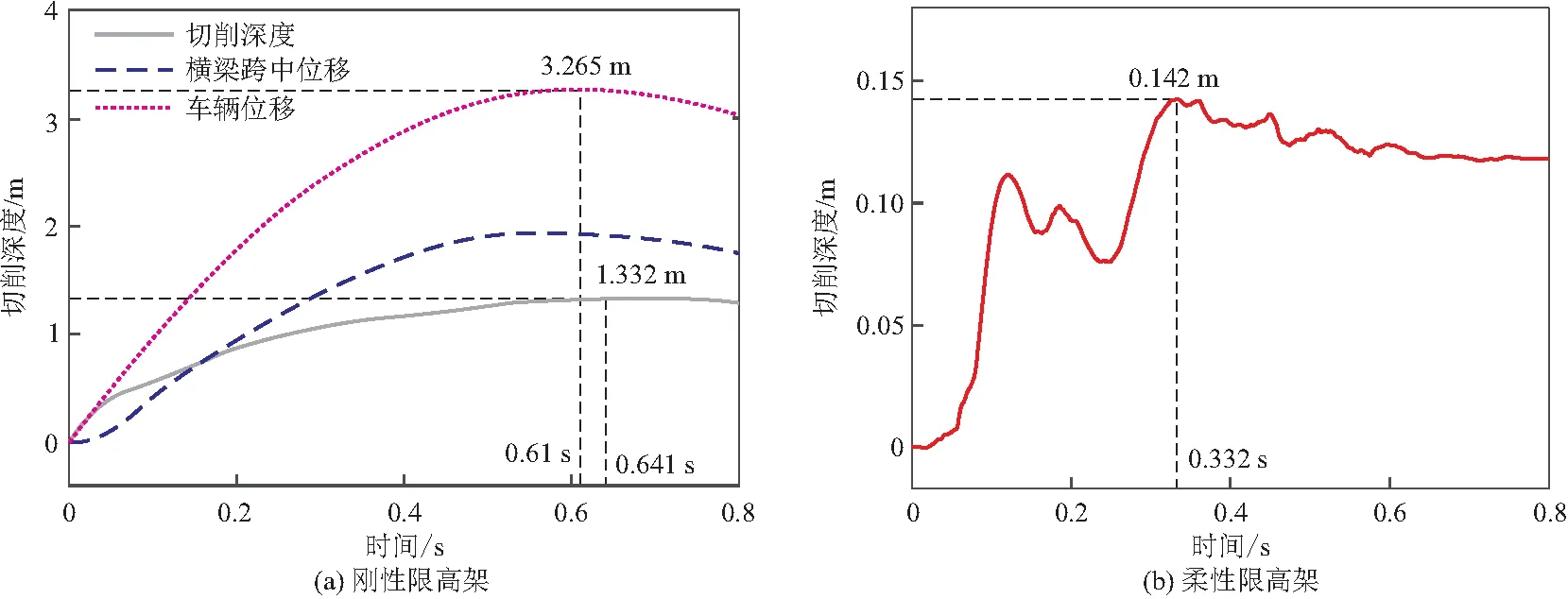
图16 车辆切削深度时程曲线
6 车辆加速度分析
车辆的动能变化较大,速度、加速度是评价车辆损伤的重要指标。车辆碰撞的原始加速度曲线波动较大,无法直观反映对乘员的损害程度,因此,需要对加速度曲线进行简化,提取主要特征参数。
本文选择等效尖顶方波[13,14](Tipped Equivalent Square Wave,TESW)对原有加速度进行简化,此波形的特征是速度变为0时与原波形相同,最大动态变形量与实际车辆的碰撞变形量相等。
选取车辆第一排座椅底部的位移、速度、加速度时程曲线。位移时程曲线整体比较光滑,但是撞击导致位移的微小波动经过二次微分后会被放大,得到的加速度曲线波动较大,难以分析加速度对乘员的伤害影响。
首先计算刚性限高架的等效尖顶方波。 除去车辆与限高架碰撞前的行程时间,得到以撞击时刻为时间起点的原始动力响应曲线,如图17a所示。为验证等效尖顶方波的准确性,对得到的等效尖顶方波分别进行一次积分和二次积分,计算得到对应的等效速度和等效位移时程曲线,并与原始速度和位移曲线对比,如图17b,17c所示。可以看出等效尖顶方波一次积分得到的等效速度时程曲线与原始曲线仅在原始曲线波动较大阶段有少量误差,其他阶段基本重合,而且速度降为0的时刻相同。用等效尖顶方波二次积分得到的等效位移时程曲线与原始曲线基本重合,而且最大位移相等,达到最大位移的时刻相同,满足假设条件。因此,可以认为根据原始加速度曲线拟合的等效尖顶方波效果较好。

图17 刚性限高架工况中车辆的动力响应曲线
按照上述方法计算车辆与薄弱点不断开的柔性限高架撞击时的加速度等效尖顶方波,如图18所示,从图中可以看出等效波形拟合较好。
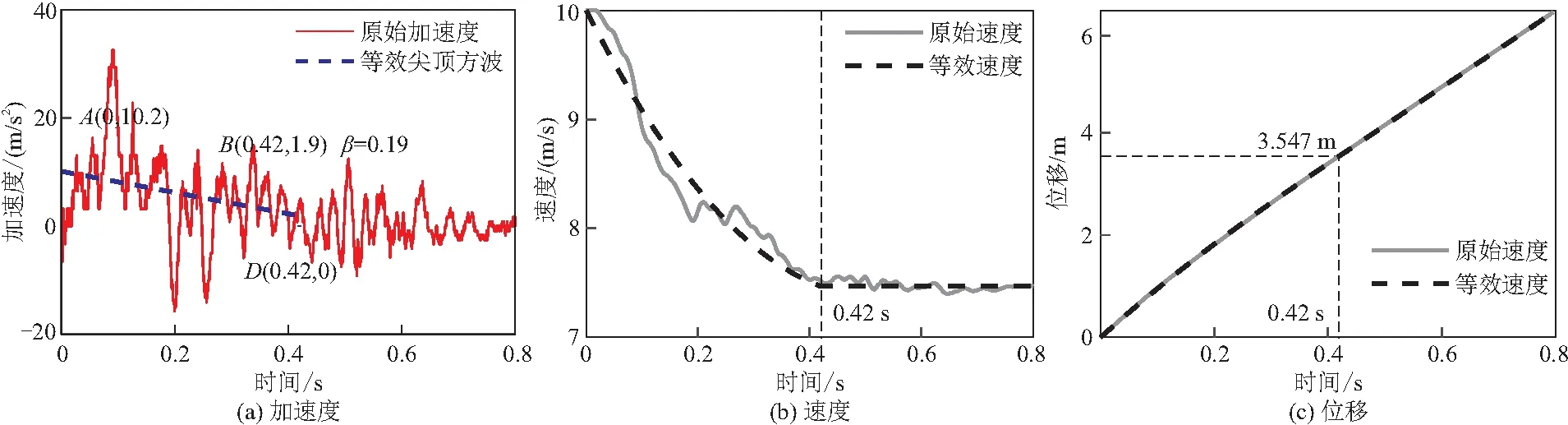
图18 柔性限高架工况中车辆的动力响应曲线
车辆加速度的等效尖顶方波可以分为上升型、平稳型、下降型,其中下降型波形的加速度对乘员的损伤更小,上升型波形的斜率、峰值加速度、加速度放大因子一般与乘员的损伤成正相关[13,15]。
上述两种工况的车辆加速度等效尖顶方波如图19所示。车辆与刚性限高架撞击过程中,加速度上升阶段的斜率为11.70,峰值加速度为20.0 m/s2,加速度放大因子为1.56。车辆与柔性限高架碰撞过程中,车辆在0.42 s后速度基本稳定在7.4 m/s,车辆速度减少26%,加速度的等效尖顶方波变为下降型。综上所述,柔性限高架能明显改善车辆加速度波形,减少乘员损伤。
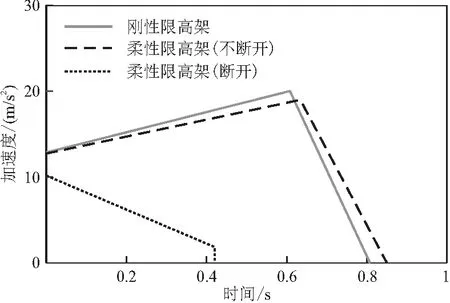
图19 不同工况限高架的等效尖顶方波
7 总 结
本文提出新型柔性限高架的设计理念和结构选型方法,建立精细化的柔性限高架有限元模型进行碰撞分析,从能量、变形、加速度三方面与刚性限高架分析结果对比,得到以下结论:
(1) 薄弱点处4号螺栓为控制螺栓,螺栓轴力在车辆与限高架开始撞击后达到第一峰值,弹簧铰支座达到极限行程后达到第二峰值,也是最大峰值,此时处于撞击力上升阶段,因此以第二峰值为螺栓破坏轴力。
(2) 缓冲橡胶块能明显减小瞬时撞击冲量对限高架横梁的局部破坏,缓冲橡胶块对横梁的受压区有增强作用,使横梁在撞击过程中的挠度和局部变形大大减小。
(3)弹簧铰支座增加横梁变形能力,碰撞过程中车辆动能转化为横梁动能和弹簧势能,薄弱点断开使车辆保留部分速度通过限高架,车辆动能减少34.6%的情况下,内能相比刚性限高架工况减少了64.3%。
(4)柔性限高架的撞击过程中,车辆加速度由最初的上升型波形转换为下降型波形,对驾乘人员伤害更小。

