基于点荷载试验的新生代红砂岩弹性模量估计及其衰变规律研究

陈冠琪， 郭昭赢， 张晓温， 李 剑， 周 哲， 陈佳鑫,4

(1. 中铁十一局集团有限公司第二工程公司， 湖北 十堰 442000； 2. 中铁第四勘察设计院集团有限公司，湖北 武汉 430063； 3. 中国科学院武汉岩土力学研究所， 湖北 武汉 430071；4. 常州大学 环境科学与工程学院， 江苏 常州 213164)

新生代红砂岩是一种含可溶性盐较多的、典型的内陆湖相沉积，主要分布在湖泊退化地区的地表，由于成岩时间晚，岩石胶结性差，使其具有一些独特的工程地质特性[1～3]。新生代红砂岩遇水后易发生软化、崩解，岩层中泥化夹层和层间软弱面较发育，导致岩体强度低、抵抗变形的能力弱。因此，对新生代红砂岩力学特征的影响研究多从裂隙和水这两个关键因素开展。例如，文献[4～6]开展了不同裂隙条件下红砂岩强度特征以及裂隙发育规律；文献[7～9]研究了红砂岩渗透规律、孔隙水压力以及干湿循环对红砂岩力学特征的影响。

岩体力学特征是影响岩土工程安全的首要因素。弹性模量是岩体力学特征的关键参数之一，它反映了岩体承载变形特征。一般情况下，岩石的弹性模量通过单轴或三轴抗压试验得到，但是这种方法操作较为困难，不仅需要取完整的原状样，还需要进行操作复杂的试验，对快速测定岩石弹性模量并不友好。因此，学者们尝试了其他快速测试岩石弹性模量的方法。如丁鹏程[10]建立了现场声波测试数据与岩石弹性模量之间的预测关系。田家勇、高金雪[11，12]基于岩石的声弹理论，通过脉冲回波方法测量双轴加载条件下沿薄板岩样厚度方向传播的超声纵、横波波速变化，来测定岩石的三阶弹性模量。杨凤英[13]利用岩石的储层特性与地震响应之间的关系，建立了基于岩石物理特征的弹性模量测算方法。

以上尝试为岩石弹性模量的快速测定提供了新的思路和借鉴，为了进一步探讨快速测定新生代红砂岩弹性模量的方法，本文利用已开展的新生代红砂岩点荷载试验数据，研究并提出了一种基于点荷载试验的新生代红砂岩弹性模量估计方法，并针对新生代红砂岩遇水软化的特点，研究了其弹性模量的衰变规律，可为相关工程提供借鉴和参考。

1 新生代红砂岩工程性质

1.1 基本物理性质

本次试验所采用的新生代红砂岩取自安徽九华山机场附近，是一种典型的内陆湖相沉积岩。岩石颜色为朱红色，具有很强的风化、崩解及吸水软化特征。新生代红砂岩岩样如图1所示。

图1 新生代红砂岩岩样

通过室内试验，首先确定了天然状态下新生代红砂岩的基本物理性质。具体岩样指标见表1。

表1 新生代红砂岩基本物理指标

1.2 岩样矿物成分与微观结构

通过X衍射试验和电镜扫描试验，对新生代红砂岩的矿物成分和微观结构进行了检测。

图2为新生代红砂岩的矿物成分组成。可以看出，新生代红砂岩中矿物成分含量从高到低依次是石英、蒙脱石、方解石、伊利石和高岭土。由于岩样中含大量蒙脱石，导致新生代红砂岩吸水性较强，且蒙脱石的密度较低，具有很强的吸水膨胀性，故吸水后的蒙脱石体积增大，降低了岩体密度，从而降低了岩体强度。

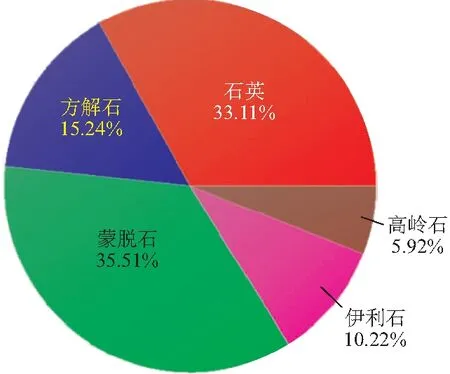
图2 新生代红砂岩矿物组成

图3为新生代红砂岩岩样电镜扫描结果。图中可以看到新生代红砂岩的矿物晶体形态呈蜂窝状，棉絮状，表面附有球形、姜状等形态的颗粒，矿物结构中有明显的空洞和孔隙，容易导水，孔隙度较大。

图3 新生代红砂岩微观结构

1.3 崩解特性试验

图4 为新生代红砂岩在自然环境中进行淋湿 - 风干试验结果，反复干湿循环次数为8次。

图4 新生代红砂岩崩解性试验

可以看出，对于完整红砂岩试样，在干湿循环2～3次后，试样开始缓慢崩解，有碎屑逐渐剥落，试样整体保持一定的完整性，试样主体质量略有降低；在干湿循环4～5次后，试样崩解加速，呈块状、碎屑状剥离，试样完整性降低，但仍可见较大块完整试样，试样主体质量持续减小；在干湿循环6～8次后，试样崩解迅速至崩解完全，完整试样崩解为碎块状、碎屑状以及泥状，难以辨别初始形态，未保留较为完整的试样主体。

1.4 新生代红砂岩单轴抗压强度

针对本次所取的新生代红砂岩开展了单轴抗压强度试验。试验结果如表2所示。

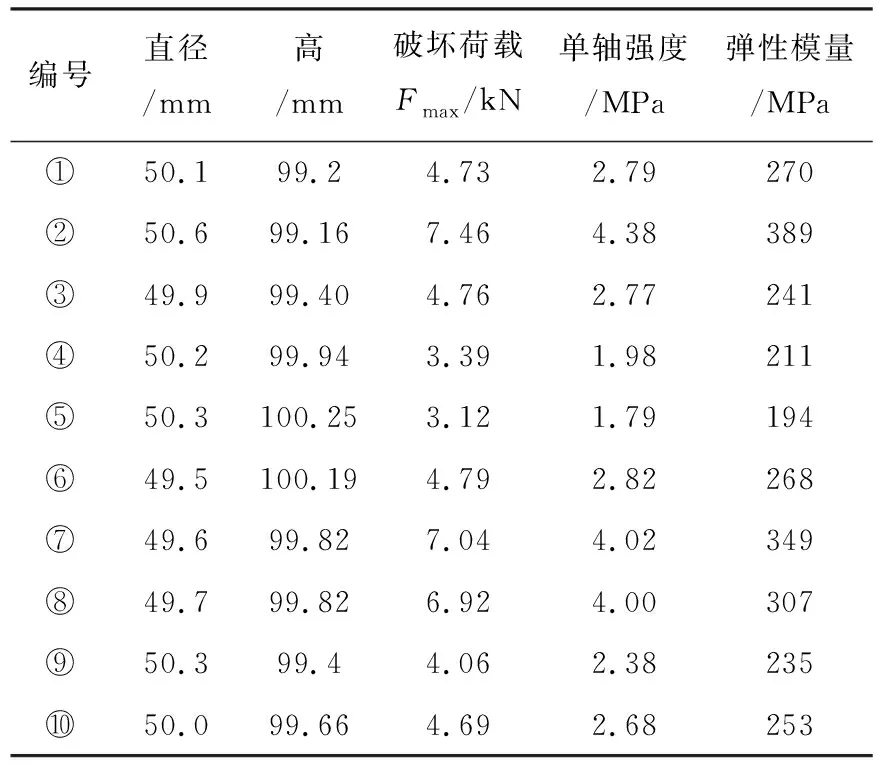
表2 红砂岩单轴抗压强度

可以看到，新生代红砂岩试样最大单轴抗压强度为4.38 MPa，平均抗压强度为2.96 MPa，强度较低，属于软岩类。

1.5 新生代红砂岩工程地质特征

由新生代红砂岩的基本性质、矿物成分及微观结构、崩解特性，并结合成岩方式和时间，可知：

(1)新生代红砂岩由于成岩时间晚，岩石胶结差，有的为半胶结状态，胶结物大都为泥质成分，矿物稳定性差，从而使其具有一些独特的工程地质特性。

(2)新生代红砂岩强度低，遇水后易发生软化、崩解，发育泥化夹层和层间软弱面。经开挖、爆破揭露后，新鲜岩石在自然环境下即可崩解碎裂成土状，甚至泥化。

2 基于点荷载试验的新生代红砂岩弹性模量估计

2.1 新生代红砂岩点荷载试验结果

图5为典型的天然状态下红砂岩的点荷载试验曲线。

图5 新生代红砂岩典型点荷载试验曲线

利用国际岩石力学学会[14]推荐的方法，对天然状态下新生代红砂岩点荷载试验结果进行处理。其中修正后的点荷载强度与换算的单轴抗压强度之间的倍数关系取8.96[15]，具体结果见表3。

表3 基于点荷载换算的单轴抗压强度

2.2 新生代红砂岩弹性模量

根据前述开展的新生代红砂岩单轴抗压强度试验，计算得到了其弹性模量，如表2所示。

通过10组试样试验结果的对比，可以看到，对于新生代红砂岩来讲，其弹性模量与单轴抗压强度有较强的对应关系，不同试样的弹性模量与单轴抗压强度的比值在87～108之间，平均94左右。

2.3 基于点荷载试验的弹性模量估计方法

从新生代红砂岩点荷载试验曲线上看，除了在加载端与岩样初始接触的瞬间有一段微小的平缓曲线，试验过程中岩样的荷载 - 位移曲线基本处于直线发展，因此，可以认为点荷载试验状态下，新生代红砂岩的表征弹性模量可以用点荷载强度换算后的单轴抗压强度与点荷载应变的比值来确定。此处定义点荷载应变为岩样破坏时加载端位移与等效直径的比值。

以点荷载试验为基础的表征弹性模量可以用下式表示：

(1)

式中：Edzh为点荷载表征弹性模量；σdzh为点荷载换算的单轴抗压强度；εdzh为点荷载应变，可用式(2)计算。

(2)

式中:db为岩样破坏时，加载端的位移；De为等效直径[11]。

利用上述公式对点荷载试验数据进行处理后，新生代红砂岩的表征弹性模量数据，以及利用单轴抗压强度与弹性模量的关系计算得到的弹性模量数据均如表4所示。

表4 基于点荷载换算的弹性模量

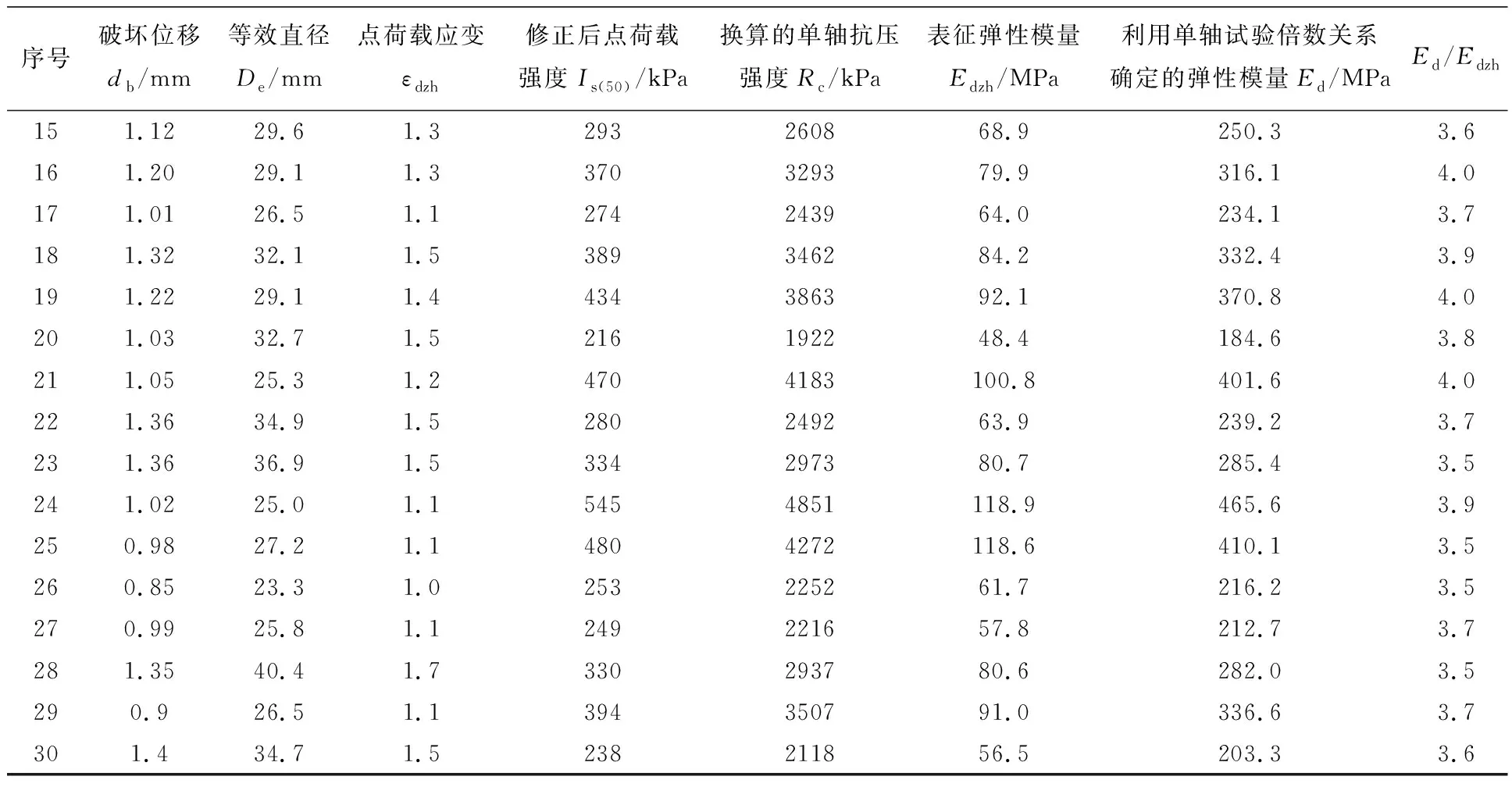
续表4

从新生代红砂岩表征弹性模量与单轴强度确定的弹性模量之间的关系来看，二者的倍数关系在3.5～4.0倍之间，表明基于点荷载试验的表征弹性模量与新生代红砂岩弹性模量之间有较好的比值关系，基于点荷载试验的红砂岩弹性模量的估计方法可以用式(3)表示。图6为新生代红砂岩弹性模量Ed与表征弹性模量Edzh之间的对应关系。图中可以看到，二者之间有较好的对应关系，相关系数达到0.96以上。实际应用时，建议红砂岩弹性模量与表征弹性模量之间的倍数关系k取3.7。

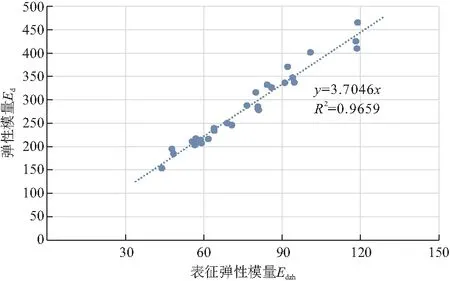
图6 Ed - Edzh关系曲线

E=kEdzh

(3)

式中：E为新生代红砂岩弹性模量；k为倍数关系比值，根据试验确定。

需要指出的是，利用式(3)得到的红砂岩弹性模量准确与否，与基于点荷载试验的表征弹性模量直接相关。而表征弹性模量的计算与点荷载试验数据的精度相关，如等效直径De是否准确等，为保证弹性模量的准确性，开展点荷载试验时需严格遵守国际岩石力学学会推荐的试验方法和步骤。

3 新生代红砂岩弹性模量衰变规律

从新生代红砂岩的基本物理力学试验结果及其工程性质分析可知，新生代红砂岩具有很强的风化和崩解性，对水的敏感性很高，因此，在吸水软化的情况下，其弹性模量也必然出现迅速衰减的情况。

如图7不同含水率下新生代红砂岩点荷载试验曲线所示，不同含水量下，新生代红砂岩的位移 - 荷载曲线峰值逐渐向右移动，荷载峰值也不断减小，说明随着含水量的增加，新生代红砂岩的强度不断降低，其弹性模量也不断衰减。

图7 不同含水率下新生代红砂岩点荷载试验曲线

图8为不同含水率状态下，新生代红砂岩弹性模量衰减曲线。

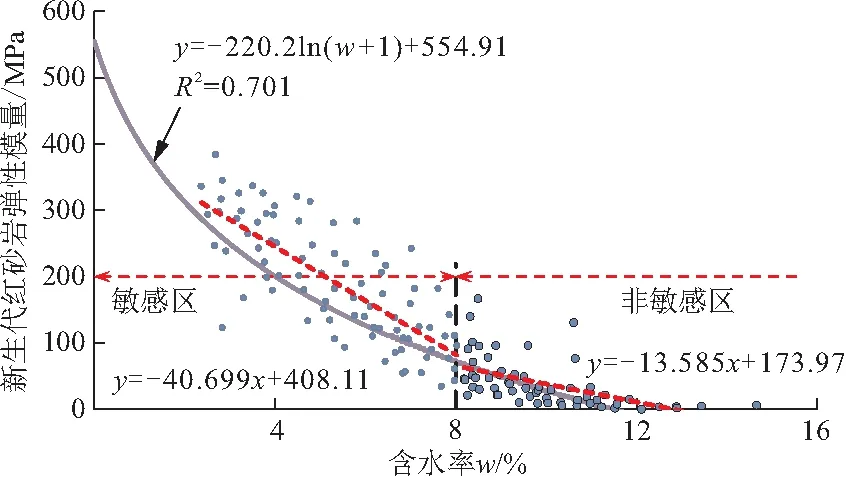
图8 新生代红砂岩弹性模量衰减曲线

从图8可以看到，随着含水率的增加，新生代红砂岩的弹性模量呈明显的衰减趋势，说明水对新生代红砂岩弹性模量的影响极大。

为了进一步描述新生代红砂岩弹性模量与含水率之间的关系，采用负指数函数对其进行拟合，得到新生代红砂岩弹性模量衰减曲线。

E=554.9-220.3ln(w+1)

(4)

此外，从图7中还可以看到，当新生代红砂岩含水率小于8%时，其弹性模量衰减迅速，当含水率超过8%时，弹性模量的衰减速度降低，说明新生代红砂岩的初始含水率对其弹性模量的衰减有重要影响，当初始含水率较低时，其弹性模量随含水率的增加而衰减迅速，当初始含水率较高时，其含水率的变化对其弹性模量影响较小。

4 结 论

本文通过对新生代红砂岩基本物理特性的研究，掌握了新生代红砂岩的工程地质特征，在此基础上，通过点荷载试验曲线，提出了基于点荷载试验的新生代红砂岩弹性模量的估计方法，并研究了新生代红砂岩弹性模量衰减规律，主要结论如下：

(1)以单轴抗压试验得到的弹性模量为基础，基于点荷载试验数据，提出新生代红砂岩点荷载试验表征弹性模量与实际弹性模量之间的换算关系，建立了基于点荷载试验的新生代红砂岩弹性模量估算方法。

(2)研究了新生代红砂岩不同含水率条件下弹性模量的衰减规律，提出了新生代红砂岩弹性模量随含水率增加而衰减的经验公式，为相关工程提供了参考依据。

(3)研究得到了影响新生代红砂岩弹性模量衰减的临界含水率，即8%。当初始含水率小于8%时，新生代红砂岩弹性模量随含水率的增加而衰减明显，当初始含水率大于8%时，其弹性模量衰减不甚明显。