面向流场性能提升的地铁送风风道拓扑优化研究

曹月昊 ，孙峪鹏 ，尉洋，黄羽鹏，周亿莉，姚松

(1.中南大学 交通运输工程学院，轨道交通安全教育部重点实验室，湖南 长沙，410075；2.中南大学 轨道交通安全关键技术国际合作联合实验室，湖南 长沙，410075；3.中南大学 轨道交通列车安全保障技术国家地方联合工程研究中心，湖南 长沙，410075)

在城市公共交通体系中，地铁因具有安全环保、运量大等特点成为了主流的交通出行方式。新形势要求地铁各系统应满足人性化设计，乘客舒适性已经成为地铁车辆性能评估的主要指标之一。在地铁各系统中，地铁空调通风系统调节列车内外空气，且送风风道作为其重要部件，负责引导气流流向，控制送风出口送风状态，影响着乘客的整体舒适度。地铁在运营过程中常出现送风量不均匀、风向直吹、冷热变化过大等问题，为合理组织车厢内气流分布，控制车内的微风速，许多学者对地铁送风风道结构进行优化，以改善风道送风的均匀性。

王斌[1]通过流场仿真观察到靠近空调机组的送风风道出口存在回流现象，基于经验在送风风道进口两侧增加穿孔挡板使得此现象得到缓解。刘家林等[2]采取在送风风道内部增加相应隔板、封堵一些送风口、加装导流管等内部扰流措施，使得风道送风更为均匀。尤立伟等[3]利用不均匀系数对风道内的气流组织进行评价，并通过调整孔板参数对非变截面风道进行结构优化。胡滋艳[4]研究了地铁送风风道出口导流板的送风角度对温度场、速度场、流场涡结构及PMV-PPD 评价指标的影响，通过参数优化得到了最优的送风角度。KIM等[5]利用2k因子设计方法对顶风风道系统的设计参数进行有效性评价(其中，k为影响因素数量，2表示影响因素的两个方面)，并采用响应面法设计了具有改善流动均匀性的优化模型，有效地抑制初始模型中存在的非均匀流分量。夏春晶等[6]在分析风道通风性能的基础上对风道主体、送风孔缝、送风格栅等结构进行优化，有效地改善了送风均匀性。

以上地铁送风风道结构优化方法的核心是借助CFD 技术，依据经验在送风风道中增添构型简单的导流结构，并采用尺寸优化方法[7]寻求此初始构型限制下的局部最优解。此类方法的优化潜力严重依赖于导流结构的初始构型，优化设计的理念局限于原有结构的改进，无法实现最优的效果。本文则将拓扑优化方法应用于地铁车厢送风风道结构优化中，以风道出口处气流均匀性偏差最小化与进出口平均压差最小化为目标，从拓扑构型寻求当前边界条件下固体与流体区域的最优分布，优化设计具有良好流场性能的新型导流结构，送风风道出口处速度均匀性与进出口平均压差都明显降低。

1 初始送风风道流场性能分析

1.1 几何模型

现有地铁送风风道分布在车厢顶部，且每节车厢布置2 个空调机与2 组送风风道。2 组送风风道相对车厢中心呈对称分布，分别控制车厢横向两侧送风状态。提取单侧送风风道作为流场分析的研究对象，并在简化模型的过程中保留出口导流板、风道固定内筋等关键结构。图1所示该地铁送风风道的初始结构，风道内腔高为0.29 m，风道进口宽为0.85 m，风道出口较为狭长，长为11.44 m，且部分出口区域靠近进风口，部分出口区域靠近风道尾部尖端。

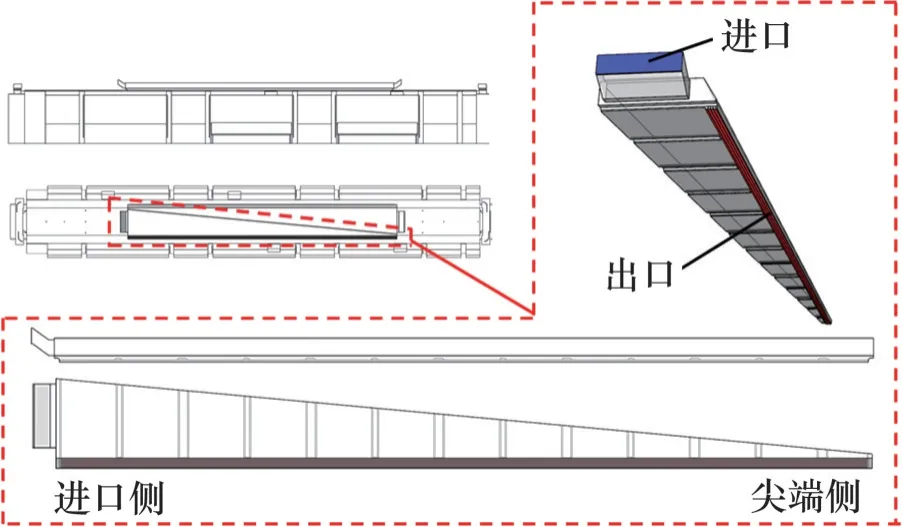
图1 地铁车厢送风风道的布局与结构Fig.1 Layout and structure of air supply duct for subway cars

1.2 物性参数与边界条件

此送风风道标准送风量为4 300 m3/h，内部空气密度取1.225 kg/m3，动力黏度取1.86×10-5kg/(m·s)。风道进口设为速度进口边界条件，进口速度根据标准参数换算为6.862 8 m/s；风道出口设为压力出口边界条件；风道壁面设为无滑移壁面边界条件。

1.3 计算网格与湍流模型

以六面体网格为主对网格进行划分，网格的基础边长设为0.02 m，并在风道壁面添加3层边界层，总体网格数约为80 万个。具体网格如图2所示。

图2 风道网格划分Fig.2 Grid division of air duct

地铁送风风道内流动为湍流流动，且马赫数低于0.3，流体的密度变化很小，故采用定常、黏性、不可压缩N-S方程与标准k-ε湍流模型[8]进行仿真模拟。

1.4 结果分析

图3(a)所示为送风风道出口表面的速度分布情况。由于风道出口构型较狭长，且进口处额定流速较快，出口表面处的速度分布产生了明显的分层，靠近进口侧的出口区域速度较小，而远离进口侧的出口尖端区域则产生了较大的速度，部分区域的速度达6 m/s。图3(b)所示为风道出口表面法向速度矢量的分布情况。靠近进口侧的出口区域产生了回流现象，而远离进口侧的出口尖端区域则出现了法向风速过高情况。

图3 风道出口的速度分布情况Fig.3 Velocity distribution at the outlet of air duct

影响送风风道流场性能的主要因素为送风均匀性与进出口压差，而工程上需在一定进出口压差限制下尽可能提高出口均匀性，以保证客室内气流分布的合理性。送风均匀性评价指标为速度均匀性系数γm(速度完全均匀时，γm=1)，进出口压差定义为进出口压强之差Δp，其计算公式分别为：

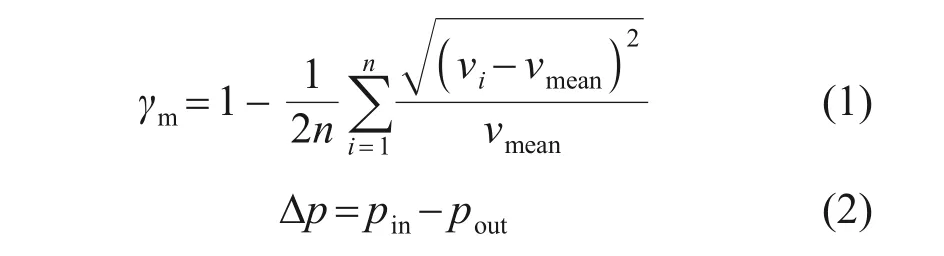
其中：n为出口平面网格个数；vi为每个网格处的平均风速；vmean为整个出口处的平均风速；pin为进口处平均压强；pout为出口处平均压强。为评估送风风道出口的送风均匀性，分别将出口表面速度以及法向速度矢量代入式(1)，以求得送风风道出口速度均匀性系数γt与法向速度均匀性系数γv。

根据式(1)和(2)可求得初始送风风道出口速度均匀性系数γt为0.7912，法向速度均匀性系数γv为0.585 9，进出口压差Δp为23.879 22 Pa。由于送风风道出口具有“横向窄、纵向长”的特性，出口处送风均匀性主要取决于出口处法向速度分布，因此，减少出口近端的回流现象与远处尖端的风速过高情况是亟待解决的问题。

2 拓扑优化理论

2.1 拓扑优化问题设计

拓扑优化求解的一般形式[9]为：

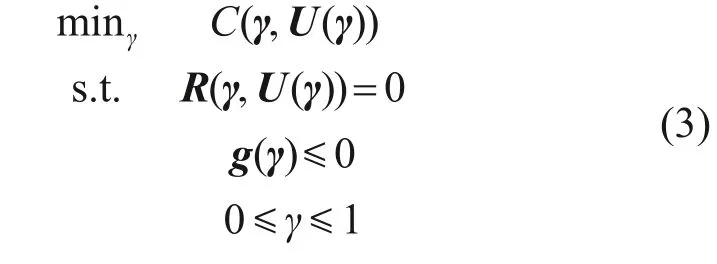
其中：γ为设计变量γ组成的向量，流体拓扑优化中γ定义为材料的渗透能力(反渗透的固体材料单元γ为0，流体单元γ为1，中间单元则考虑为不同孔隙率的多孔介质材料)；C为优化问题的目标函数；R为优化问题的控制方程；U为随γ变化的状态变量；g为优化问题的约束方程。

2.2 适应拓扑优化的修正k-ε模型

固体结构拓扑优化常采用变密度法对弹性模量进行插值[10]，流体拓扑优化则需要在流动控制方程中添加达西插值项[11]，使得γ实现反渗透固体与流体单元之间的相互转化。拓扑优化应用于层流流动，只需要对N-S 方程中的动量模型进行修正[12-15]；而拓扑优化应用于湍流流动，在对标准k-ε模型中动量方程进行修正的同时，还需考虑湍流流动中拓扑变形引起的湍流能量变化，将类似的插值项加入k与ε的传输方程[16]中，使得固体区域边界速度、湍流动能以及湍流耗散能均设定为0。

修正后的不可压缩流标准k-ε模型为：

在惩罚项中，λ为布林克曼惩罚系数(将优化过程中产生的多孔介质单元推向反渗透固体或流体单元，取1 000)；α(γ)函数为实现固体与流体空间变化的插值函数；q为达西罚函数系数(控制插值函数的曲率，取0.1)。

2.3 拓扑优化算法流程

为实现拓扑分布不断向更优构型迭代，且考虑到求解复杂度问题，采用伴随法[17]对优化问题的灵敏度进行计算，选择移动渐近线方法[18]求解优化模型，同时采用亥姆霍兹方程[19]对材料体积因子进行过滤，并将过滤的结果通过双曲正切投影[20]进行处理以获得清晰的拓扑边界。整个拓扑优化算法流程如图4所示。

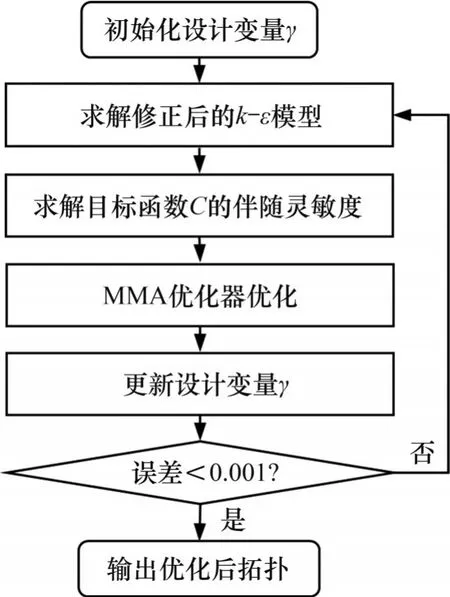
图4 拓扑优化流程Fig.4 Flow of turbulent topology optimization

3 送风风道结构拓扑优化设计

在上述流场分析中，风道出口处气流速度差异主要在于风道结构的变截面设计。考虑到三维湍流有限元计算与伴随灵敏度求解所需时间较长，为提高优化效率，将优化区域简化为风道的水平横截面，保留初始风道的变截面特性，采用二维简化模型对风道进行拓扑优化设计。与三维初始风道的边界条件相同，二维风道进口风速为6.862 8 m/s。

在本次优化设计中，二维流道出口区域被划分为50 个等长区域(即n=50)，设每个小出口的平均速度为vj，整个出口平均速度为vmean，进口处平均压强为pin，出口处平均压强为pout。优化的目标是尽可能减小风道出口均匀性偏差，同时避免风道进出口压差过大。优化中无约束，目标函数C包括出口均匀性偏差与进出口平均压差两部分[21]，其中出口均匀性偏差为1-γm，进出口平均压差为Δp。计算当前区域下1-γm与Δp的初始值，结合均匀性目标在风道优化中的重要性，且考虑到压差目标的作用是在实现均匀性目标过程中避免风道阻力急剧增加，经过反复试算后，最终调节目标函数中权重因子ω1与ω2分别为400 和1。整体目标函数公式为

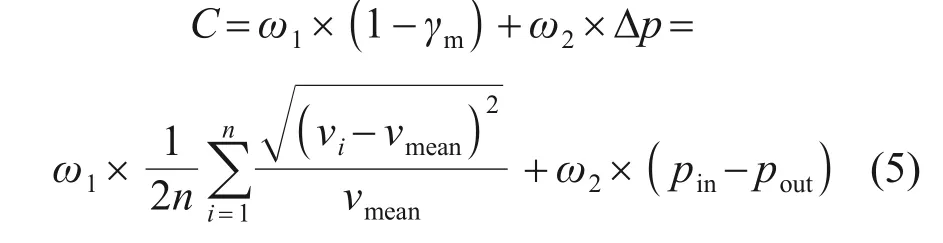
由于流体拓扑优化中存在流体与固体的转化关系，为防止优化进程中进口或出口处出现固体阻塞从而影响优化迭代，将二维风道主体内腔作为设计区域，进口区域与出口区域作为非设计区域，优化的初始设计布局如图5所示。

图5 风道优化问题的设计模型Fig.5 Design model of air duct optimization problem

4 送风风道优化结果分析

4.1 优化结果

计算使用高性能工作站(2 个E5-2650 v4 处理器，24 核，128 G 内存)，历时约4 h，迭代每步耗时约140 s。伴随着优化进程，在二维设计域腔内逐渐生成边界较为清晰的固体区域，约经过100次迭代后目标函数收敛。优化进程如图6所示。

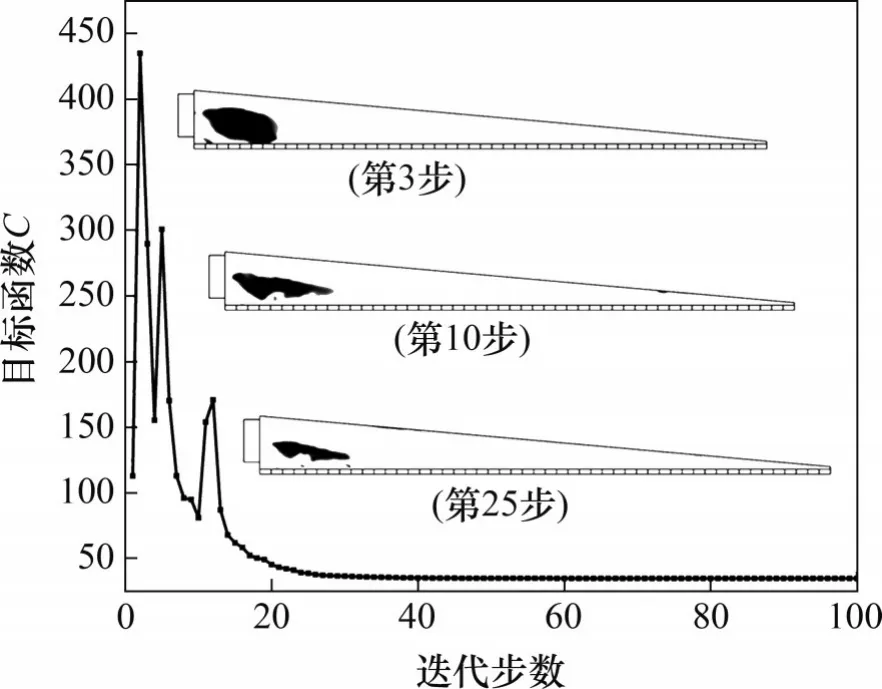
图6 优化进程Fig.6 Optimization processes

优化得到的构型在边缘处仍然存在少许中间渗透率单元，为得到清晰的几何边界，选取γ≤0.5的区域作为固体域，γ＞0.5作为流体域，最终得到的拓扑构型如图7所示。

图7 优化后拓扑构型Fig.7 Layout of the optimized topology

结合上述二维设计空间的优化结果，提取优化所得的二维固体域，拉伸0.29 m 得到三维拓扑导流结构，使其高度与初始风道内腔高度相同，并将此固体域赋予到初始风道内腔的相应位置上，重建后可得新型三维送风风道模型。新型送风风道结构如图8所示。

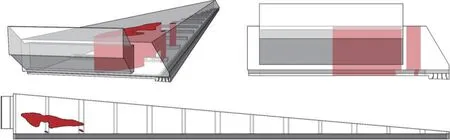
图8 新型送风风道结构Fig.8 Three-dimensional mapping model of the optimized configuration

4.2 优化后风道出口速度分布

为验证新型三维送风风道内流场性能，将重建后的三维送风风道模型进行仿真分析，其物性参数、进出口边界条件与初始风道的物性参数保持一致，内部拓扑导流结构与风道外壁设置为非滑移壁面条件。数值模拟收敛后得到风道出口处速度分布情况以及法向速度矢量分布情况，如图9所示。

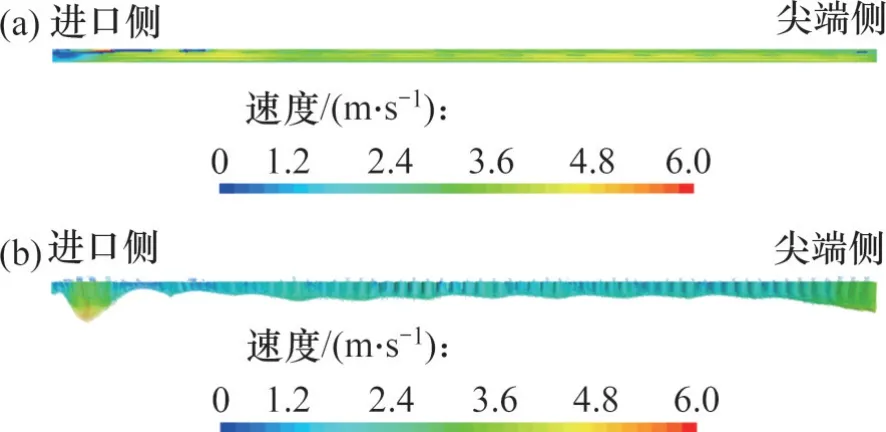
图9 优化后风道出口的速度分布情况Fig.9 Velocity distribution at the outlet of the optimized air duct

风道出口处的速度分布较优化前有明显改善，进口侧出口处的低风速区域变小，尖端侧出口处的高风速区域消失。从出口处法向速度矢量分布可知，进口侧的出口区域风速有所增加，且回流现象基本消除；尖端侧的出口区域风速过高情况减弱，风速分布更均匀。

根据式(1)与(2)，优化后的送风风道出口速度均匀性系数γt为0.889 5，法向速度均匀性系数为0.785 4，进出口平均压差为20.909 1 Pa。优化后的风道送风性能提升显著，两项均匀性系数分别增加12%和34%，同时，进出口压差减小12%，优化前后对比如表1所示。

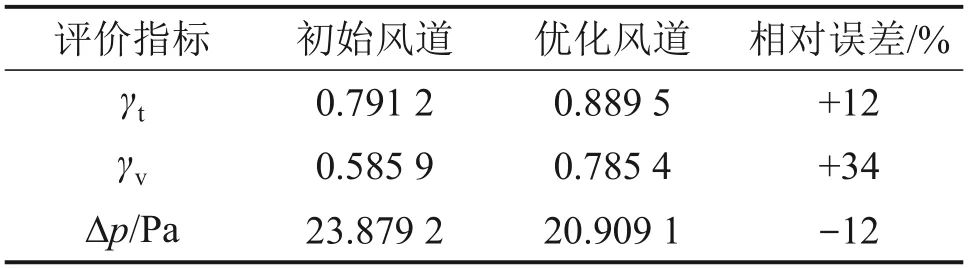
表1 初始风道与优化后风道送风性能对比Table 1 Comparison of the air supply performance between the initial air duct and the optimized air duct

4.3 拓扑结果评价

经过优化后所得的新型送风风道并没有改变几何外形，继续沿用初始送风风道的外部构型，只是将拓扑优化所得的导流结构添加到风道内腔中。此导流结构外形并不规则，相对传统的导流板制造更复杂，但其使得送风风道的流场性能大幅度提升，在提高风道送风均匀性的同时，降低了进出口平均压差，对于地铁送风风道优化设计具有较好的参考价值。

5 结论

1) 地铁送风风道出口较为狭长，在额定送风条件下，初始送风风道在进口侧处的出口区域存在回流现象，在尾部尖端的出口区域存在风速过高情况。

2) 本文将变密度拓扑优化理论应用于湍流流场中，在k-ε湍流模型的动量方程、湍流动能方程以及湍流耗散率方程中添加类似的达西插值项来实现反渗流固体与流体单元的相互转化，并采用伴随灵敏度法求解目标梯度，提出了适用于湍流流动的流体拓扑优化方法。

3) 将此拓扑优化方法应用于地铁送风风道的优化设计，目标函数采用多目标函数加权处理的方式，考虑风道出口处气流均匀性偏差与进出口平均压差两部分。优化后的地铁送风风道出口均匀性显著提高，初始风道出口处存在的回流现象、尖端风速过高情况基本消除。风道出口处截面速度均匀性系数增加12%，法向速度均匀性系数增加34%，进出口平均压差减小12%。