融合相似度和预筛选模式的协同过滤算法

赵文涛，田欢欢，冯婷婷，崔自恒

河南理工大学计算机科学与技术学院，河南焦作454000

大数据时代的到来，数据规模明显扩大，导致用户寻找的有效信息和冗余信息的矛盾尖锐，信息过载[1]问题日益严重。推荐系统[2]是一种信息过滤技术，帮助用户快速准确地获取感兴趣的内容，提供个性化推荐。基于邻域的协同过滤[3-4]是一种应用广泛的推荐算法，其中用户（项目）相似度的确定是协同过滤算法的核心步骤[5]，它不仅决定近邻的选择，而且对预测和推荐结果有决定性影响。

传统相似度主要分为数值型相似度、结构型相似度和混合型相似度。数值型相似度如余弦相似度（cosine similarity，COS）[6]、皮尔逊相关系数（Pearson correlation coefficient，PCC）[7]和平均绝对误差（mean absolute difference，MSD）[8]等，仅考虑共同评分项目中评分数值差异，在稀疏数据下相似度计算较不准确。结构型相似度不同于数值型相似度，如杰卡德系数（Jaccard）[9]只考虑共同评分项目数量占比。混合型相似度综合考虑用户评分的数值和结构信息，如JMSD[10]是Jaccard 和MSD 的组合，SPCC[11]结合Sigmoid 函数与PCC，具有更好的推荐质量。但这些方法都依赖共同评分项目，随着用户和项目数量的增加，数据集越来越稀疏，导致推荐准确性降低。许多研究人员致力于从提升预测准确度和推荐质量方面，提出不同的改进算法来缓解数据稀疏[12-13]和冷启动[14-15]问题。其中，新非线性启发式相似度（new heuristic similarity model，NHSM）[16]综合考虑用户评分的局部上下文信息和评分偏好。最近提出基于评分概率分布的相似度，包括BCF（Bhattacharyya coefficient）[17]和KLCF[18]等，计算相似度时使用评分矩阵中所有的评分数据。这些改进方法可在一定程度上缓解数据稀疏和冷启动问题，提高推荐准确性，但时间复杂度和计算成本较高。

基于以上分析，本文提出一种融合相似度和预筛选模式的协同过滤算法，更好地平衡推荐准确性和时间效率的关系。首先提出一种基于用户的相似度，其中定义相对评分差异，并列举相似度应满足的定性条件，结合放大部分相似度值的需求，得到基于exp(-x)函数的相似度公式，同时考虑基于信息熵改进的评分偏好和用户的全局评分数量信息作为权重因子以区分用户间差异，提高稀疏数据中相似度计算的可靠性。其次根据相似度和评分预测公式中的隐式约束，提出预筛选模式。在不影响推荐结果的前提下，过滤掉不参与计算的用户及相应的评分数据，进一步提高计算效率。最终融合相似度和预筛选模式的协同过滤算法，在保持较低时间成本的同时，也具有良好的预测和推荐质量。

1 相关工作

1.1 准确性和效率的权衡

推荐系统的目的是帮助用户以较低的搜索成本[19-20]和更高的推荐准确性[21-23]来获取感兴趣的产品或服务，从而提高用户体验。随着信息资源爆炸式增长，推荐系统面临着数据稀疏、准确性与效率的权衡等重大挑战。

就准确性而言，目前提出的推荐算法[16-18,24-25]主要通过设计复杂的相似度来提高推荐准确性，但往往忽略时间效率。Liu 等人[16]引入非线性启发式相似度NHSM，由接近度、重要性和奇异性（proximity-significance-singularity，PSS）组成，同时考虑共同评分项目的比例（Jaccard）以及用户评分偏好的影响。Patra 等人[17]提出基于巴氏系数的线性相似度BCF，同时考虑共同评分项目占比（Jaccard）。Wang 等人[18]提出非线性KLCF，利用扩展的NHSM 模型并结合KL 散度，综合计算用户相似度。受注意力机制的启发，Fu等人[24]提出一种项目相似度，自适应地捕捉近邻间的关系来进行评分预测，能获得较好的推荐结果。Polatidis等人[25]提出一种动态的多层次协同过滤算法，以提高推荐准确性。

就效率而言，最近提出的算法[26-30]致力于在保持一定推荐准确性的同时降低计算成本。Bag 等人[26]提出相关杰卡德系数（related Jaccard，RJaccard）和相关JMSD（related JMSD，RJMSD）对相关邻域进行分类，在较短的时间内生成推荐。Zhang 等人[27]结合蜂群聚类，提出一种新的协同过滤算法，只需计算类内用户间的相似度，降低近邻搜索范围。Liu 等人[28]提出一种新的潜因子模型（latent collaborative relations，LCR），在保持推荐准确性的同时，为目标用户提供快速的推荐。Chae 等人[29]为基于邻域的相似度分别设计了新的数据结构，有效地识别近邻，提高时间效率。Wang 等人[30]提出一种相似度框架，综合考虑数值和结构型相似度，更高效地产生推荐。

根据以上分析，通过设计更为复杂的相似度可在一定程度上改进预测和推荐质量，但计算复杂度较高，导致时间效率显著降低。为了更好地权衡准确度和时间效率的关系，迫切需要一种简单高效的方法，在保持较低时间成本的同时，也具有良好的预测和推荐质量。

1.2 评分预测公式

协同过滤算法中，除相似度的确定之外，评分预测公式也影响最终预测和推荐结果。通常使用的是基于加权平均的评分预测公式[31]，如式（1）所示。

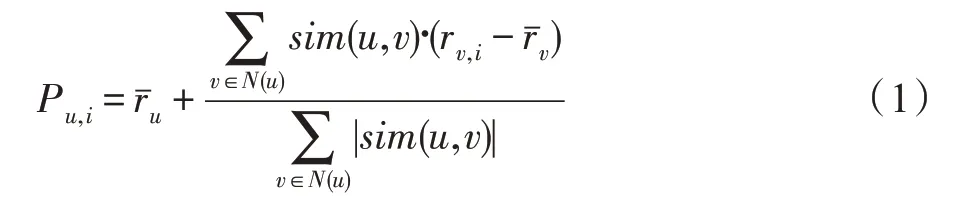
其中，用户u的评分均值为，N(·)为目标用户u的邻居集，近邻对物品i的评分为rv,i，sim(u,v)为用户间相似度。这里假设：如果目标用户u对未评分物品i无法计算或预测时，将直接忽略Pu,i。

2 本文提出的方法

为在较低的时间成本内提供良好的推荐，首先提出一种简单高效的相似度，以缓解稀疏数据下相似度计算的准确性问题。然后根据相似度和评分预测公式中的隐式约束，提出预筛选模式，进一步提高时间效率。

2.1 相似度模型

提出的相似度（score enhanced similarity，SES）表达式共由三部分组成：第一部分是基于相对评分差异优化的相似度，第二部分为基于信息熵改进的用户评分偏好，第三部分考虑用户的全局评分数量信息。拟议的用户相似度最终公式如式（2）所示。

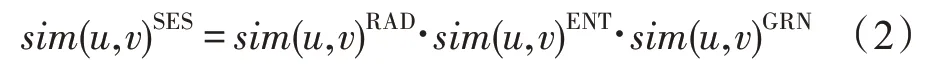
2.1.1 基于相对评分差异优化的相似度

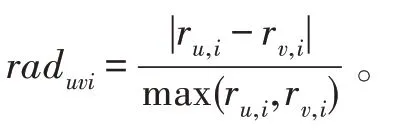
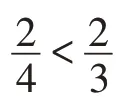
直接使用相对评分差异的原始定义衡量相似度显然不够准确，通常可加入一些相似度应满足的定性条件将其达到优化，即通过对表示函数f(raduvi)的raduvi值进行变换，可得到调整的相似度值。这种变换首先需满足以下条件：（1）f(·)的定义域为[0,1]；（2）f(·)是相似度函数，值域也为[0,1]；（3）f(·)严格连续且单调递减。

除以上相似度应满足的基本条件外，函数f(·)的选择还应当以放大部分相似度值为主要依据。具体表现为：当raduvi的值很小甚至趋近于0 时，用户间的相似度很高并且趋近于1，函数的变化率应越来越快；当raduvi变大甚至趋近于1 时，用户间的相似度很低并且趋近于0，函数的变化率应越来越慢。即需满足raduvi趋于0 时，f(·)的变化率比raduvi趋于1 时更重要，这种变化趋势能更好地区分相似度高的用户间差异，所选的最近邻参与评分预测时结果也更有区分度。综合以上分析，函数exp(-x)不仅满足所有要求的定性条件，而且是形式简单的非线性函数，具有成为相似度的天然优势。最终基于exp(-x)函数衡量相对评分差异的相似度，公式如式（3）所示。

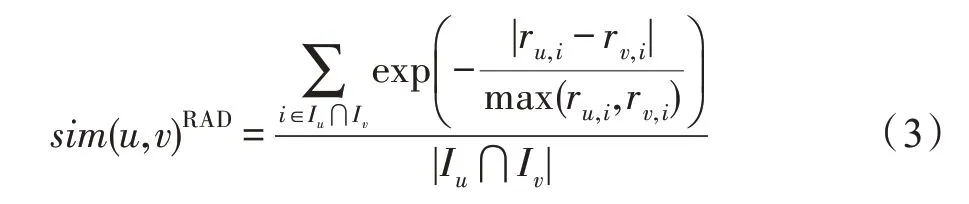
其中，max(ru,i,rv,i)是指ru,i与rv,i中的最大值，Iu表示用户u的评分项目集。

2.1.2 基于信息熵改进的用户评分偏好

对于同样喜爱的物品，不同的用户会根据自己的评分偏好给出不同的评分值，这将降低推荐准确性。受NHSM 中用户评分偏好的启发，提出基于信息熵改进的评分偏好公式，以衡量和区分用户评分偏好对推荐结果的影响。

信息熵可以衡量用户的评分分布以及信息量情况，信息熵越大表示用户的评分分布较均匀且包含的信息量较大，信息熵越小表示用户的评分分布较集中且包含的信息量较小。信息熵的分布范围能够有效体现不同用户的区分度，且根据信息熵的性质，熵值较小的用户表明其行为可信度较低，因此选取信息熵的倒数来调整用户差异度，具体表现为：放大熵值较小的用户差异度，缩小熵值较大的用户差异度，使得引入信息熵的方式更具合理性。最终综合用户均值差和信息熵的倒数差，提出基于信息熵改进的评分偏好公式，如式（4）所示，更好地衡量用户的评分偏好，有效地刻画用户间的差异性，从而提高用户间相似度计算的准确性。

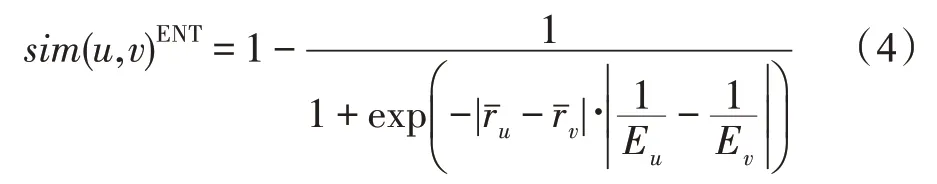
其中，Eu、Ev分别代表用户u和v的信息熵，Eu的计算公式如式（5）所示，其中当前评分值k在用户u的评分向量中所占比例为p(k)，X表示评分值k的取值范围。

2.1.3 用户全局评分的数量信息

传统相似度仅考虑共同评分项目的信息来识别最近邻，然后通过最近邻对同一物品的评分情况进行预测，但有时这个过程并不适合预测未评分物品的评分值。假设两个用户非常相似，但只对共同评分项目有评分，这种情况下相似的用户对各自的评分预测没有贡献。因此非共同评分项目的信息对产生评分预测有重要影响。

针对这一问题提出基于用户全局评分数量信息的相似度，主要由目标用户的共同评分项目相对于其所有评分项目的比例构成。不仅强调共同评分项目的重要性，而且考虑单个用户的所有评分项目信息。由于用户间的评分数量大多数情况下不相同（即Iu≠Iv），则考虑全局评分数量信息的用户间相似度一般不对称（即sim(u,v)≠sim(v,u)），说明用户间影响力不是同等重要的，更加符合用户间实际的影响力情况。同时由于用户评分数据是离散的，用户间的关系一般不是线性的，选用非线性Sigmoid 函数更好地衡量用户间的关系，同时惩罚低相似度，奖励高相似度。最终基于用户全局评分数量信息的相似度公式如式（6）所示，不仅反映用户自身的全局偏好，而且有助于在预测模型中选择合适的最近邻进而提高评分预测的准确性。

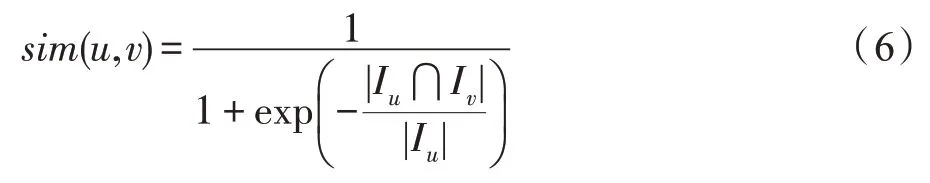
2.2 预筛选模式

基于邻域的协同过滤算法最主要的性能瓶颈是查找邻居集的过程十分耗时。如果该性能问题可以得到缓解，会比常规模式下有更高的计算效率。受上述相似度模型和评分预测公式中隐式约束的启发，提出预筛选模式。目的是在不影响预测和推荐结果的前提下，有效检索出对预测评分值有贡献的用户，同时过滤掉其余不参与计算的用户及对应的评分数据。

基于相似度模型和评分预测公式的固有特性，提出以下筛选条件：（1）对任意两个用户u和v，如果Iu⋂Iv=∅（即两个用户间没有共同评分项目），则相似度为0。（2）对于目标用户u和目标项目i，若rv,i不存在（即邻居用户未对目标项目有评分行为），则评分预测不可计算。

根据筛选条件（1），可以安全地忽略掉那些对目标用户已评分物品没有评分行为的用户。根据筛选条件（2），可以忽略掉那些对目标物品没有评分行为的用户。这两类用户都可通过访问预构建的项目-用户表轻松获得，因此只有同时满足与目标用户有共同评分，且对目标物品有评分行为的用户才能进入备选邻居集（将满足上述筛选条件的两类用户集合取交集，即可获得目标用户的备选邻居集）。因此目标用户只需与备选邻居集中的用户计算相似度，在不影响预测准确度和推荐质量的情况下，缩小邻居的查询范围，从而实现高效的推荐。

2.3 讨论

2.3.1 讨论相似度模型

根据提出的相似度模型（SES），为得到用户u和v的相似度，需根据公式依次计算sim(u,v)RAD、sim(u,v)ENT和sim(u,v)GRN。根据表1 中示例数据计算用户相似度，结果如表2 所示。

表1 用户-物品评分矩阵实例Table 1 Example of user-item rating matrix

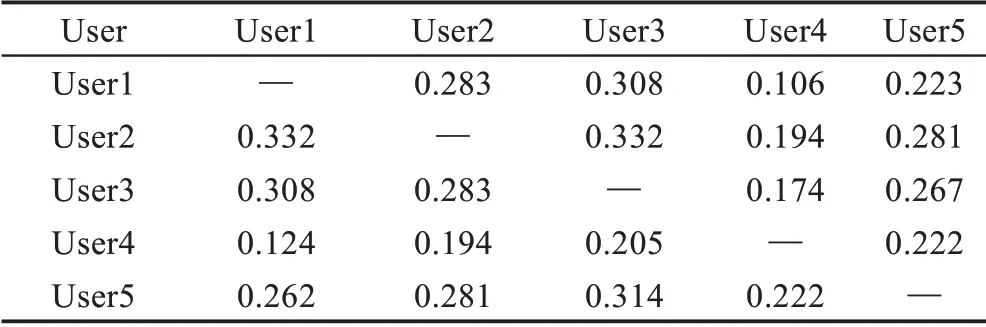
表2 用户相似度计算结果Table 2 Values of user similarity

可以看出：（1）无极端相似度值的产生。由于相对评分差异本身的取值较广泛，且通过加入较合适的函数进一步优化计算的结果值，不仅能够避免极端相似度值的产生，而且使用户间相似度值分布在较合理的范围内。（2）相似度值分布均匀。用户的评分均值和信息熵大多不同，使得用户间相似度值具有可比性。同时评分偏好的计算返回值较小，可减弱用户评分偏好对相似度的影响。（3）相似度值是非对称的。用户间的相似度基本是不一致的，更加符合用户间相似度的实际情况。因此示例中得出的相似度结果验证了提出的相似度模型具有的计算优势。

2.3.2 算法分析

最终融合相似度和预筛选模式的协同过滤算法（combined score enhanced similarity，CSES）的具体实现过程如算法1 所示。

算法1融合相似度和预筛选模式的协同过滤算法

假定数据集中用户和物品的数量分别是|U|和|I|，每个用户平均评价的物品数量为m，与目标用户存在共同评分项目的平均用户数量为|V|，两个用户间平均共同评分项目数量为n。

传统相似度（PCC、COS 等）需计算目标用户与原始邻居集中用户间的相似度，时间复杂度为O(|U|·|V|·n)。改进算法BCF 和KLCF 的时间复杂度主要分为两部分，首先计算任意两个物品间的相似度，复杂度为O(|I|·|I|)，然后计算用户相似度，任何两个用户间的相似度计算是基于笛卡尔积操作，复杂度为O(|U|·|U|·m·m)，因此总时间复杂度为O(|U|·|U|·m·m+|I|·|I|)。改进算法RJMSD 计算相似度时考虑用户的所有评价向量，时间复杂度为O(|U|·|U|·m)。本文提出的协同过滤算法（CSES）只需计算目标用户与备选邻居集中用户间的相似度。假设备选邻居集中的平均用户数量为|S|（|S|远小于|V|和|U|），目标用户与备选邻居集中用户间的平均共同评分物品数量为k，时间复杂度为O(|U|·|S|·k)。根据以上分析，CSES的时间复杂度最低，且随着数据规模的增加，CSES的时间复杂度有更突出的优势。

3 实验

为验证本文提出的协同过滤算法的有效性，选择4种经典的算法（SPCC[11]、COS[6]、Jaccard[9]、JMSD[10]）以及4种不同的改进算法（NHSM[16]、BCF[17]、KLCF[18]、RJMSD[26]）作为对比实验。所有的实验均在开发平台AI Studio 上运行，其中处理器为4 核，主存为32 GB，开发语言为Python3.7，框架版本为PaddlePaddle 2.0.2。为减少实验环境的影响，采用5 次实验的平均值作为统计的结果。

3.1 数据集

实验选择常用的三个公开数据集，其中两个来自MovieLens，分别是ML-100K 和ML-Latest-Small，另一个是Yahoo Music。表3 总结了各数据集在用户、物品、评分和稀疏度[32]方面的属性。为评估算法的性能，遵循经典的推荐系统测试方法[33]，在数据集中随机选取每个用户80%的评分数据作为训练集，其余作为测试集。

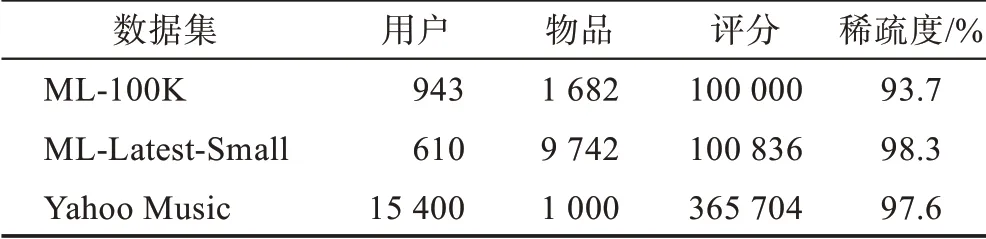
表3 数据集属性Table 3 Properties of datasets

3.2 评测指标

使用预测准确性和推荐准确性衡量推荐算法的质量，使用覆盖率评价推荐算法挖掘长尾的能力。

预测准确性的常用指标是平均绝对误差（mean absolute error，MAE）和均方根误差（root mean squared error，RMSE），用于评估测试集中实际评分值和预测评分值的差异，误差越低表示预测准确性越好。MAE 和RMSE 的公式如式（7）、式（8）所示。

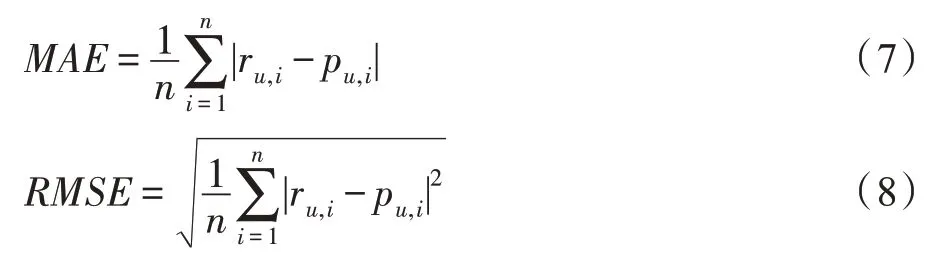
其中，ru,i、pu,i分别为目标用户对目标物品的实际评分和预测评分，n表示算法执行预测的次数。

推荐准确性包括三个重要的指标，精确率（Precision）、召回率（Recall）和综合评价指标（F1-value），如式（9）～式（11）所示。其中F1-value 同时考虑精确率和召回率，F1-value越高，表示推荐的质量越好。

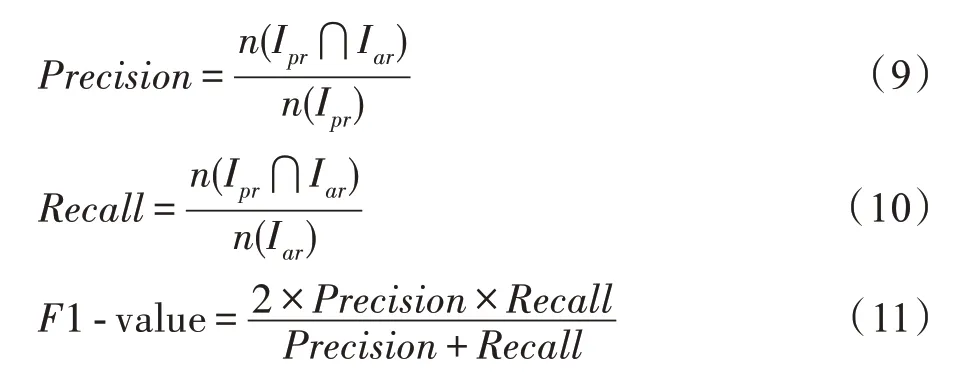
其中，Ipr和Iar分别是预测推荐列表和测试集中实际推荐列表，n(·)表示返回集合中元素的个数。采取的推荐规则是：出现在推荐列表中物品的评分必须大于该目标用户的平均评分。

覆盖率（Coverage）定义为推荐系统能够推荐出的物品占总物品的比例。覆盖率越高说明推荐算法发掘长尾的能力越好，如式（12）所示，其中Iut是测试集中实际的评分列表。

3.3 实验结果和分析

3.3.1 预筛选模式的有效性分析

通过理论上对相似度模型和评分预测公式的分析，提出预筛选模式。首先在三个数据集上分别进行实验，对比原始邻居集和使用预筛选模式后得到的备选邻居集中的平均用户数量，预筛选的效果如图1所示。

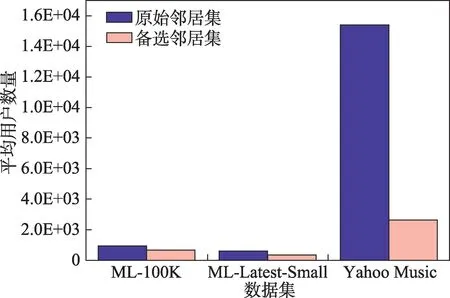
图1 原始邻居集和备选邻居集的平均用户数量对比Fig.1 Average number of users in original neighbor set versus alternative neighbor set

在ML-100K 数据集中，原始邻居集的平均用户数量为943，而备选邻居集的平均用户数量约为668，使用预筛选模式后，共过滤29.16%的用户和相应的评分数据。同样，在ML-Latest-Small 数据集中，原始邻居集的平均用户数量为610，备选邻居集的平均用户数量约为351，过滤了42.46%的用户和相应评分数据。在Yahoo Music 数据集中，原始邻居集的平均用户数量为15 400，备选邻居集的平均用户数量约为2 635，共过滤82.89%的用户和相应评分数据。从各数据集过滤的用户和评分数据的百分比可以看出，预筛选模式能减少大量的用户相似度计算，并且在稀疏数据集中的效果更加突出。

为进一步细化分析预筛选模式对时间效率的影响，在三个数据集上，分别统计提出的相似度模型（SES）在常规模式和预筛选模式下完成单次推荐所需的平均时间，主要分为查找邻居集和完成评分预测的时间。其中近邻个数根据文献[30]设为80，结果如表4 和表5 所示。

根据表4 和表5 中各部分的时间对比，首先在查找近邻的步骤中，预筛选模式相比常规模式在三个数据集上分别提升36.88%、22.84%和71.55%的时间效率。其次在产生预测的步骤中，执行时间无明显差别。最后在三个数据集上，预筛选模式的总运行时间相比常规模式分别下降35.42%、20.29%和71.18%。以上分析证明了预筛选模式的有效性，特别在规模较大的数据集中，预筛选模式的优势更加突出。因此引入预筛选模式后，SES 的时间效率得到进一步提升。

表4 常规模式下单次推荐所需时间Table 4 Running time for single recommendation in common mode 单位：s

表5 预筛选模式下单次推荐所需时间Table 5 Running time for single recommendation in pre-filtering mode 单位：s

3.3.2 整体预测和推荐效果比较

在三个数据集上分别进行实验，主要讨论不同近邻数量下融合预筛选模式后的协同过滤算法（CSES）与其余对比算法的预测和推荐结果。其中近邻数量从10 到100 变化，步长为10。

（1）在ML-100K 数据集上的结果分析

在ML-100K 数据集上，各算法的预测准确度如图2 所示。图2 表明，随着近邻个数的增加，所有方法的预测误差（MAE 和RMSE）值都逐渐下降。其中SPCC、BCF、KLCF 的预测误差值较高，且波动范围较大。COS、JMSD、RJMSD 的预测准确度有明显改善，且变化趋势较为接近。不同近邻数量下，CSES具有最好的预测准确度，相比最接近的NHSM 平均降低1%～2%的预测误差，特别在近邻个数较少时，优势更加明显。主要原因可能为：基于exp(-x)函数衡量相对评分差异的相似度能更敏感地捕捉评分差异的变化，同时综合信息熵改进的评分偏好和用户的全局评分数量信息，使相似度计算更加可靠。

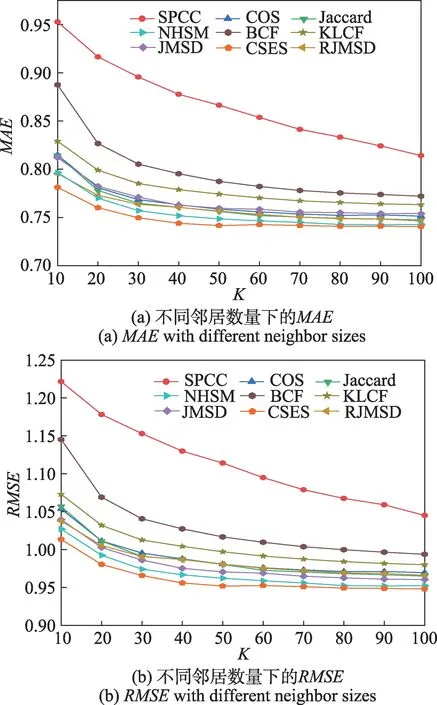
图2 ML-100K 数据集上不同邻居数量的MAE 和RMSEFig.2 MAE and RMSE with different neighbor sizes on ML-100K dataset

在ML-100K 数据集上，各算法的推荐质量如图3所示。所有方法的F1 值都随近邻数量的增加而逐渐变大。其中最近提出的算法BCF、NHSM、KLCF 相比传统算法在推荐质量方面有明显的改善。当近邻个数为10 时，CSES 的F1 值略低于BCF，但随着近邻数量的增加，CSES 的F1 值最高且有相对稳定的表现，当近邻数量为100 时，CSES 的F1 值达到最大值，约为0.696。因此在ML-100K 数据集上，CSES 相比其他算法有更好的推荐质量。

图3 ML-100K 数据集上不同邻居数量的F1-valueFig.3 F1-value with different neighbor sizes on ML-100K dataset

在ML-100K 数据集上，各算法的覆盖率如图4所示。在不同邻居数量下，CSES 的覆盖率略低于BCF，保持最接近的趋势且相对稳定。相比其余算法，CSES 和BCF 均有更好的覆盖率。BCF 的覆盖率较高，原因可能为：能够计算任意两个用户间的相似度，得到的预测推荐列表中有效评分数量更多，因此覆盖率会略有优势。

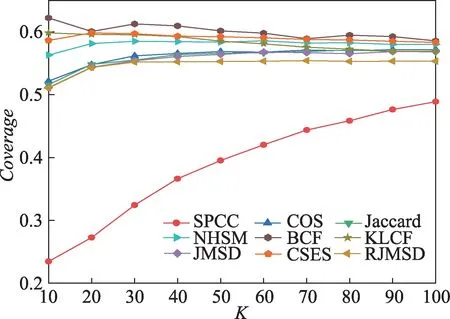
图4 ML-100K 数据集上不同邻居数量的CoverageFig.4 Coverage with different neighbor sizes on ML-100K dataset

（2）在ML-Latest-Small数据集上的结果分析

同样地，在ML-Latest-Small 数据集上执行所有算法，预测准确度如图5 所示。在不同近邻数量下，CSES 都有最好的预测准确率和较小的波动范围，相比最接近的NHSM 和RJMSD 大约提升1%～3%。所有算法在ML-Latest-Small 数据集上的误差范围均比在ML-100K 上有所降低，主要因为：在评分数量相差不大的情况下，ML-Latest-Small 数据集上的用户数量相对较少，则单个用户对应的评分数据更多，基于用户的相似度计算就更加准确。

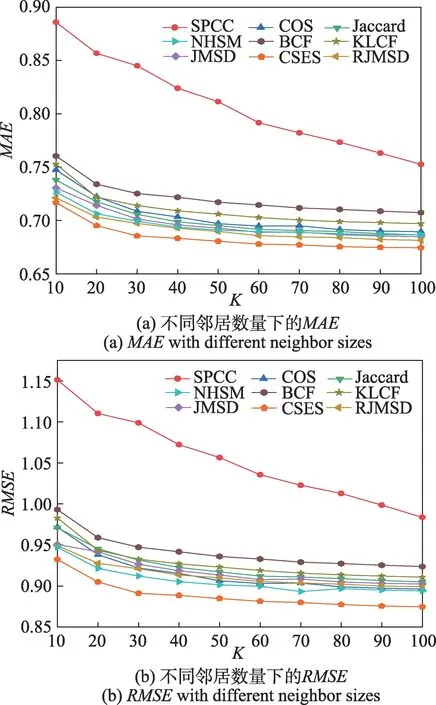
图5 ML-Latest-Small数据集上不同邻居数量的MAE 和RMSEFig.5 MAE and RMSE with different neighbor sizes on ML-Latest-Small dataset

在ML-Latest-Small 数据集上执行所有算法，推荐质量如图6 所示。不同近邻数量下，CSES 都有最高的F1 值。相比表现较好的BCF、KLCF、NHSM，平均提升1%～3%。随着近邻数量的增加，BCF、KLCF、NHSM 的F1 值无显著差异。

图6 ML-Latest-Small数据集上不同邻居数量的F1-valueFig.6 F1-value with different neighbor sizes on ML-Latest-Small dataset

在ML-Latest-Small 数据集上，各算法的覆盖率如图7 所示。不同近邻数量下相比其余算法，BCF、KLCF 和CSES 的RMSE覆盖率较高，且分布区间为[0.580,0.603]。随着近邻数量的增加，三者MAE的差距越来越小。

图7 ML-Latest-Small数据集上不同邻居数量的CoverageFig.7 Coverage with different neighbor sizes on ML-Latest-Small dataset

（3）在Yahoo Music数据集上的结果分析

在Yahoo Music 数据集上执行所有算法，预测准确度如图8 所示。在不同近邻数量下CSES 的预测误差值最低，相比表现较接近的NHSM 和RJMSD 降低大约1%～4%，相比其余算法则有更明显的优势。在Yahoo Music 数据集上，所有算法的预测误差值都普遍较高，主要原因是：数据规模明显变大且用户数量也明显变多，单个用户对应的评分数据较少，因此预测误差值较高。

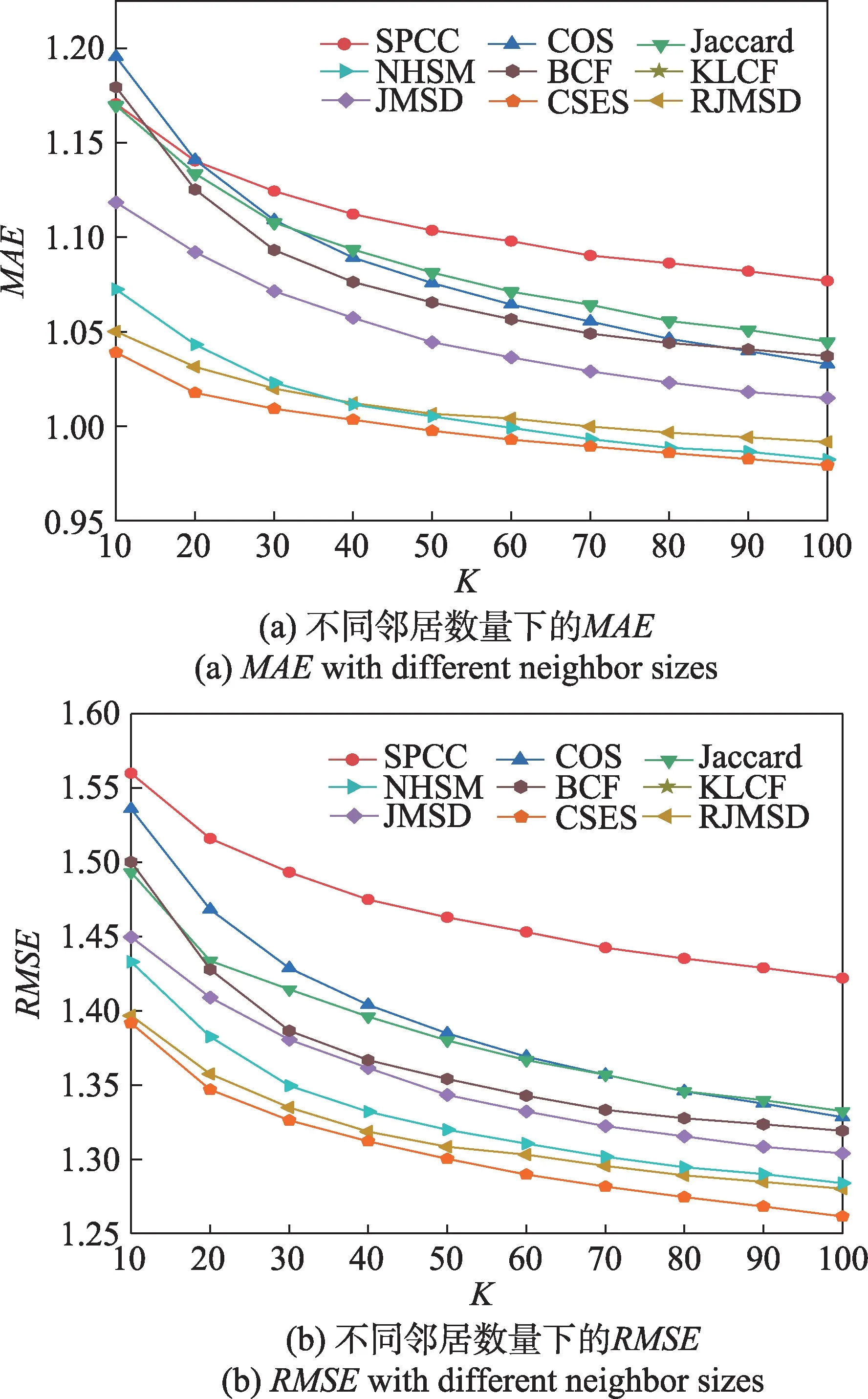
图8 Yahoo Music数据集上不同邻居数量的MAE 和RMSEFig.8 MAE and RMSE with different neighbor sizes on Yahoo Music dataset

在Yahoo Music 数据集上各算法的推荐质量如图9 所示。不同邻居数量下，CSES 比其余方法有更好的推荐质量，特别在邻居数量较少时，这种优势更加明显。其中，NHSM、RJMSD、BCF 和SPCC 的推荐质量相比其余传统方法也有较大提升。

图9 Yahoo Music数据集上不同邻居数量的F1-valueFig.9 F1-value with different neighbor sizes on Yahoo Music dataset

在Yahoo Music 数据集上，各算法的覆盖率如图10 所示。当近邻个数小于30 时，BCF 的Coverage 值最高，与最接近的CSES 相比有2%～3%的优势；当近邻个数大于30 时，CSES 的coverage 值最高，相比最接近的RJMSD 提升1%～4%。

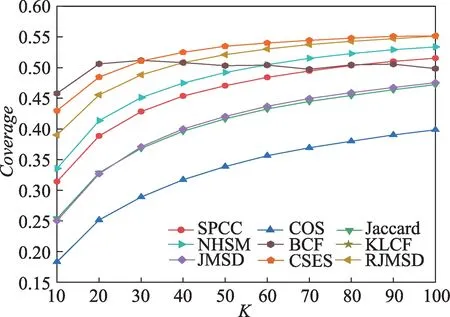
图10 Yahoo Music数据集上不同邻居数量的CoverageFig.10 Coverage with different neighbor sizes on Yahoo Music dataset

3.3.3 时间效率比较

在三个数据集上，分别统计各评测指标中表现较好的5种算法（CSES、RJMSD、NHSM、BCF和KLCF）的总运行时间，具体结果如表6 所示。

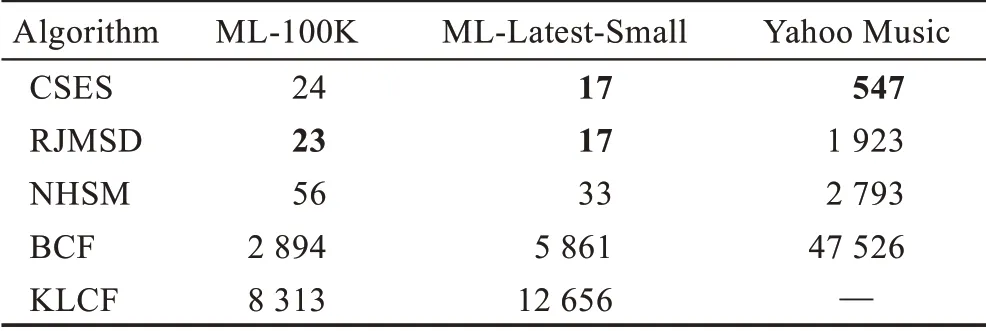
表6 在三个数据集上的总运行时间对比Table 6 Running time comparison on three datasets 单位：s

从表6 中可以看出，在ML-100K 数据集上，CSES和RJMSD 的总运行时间无明显差别，相比NHSM 分别有大约57.14%和58.93%的降低。同样地，在MLLatest-Small 数据集上，CSES 和RJMSD 的总运行时间一致，相比NHSM 大约降低48.48%。在Yahoo Music 数据集上，CSES 的总运行时间最短，相比RJMSD 和NHSM 大约降低71.55%和80.42%。然而在三个数据集上，BCF 和KLCF 的总运行时间较长，与CSES、RJMSD 和NHSM 相比有明显的差距。综合以上分析，CSES 的时间效率较高，特别在稀疏数据集下优势更加突出。

4 结束语

本文提出将相似度和预筛选模式融合的协同过滤算法，以更好地平衡准确性和时间效率的关系。该算法首先定义相对评分差异，并根据相似度函数应满足的条件得到基于相对评分差异优化的相似度，能更敏感地捕捉用户间评分变化。同时将基于信息熵改进的评分偏好和基于用户全局评分的数量信息作为权重因子，更易区分用户间相似度。提出的相似度模型具有简单高效的特性，并缓解了稀疏数据下推荐准确性问题。其次通过分析相似度和评分预测公式的隐式约束，进一步提出预筛选模式。在不影响预测和推荐结果的前提下，减少大量无效的相似度计算，极大地改善了算法运行效率。最终提出的协同过滤算法融合相似度和预筛选模式，在三个不同稀疏度的数据集上实验，结果表明：相比已有算法，所提出的算法在保持相对稳定和较高推荐准确性的同时，进一步提高了系统运行效率。

本研究仅关注评分矩阵中评分数据，未来的工作将分析评分表以外的物品标签、用户评论等信息，进一步提升推荐性能。