类不平衡数据的EM 聚类过采样算法
谢子鹏,包崇明,周丽华,王崇云,孔 兵+
1.云南大学信息学院,昆明650504
2.云南大学软件学院,昆明650504
3.云南大学生态学与环境学院,昆明650504
分类问题几乎出现在日常生活的各个方面,被认为是人类最常执行的决策功能。分类问题是机器学习、深度学习、数据挖掘等领域不可缺失的一部分,分类任务存在于绝大多数应用当中,如人脸识别任务[1]、风险管理[2]、欺诈检测[3]、污染检测[4]、医学诊断[5]以及各种数据的分类任务[6-7]。只有正确地将数据分类之后,才能通过数据挖掘、数据分析等方法挖掘信息的潜在价值。
现有的分类算法有很多,如决策树分类算法[8]、线性分类算法[9]、朴素贝叶斯分类算法[10]、KNN(Knearest neighbor)分类算法[11]、SVM(support vector machine)分类算法[12]等。这些算法处理平衡的二分类问题比较有效,但是对于不平衡的二分类数据集,不能很好地拟合少数类数据,导致所训练的分类器分类效果不佳[13-14]。
数据级方法[15-16]是最常用于解决类不平衡问题的方法。数据级方法通过减少多数类样本数量或者增加少数类样本数量来使样本平衡[17],直接解决类不平衡问题的根源,并且不被特定的分类模型限制[18-19]。数据级方法包括三个方向,即过采样方法[20]、欠采样方法以及混合方法[21-22]。其中,过采样方法比其他数据级方法更常用,Batista 等人实验结果表明,以ROC曲线下的面积衡量,过采样的效果通常比欠采样好[23]。
现有的数据级过采样技术有许多,但是采样方式大多属于随机采样。SMOTE(synthetic minority over-sampling technique)过采样算法[15]被认为是最有影响力的数据采样算法,SMOTE 的思想是通过在相邻的少数类样本之间进行随机插值过采样,从而平衡原始的训练数据。由Georgios 等人提出的Cluster-SMOTE[24]的做法是首先对整个样本空间进行聚类,通过选取多个聚类空间中少数类样本占比最大的空间进行过采样,但是该方法的聚类空间数量以及对每个簇中生成新样本的数量都无法很好确定。Han等人提出的Borderline-SMOTE[20]仅对靠近边界线的少数实例进行过采样。NRSBoundary-SMOTE[25]使用粗糙集理论查找边界区域并对边界区域中的少数实例进行过采样。Lin等人提出较为新颖的基于Cluster的欠采样[26],对多数类样本进行聚类,但是该算法将聚类数量盲目设置为少数类样本数量,选取聚类中心作为欠采样样本点,在不平衡率较高的数据集上会损失大量多数类样本点信息,该方法只适用于不平衡率较低的数据集。
为了克服过采样的局限性,并且使过采样得到更真实样本点,本文使用聚类算法来代替随机过采样策略,提出了一种EM(expectation-maximization)聚类过采样算法(oversampling based on EM-clustering,OEMC)。聚类算法可将空间中样本以某种相似性划分为同一簇,而EM 聚类可产生最能够代表该簇特性的样本,即称为簇中心点,对少数类进行聚类,以簇中心点作为过采样的样本。为了避免盲目追求两类样本数量平衡而导致分类性能下降,即避免盲目采样问题,将新增样本点占少数类样本的比例称为采样率,通过实验选取不同的采样率得到能够在普遍数据集上使得分类性能最佳的采样率。具体来说,通过对少数类样本按照最佳采样率,过采样得到每个簇的中心点作为最有代表性的样本点添加到训练集中,从而增加少数类样本数量,达到降低数据不平衡率[27]的目的。
本文的主要贡献如下:为了解决类不平衡问题,提出了一种新的数据级过采样算法。首先,本文提出的算法采用聚类技术,通过欧氏距离衡量样本间的相似度,选取每个聚类簇的中心点作为过采样点,解决了样本的重要程度不够的问题;其次,该算法通过直接在少数类样本空间上进行采样,解决了SMOTE、Cluster-SMOTE 等方法对聚类空间没有针对性的问题;最后,该算法通过对少数类样本数量的30%进行过采样,解决了基于Cluster聚类的欠采样盲目追求两类样本数量平衡和SMOTE 等算法没有明确采样率的问题,并且算法具有较好的效率。
1 相关工作
1.1 类不平衡问题
实际应用中,将多数类错误分类为少数类产生的损失与将少数类错误分类为多数类产生的损失可能会有所不同。如在医疗领域中,将存在疾病的患者错误判断为健康的人造成的损失显然远大于将健康的人错误判断为存在疾病造成的损失。健康的人可以视为多数类,疾病患者可以视为少数类,生活中通常关注的重点也是类不平衡问题中的少数类。如果不考虑类不平衡问题,分类学习算法构建的模型可能会对多数类过拟合,而忽略少数类。考虑一个失衡比例为99%的二分类数据集,其中,多数类样本占数据集的99%,少数类样本仅为1%。为了使错误率最小化,学习算法以相同的错误分类损失将所有样本归为多数类[28],模型的分类错误率仅为1%。但是这显然是没有意义的。
在数据分布不规则的数据集中,类不平衡是其中的一种表现。该问题具有以下特征[29]:
(1)样本量小:在不平衡问题中,少数类样本往往缺失,而多数类包含大量样本,导致构建的分类器的分类结果严重倾向多数类。最根本的解决方案就是通过增加少数类样本或减少多数类样本从而降低不平衡率。
(2)类别重叠:当属于不同类样本在数据空间中发生重叠时,分类器很难有效区分不同类别。如果数据没有类别重叠问题,那么任何简单分类器可以通过适当的学习达到不错的效果,如图1 所示。

图1 类别重叠示例Fig.1 Example of class overlapping
(3)小分裂群:当少数类样本分裂状地分布在多个特征空间中,在分类任务中,这种情况会增加问题的复杂度,如图2 所示。

图2 小分裂群示例Fig.2 Example of small disjuncts
类不平衡问题包含以上三种特征,这些特征也是许多真实的类不平衡数据集在样本空间上分布的特点,通过以上二维不平衡数据分布示意图可以类比高维数据,解决类不平衡问题的关键是需要考虑重采样样本点的空间分布的合理性。
1.2 数据级采样方法
不平衡数据集的分类问题已经研究了很多年,现有的数据级解决方式也有很多,这些方法都有各自的优点,都解决了不同方面的相关问题。并且数据级方法的使用也更加通用,可以独立于基本的分类器[29]。
1.2.1 基于聚类的欠采样算法
Lin 等人提出的基于聚类的欠采样算法是用于解决类不平衡问题的一种数据级采样算法[26]。该方法的主要思想是,通过聚类方式对多数类样本进行聚类,将聚类簇的数量设置为少数类样本数量,通过选取簇的中心点作为欠采样样本点,以欠采样的样本点代替原始多数类训练数据,从而达到两类样本数量相等的目的。该方法的缺点是它盲目追求两类样本数量平衡,但是当失衡率高的情况下,欠采样会丢失大量数据信息,使得采样点发生类别重叠与小分类群的问题。
1.2.2 SMOTE 算法
由Chawla 等人提出的综合少数类过采样技术(SMOTE)被认为是最有影响力的数据过采样算法[15]。其基本思想是在少数类样本连线之间进行随机插值过采样,该算法增加了少数类样本数量以提高分类器的性能。
1.2.3 Cluster-SMOTE 算法
由Georgios 等人提出的Cluster-SMOTE 算法是基于SMOTE 算法改进的解决类不平衡问题的数据级算法[24]。该方法的主要思想是,首先通过K-means聚类将输入空间聚类为k个组,保留含有较多少数类样本的簇,对这些保留的簇采取SMOTE 算法对少数类过采样,将过采样数据添加到训练集从而达到降低失衡率的目的。该方法的缺点是无法确定k的大小,k的大小直接影响过采样的质量,并且聚类空间没有限制,聚类后的簇中会包含多数类样本,这将产生一定程度噪声点。
总而言之,最近有很多旨在解决类不平衡问题的数据级算法,并且取得了很多方面的成功。但是这些算法都存在自身的问题,虽然解决了类别数量不平衡问题,但是产生的新样本存在类别重叠问题,以及许多技术以高复杂度的代价来解决现有问题,使得这些技术难以实现与使用[24]。
2 EM 聚类过采样算法
本文提出基于EM聚类的过采样算法OEMC(oversampling based on EM-clustering)。算法采用聚类技术对样本过采样,从而得到更有意义的样本点。聚类过程中,过采样得到的新样本可视为隐变量,而最大期望算法的思想正是求解隐变量的方法,通过逐步迭代,使聚类中心点不断调优,最后得到最有代表性的样本点。所提出的方法首先划分少数类样本空间与多数类样本空间,然后基于OEMC 算法在少数类样本空间生成新样本,最后得到新的数据集。该算法包含的划分类别空间与过采样步骤目的在于解决上述的不平衡问题包含的三类子问题,其中划分类别空间的目的是为了避免过采样产生的样本发生类别重叠以及小分裂群的问题,使用聚类过采样是为了降低类别不平衡问题。
为了说明SMOTE过采样算法、Cluster-SMOTE过采样算法、Cluster欠采样算法以及本文提出的EM聚类的过采样算法解决具体的不平衡问题时的采样合理性,列举了四种算法的采样效果示意图,如图3所示。
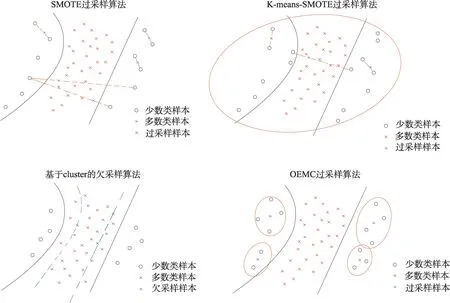
图3 四种采样算法示意图Fig.3 Schematic diagram of four sampling algorithms
从图3 可看出,线性插值法SMOTE 算法以及Kmeans-SMOTE 算法在某些情况产生的过采样样本点会分布于多数类样本空间中;而基于Cluster 的欠采样算法由于将重采样样本点代替原多数类样本点,导致多数类与少数类样本边界发生偏离,产生类别重叠情况;而本文提出的EM 聚类过采样算法通过对少数类样本空间聚类,选取中心点作为过采样点,可以很好地解决新增样本的空间分布问题。
2.1 算法描述
EM 聚类过采样算法主要分为以下步骤:首先将原始数据通过分层随机采样划分为80%的训练集与20%的测试集,分层采样可保持数据集的不平衡率,具体的做法是分别从两个类别中抽取各自的80%后组成训练集,剩余的作为测试集;然后从训练集按照类别标签划分多数类样本空间与少数类样本空间;在少数类样本空间中按照一定的采样率用基于EM聚类算法的过采样产生新样本,采样率需要通过实验调整;将新样本与训练集组合,得到不平衡率降低的训练集。OEMC 算法的数据处理流程为图4 所示。

图4 OEMC 算法过采样流程Fig.4 Data oversampling procedure of OEMC
所提出的方法与之前提到的相关技术的不同之处在于,该方法不必考虑整个样本空间,直接针对划分类别空间后的少数类样本空间进行过采样。而且通过对过采样率的调整,可以很大程度上防止算法产生不具代表性的样本与噪声点,最大程度地提高分类器对数据的泛化能力。该算法的过采样步骤不盲目追求类别间样本数量相近,在越高维的数据与不平衡率越高的数据集上的效果越好。
2.2 EM 算法
EM 算法又称为期望最大化算法,该算法受到缺失思想影响,最初是为了解决数据缺失情况下的参数估计问题,其算法基础和收敛有效性等问题由Dempster给出了详细的阐述[30]。EM 算法是最常见的隐变量估计方法,在机器学习中有广泛的用途,是一种迭代优化策略算法。该算法的思想分为两步,即E(期望)步与M(极大化)步。首先根据己经给出的观测数据,估计出模型参数的值;然后依据上一步估计出的参数值估计缺失数据的值;再根据估计出的缺失数据加上之前己经观测到的数据重新对参数值进行估计,反复迭代,直至最后收敛,迭代结束。
算法1EM 算法

2.3 Cluster_EM 算法
该算法采用最大期望化思想求解聚类中心点。
算法2EM 聚类算法(Cluster_EM)流程

2.4 OEMC 算法
本文提出的EM 聚类过采样技术(OEMC)通过聚类算法增加符合真实数据分布的样本点数量解决类不平衡问题。
式(1)与式(2)给出样本相似度衡量的两种方式:


算法3OEMC 算法流程
输入:不平衡数据集D,聚类算法Cluster_EM,过采样率OversamplingRate,随机采样策略stratifiedSampling,相似度衡量标准Standard=Similarity_European。
输出:过采样后的数据集D′。
1.data_train,data_test←stratifiedSampling(D)
2.minority,majority←Classify(data_train)
3.k←OversamplingRate×Num(minority)
4.while average_similarity(minority,K_center)>0.8 do
5.K_center←initializeCenter(minority,k)
6.K_center←Cluster_EM(minority,k,Standard)
7.end while
8.D′←D+K_center
9.end
3 实验
3.1 数据集
本文使用两类真实的失衡二分类数据集进行实验:第一类数据集是Galar 等人使用的22 个小型数据集[29],这些数据集的不平衡比率(多数类样本数量与少数类样本数量的比值)在1.8~129,数据的特征数量在3~19,采集的数据样本数量在130~5 500;第二类数据集使用了Knowledge Discovery 和Data Mining Cup两个大型数据集,即乳腺癌和蛋白质同源性预测数据集,分别包含102 294 和145 751 个数据样本以及117 和74 个特征数量,两个数据集的不平衡比率分别约为163 和111。数据集信息描述见表1。
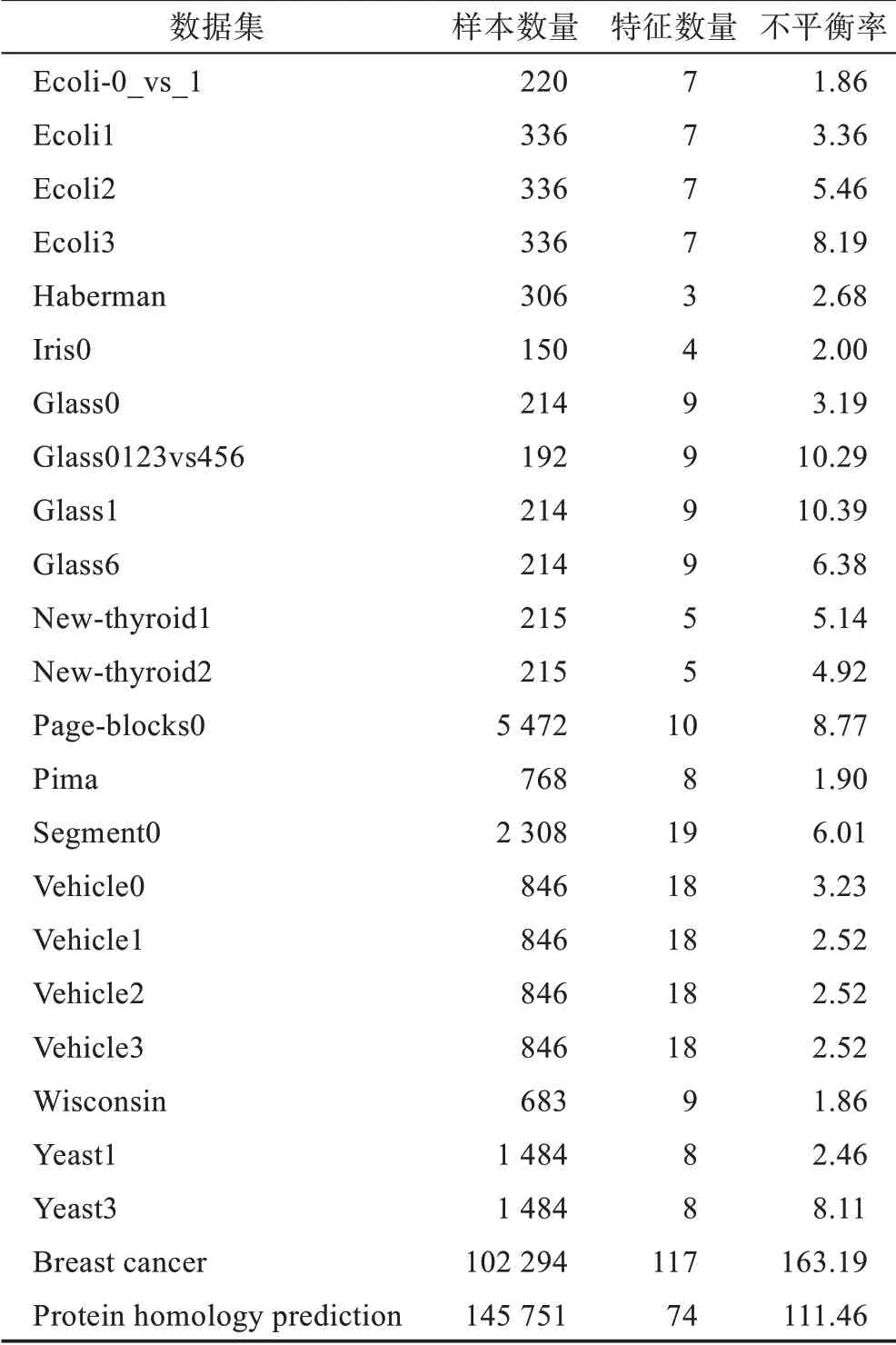
表1 数据集信息Table 1 Dataset information
3.2 实验设计
为了证明本文算法的有效性,将本文算法与目前现有的3 种解决不平衡数据集的算法进行比较。针对24 个数据集,采用原始数据集、基于聚类的欠采样、SMOTE 算法、Cluster-SMOTE 算法和EM 聚类过采样算法分别处理的数据集作为实验数据集,在C4.5 决策树算法上进行分类性能实验。为了减小实验误差,体现算法的真实性能,采用5 折交叉验证将所有数据集分为80%的训练集和20%的测试集,所有实验进行10 次实验后取平均值。
3.2.1 评价指标
传统分类通常用分类精度作为衡量算法有效性的指标,但分类精度可以反映分类器整体的分类效果,而不能反映少数类的分类精度。不平衡数据集中,少数类别的识别精度通常更为重要,因此分类精度不适用于不平衡数据。针对不平衡数据集的分类性能评估,目前尚没有公认的度量标准。而且,选择不同的评估指标,可以观察到非常不同的结果。
混淆矩阵又称为误差矩阵,是用于计算精度的工具,其中记录了每个类被正确和错误识别的数量,混淆矩阵在分类任务中被广泛使用,在各种不平衡数据集实验中都被采用[29],可以更有意义地对实验结果进行评价。混淆矩阵如表2 所示。

表2 二分类混淆矩阵Table 2 Confusion matrix of binary classification
表2 中,TP 为正确分类的正样本数量,TN 为正确分类的负样本数量,FP 为分类错误的正样本数量,FN 为错误分类的负样本数量。基于以上定义,可以定义几个基本性能指标。
3.2.2 分类算法
为了评估过采样算法,需要选择分类算法来构建分类器,以确保该算法的有效性。通过构建机器学习分类模型,验证模型对数据的拟合能力。本研究选择被广泛用于处理不平衡数据的C4.5 决策树作为分类器[31-32],原因如下:首先,决策树模型经常被作为验证分类结果的首选模型,决策树模型具有良好的数据泛化能力和快速的训练速度,并且决策树模型可作为基线分类模型;其次,上文已经提到数据级的分类方法不受限于具体的分类模型;最后,在Georgios等人[24]、Lin 等人[26]的相关实验中都使用了决策树模型。
3.3 实验结果与分析
为了选择适合普遍数据集的最佳采样率,实验选取一个不平衡率为111.46 的大型数据集和4 个不平衡率分别为10.29、8.11、5.46、1.90 的小型数据集代表不同程度的不平衡数据集,用本文提出的OEMC算法进行不同采样率下的分类性能敏感测试。不同采样率下的各个数据集的分类性能变化如图5 所示,从中可看出,0.30 的采样率在各个不平衡程度的数据集上效果都较优,因此本文选取30%的采样率作为适合OEMC 算法的最佳采样率。
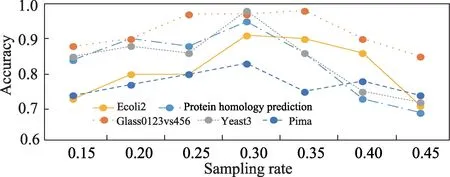
图5 采样率敏感测试Fig.5 Sampling rate sensitivity test
表3 显示了使用原始不处理的数据、基于聚类的欠采样算法处理的数据集、SMOTE 算法处理的数据集、K-means-SMOTE 算法处理的数据集以及本文提出的OEMC 算法处理的数据集在C4.5 分类器下的分类性能。表中精确度Accuracy 分为L 与M 列,分别代表少数类和多数类的Accuracy 指标。
从表3 可看出,本文提出的OEMC 算法与C4.5分类器结合在22 个数据集上都取得了最佳表现,特别是对少数类Accuracy 指标的提升明显超过3 种现有采样方法。该结果可以验证EM 聚类过采样算法可以增加少数类样本数量,从根本上解决类不平衡问题。通过结果可以看出,以欧氏距离作为样本相似度衡量标准的EM 算法产生了更有意义的样本点,并且证明了EM 聚类过采样算法对多种数据的普遍适用性,该方法可以有效解决数据不平衡带来的分类器性能低下的问题。
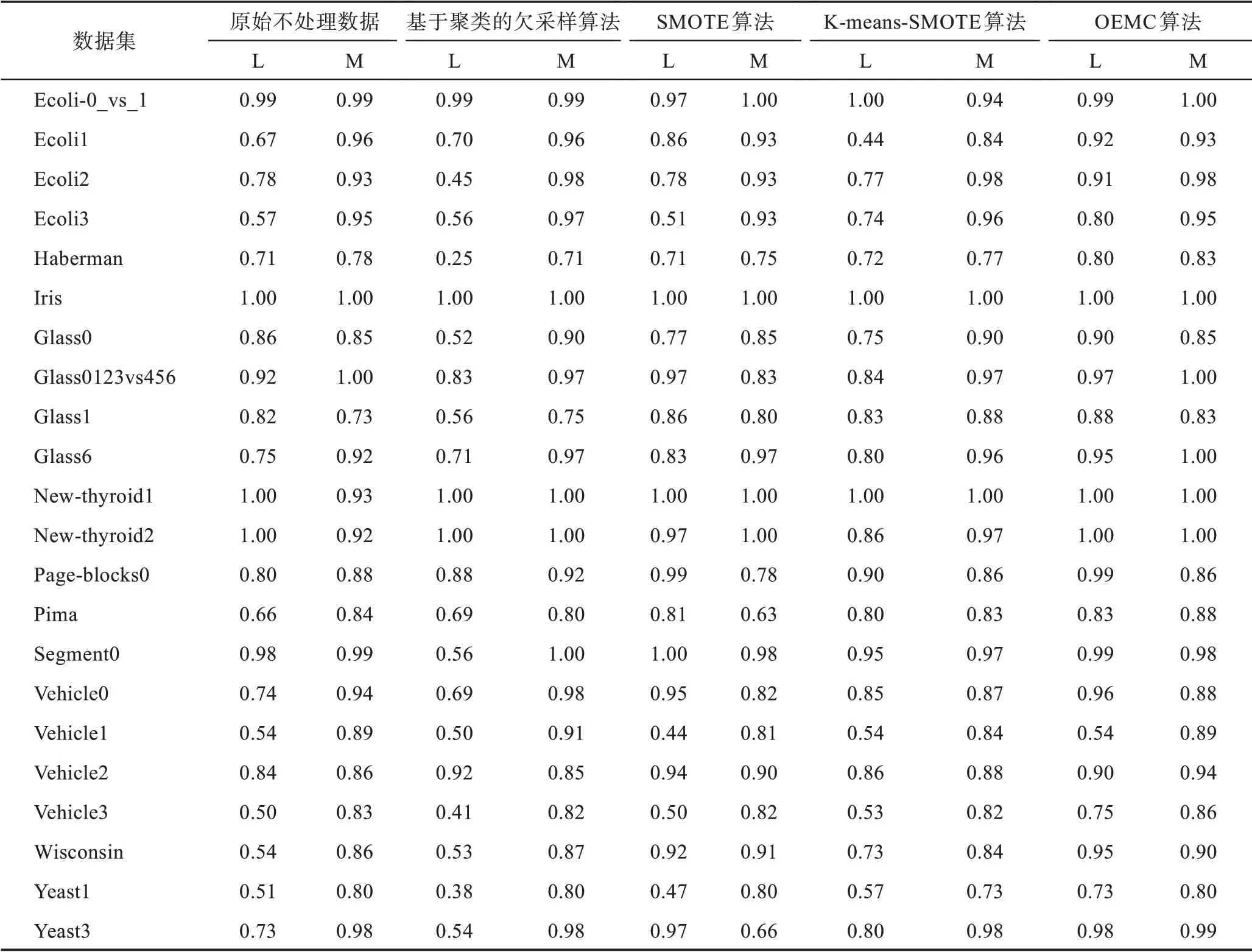
表3 C4.5 分类器与5 种数据处理方式结合的分类性能Table 3 Classification performance of five approaches with C4.5
图6 是5 种重采样方法在5 个小型数据集上的平均精确率的表现,平均精确率可反映分类器对数据的整体分类性能。Glass1、Yeast3 等5 种小型数据集是从上文提到的22 种小型数据集中按照不平衡率依次递减选取的有代表性的5 个数据集,每个数据集上统计了5 种方法的平均精确度。
从图6 可以看出,本文提出的EM 聚类过采样算法(oversampling based on EM-clustering)在5 个不平衡率依次递减的小型数据集上的表现最佳,并且获得的分数均在0.8 以上,同样采用了聚类方法的Kmeans-SMOTE 方法在小型数据集上的表现同样理想,再次证明了聚类方法对生成采样点有重要作用。

图6 5 种方法在5 个代表性小型数据集上的分类精确率Fig.6 Classification accuracy of five methods on five representative small datasets
图7 显示了对应上述表格中的5 种数据重采样方式在两个大型数据集上的实验结果,其中包含未处理的数据集(UD)、基于聚类的欠采样(UC)、SMOTE、K-means-SMOTE(KS)以及本文提出的OEMC 算法处理的数据与决策树分类器相结合在分类中得到的两个类别的精确率。

图7 5 种方法在两个大型数据集上的分类精确率Fig.7 Classification accuracy of five methods on two large datasets
从图7 可以看出,本文提出的EM 聚类过采样算法在平均精确率方面取得了最佳表现。从图中看出,基于聚类的欠采样以及SMOTE 算法过采样在蛋白质同源性预测数据集上都会导致类别重叠问题,类别边界偏移使得两类别特征模糊,最终分类器的性能下降。同样结合了聚类方法的K-means-SMOTE过采样算法在蛋白质同源性预测数据集上的精确率与本文算法的精确率相近。从图中可看出,K-means-SMOTE 算法在乳腺癌数据集上的精确率也仅略低于本文算法。因此将聚类方法结合到过采样算法中是十分重要的。
图8 比较了5 种重采样方法在两个大型数据集上的时间消耗实验结果。
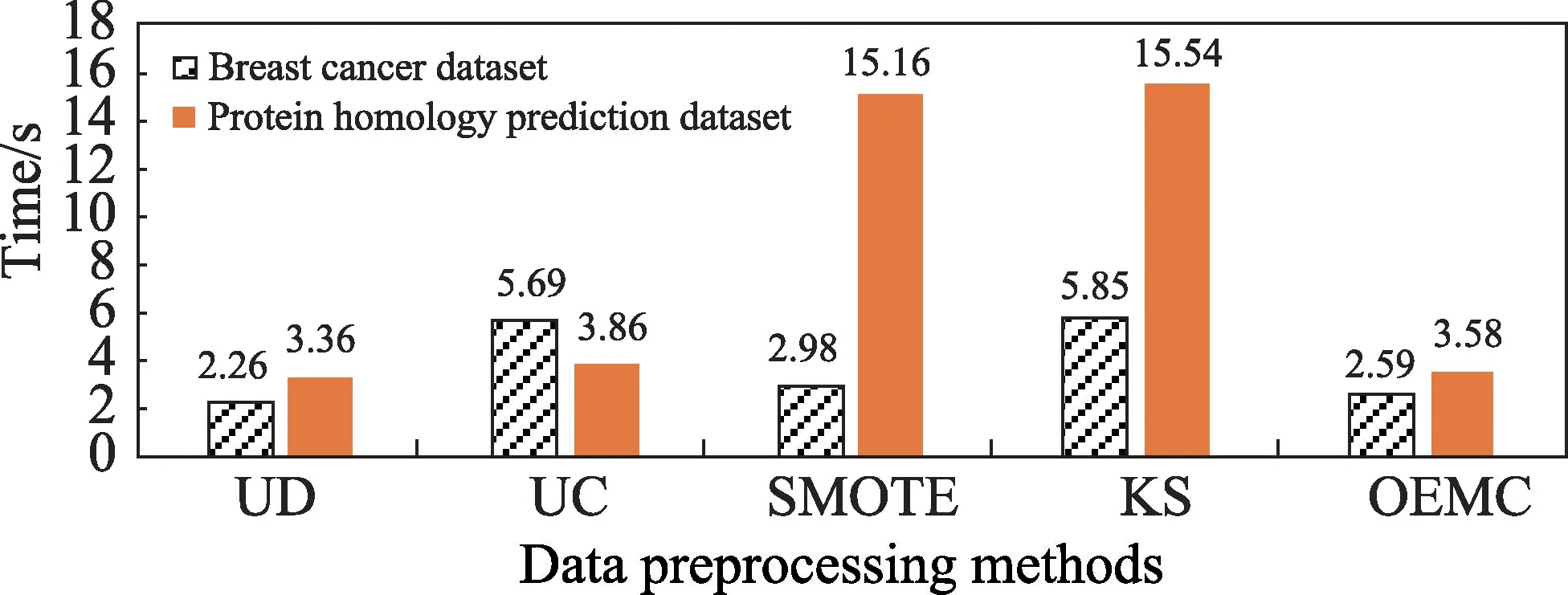
图8 5 种方法在两个大型数据集上的时间消耗Fig.8 Time consumption of five methods on two large datasets
从图8 可看出,由于本文提出的OEMC 算法设定的30%采样率,在时间消耗上仅次于未经数据重采样的方法,该结果表明选取最佳采样率不仅利于分类性能的提升,并且可以有效降低时间消耗。OEMC 的时间复杂度为O(m×n×d×e),其中m为过采样数量,n为少数类样本数量,d为数据维度,e为算法迭代次数。
4 结束语
当今数据不平衡问题给许多领域带来了困难,给许多分类算法带来了困难。
首先,对训练数据进行过采样以使其分布更均匀是在数据处理级别解决此问题的有效方法。一方面,随机过采样会导致过度拟合,从而降低模型在不可见数据上的分类性能;另一方面,如果不控制所生成的数据,则经常会生成带有噪声的样本,这会模糊样本边界并阻碍样本类型的确定。本文方法使用EM 聚类算法对初始少数类样本进行聚类,可以使得过采样样本点分布均匀,并能代表原始数据信息,可以防止由于过采样阶段中存在噪声样本而导致引入新的噪声。生成新样本时,根据采样率生成相应数量的少数类别样本。因为每个新生成的样本都与原始的少数类样本相关,所以不会生成异常值。
其次,在不平衡数据集的分类问题下,不平衡数据集不同类别的样本数量失衡比例过高,导致对分类器的训练过程中对少数类的拟合能力太差,对少数类的预测准确率低。本文方法可以降低不同类别样本数量的失衡比例,使得构造的分类器分类性能在24 个数据集上表现良好。
今后可以考虑两个问题:首先,由于原始数据存在噪声,多余的噪声导致分类器的性能不佳,今后可对本文提出的EM 聚类过采样算法的步骤中增加去噪步骤,例如通过支持向量机对初始数据进行去噪和初步分类。其次,可采取不同相似度衡量标准。采用不同的相似空间对数据过采样产生的结果会有明显差别。

