基于混沌映射的空域彩色图像复合加密算法

王 潇

(西安翻译学院 信息工程学院, 西安 710105)

0 引 言

伴随网络通信与多媒体技术的飞速发展, 受传播领域的传输模式影响[1-2], 图像信息安全不断产生新的问题, 某些保密数据无法直接在网络或信道内进行传输[3], 图像安全传输与储存变得尤为棘手。因图像的数据量多、 冗余性大、 像素关联性强[4]等特征, 其加密方法与文本加密算法有着本质区别。

针对图像加密问题, 史进等[5]利用安全哈希算法(SHA: Secure Hash Algorithm-256)方法处理初始明文, 采用去氧核糖核酸(DNA: Digital Network Architecture)编码进行编码操作, 通过迭代获取随机混沌矩阵, 使用光学调制掩码对密文进行光学加密。但该方法仅打乱了初始数据位置, 并没有更改图像统计特征, 极易受到选择明文攻击威胁。孙光民等[6]设计一种动态密码校验技术, 防止密码算法被字典或穷举方法破解, 运用魔方密码算法, 把像素与密码数据重新排列成六面体结构, 运用十字轴形式混淆图像数据, 实现图像加密任务。但该方法计算量过大, 且无法抵御剪切攻击, 实用性有待提高。

混沌系统具备和传统密码技术不同的应用特征, 适用于图像加密领域。混沌映射图像加密有两种主流方法： 空域加密与变换域加密, 而空域加密速率更快, 计算更简单。为此笔者提出一种基于混沌映射的空域彩色图像复合加密算法。采用深度残差网络消除图像噪声, 运用置乱变换与扩散操作增强图像加密安全性, 凭借Logistic映射实现彩色图像高质量加密目标。

1 空域彩色图像预处理

为进一步明确彩色图像边缘信息, 增强图像加密整体效果, 采用深度残差网络实施图像去噪。传统卷积网络传输数据时, 极易丢失数据[7], 残差网络直接把输入数据传递到输出层, 保护了数据完整性。残差网络结构的非线性层拟合残差为

ψ(x)=A(x)-x

(1)

其中ψ(x)是图像去噪后的输出值,A(x)是包含噪声的彩色图像,x是残差网络训练检测到的噪声数量。

因残差和含噪图像相比会减少较多特征, 使用残差优化计算近似最优的恒等映射[8]时, 会进一步缩短网络训练时长, 去噪性能也得到显著提升。残差去噪网络由4部分构成： 输入输出层、 特征提取层、 残差单元层与网络重构层。将初始彩色图像看作输入值, 输入与输出的图像大小完全相同。特征提取层使用图像块完成网络训练, 把小块样本从图像空间投影至特征空间, 推导图像特征细节信息, 再把此类特征拟作滤波器, 和初始彩色图像进行卷积计算, 获取初始图像随机方位不同特征的激活值。采用Relu激活函数与一个4×4大小的卷积层提取图像块特征, 把神经元传输至残差单元层中。

残差单元层通过若干残差块连接构成[9], 在残差单元块中添加跳跃连接, 提高网络训练收敛速率。将各残差单元块的数学模型记作

BC=D(BC-1)+B2

(2)

其中B是残差单元块,C是单元块数量,D(·)是残差映射函数。

网络重构层是网络的最底层[10], 将输入与输出图像合并为一个低噪图像。为衡量去噪结果可靠性, 使用均方根误差衡量重构后图像与初始彩色图像的差别, 计算公式为

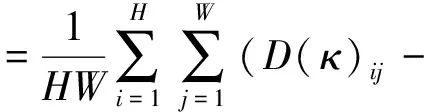
(3)

其中H、W分别是图像高度与宽度, ϑ是输入图像,D(κ)是去噪后的图像,i、j是D(κ)的第i行、 第j列的像素值。

2 混沌映射下空域彩色图像复合加密算法

为提升图像复合加密算法抗噪攻击能力, 融合多普勒波与小波变换法对图像进行置乱计算, 打乱图像像素原有位置[11]。多普勒效应为一种自然现象, 广泛存在于声波、 电磁波等各类波形中, 表示在波源与观测者之间具备相对运动时, 观测者获得的频率和波源不相等的检测结果。

设定波源的频率是f0, 波源运动速率是s, 声音在空气内传播的速率是e, 观察者g和波源运动方位的间距是l, 则观测者接收的频率是

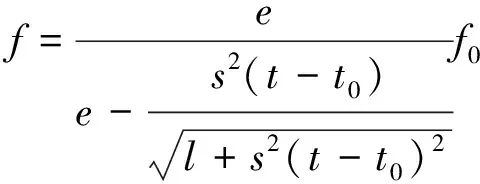
(4)

其中t是观测时间,t0是声源和观测者方位相对的时间中心点； 若tf0, 表明声源与观测者之间的距离较近, 反之二者的间距较远。

小波变换把信号划分成若干个尺度[12], 不同尺度呈现出不同的频域特点, 可有效分析彩色图像的空域特征。因低频子带涵盖了图像的大量隐含信息, 低频系数的改变对图形置乱的成效尤为显著[13-14]。笔者首先对图像进行小波变换, 计算其频域分布, 然后对频率系数实施多普勒像素置乱, 具体过程如下：

1) 若初始彩色图像是h(x,y), 将其变换为灰度图像, 设置图像块大小是b×d, 把图像划分为p×q个不相交的子图像；

2) 小波变换子图像, 使用小波工具箱内的随机小波对子图像实施二维小波分解, 则图像的低频系数为L；

3) 使用式(4)获得多普勒数据E, 在多普勒多项式内, 随机提取若干数值对数据E进行行列变换[15], 完成低频系数与高频系数置乱；

4) 将上述已经置乱的高、 低频系数实施二维小波反向转换, 生成置乱图像F。

利用上述过程完成置乱变换后, 即使像素方位与数值均呈现混乱状态, 但像素之间无任何计算关联, 极易遭受明文攻击[16]。在置乱变换基础上引入扩散操作, 让相同密钥状态下, 每个明文的等效密钥均不相等, 令混沌序列与图像具备充分的耦合关系[17], 优化图像安全性, 扩散操作基本思路如下。

ζ(z)={τ|(τ-z)∈[-ζ,ζ]2}

(5)

ζ(z′)={τ′|(τ′-z′)∈[-ζ,ζ]2}

(6)

其中ζ是近邻区域的半径,τ是像素点个数。将满足二维视差梯度约束条件的候选匹配集合定义为

ζ(z,z′)={τ∈ζ(z),τ′∈ζ(z′),‖(τ′-z′)-(τ-z)‖∞≤μ}

(7)

其中μ是视差梯度临界值, 一般取值0.5。

把待扩散像素点依照零均值归一化互相关分数排列成一个队列[18], 并依照分数大小从上至下进行划分, 若零均值归一化互相关分数与置信度均超出预设临界值, 且从未被匹配过, 则将其保存并放入队列内, 标记为1, 反之标记为0。置信度的计算公式为

o(τ)=max{|I(τ+1)-I(τ)|}

(8)

其中I是置信度迭代指数。

迭代操作上述步骤直至队列为空, 实现图像扩散处理。

混沌映射是一种非线性动力系统内出现的确定性随机过程, 展现出非周期且不收敛状态。从时域角度观察, 混沌映射获得的序列与随机序列相似, 相关性很弱, 拥有优秀的类白噪声特征, 可生成伪随机信号与伪随机码[19]。只要增多迭代数量, 伪随机码的周期可以变得很长, 在保密通信工作领域得到广泛应用, 是一种新型加密技术。

Logistic映射是混沌映射中最常用的映射方式之一, 将其方程式描述为

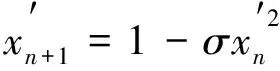
(9)

混沌系统生成的序列概率分布函数是

(10)

其中π是概率常数。

(11)

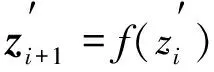
(12)

(13)

3 仿真实验

使用Matlab 7.0平台进行图像加密实验, 使用大小为256×256 像素的Lena彩色图片。一个优秀的算法应当抵御全部的已知攻击类型, 譬如选择明文攻击、 统计攻击等, 下面从不同角度对笔者方法进行安全性评估。

3.1 加密随机性检测

采用随机数检测标准NIST SP 800-22数据集验证笔者方法加密后的图像随机性, 检测结果和接收水平M有直接关系。若M=1, 证明测试序列呈现完全随机状态； 若M=0, 表明测试序列没有表现出随机状态。通常情况下,M值高于0.3就认定序列具备随机状态。为便于实施随机性检测, 从加密后的图像内任意挑选1 354 000位的二进制序列, 检测结果如表1所示。

从表1可知, 各项检测结果的接收水平均大于0.3, 笔者方法成功通过了随机数检测标准检测, 证明使用该方法加密彩色图像后, 密文呈现随机分布趋势, 攻击者很难从图像中发现破解规律, 有效提升图像加密的安全性能。

表1 密文图像随机性检测

3.2 直方图分析

直方图展现出图像灰度级和其自身出现频率之间的特征关系, 图像的直方图平滑性越好, 加密效果越优。图1依次为Lena图像明文与密文的红(R)、 绿(G)、 蓝(B)颜色分量的直方图。

从图1可知, 在不同的颜色分量中, 明文图像直方图分布具备显著的像素特征, 极易遭受恶意攻击, 密文图像直方图的分布更加匀称。由此看出, 笔者加密方法能很好地掩盖明文图像内的像素特征, 让攻击者无法提取有用数据发动统计攻击, 具备极强的抗攻击能力。

图1 明文与密文图像的颜色分量直方图Fig.1 Color component histogram of plain text and cipher text images

3.3 信息熵特征

信息熵用于衡量图像内灰度值的分布状态, 灰度分布越均匀, 信息熵值越高, 图像加密稳定性越好。一幅256级的灰度图像期望信息熵是8, 若小于8, 表明大概率会遭受攻击威胁, 若接近期望值8, 证明信息的遗漏可忽略不计, 加密算法具备充足的安全等级。信息源q的信息熵推导解析式为

(14)

图2 3种方法信息熵值对比Fig.2 Comparison of information entropy of three methods

其中R′(qi)是像素qi出现的概率, 2n是初始图像像素灰度等级。

将笔者方法与文献[5]傅里叶变换法、 文献[6]魔方密码法进行仿真对比, 3种方法加密后的信息熵结果如图2所示。

观察图2可知, 笔者方法得到的密文图像信息熵值最接近理想值, 表明密文图像像素值分布的随机性较强, 泄露图像重要信息的概率极低, 与上述实验结论相吻合, 综合判断笔者方法在彩色图像加密中拥有极大优势, 实用性更高。

4 结 语

为增强图像加密算法安全性, 提出一种基于混沌映射的空域彩色图像复合加密算法。笔者方法可操作性强、 计算简便, 能改变图像像素值位置与大小, 保密性得到显著提高。仿真实验结果证实, 所提方法加密视觉效果良好, 密钥敏感性强, 有效抵抗了选择明文攻击。在以下研究中,将在算法内融入更高维的混沌系统, 生成三维类仿射变换参数, 优化像素位置的随机性。

参考文献：

[1]邓小鸿, 梁涤青, 刘惠文. 基于2D sine logistic混沌映射的医学图像频域加密算法 [J]. 计算机应用研究, 2020, 37(2): 530-534.

DENG Xiaohong, LIANG Diqing, LIU Huiwen. Medical Image Encryption Algorithm in Frequency Domain Base on 2D Sine Logistic Chaotic Mapping [J]. Application Research of Computers, 2020, 37(2): 530-534.

[2]PATRO K, ACHARYA B. An Efficient Dual-Layer Cross-Coupled Chaotic Map Security-Based Multi-Image Encryption System [J]. Nonlinear Dynamics, 2021, 104(3): 2759-2805.

[3]BALASKA N, AHMIDA Z, BELMEGUENAI A, et al. Image Encryption Using a Combination of Grain-128a Algorithm and Zaslavsky Chaotic Map [J]. IET Image Processing, 2020, 14(6): 1120-1131.

[4]班多晗, 吕鑫, 王鑫元. 基于一维混沌映射的高效图像加密算法 [J]. 计算机科学, 2020, 47(4): 278-284.

BAN Duohan, LÜ Xin, WANG Xinyuan. Efficient Image Encryption Algorithm Based on 1D Chaotic Map [J]. Computer Science, 2020, 47(4): 278-284.

[5]史进, 蔡竞, 徐锋. 傅里叶变换耦合DNA编码的图像加密算法 [J]. 计算机工程与设计, 2021, 42(7): 1874-1881.

SHI Jin, CAI Jing, XU Feng. Image Encryption Algorithm Based on Fourier Transform and DNA Coding [J]. Computer Engineering and Design, 2021, 42(7): 1874-1881.

[6]孙光民, 王皓. 基于魔方密码的图像加密解密技术 [J]. 北京工业大学学报, 2021, 47(8): 833-841.

SUN Guangmin, WANG Hao. Image Encryption and Decryption Technology Based on Rubik’s Cube and Dynamic Password [J]. Journal of Beijing University of Technology, 2021, 47(8): 833-841.

[7]陈波, 鄢爱兰. 改进型多项式匹配图像去噪算法的研究与应用 [J]. 电子测量与仪器学报, 2021, 35(4): 177-186.

CHEN Bo, YAN Ailan. Application and Research of Improving Polynomial Fitting Algorithms for Images Denoising [J]. Journal of Electronic Measurement and Instrumentation, 2021, 35(4): 177-186.

[8]ZHANG Y Q, HAO J L, WANG X Y. An Efficient Image Encryption Scheme Based on S-Boxes and Fractional-Order Differential Logistic Map [J]. IEEE Access, 2020, 8(99): 54175-54188.

[9]王文豪, 严云洋, 姜明新, 等. 基于噪声检测和动态窗口的图像去噪算法 [J]. 图学学报, 2019, 40(1): 111-116.

WANG Wenhao, YAN Yunyang, JIANG Mingxin, et al. Image Denoising Algorithm Based on Noise Detection and Dynamic Window [J]. Journal of Graphics, 2019, 40(1): 111-116.

[10]XIE D, CHEN F, LUO Y, et al. One-to-Many Image Encryption with Privacy-Preserving Homomorphic Outsourced Decryption Based on Compressed Sensing [J]. Digital Signal Processing, 2019, 95(5): 102587.

[11]高成明, 黄欣, 唐薪玥, 等. 基于混沌的置乱-扩散图像加密算法 [J]. 黑龙江大学自然科学学报, 2019, 36(3): 363-370.

GAO Chengming, HUANG Xin, TANG Xinyue, et al. Chaos-Based Scrambling-Diffusion Image Encryption Algorithm [J]. Journal of Natural Science of Heilongjiang University, 2019, 36(3): 363-370.

[12]SHEN Q, LIU W, LIN Y, et al. Designing an Image Encryption Scheme Based on Compressive Sensing and Non-Uniform Quantization for Wireless Visual Sensor Networks [J]. Sensors, 2019, 19(14): 20.

[13]李蓝航, 丘森辉, 肖丁维, 等. 基于DNA序列和动态索引扩散的图像加密算法 [J]. 广西师范大学学报(自然科学版), 2021, 39(3): 40-53.

LI Lanhang, QIU Senhui, XIAO Dingwei, et al. Image Encryption Algorithm Based on DNA Sequence and Dynamic Index Diffusion [J]. Journal of Guangxi Normal University (Natural Science Edition), 2021, 39(3): 40-53.

[14]LI C, LUO G, LI C. An Image Encryption Scheme Based on the Three-Dimensional Chaotic Logistic Map [J]. International Journal of Network Security, 2019, 21(1): 22-29.

[15]黄迎久, 杜永兴, 石炜. 基于新的组合混沌映射的图像加密算法 [J]. 微电子学与计算机, 2019, 36(5): 47-52.

HUANG Yingjiu, DU Yongxing, SHI Wei. Image Encryption Algorithm Based on a Novel Combinatorial Chaotic Mapping [J]. Microelectronics & Computer, 2019, 36(5): 47-52.

[16]ZHU H H, CHEN X B, YANG Y X. A Quantum Image Dual-Scrambling Encryption Scheme Based on Random Permutation [J]. Science China Information Sciences, 2019, 62(12): 1-3.

[17]CHNE L P, YIN H, YUAN L G, et al. A Novel Color Image Encryption Algorithm Based on a Fractional-Order Discrete Chaotic Neural Network and DNA Sequence Operations [J]. Frontiers of Information Technology & Electronic Engineering, 2020, 21(6): 866-879.

[18]ROY M, CHAKRABORTY S, MALI K, et al. A Robust Image Encryption Framework Based on DNA Computing and Chaotic Environment [J]. Microsystem Technologies, 2021, 27(10): 3617-3627.

[19]张健, 陈楠楠, 李妍. 基于混沌映射与动态S盒的图像加密算法 [J]. 中国电子科学研究院学报, 2019, 14(11): 1129-1135.

ZHANG Jian, CHEN Nannan, LI Yan. Image Encryption Algorithm Based on Chaotic Map and Dynamic S-Box [J]. Journal of China Academy of Electronics and Information Technology, 2019, 14(11): 1129-1135.

[20]WANG X, ZHAO H, HOU Y, et al. Chaotic Image Encryption Algorithm Based on Pseudo-Random Bit Sequence and DNA Plane [J]. Modern Physics Letters B, 2019, 33(22): 1950263.