Algorithmic Correspondence Theory for Sabotage Modal Logic*

Zhiguang Zhao

Abstract.Sabotage modal logic (SML) is a kind of dynamic logic.It extends static modal logic with a dynamic modality which is interpreted as “after deleting an arrow in the frame,the formula is true”.In the present paper,we are aiming at solving an open problem stated in Aucher,van Benthem and Grossi(2018),namely giving a Sahlqvist-type correspondence theorem (Sahlqvist 1975) for sabotage modal logic.In this paper,we define sabotage Sahlqvist formulas and give an algorithm ALBASML to compute the first-order correspondents of sabotage Sahlqvist formulas.We give some remarks and future directions at the end of the paper.

1 Introduction

Sabotage modal logic(SML,[6])belongs to the class of logics collectively called dynamic logics.It extends static modal logic with a dynamic modality ♦such that♦φis interpreted as“after deleting an arrow in the frame,φis true”.There are several existing works on sabotage modal logic.In[5],a bisimulation characterization theorem as well as a tableau system were given for sabotage modal logic,[13]proved the undecidability of the satisfiability problem and gave the complexity of the modelchecking problem,and[14]gave the complexity of solving sabotage game.Several similar formalisms are also investigated,such as graph modifiers logic ([4]),swap logic([1])and arrow update logic([11]),modal logic of definable link deletion([12]),modal logic of stepwise removal([17]).These logics are collectively called relation changing modal logics.([2,3])In the present paper,we are aiming at solving an open problem stated in[5],namely giving a Sahlqvist-type correspondence theorem([16])for sabotage modal logic.We define the Sahlqvist formulas in the sabotage modal language and give the sabotage counterpart of the algorithm ALBASML(Ackermann Lemma Based Algorithm),which is sound over Kripke frames and is successful on sabotage Sahlqvist formulas,to show that every Sahlqvist formula in the sabotage modal language has a first-order correspondent.

The structure of the paper is as follows: in Section 2,we give a brief sketch on the preliminaries of sabotage modal logic,including its syntax,semantics as well as the standard translation.In Section 3–8 we define sabotage Sahlqvist formulas and the algorithm ALBASML,show its soundness over Kripke frames and its success on sabotage Sahlqvist inequalities.In Section 9 we give some further directions.

2 Preliminaries on Sabotage Modal Logic

In this section,we collect some preliminaries on sabotage modal logic.For further details,see[5].

Given a set Prop of propositional variables,the set of sabotage modal formulas is recursively defined as follows:

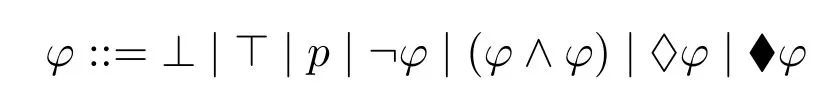
wherep ∈Prop,♢is the alethic connective of ordinary modal logic and ♦is the sabotage connective of sabotage modal logic.We will follow the standard rules for omission of the parentheses.∨,→,↔,□,■can be defined in the standard way.We call a formulastaticif it does not contain ♦or ■.An occurence ofpis said to bepositive(resp.negative) inφifpis under the scope of an even (resp.odd) number of negations in the original sabotage modal language.A formulaφis positive(resp.negative)if all occurences of propositional variables inφare positive(resp.negative).

For the semantics of sabotage modal logic,we use Kripke frames F=(W,R)and Kripke models M=(F,V)whereV:Prop→P(W).The satisfaction relation is defined as follows:

Intuitively,♦φis true atwiff there is an edge (w0,w1) ofRsuch that after deleting this edge fromR,the formulaφis still true atw.It is easy to see that the semantic clause for ■is defined as follows:

(W,R,V),w⊩■φiff for all edges(w0,w1)∈R,(W,R{(w0,w1)},V),w⊩φ.

The standard translation of sabotage modal language into first-order logic is given as follows (notice that we need to record the edges already deleted fromRso that we know what edges could still be deleted):

Definition 1([5,Def.1]).LetEbe a set of pairs (y,z) of variables standing for edges and letxbe a designated variable.The translationis recursively defined as follows:

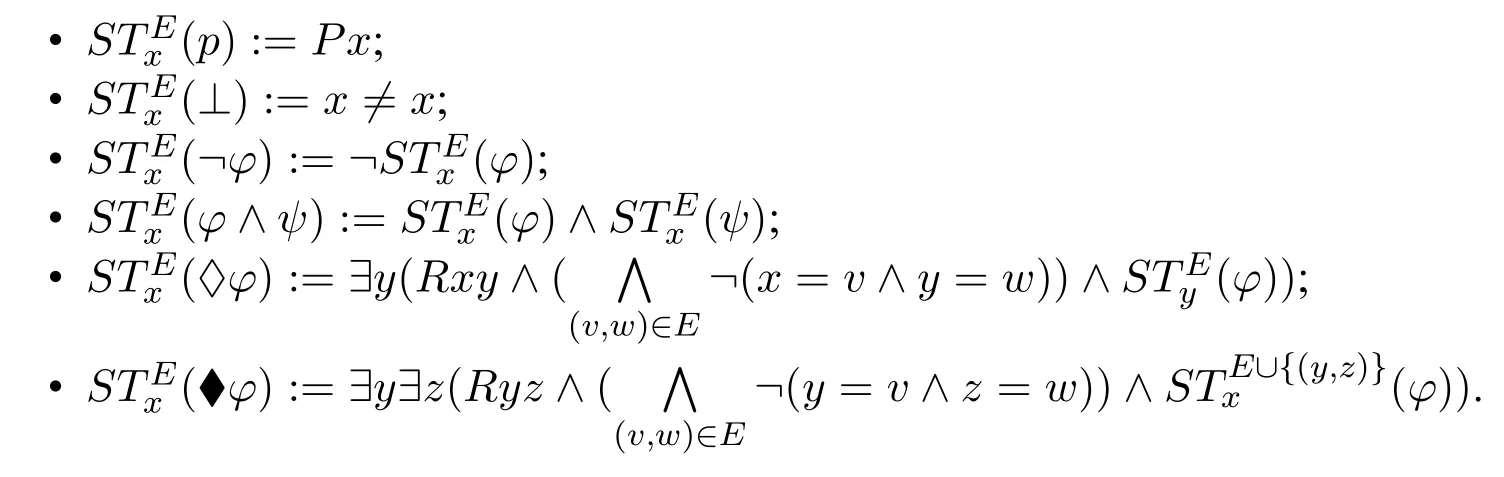
It is proved in[5,Thm.1]that this translation is correct:

Theorem 1.For any pointed model(M,w)and sabotage modal formula φ,

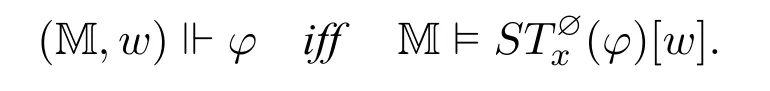
3 Algorithmic Correspondence for Sabotage Modal Logic: A Sketch

We will develop the correspondence algorithm ALBASMLfor sabotage modal logic,in the style of[8,9].The basic idea is to use an algorithm ALBASMLto transform the modal formulaφ(→p)into an equivalent set of pure quasi-(universally quantified)inequalities which does not contain occurrences of propositional variables,and therefore can be translated into the first-order correspondence language via the standard translation of the expanded language of sabotage modal logic (which will be defined on Section 4).

The key ingredients of the algorithmic correspondence proof can be listed as follows:

· An expanded sabotage modal language as the syntax of the algorithm,as well as their interpretations in the relational semantics；

· An algorithm ALBA which transforms a given sabotage modal formulaφ(→p)into equivalent pure quasi-(universally quantified)inequalities Pure(φ(→p))；

· A soundness proof of the algorithm；

· A syntactically identified class of formulas on which the algorithm is successful；

· A first-order correspondence language and first-order translation which transform pure quasi-(universally quantified)inequalities into their equivalent firstorder correspondents.

In the remainder of the paper,we will define an expanded sabotage modal language which the algorithm will manipulate(Section 4.1),define the first-order correspondence language of the expanded sabotage modal language and the standard translation(Section 4.2).We report on the definition of Sahlqvist inequalities(Section 5),define a modified version of the algorithm ALBASML(Section 6),and show its soundness(Section 7)and success on Sahlqvist inequalities(Section 8).

4 The Expanded Language in the Algorithm

4.1 The expanded sabotage modal language

In the present subsection,we give the definition of the expanded sabotage modal languageand its standard translations,which will be used in the execution of the algorithm:

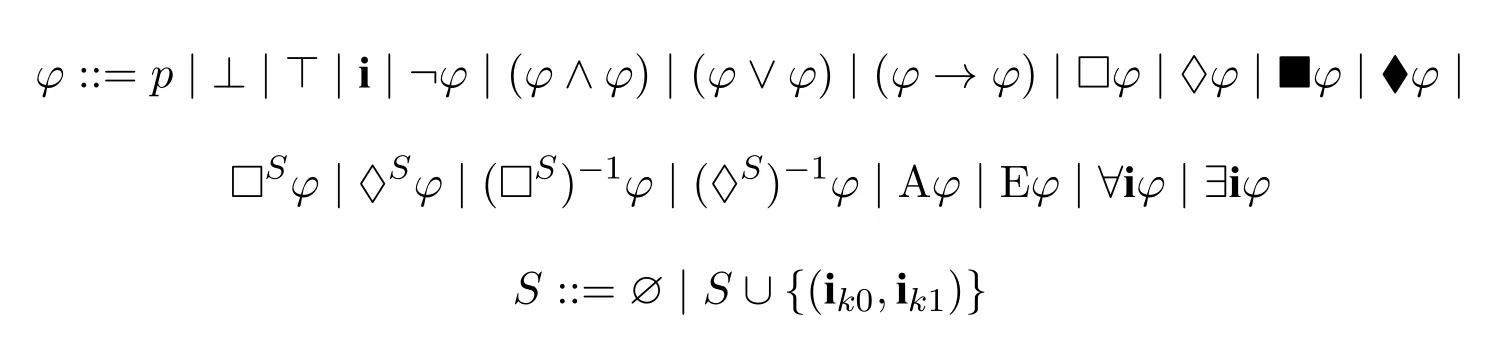
where i is called nominal as in hybrid logic([7,Ch.14]),ik0,ik1are fresh nominals not inS.We use the notationto indicate that the propositional variables occurring inφare all inWe call a formulapureif it does not contain propositional variables.

When interpreting the formulas in the expanded language,we assume that we start from a given pointed model ((W,R0,V),w),and useSto record the edges deleted fromR0.□S,♢Scorrespond to the relationR0{(V(ik0),V(ik1))|(ik0,ik1)∈S}(denoted asR0S),(□S)-1,(♢S)-1correspond to the relationV(ik0))|(ik0,ik1)∈S}(denoted as(R0S)-1),which intuitively means first delete the edges in S and then take the inverse relation.Unlabelled □and ♢correspond to the relationRafter certain deletions of edges.Therefore,we can say that □S,♢S,(□S)-1,(♢S)-1are“absolute connectives”whose interpretations just depend onR0andS,while □and ♢are“contextual connectives”whose interpretations depend on the concreteRafter certain steps of deletions.For ■and ♦,their interpretations depend on the context.A and E are global box and diamond modalities respectively,(W,R,V),w⊩∀iφindicates that for all valuation variantsuch thatis the same asVexcept that,w⊩φ,and (W,R,V),w⊩∃iφis the corresponding existential statement.

For the semantics of the expanded sabotage modal language,the valuation is defined asV:Prop∪Nom→P(W)similar to hybrid logic,and for the modal and dynamic connectives,the additional semantic clauses can be given as follows(notice that hereRis the “actual” accessibility relation in the model M=(W,R,V) after some(maybe none)edges have been deleted,whileR0is the“starting accessibility”relation when no edge has been deleted yet,andR0Sis the notation forR0{(V(ik0),V(ik1))|(ik0,ik1)∈S}):

Here we do not require that each pair of nominals inSdenote different edges inR0.For the convenience of the algorithm,we introduce the following definitions:

Definition 2.

· Aninequalityis of the formψ,whereφandψare formulas,SandS′record the context ofφandψrespectively,i.e.which edges have already been deleted.Its interpretation is given as follows:

· AMega-inequalityis defined inductively as follows:

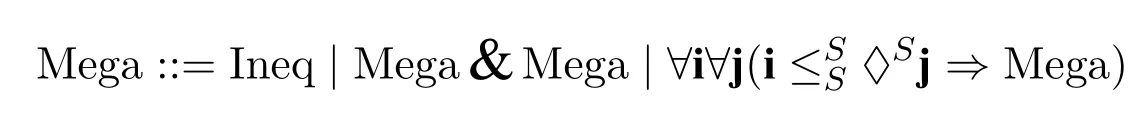
where Ineq is an inequality,&is the meta-conjunction and⇒is the metaimplication.Its interpretation is given as follows:

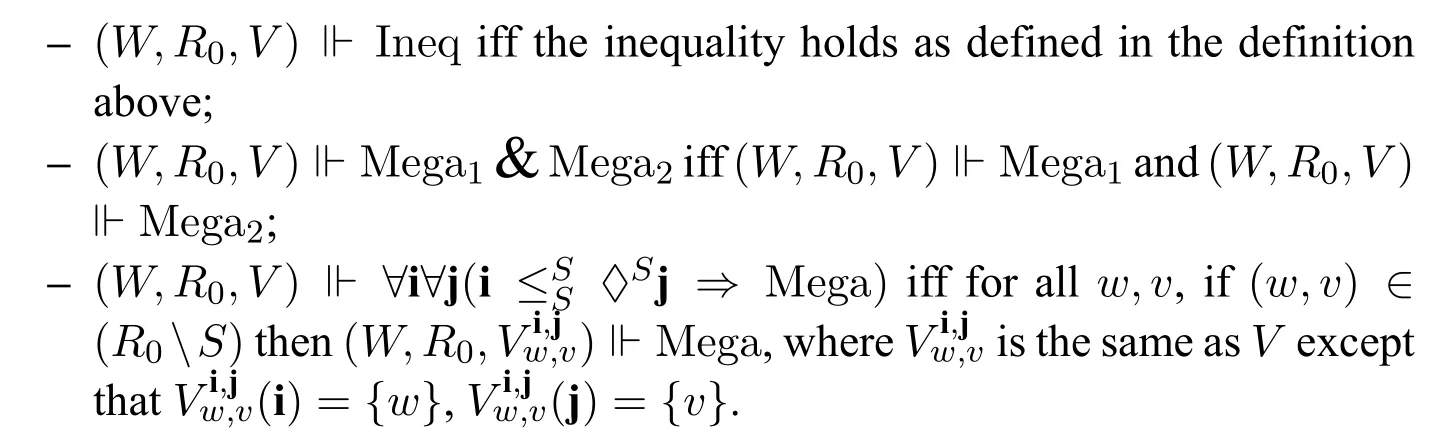
· Auniversally quantified inequalityis defined as,and its interpretation is given as follows:

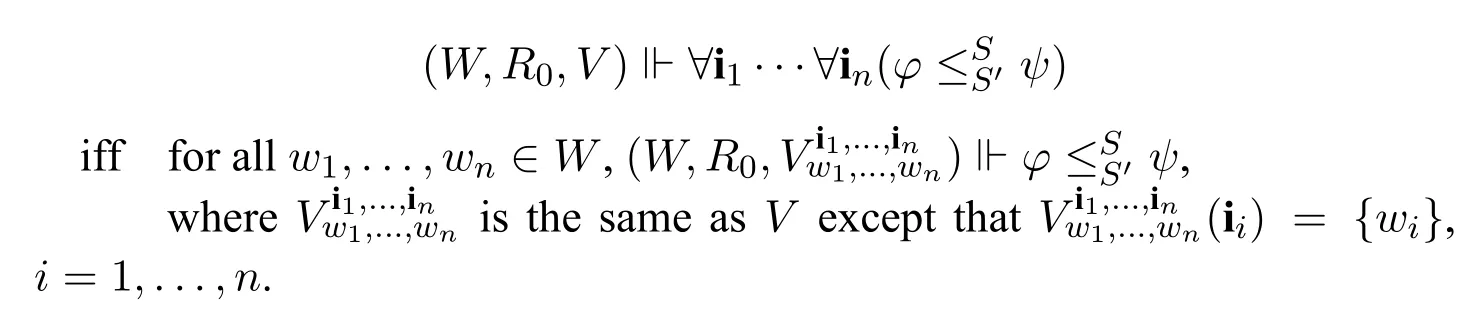
· Aquasi-universally quantified inequalityis defined as UQIneq1&···&UQIneqn⇒UQIneq where UQIneq,UQIneqiare universally quantified inequalities.Its interpretation is given as follows:

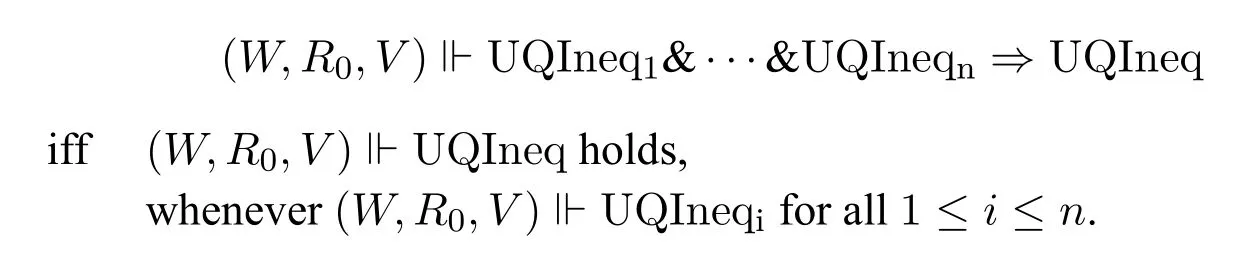
For inequalities,we have the following properties,which will be useful in the soundness proofs:

Proposition 2.

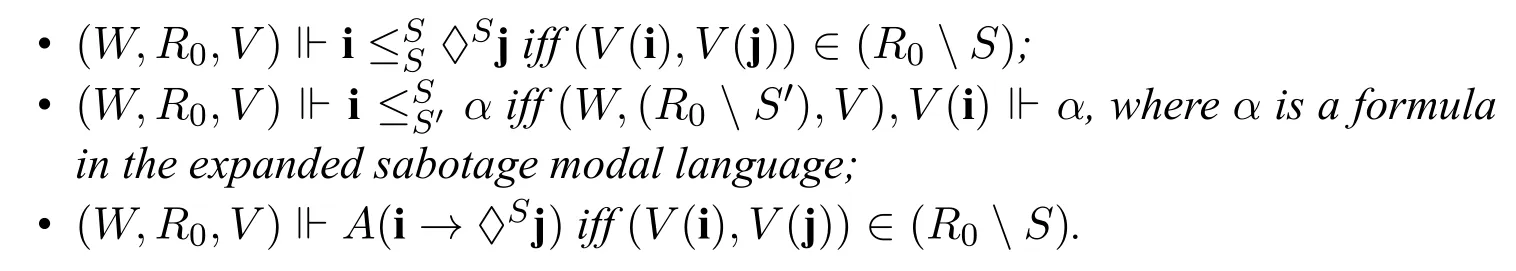
4.2 The first-order correspondence language and the standard translation

In the first-order correspondence language,we have a binary relation symbolRcorresponding to the binary relation,a set of constant symbolsicorresponding to each nominal i,a set of unary predicate symbolsPcorresponding to each propositional variablep.

The standard translation of the expanded sabotage modal language is defined as follows:

Definition 3.LetEbe a finite set of pairs(y,z)of variables standing for edges and letxbe a designated variable.The translationis recursively defined as follows:

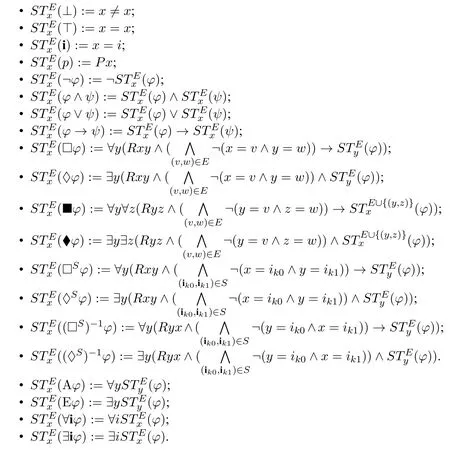
It is easy to see that this translation is correct:

Proposition 3.For any pointed model(M,w)and sabotage modal formula φ,

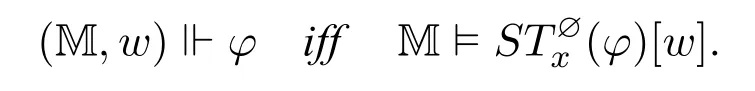
For inequalities,quasi-inequalities,mega-inequalities,universally quantified inequalities and quasi-universally quantified inequalities,the standard translation is given in a global way:

Definition 4.

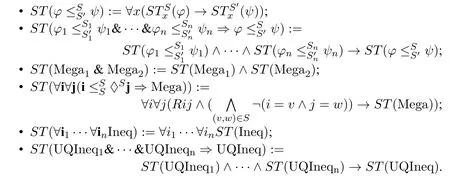
Proposition 4.For any modelMand inequalityIneq,quasi-inequalityQuasi,megainequalityMega,universally quantified inequalityUQIneq,quasi-universally quantified inequalityQUQIneq,

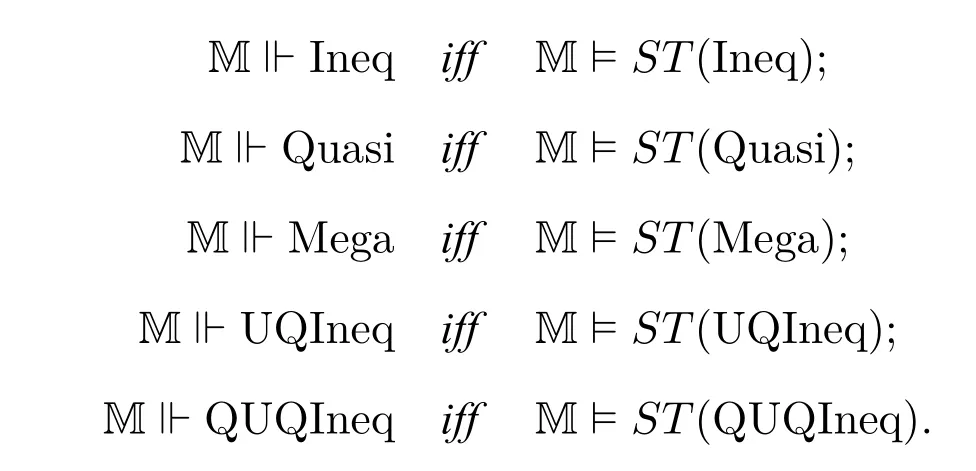
5 Sahlqvist Inequalities

In the present section,since we will use the algorithm ALBASMLwhich is based on the classsification of nodes in the signed generation trees of sabotage modal formulas,we will use the unified correspondence style definition ([10,15]) to define Sahlqvist inequalities.We will collect all the necessary preliminaries on Sahlqvist formulas/inequalities.

Definition 5(Order-type of propositional variables,[9,p.346]).For ann-tuple(p1,...,pn)of propositional variables,an order-typeεof(p1,...,pn)is an element in{1,∂}n.In the order-typeε,we say thatpihas order-type 1 ifεi=1,and denoteε(pi)=1 orε(i)=1；we say thatpihas order-type∂ifεi=∂,and denoteε(pi)=∂orε(i)=∂.

Definition 6(Signed generation tree,[10,Def.4]).Thepositive(resp.negative)generation treeof any given formulaφis defined by first labelling the root of the generation tree ofφwith+(resp.-)and then labelling the children nodes as follows:

· Assign the same sign to the children nodes of any node labelled with∨,∧,□,♢,■,♦,□S,♢S,(□S)-1,(♢S)-1,A,E,∀i,∃i；

· Assign the opposite sign to the child node of any node labelled with¬；

· Assign the opposite sign to the first child node and the same sign to the second child node of any node labelled with→.

Nodes in signed generation trees arepositive(resp.negative) if they are signed +(resp.-).

Example 1.The positive generation tree of+♦(p∧¬■q)→□qis given in Figure 1.

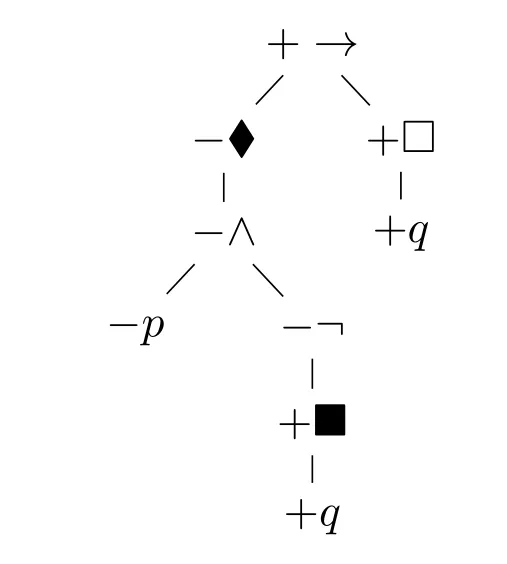
Figure 1 : Positive generation tree for ♦(p ∧¬■q)→□q

Signed generation trees will be used in the inequalitiesφ ≤ψ,where the positive generation tree+φand the negative generation tree-ψwill be considered.We will also say that an inequalityφ ≤ψisuniformin a variablepiif all occurrences ofpiin+φand-ψhave the same sign,and thatφ ≤ψisε-uniformin an arrayifφ ≤ψis uniform inpi,occurring with the sign indicated byε(i.e.,pihas the sign+ifε(pi)=1,and has the sign-ifε(pi)=∂),for each propositional variablepiin

For any given formulaφ(p1,...,pn),any order-typeεovern,and any 1≤i ≤n,anε-critical nodein a signed generation tree*φ(where* ∈{+,-}) is a leaf node +piwhenεi=1 or-piwhenεi=∂.Anε-critical branchin a signed generation tree is a branch from anε-critical node.Theε-critical occurrences are intended to be those which the algorithm ALBASMLwill solve for.We say that+φ(resp.-φ)agrees with ε,and writeε(+φ) (resp.ε(-φ)),if every leaf node in the signed generation tree of+φ(resp.-φ)isε-critical.

We will also use the notation +ψ ≺*φ(resp.-ψ ≺*φ) to indicate that an occurence of a subformulaψinherits the positive(resp.negative)sign from the signedgeneration tree*φ,where* ∈{+,-}.We will writeε(γ)≺*φ(resp.ε∂(γ)≺*φ)to indicate that the signed generation subtreeγ,with the sign inherited from*φ,agrees withε(resp.withε∂).We say that a propositional variablepispositive(resp.negative)inφif+p ≺+φ(resp.-p ≺+φ).

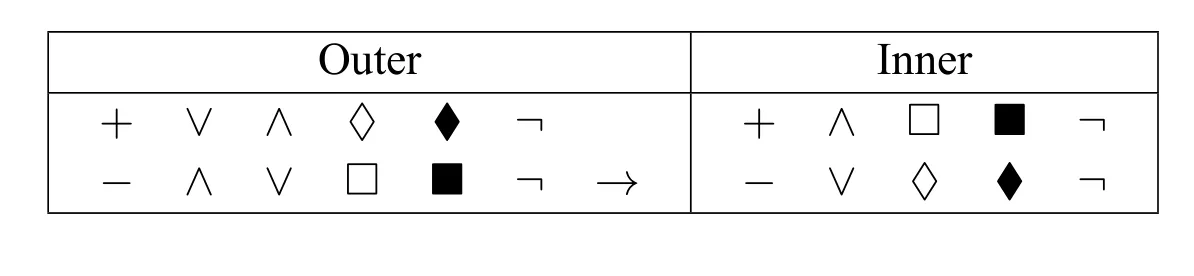
Table 1 : Outer and Inner nodes.

Definition 7([10,Def.5]).Nodes in signed generation trees are calledouter nodesandinner nodes,according to Table 1.

A branch in a signed generation tree is called aexcellent branchif it is the concatenation of two pathsP1andP2,one of which might be of length 0,such thatP1is a path from the leaf consisting(apart from variable nodes)of inner nodes only,andP2consists(apart from variable nodes)of outer nodes only.

Definition 8(Sahlqvist inequalities,[10,Def.6]).For any order-typeε,the signed generation tree*φof a formulaφ(p1,...,pn) isε-Sahlqvistif for all 1≤i ≤n,everyε-critical branch with leafpiis excellent.An inequalityφ ≤ψisε-Sahlqvistif the signed generation trees +φand-ψareε-Sahlqvist.An inequalityφ ≤ψisSahlqvistif it isε-Sahlqvist for someε.

Example 2.Here we give an example of a Sahlqvist inequality for the order-typeε=(1,1),where the outer nodes are marked withO,and the inner nodes are marked withI,andε-critical branches are ended with leaf nodes marked withC.

Figure 2 : (1,1)-Sahlqvist inequality ♦(♢□p1 ∧□(■p1 ∧□p2))≤♢□♢p1 ∨♢□♢p2

6 The Algorithm ALBASML for the Sabotage Modal Language

In the present section,we define the correspondence algorithm ALBASMLfor sabotage modal logic,in the style of[8,9].The algorithm goes in four steps.

1.Preprocessing and first approximation:

In the generation tree of+φand-ψ1The discussion below relies on the definition of signed generation tree in Section 5.In what follows,we identify a formula with its signed generation tree.,

(a) Apply the distribution rules:

i.Push down+♢,+♦,-¬,+∧,-→by distributing them over nodes labelled with+∨which are outer nodes,and

ii.Push down-□,-■,+¬,-∨,-→by distributing them over nodes labelled with-∧which are outer nodes.

(b) Apply the splitting rules:

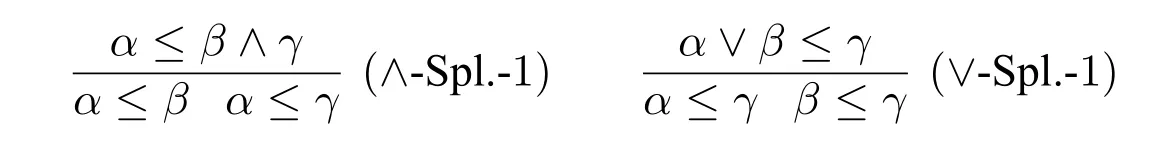
(c) Apply the monotone and antitone variable-elimination rules:

forβ(p)positive inpandα(p)negative inp.

We denote by Preprocess(φ ≤ψ)the finite set{φi ≤ψi}i∈Iof inequalities obtained after the exhaustive application of the previous rules.Then we apply the following rule to every inequality in Preprocess(φ ≤ψ):

Here,i0and i1are special fresh nominals.Now we get a set of inequalities{i0≤φi,ψi ≤¬i1}i∈I.

2.The reduction stage:

In this stage,for each{i0≤φi,ψi ≤¬i1},we first add superscripts and subscripts ∅to the two≤s,and then apply the following rules to prepare for eliminating all the proposition variables in:

(a) Substage 1: decomposing the outer part

In the current substage,the following rules are applied to decompose the outer part of the Sahlqvist signed formula:

i.Splitting rules:

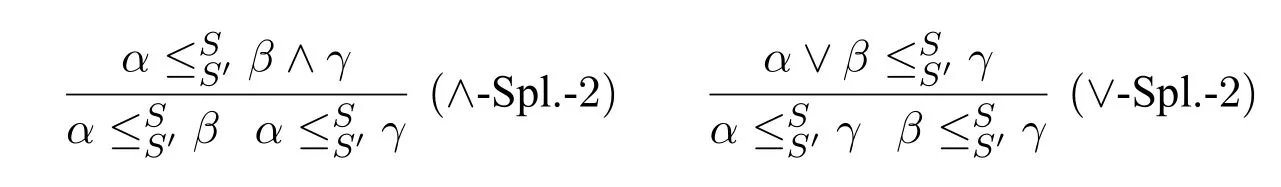
ii.Approximation rules:

The nominals introduced by the approximation rules must not occur

in the system before applying the rule.iii.Residuation rules:

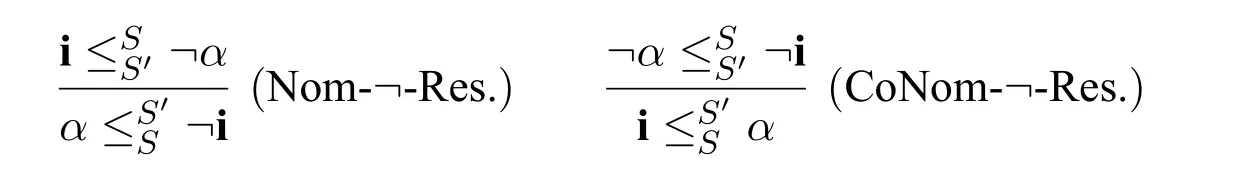
(b) Substage 2: decomposing the inner part

In the current substage,the following rules are applied to decompose the inner part of the Sahlqvist signed formula:

i.Splitting rules:

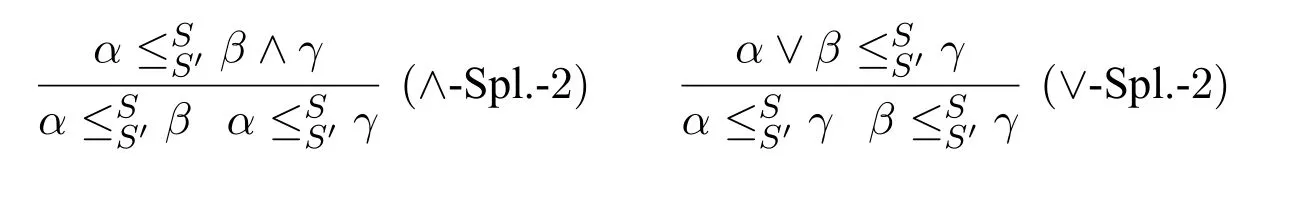
ii.Residuation rules:

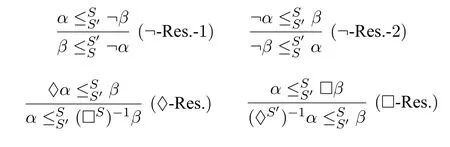
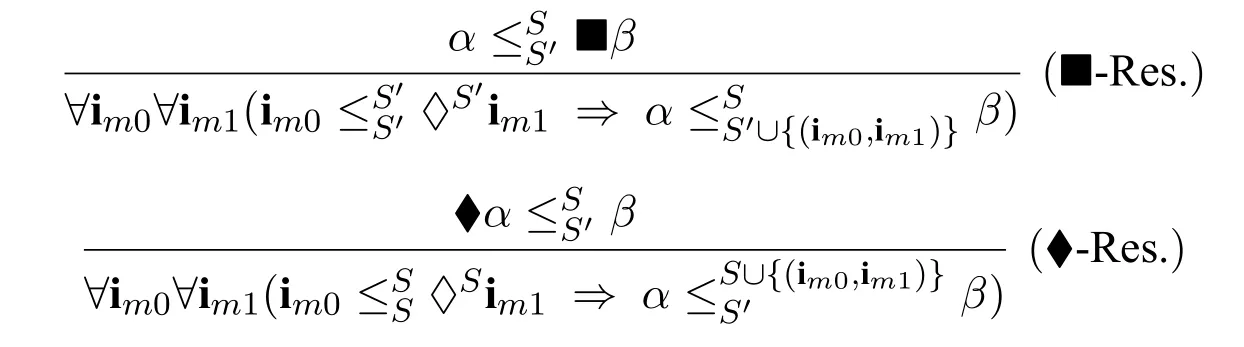
The nominals introduced by the residuation rules must not occur in

the system before applying the rule.iii.Second splitting rules(Second-Spl.):

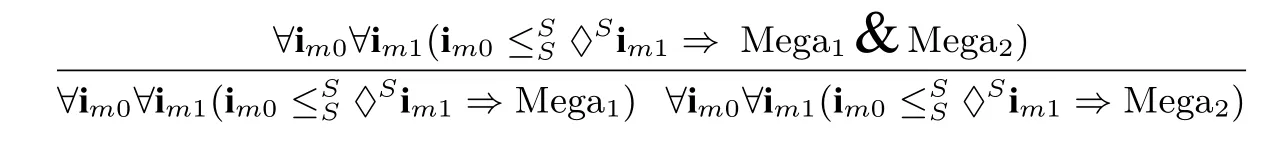
Here Mega1and Mega2denote mega-inequalities.

(c) Substage 3: preparing for the Ackermann rules

In this substage,we prepare for eliminating the propositional variables by the Ackermann rules,with the help of the following packing rules:

Packing rules:

(d) Substage 4: the Ackermann stage

In this substage,we compute the minimal/maximal valuation for propositional variables and use the Ackermann rules to eliminate all the propositional variables.These two rules are the core of ALBA,since their application eliminates proposition variables.In fact,all the preceding steps are aimed at reaching a shape in which the rules can be applied.Notice that an important feature of these rules is that they are executed on the whole set of(universally quantified)inequalities,and not on a single inequality.

3.Output: If in the previous stage,for some{i0≤φi,ψi ≤¬i1},the algorithm gets stuck,i.e.some proposition variables cannot be eliminated by the application of the reduction rules,then the algorithm halts and output “failure”.Otherwise,each initial tuple{i0≤φi,ψi ≤¬i1}of inequalities after the first approximation has been reduced to a set of pure (universally quantified) inequalities Reduce(φi ≤ψi),and then the output is a set of quasi-(universally quantified)inequalities{&Reduce(φi ≤ψi)⇒i0≤¬i1:φi ≤ψi ∈Preprocess(φ ≤ψ)},where &is the big meta-conjunction in quasiinequalities.Then the algorithm use the standard translation to transform the quasi-(universally quantified)inequalities into first-order formulas.

7 Soundness of ALBASML

In the present section,we will prove the soundness of the algorithm ALBASMLwith respect to Kripke frames.The basic proof structure is similar to[9,18].

Theorem 5(Soundness).IfALBASMLruns successfully on φ ≤ψ and outputsFO(φ ≤ψ),then for any Kripke frameF=(W,R0),

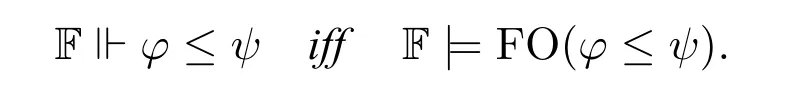
Proof.The proof goes similarly to[9,Thm.8.1].Letφi ≤ψi,1≤i ≤ndenote the inequalities produced by preprocessingφ ≤ψafter Stage 1,and{i0≤φi,ψi ≤¬i1}denote the inequalities after the first-approximation rule,Reduce(φi ≤ψi) denote the set of pure (universally quantified) inequalities after Stage 2,and FO(φ ≤ψ)denote the standard translation of the quasi-(universally quantified)inequalities into first-order formulas,then we have the following chain of equivalences:

It suffices to show the equivalence from(1)to(5)given below:

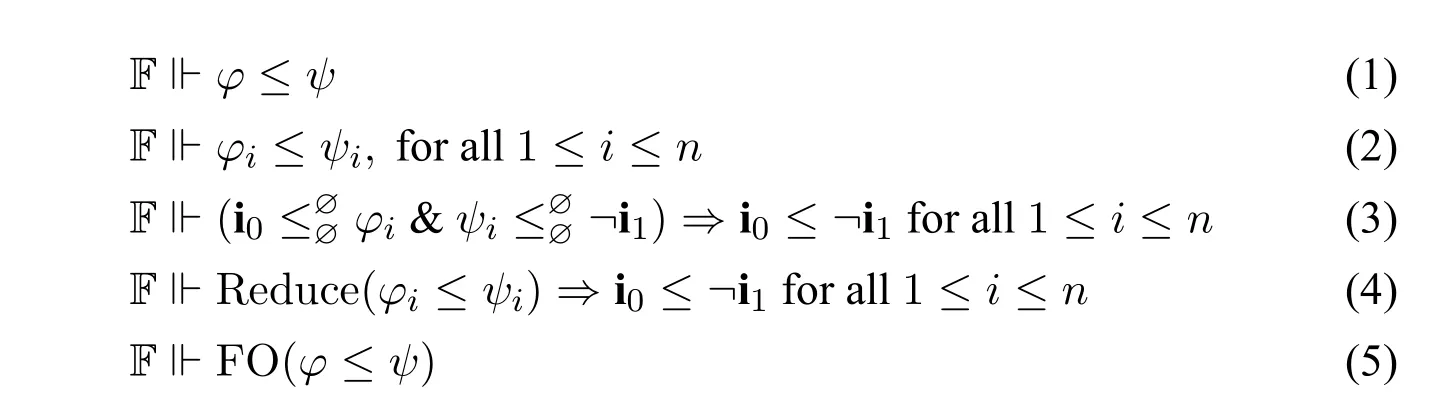
· The equivalence between(1)and(2)follows from Proposition 6；

· the equivalence between(2)and(3)follows from Proposition 7；

· the equivalence between(3)and(4)follows from Propositions 8,9,10,11；

· the equivalence between(4)and(5)follows from Proposition 4. □

In the remainder of this subsection,we prove the soundness of the rules in Stage 1,2 and 3.

Proposition 6(Soundness of the rules in Stage 1).For the distribution rules,the splitting rules and the monotone and antitone variable-elimination rules,they are sound in both directions inF,i.e.,it is sound from the premise to the conclusion and the other way round.

Proof.For the soundness of the distribution rules,it follows from the fact that the following equivalences are valid in F:

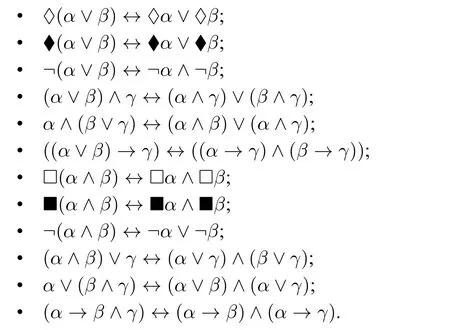
For the soundness of the splitting rules,it follows from the following fact:

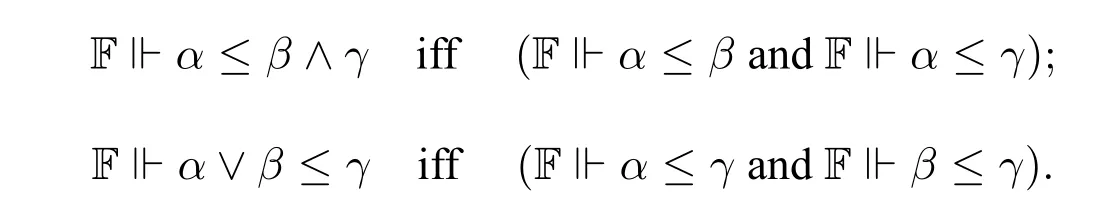
For the soundness of the monotone and antitone variable elimination rules,we show the soundness for the first rule.Supposeα(p)is negative inpandβis positive inp.

If F ⊩α(p)≤β(p),then for all valuationsV,(F,V) ⊩α(p)≤β(p),thus for the valuationsuch thatis the same asVexcept that(p)=∅,(F) ⊩α(p)≤β(p),therefore(F) ⊩α(⊥)≤β(⊥),thus(F,V) ⊩α(⊥)≤β(⊥),so F ⊩α(⊥)≤β(⊥).

For the other direction,suppose F ⊨α(⊥)≤β(⊥),then by the fact thatα(p)is negative inpandβ(p)is positive inp,we have that F ⊨α(p)≤α(⊥)and F ⊨β(⊥)≤β(p),therefore F ⊨α(p)≤β(p).

The soundness of the other rule is similar. □

Proposition 7.(2)and(3)are equivalent,i.e.the first-approximation rule is sound inF.

The next step is to show the soundness of Stage 2,for which it suffices to show the soundness of each rule in each substage.

Proposition 8.The splitting rules,the approximation rules for♢,□,♦,■,→,the residuation rules for¬in Substage 1 are sound inF.

Proof.By Lemma 1,2,3,4 and 5 below. □

Lemma 1.The splitting rules in Substage1and Substage2are sound inF.

Proof.For the soundness of the splitting rules,it follows from the fact that for any Kripke frame F=(W,R0),any valuationVon F,

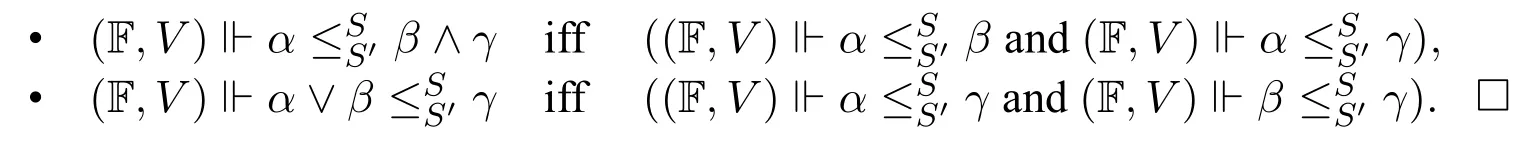
Lemma 2.The approximation rules for♢,□in Substage 1 are sound inF.

Proof.We prove for ♢,the case for □is similar.For the soundness of the approximation rule for ♢,it suffices to show that for any Kripke frame F=(W,R0),any valuationVon F,

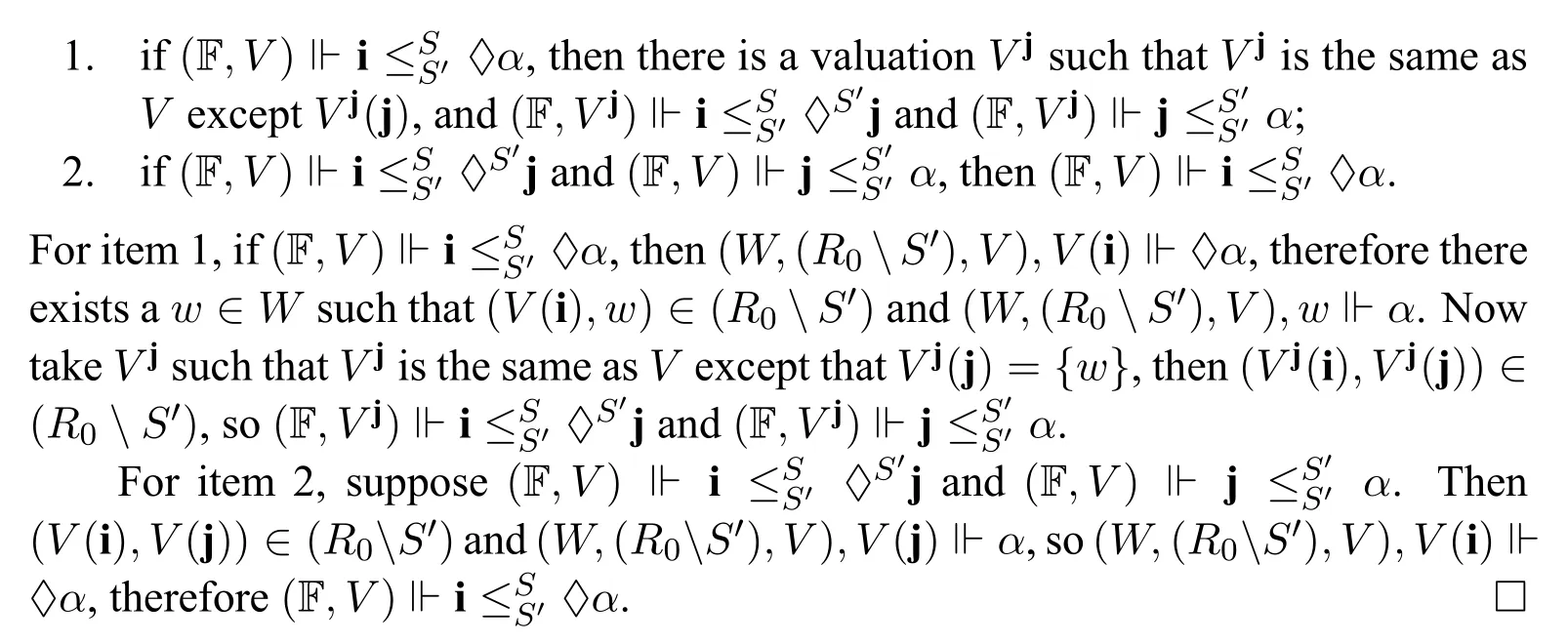
Lemma 3.The approximation rules for♦,■in Substage 1 are sound inF.

Proof.We prove for ♦,the case for ■is similar.For the soundness of the approximation rule for ♦,it suffices to show that for any Kripke frame F=(W,R0),any valuationVon F,

Lemma 4.The approximation rule for →in Substage1is sound inF.

Proof.For the soundness of the approximation rule for→,it suffices to show that for any Kripke frame F=(W,R0),any valuationVon F,

Lemma 5.The residuation rules for¬in Substage1and2are sound inF.

Proof.It is easy to see that the residuation rules for¬in Substage 1 are special cases of the residuation rules for¬in Substage 2 (modulo double negation elimination).Now we only prove it for the residuation rule in Substage 2 where negation symbols occur on the right-hand side of the inequalities,the other rule is similar.

For the soundness of the residuation rule for¬,it suffices to show that for any Kripke frame F=(W,R0),any valuationVon F,(F,V) ⊩iff(F,V) ⊩.Indeed,it follows from the following equivalence:

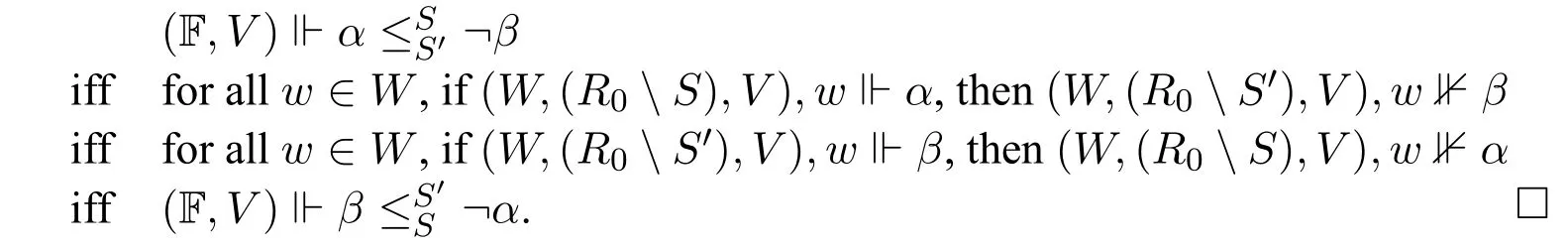
Proposition 9.The splitting rules,the residuation rules for¬,♢,□,♦,■,the second splitting rule in Substage2are sound inF.

Proof.By Lemma 1,5,6,7 and 8. □

Lemma 6.The residuation rules for♢,□in Substage2are sound inF.

Proof.We prove it for ♢,and the rule for □is similar.

Lemma 7.The residuation rules for♦,■in Substage2are sound inF.

Proof.We prove it for ■,and the rule for ♦is similar.

Lemma 8.The second splitting rule in Substage2is sound inF.

Proof.It follows immediately from the meta-equivalence that∀x∀y(α →β∧γ)↔∀x∀y(α →β)∧∀x∀y(α →γ). □

Proposition 10.The packing rules in Substage3are sound inF.

Proof.We only prove the soundness of the first packing rule,the others are similar.

It is easy to see that in the mega-inequality of the premise and in the conclusion,contextual connectives □,♢,■,♦do not occur,so we can ignore the superscripts and subscripts in the inequalities occuring in the rule.

We first define the following mega-inequalities and formulas:

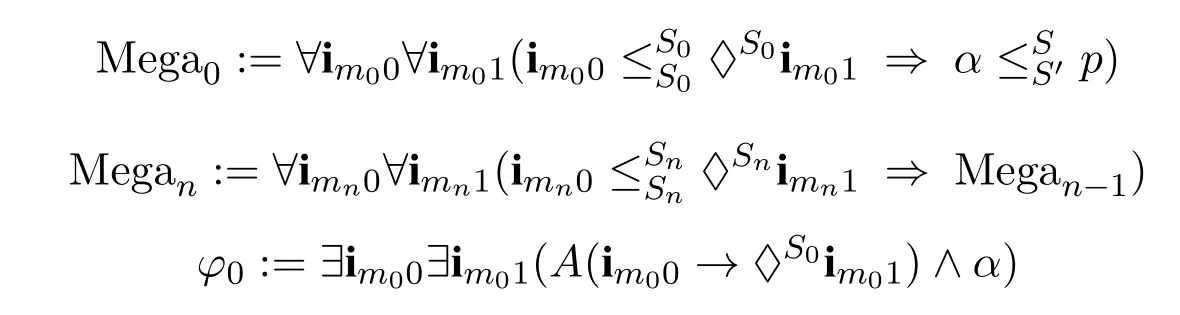
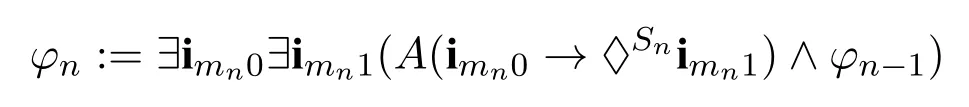
Then we can prove by induction onkthat for any Kripke frame F=(W,R0)and any valuationVon it,

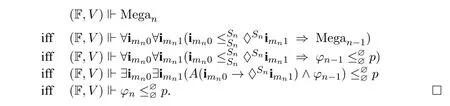
Proposition 11.The Ackermann rules in Substage 4 are sound inF.

Proof.We only prove it for the right-handed Ackermann rule,the other rule is similar.

Without loss of generality we assume thatn=m=1.It suffices to show the following right-handed Ackermann lemma:

Lemma 9.Assume α is pure and contains no contextual modalities□,♢,■,♦and does not contain nominals inβ is positive in p and γ is negative in p,then for any Kripke frameF=(W,R0)and any valuation V on it,

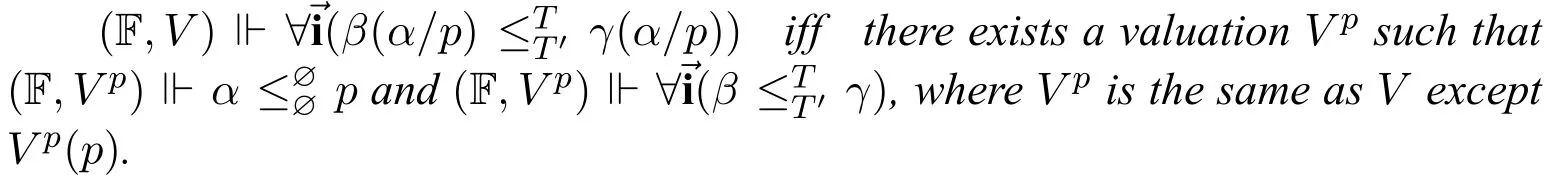
Notice thatαandpdo not contain contextual modalities,so their valuation do not change when the context is different.

⇒: TakeV psuch thatV pis the same asVexcept thatV p(p)=V(α).Sinceαdoes not containp,it is easy to see thatV p(α)=V(α)=V p(p).Therefore(F,V p)⊩.Since the valuation ofαandpdo not change when the context is different,so for anyw ∈W,

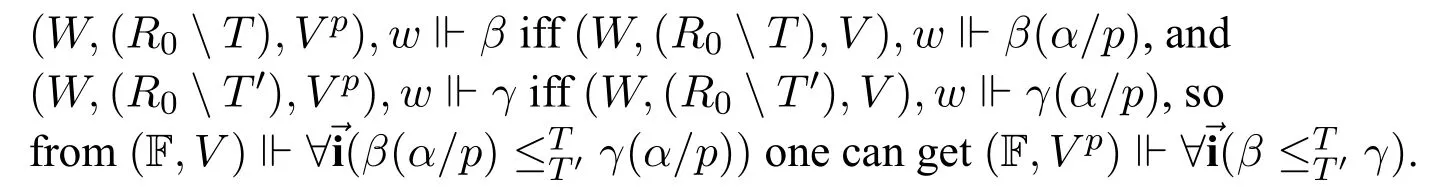
⇐: This direction follows from the monotonicity ofβinpand the antitonicity ofγinp,and that the valuation ofαandpdo not change when the context is different.□

8 Success of ALBASML on Sahlqvist Inequalities

In the present section,we show that ALBASMLsucceeds on all Sahlqvist inequalities,in the style of[18]:

Theorem 12.ALBASMLsucceeds on all Sahlqvist inequalities.

Definition 9(Definiteε-Sahlqvist inequality).Given an order typeε,*∈{-,+},the signed generation tree*φof the termφ(p1,...,pn)isdefinite ε-Sahlqvistif there is no+∨,-∧occurring in the outer part on anε-critical branch.An inequalityφ ≤ψis definiteε-Sahlqvist if the trees+φand-ψare both definiteε-Sahlqvist.

Lemma 10.Let{φi ≤ψi}i∈I=Preprocess(φ ≤ψ)obtained by exhaustive application of the rules in Stage 1 on an input ε-Sahlqvist inequality φ ≤ψ.Then each φi ≤ψi is a definite ε-Sahlqvist inequality.

Proof.It is easy to see that by applying the distribution rules,all occurrences of+∨and-∧in the outer part of anε-critical branch have been pushed up towards the root of the signed generation trees+φand-ψ.Then by exhaustively applying the splitting rules,all such+∨and-∧are eliminated.Since by applying the distribution rules,the splitting rules and the monotone/antitone variable elimination rules do not change theε-Sahlqvistness of a signed generation tree,in Preprocess(φ ≤ψ),each signed generation tree+φiand-ψiareε-Sahlqvist,and since they do not have+∨and-∧in the outer part in theε-critical branches,they are definite. □

Definition 10(Innerε-Sahlqvist signed generation tree).Given an order typeε,* ∈{-,+},the signed generation tree*φof the termφ(p1,...,pn) isinner ε-Sahlqvistif its outer partP2on anε-critical branch is always empty,i.e.itsε-critical branches have inner nodes only.

Lemma 11.Given inequalitiesφi and¬i1obtained from Stage 1 where+φi and-ψi are definite ε-Sahlqvist,by applying the rules in Substage1of Stage2exhaustively,the inequalities that we get are in one of the following forms:

1.pure inequalities which does not have occurrences of propositional variables；

2.inequalities of the formα where+α is inner ε-Sahlqvist；

3.inequalities of the form¬iwhere-β is inner ε-Sahlqvist.

Proof.Indeed,the rules in the Substage 1 of Stage 2 deal with outer nodes in the signed generation trees+φiand-ψiexcept+∨,-∧.For each rule,without loss of generality assume we start with an inequality of the formα,then by applying the rules in Substage 1 of Stage 2,the inequalities we get are either a pure inequality without propositional variables,or an inequality where the left-hand side(resp.righthand side)is i(resp.¬i),and the other side is a formulaα′which is a subformula ofα,such thatα′has one root connective less thanα.Indeed,ifα′is on the left-hand side(resp.right-hand side)then-α′(+α′)is definiteε-Sahlqvist.

By applying the rules in the Substage 1 of Stage 2 exhaustively,we can eliminate all the outer connectives in the critical branches,so for non-pure inequalities,they become of form 2 or form 3. □

Lemma 12.Assume we have an inequalityα or¬iwhere+α and-β are inner ε-Sahlqvist,by applying the rules in Substage2of Stage2,we have(mega-)inequalities(k can be 0 where a mega-inequality becomes an inequality)of the following form:

Notice that for each input inequality,it is of the form¬i,where+αand-βare innerε-Sahlqvist.By applying the splitting rules and the residuation rules in this substage,it is easy to see that the head of the(mega-)inequality will have one side of the inequality pure and have no contextual connectives □,♢,■,♦,and the other side still innerε-Sahlqvist.By applying these rules exhaustively,one will either havepas the non-pure side(with thispon a critical branch),or have an innerε-Sahlqvist signed generation tree with no critical branch,i.e.,ε∂-uniform. □

Lemma 13.Assume we have(mega-)inequalities of the form as described in Lemma12.Then we can get inequalities of the following form:

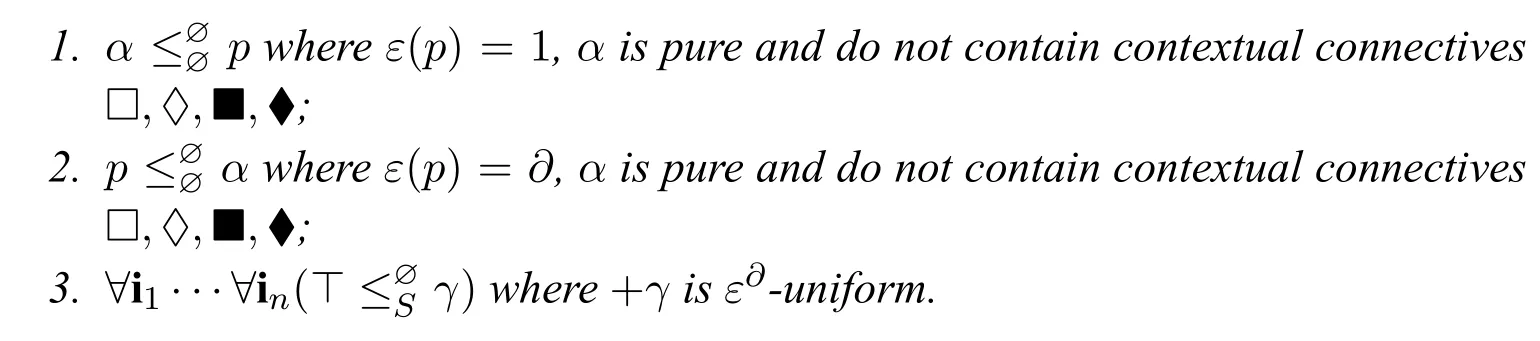
Proof.From the shape of the mega-inequalities,we can see that for all the megainequalities we can apply the corresponding packing rules so that we can get the inequalities as described in the lemma. □

Lemma 14.Assume we have inequalities of the form as described in Lemma13,the Ackermann lemmas are applicable and therefore all propositional variables can be eliminated.

Proof.Immediate observation from the requirements of the Ackermann lemmas.□

Proof of Theorem 12Assume we have anε-Sahlqvist inequalityφ ≤ψas input.By Lemma 10,we get a set of definiteε-Sahlqvist inequalities.Then by Lemma 11,we get inequalities as described in Lemma 11.By Lemma 12,we get the megainequalities as described.Therefore by Lemma 13,we can apply the packing rules to get inequalities and universally quantified inequalities as described in the lemma.Finally by Lemma 14,the(universally quantified)inequalities are in the right shape to apply the Ackermann rules,and thus we can eliminate all the propositional variables and the algorithm succeeds on the input. □

9 Discussions and Further Directions

Future interesting questions include the following:

· Extending the Sahlqvist sabotage formulas to inductive sabotage formulas as well as to the language of sabotage modal logic with fixpoint operators；

· A Kracht-type theorem characterizing the first-order correspondents of Sahlqvist sabotage formulas；

· A Goldblatt-Thomason-type theorem characterizing the sabotage modally definable classes of Kripke frames；

· Extend results on sabotage modal logic to the class of relation changing modal logics.([3])