Indicative Conditionals as Epistemic Filter Conditionals*

Fei Liang Wenfang Wang

Abstract.Deng&Lee(2021)recently give an“extrapolationist”causal-modeling account of the semantics of indicative conditionals.It requires us to have a priority relation on variables and to calculate the induced ordering for submodels,in terms of which the set of minimally extrapolated submodels is defined to account for the semantics of indicative conditionals.In this paper,the authors argue that this extrapolationist proposal has unnecessary complexity and may yield incorrect results first,and then offer an“epistemic filter”account of indicative conditionals that,the authors believe,can successfully avoid these problems.

1 Introduction

There are two different kinds of conditionals in English: indicative and subjunctive.1It is assumed in this paper that they differ not only grammatically,but also,though not everyone will agree,semantically.E.g.,R.Stalnaker ([11]) and D.Edgington ([4]),will prefer a semantically unified semantic treatment for both kinds of conditionals.An OK pair,as called by [4],is a pair of an indicative conditional and a subjunctive conditional that have the same antecedent and succedent yet differ in their truth-values.In what follows,we use “φ →ψ” and “φ ＞ψ” to stand for,respectively,an indicative conditional and a subjunctive conditional.The standard example of an OK pair is the following one (the intuitive truth-values of which are attached behind them):2This standard example is from E.Adams.([1])

(1a) If Oswald did not kill Kennedy,someone else did.(T)

(1b) If Oswald had not killed Kennedy,someone else would have.(F)

Notice that the truth of(1a)is especially obvious when an investigation was going on without reaching the conclusion that it was Oswald who killed Kennedy,while the falsity of(1b)is especially obvious when the investigation was over and the conclusion reached was that it was Oswald who killed Kennedy.Since(1a)and(1b)have the same antecedent and succedent but differ in their truth-values,the operators contained in them,i.e.,“→” and “＞”,must differ in meaning.The problem remains:how should we account for this semantic difference?

There are several answers to this question,the most popular one no doubt being the one proposed by [8] and [7] which takes an indicative conditional to be a material implication and interprets a subjunctive conditional in terms of the closestpossible-world semantics.Our focus in this paper,however,is on another answer that was recently proposed by[3].In terms of causal models,[3]proposes the following answer to our question: a subjunctive conditional should be interpreted as an interventionist conditional as proposed by [2,5,6,12],while an indicative conditional should be understood as an “extrapolationist conditional” of their proposal.To be more specific,[3]proposes that(to be explained in more details in the next section):

(CC) “φ ＞ψ”is true in a causal modelM,if and only if,“ψ”is true in the submodelM(φ).

(IC) “φ →ψ”is true in a causal modelMrelative to a contextciff either(i)M[φ]is empty,or (ii)“ψ”is true in all minimal extrapolated submodels in M[φ]as ordered by the priority relation provided byc.

Notice that(CC)is defined w.r.t.a model,while(IC)is defined w.r.t.both a model and a contextc.

We will side with[3]in accepting(CC),but we don’t think that it is a good idea to accept(IC).We will explain the main ideas contained in(IC)in Section 2,point out several problems of accepting(IC)in Section 3,and then propose our own account of the semantics for indicative conditionals in Section 4.

2 The Semantics for(IC)Proposed by Deng&Lee

Beside(1a)and(1b),[3]gives two more examples of OK pair.Here is one of them(Imagine that a fair coin was tossed and landed head,but you had bet tail.For the intuitive falsity of(2a),imagine that it was asserted before the toss and before you bet；for the intuitive truth of(2b),imaging that it was asserted after the toss and after you bet):

(2a) If you bet head,you will win.(F)

(2b) If you had bet head,you would have won.(T)

Here is another example(Imagine: you know that the local weather is such that if the atmospheric pressure is low,a rainstorm will be approaching,and that if otherwise,then a sandstorm will be approaching.Moreover,you know that you will see a black pillar of cloud in either case.For the intuitive truth of (3a),imagine that it was asserted before you saw a rainstorm；for the intuitive falsity of(3b),imaging that it was asserted after you saw a rainstorm3We actually do not have a strong intuition that(3b)should be false.However,for the purpose of this paper,we will assume that Deng &Lee are right in claiming that (3b) is false when uttered after you saw a rainstorm.):

(3a) If a rainstorm is not approaching,I will see a black pillar of cloud.(T)

(3b) If a rainstorm had not been approaching,I would have seen a black pillar of cloud.(F)

These three examples and their accompanied intuitive truth-values are the only OK pairs that [3] have considered and tried to capture by their account.As we mentioned in the beginning of this paper,their account consists of the following pair of stipulations of truth-conditions for subjunctive conditionals (CC) and for indicative conditionals(IC):

(CC) “φ ＞ψ”is true in a causal modelM,if and only if“ψ”is true in the submodelM(φ).

(IC) “φ →ψ”is true in a causal modelMrelative to a contextciff either(i)M[φ]is empty,or (ii)“ψ”is true in all minimal extrapolated submodels in M[φ]as ordered by the priority relation provided byc.

We assume that readers of this paper are already familiar with the interventionist account of subjunctive conditionals,so that if they apply(CC)to cases(1b)-(3b),they will see that all of them have the intuitive truth-valued according to (CC).So far,their account seems to be right；the problem,however,is whether(IC) captures the intuitive truth values of(1a)-(3a)?

In order to see the merit of their account,let us briefly explain what are involved in(IC).First,according to[3],a causal modelM=〈U,V,F,A〉satisfies the following three conditions:

(i)UandVare finite sets of variables,which are called “exogenous variables”and“endogenous variables”respectively；

(ii)Fis a set of structural equations specifying the causal relationships among variables.For eachVi ∈V,Fcontains exactly one structural equation which tells us howViis a function of its“parents”；

(iii)Aassigns values to each member ofUin the model.

Second,ifM=〈U,V,F,A〉,then M[φ]is the set of all models〈U,V,F,A*〉that are“extrapolated fromM”,i.e.,it is the set of all models that keepU,VandFunchanged but satisfy the condition thatφis true according toA*.Third,since there may be more than one models in M[φ],it is desirable(and actually necessary)to order them by some“priority relation”provided by a contextc,otherwise,we won’t get the desired truthvalues when evaluating (1a)-(3a).Fourth,the way a contextcprovides the priority relation is via two complex procedures: first,the contextcorders variables inU ∪Vby a total preorder；second,with this priority relation among variables in hand,the contextcthen determines a total preorder for extrapolated submodels in M[φ]by some kind of lexicographical order.The idea is that,when we compare the extrapolated submodels,we start with those variables that have a top priority to be held fixed,so that any submodel that diverges from actualMat these variables should be judged as more deviant than others.A extrapolated model in M[φ]which is not more deviant than any other model in M[φ]is called“a minimal extrapolated submodel”in M[φ].Finally,we use the set of minimal extrapolated submodels,denoted by min(M[φ]),to determine whether“φ →ψ”is true inMrelative to contextc.

In short,in order to see what truth-value that an indicative conditional“φ →ψ”has relative to a modelMand a contextc,Deng&Lee’s proposal requires us to go through the following procedure:

Step 1.[M+φ]⇒M[φ]；i.e.use the modelMand the antecedentφto determine the extrapolated set M[φ]of submodels.

Step 2.[M[φ]+c]⇒priority relation⇒min(M[φ])；i.e.,use M[φ]and the contextcto determine,via a priority relation offered byc,the set of minimal extrapolated models relative toc.

Step 3.[M,c,min(M[φ])]⇒evaluate the truth-value of“φ →ψ”inMrelative tocby(IC).

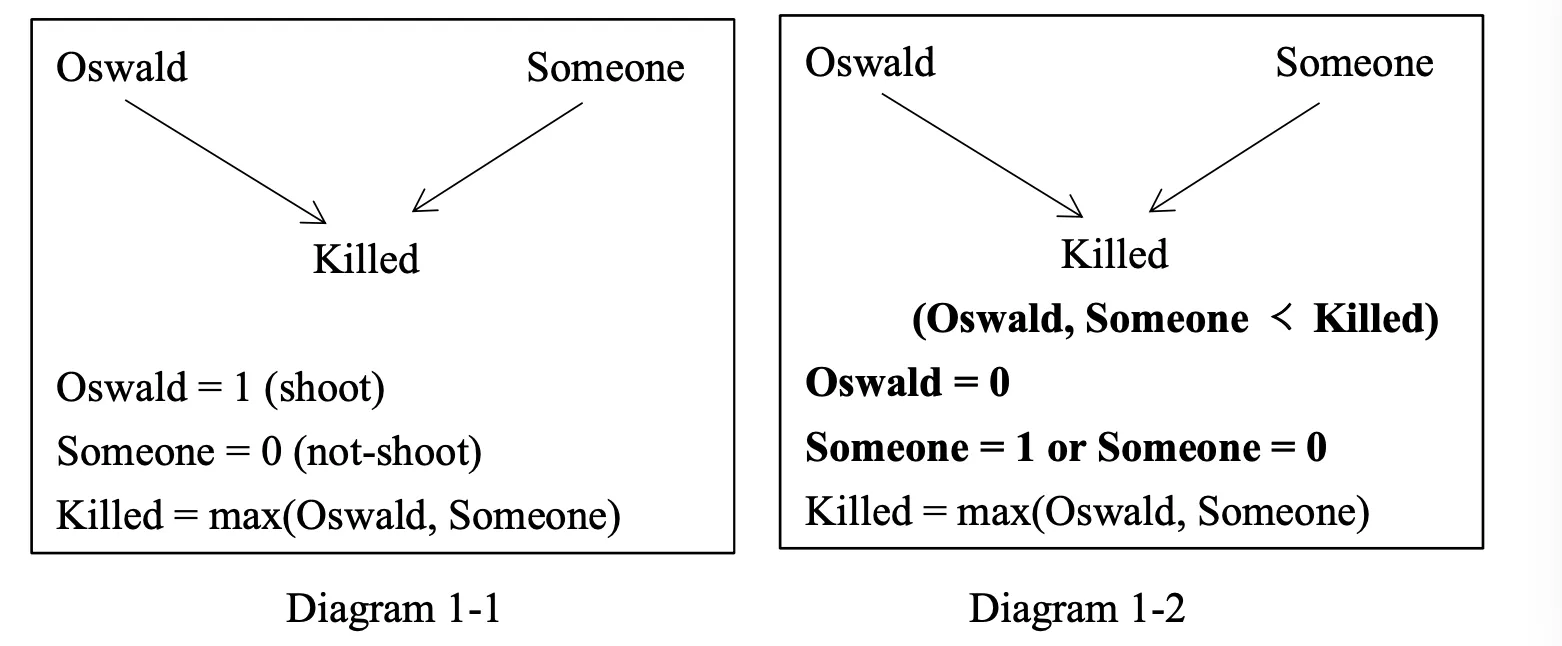
A brief revisit of the previous three examples will allow us to see how Deng&Lee’s proposal works for them.For(1a),the modelM1=〈U1,V1,F1,A1〉in question is such thatU1={Oswald,Someone},V1={Killed},F1={Killed=max({Oswald,Someone})}andA1is such thatA1(Oswald)=1 andA1(Someone)=0,as indicated by Diagram 1-1.

In order to evaluate the indicative conditional (1a),we go through the 3 steps mentioned above.After step 1,it can easily be seen that there are two extrapolated models in M[Oswald=0],as indicated by“Oswald=0”and“Someone=1 or Someone=0”in Diagram 1-2.If all these models in M[Oswald=0]were in min(M[Oswald=0]),then (1a) would not be evaluated as true,as desired,inM1relative toc(because the extrapolated model that assigns 0 to both Oswald and Someone will assign 0 to Killed too).Hence the contextccomes in as a rescuer；it takes the fact that Kennedy was killed to be the most important fact to “be fixed” or to be presupposed by the speakers in the context (don’t ask why),as indicated in Diagram 1-2 by “Oswald,Someone≺Killed”,and orders the two models accordingly so that the minimal one is the one that assigns 1 to Someone(because the other extrapolated model will deny this important fact).Since the succedent of (1a) is also true in this unique minimal model in M[Oswald=0],the indicative conditional(1a)is evaluated as true,as desired.

For(2a),the modelM2=〈U2,V2,F2,A2〉in question is such thatU2={Bet,Land},V2={Win},F2={Win=(Bet=Land)}andA2is such thatA1(Bet)=0(tail)andA2(Land)=1(head),as indicated by Diagram 2-1.

Again,in order to evaluate the indicative conditional(2a),we go through the 3 steps mentioned above.After step 1,it is easy to see that there are two extrapolated models in M[Bet=1],as indicated by“Bet=1”and“Land=1 or Land=0”in Diagram 2-2.This time,however,the context presupposes no fact at all,as indicated by“Bet≈Land≈Win”,so that all these models in M[Bet=1]are also in min(M[Bet=1]).Since the succedent of(2a)is not true in one of these minimal models in M[Bet=1](i.e.,not true in the extrapolated model that assigns 1 to Bet but 0 to Land),the indicative conditional(2a)is evaluated as false,as desired.

For(3a),the modelM3=〈U3,V3,F3,A3〉in question is such thatU3={Pressure},V3={Rainstorm,Sandstorm,Cloud},F3={Rainstorm=Pressure,Sandstorm=1-Pressure,Cloud=max({Rainstorm,Sandstorm})}andA3is such thatA3(Pressure)=1,as indicated by Diagram 3-1.

Again,in order to evaluate the indicative conditional(3a),we go through the 3 steps mentioned above.After step 1,it is easy to see that there is only one extrapolated model in M[Rainstorm=0],as indicated by“Pressure=0”in Diagram 3-2.Since the context presupposes nothing,so this extrapolated model is also in min(M[Rainstorm=0]).Since the succedent of (3a) is true in this minimal model in M[Rainstorm=0],the indicative conditional(3a)is evaluated as true,as desired.

3 Problems of Their Proposal and a Proposed Modification

So far,Deng &Lee’s account looks good.However,we will point out three problems of their account in this section and propose a simplified modification of it,so that,even if our final proposal in Section 4 won’t work out eventually,the modified version is to be preferred than theirs.Recall that the proposal of[3]requires us to go through three steps when evaluating the truth-value of an indicative conditional.We shall argue in this section that(i)the 1st step of their procedure has the problem that the complexity is high；(ii)the 2nd step of their procedure has the problems that(a)the ordering of extrapolated models via the priority relation provided by the contextcwill either be incorrect or bead hocand(b)the ordering is unnecessarily complicated(and even unnecessary)；and(iii)the 3rd step of their procedure has the problem that it may give the wrong result for indicative conditionals with“impossible”antecedents.We will explain these problems one by one.

The first step in[3]asks us to use the modelMand the antecedentφto determine the extrapolated set M[φ]of submodels,yet it is easy to see that,whenever there arenexogenous variables in the modelMother than those mentioned or involved4An exogenous variable is involved in the antecedent iff it is an ancestor of some variable mentioned in the antecedent.in the antecedent,there will be 2nmodels in M[φ]to be ordered by the priority relation.This problem can be illustrated by a simple example.Consider the following scenario: both Oswald and John were assigned the task to shoot Kennedy,though John somehow changed his mind when Kennedy’s car was approaching.At the same time,Kennedy’s two cooks,Mary and Jane,were preparing dinner for Kennedy.If Kennedy had not been killed,he would have had the dinner.In terms of causal model for this scenario,there will be 4 exogenous variables in this model: Oswald,John,MaryC(Mary cooks)and JaneC(Jane cooks),as indicated in Diagram 4.

Now,in order to evaluate an indicative conditional of the form“If Oswald did not kill Kennedy,ψ” with respect to this scenario,Deng &Lee’s account requires us to consider every extrapolated model that makes the antecedent true.In this case,there are actually eight extrapolated models in M[Oswald=0],differing only in assigning different values to the other three exogenous variables—John,MaryC,JaneC—that are not mentioned in the antecedent:〈1,1,1〉,〈1,1,0〉,〈1,0,1〉,〈1,0,0〉,〈0,1,1〉,〈0,1,0〉,〈0,0,1〉,〈0,0,0〉.From this example,one can easily see that,whenever there arenexogenous variables in a model other than those mentioned or involved in the antecedent,there will be 2nmodels in M[φ]to be ordered by the priority relation.

The problem of complexity involved in the 1st step may not impress logicians and philosophers,yet there are more serious problems in the 2nd step of the account of[3].Once we have the set M[φ]of extrapolated submodels,the next step is to use M[φ]and the contextcto determine the set of minimal extrapolated models relative tocvia the priority relation provided by the contextc.There are,however,two problems in this step: (a) the ordering of extrapolated models via the priority relation provided by the contextcwill either be incorrect or bead hocand(b)the ordering is unnecessarily complicated.

To see the problem(a),let us consider again the scenario considered in Diagram 4 and the indicative conditional“If Oswald did not kill Kennedy,Mary still cooked for Kennedy”.This indicative conditional seems to us to be intuitively true,especially when the investigation was still going on and the detective knew that the dinner had been prepared but unfortunately could not be enjoyed by Kennedy.Now,if we take all those eight extrapolated models mentioned in the previous paragraph to be minimal,then the conditional will be evaluated as false which is intuitively incorrect.So,in order to match with our intuition,the priority relation provided bycmust order 4 of them—those that assign 0 to MaryC—as more distant than the other four.Yet,what reason(s)can one give for such an ordering? What can justify our assertion that the contextcwill provide such a priority relation? Nothing except that,otherwise,we won’t get our intuition right—but this reply is obviouslyad hoc.5In[3],Deng&Lee do not say much about the mechanism that determines the priority relation in a context c,and we don’t think that they can.Specifying the underlying mechanism in a context of conversation is probably the most notorious problem in logic and the philosophy of language.

To see the problem of (b) above,notice that the main purpose of the priority relation of a contextcis to determine a set of“the most important truths in a modelM”,referred to as ΔM,c,which is supposed to be fixed or presupposed incso that any extrapolated model that disagrees with ΔM,cwill be excluded as non-minimal w.r.t.M.If this is right,then,instead of ordering extrapolated models fromMvia ordering variables,we can simply take a contextcto be a function that takes several factors incas arguments and gives ΔM,cas its value,and then use ΔM,cto“filter out”those extrapolated models that are not minimal(see(IC*)below for details).

Finally,the 3rd step of applying(IC)to an indicative conditional has the problem that it may give the wrong result for conditionals with“impossible”antecedents w.r.t.a modelM.A conditional has an impossible antecedent w.r.t.a modelM=〈U,V,F,A〉iff its antecedent is not true no matter how one changes the value assignmentA.A simple example is enough to explain this problem.Consider again the scenario described for Diagram 4 with two more added bits of information: (i)John was actually assigned as a backup assassinator for the event: if Oswald did not shoot,then John would,and(ii)the fact that Kennedy had a dinner cooked by Mary and Jane always make these cooks very happy,as indicated by Diagram 5 to the right.Now imagine someone who did not know that Kennedy was killed at that night but uttered(4) “If Kennedy ate dinner that night,Mary and Jane would be very unhappy”.It seems to us that this utterance is false rather than true.However,if we apply(IC)to this indicative conditional,it will be evaluated as true because M[EDinner=1]is empty and the antecedent“Kenney ate dinner that night”is impossible.

There is a simple way to avoid some of the problems mentioned above,especially the problem in the 3rd step and the problem (b) in the 2nd step；what is needed is only a small modification of(IC)in[3].The ideas contained in the modification are simple: (i) we take an indicative conditional with an impossible antecedent w.r.t.a modelMto behave in a similar way inMto a subjunctive conditional with the same antecedent and succedent.(ii)we take a contextcto be a function from several factors incto a set of truth ΔM,crelative toMand take min(M[φ])to be the set of minimal extrapolated submodels “filtered in” by ΔM,c,i.e.,the set of minimal models that make each member of ΔM,ctrue.With these ideas,instead of(IC),i.e.,

(IC) “φ →ψ”is true in a causal modelMrelative to a contextciff either(i)M[φ]is empty,or (ii)“ψ”is true in all minimal extrapolated submodels in M[φ]as ordered by the priority relation provided byc.

we take the following (IC*) to be a better stipulation for the truth-condition of an indicative conditional in a modelMthan Deng&Lee’s([3]):

(IC*) “φ →ψ”is true in a causal modelMrelative to a contextciff either(i)M[φ]is empty andφ ＞ψis true inM,or(ii)M[φ]is not empty and“ψ”is true in all minimal extrapolated submodels in M[φ]that are filtered in by ΔM,c.

One can check that(4)are now false according to(IC*),as desired,while(1a)-(3a)still have the same truth-values as they have according to(IC).

4 A New Semantics for IC

Can(IC)and(IC*)be further improved? Can all the problems mentioned in the previous section be avoided at once? We think the answer is“Yes”,but it will take a more radical deviation from the basic ideas contained in[3].We now explain how this can be done.

Let us start with a distinction that Pearlet al.([10],Ch.4,pp.254–260)made several times,though our distinction is a bit different from theirs6They allow that a PSSCM may not have an equation for each endogenous variable.；the distinction is between a fully specified structural causal model(FSSCM)and a partially specified structural causal model(PSSCM).An FSSCM is a quadruple〈U,V,F,A〉satisfying the following three conditions that we mentioned before: (i)UandVare finite sets of variables；(ii)Fis a set of structural equations；and(iii)Aassigns values to each member ofU,while a PSSCM is a similar quadruple〈U,V,F,A〉yet the functionAin it is only a partial function,i.e.,some members ofUmay not be defined.Intuitively,an FSSCM corresponds to a situation in which the subject has complete information about the values of all exogenous variables,while a PSSCM corresponds to a situation in which the subject has only incomplete information about the values of these variables.Pearlet al.([9,10])remind us that PSSCMs are usually more realistic than FSSCMs in that researchers usually do not have full information about models that they are dealing with.

Why is this distinction important? Because,it seems to us,a typical situation to utter an indictive conditional,unlike that to utter a counterfactual conditional,is when one has only partial or incomplete information about what are involved in a model.To see this,one needs only to check again those cases that we mentioned in Section 2: (1a)-(3a)have their intuitive truth-values partly because the speaker does not know part of the facts involved in the model；especially,s/he lacks information about some exogenous variables.

The second thing we want to emphasize before making our proposal is the important role that a context plays when evaluating an indicative conditional.[3]briefly mentions that role and,we think,they are right to say that“[the]indicatives are epistemic in that they are about the world as we(now)know[or believe]it plus the supposition of its antecedent.”As to the question how our knowledge about the world in a context affects our evaluation of an indicative conditional,we think they are right again in saying that “in general,factors [in a context] such as conversational purposes,the subject’s beliefs,the shared presuppositions,etc.,may all play a role in determining which[facts]7They actually use“variables”rather than“facts”in their paper,but the effect is the same: variable with assigned truth-values decides which simple facts are to be fixed.are to be held fixed and which can be altered”.

In short,a contextchas two roles to play when evaluating the utterance of an indicative conditional: first,the typical context for adequately uttering an indicative conditional is when the speaker does not have full information about the model in the context；second,factors in a context will determine a set of facts in the context to be held fixed or to be presupposed when evaluating an indicative conditional.

If what we have said so far in this section are correct,we propose that we should define “true-in-a-PSSCM relative toc” for indicative conditionals first,then use it to define “true-in-a-FSSCM relative toc”.For us,such an approach to indicative conditionals is to“treat an indicative conditional as an epistemic filter conditional”.

Starting with the idea of “true-in-a-PSSCM relative toc”,we propose the following truth-condition(FCP)for an indicative conditional in a PSSCM relative to a contextc:

(FCP) “φ →ψ”is true in a PSSCMM=〈U,V,F,A〉relative to a contextciff(i)“φ”is impossible inMand“φ ＞ψ”is true inM,or(ii)“ψ”is possible inMandPr(ψ |φ,ΔM,c)=1 inM8Or,equivalently,ψ is true in every FSSCM M′that“extends”M and satisfies{φ}∪ΔM,c,where a model M′extends M iff M′does not change anything in M but contains more“information”than M.,where ΔM,cis the set of simple facts aboutUthat are held fixed inc.

With (FCP) in hands,we can now see how it recasts those examples that we have mentioned in the previous sections.For(1a),it was reminded that the assertion of(1a)is intuitively true especially when the investigation was going on without reaching the conclusion that it was Oswald who killed Kennedy.If that is so,then the proper situation for uttering(1a)is represented,not by Diagram 1-1,but by Diagram 6-1:9

Now,since the antecedent“Oswald did not kill Kennedy”of(1a)is possible inM,in order to decide the truth-value of (1a) relative to Diagram 6-1 by (FCP),we use the antecedent and the presupposed set ΔM,c={Killed=1}as conditions to calculate the conditional probability of “S=1”.SincePr(S=1| O=0,K=1)=1 as indicated by Diagram 6-2(we filter out those lines that are incompatible with the conditions in Diagram 6-2),we reach the conclusion that (1a) is true by(FCP),as desired.

For(2a),it was reminded that the assertion of(2a)is intuitively false especially before the toss of the coin and before the bet.If that is so,then the proper situation for uttering(2a)is represented,not by Diagram 2-1,but by Diagram 7-1 below:

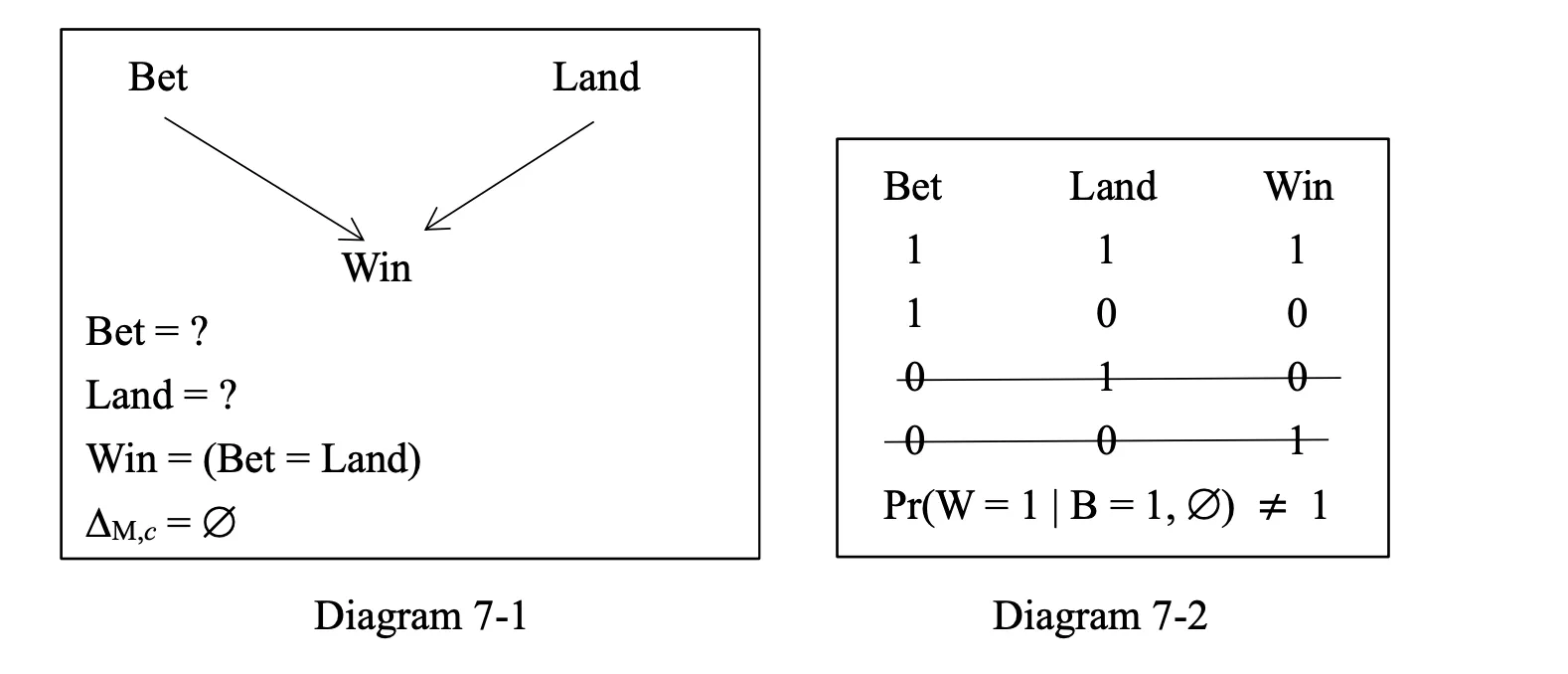
Now,since the antecedent“You bet head”of(2a)is possible inM,in order to decide the truth-value of(2a)relative to Diagram 7-1 by(FCP),we use the antecedent and the presupposed set ΔM,c=∅as conditions to calculate the conditional probability of “W=1”.SincePr(W=1| B=1,∅)1 as indicated by Diagram 7-2(assuming thatPr(B=0,L=1)0；again,we filter out those lines that are incompatible with the conditions in Diagram 7-2),we reach the conclusion that(1a)is false by(FCP),as desired.

For(3a),it was reminded that the assertion of(3a)is intuitively true especially before you saw a rainstorm and therefore before you know the pressure.If that is so,then the proper situation for uttering(3a)is represented,not by Diagram 3-1,but by Diagram 8-1 below:

Now,since the antecedent“A rainstorm isn’t approaching”of(3a)is possible inM,in order to decide the truth-value of(3a)relative to Diagram 8-1 by(FCP),we use the antecedent and the presupposed set ΔM,c=∅as conditions to calculate the conditional probability of“Cloud=1”.SincePr(Cloud=1|Rainstorm=0,∅)=1 as indicated by Diagram 8-2(again,we filter out the line that are incompatible with the conditions in Diagram 8-2),we reach the conclusion that (3a) is true by (FCP),as desired.

These examples show that our(FCP)judges(1a)-(3a)as having the same truthvalues as judged by(IC)of[3],but they do not show us how the complexity problem mentioned in Section 3 is to be avoided.To see how (FCP) avoids the complexity problem,think again the scenario for Diagram 4: Oswald and John were suspected by the detective to be the unique assassinator of Kennedy.At the same time,Kennedy’s two cooks,Mary and Jane,were known by the detector detective to be preparing the dinner for Kennedy.If Kennedy had not been killed that night,he would have had the dinner.In this case,it is intuitively true for the detector detective to assert (5):“If Oswald did not Killed Kennedy,Mary would still cook for Kennedy”.Clearly,the proper situation for uttering(5)is represented,not by Diagram 4,but by Diagram 9-1 below:

Now,since the antecedent “Oswald did not kill Kennedy” of (5a) is possible inM,in order to decide the truth-value of (5a) relative to Diagram 9-1 by (FCP),we use the antecedent and the presupposed set ΔM,c={Killed=1}as conditions to calculate the conditional probability of “MaryC=1”.SincePr(MaryC=1|O=0,K=1)=1 as indicated by Diagram 9-2(we filter out those lines that are incompatible with the conditions in Diagram 9-2),we reach the conclusion that(1a)is true by(FCP),as desired.In this case,we need only to consider four possibilities that are related to the detective’s ignorance,as shown in Diagram 9-2.If,however,we use (IC) of [3],we will,first of all,need to consider eight extrapolated models.This shows us how the complexity problems can in general be avoided: we just keep intact those simple facts that we have already known.

So far,we have only defined the truth condition for an indicative conditional in a PSSCM relative to a contextc.What if the model is an FSSCM?In order to define the truth-condition for an indicative conditional in an FSSCM relative to the same context c,let us first give the following definition:

Definition 1(exogenous cause).Y=yis anexogenous causeofX=xinMiff(i)YX,(ii)Yis an exogenous variable inM,(iii)Yis an ancestor ofX,and(iv)A(Y=y)=1 inM.

Notice that,by(i)above,a fact about an exogenous variable in a model is not an exogenous cause of itself.We now call a PSSCMM′“thetruncated modelof an FSSCMMw.r.t.‘φ →ψ’ relative toc” iffM′is just likeMexcept thatM′has no information about the exogenous causes of ΔM,cand the exogenous causes of variables in“ψ”.With these definitions,one can prove: (1)the model described in Diagram 6-1 is the truncated model ofM1in Section 2 w.r.t.(1a)relative toc；(2)the model described in Diagram 7-1 is the truncated model ofM2in Section 2 w.r.t.(2a)relative toc；(3)the model described in Diagram 8-1 is the truncated model ofM3in Section 2 w.r.t.(3a)relative toc；and(4)the model described in Diagram 9-1 is the truncated model of the model described in Diagram 4 in Section 3 w.r.t.(5)relative toc.

We now propose the following truth-condition (FCF) for an indicative conditional in a FSSCM relative to a contextc:

(FCF) “φ →ψ”is true in an FSSCMM=〈U,V,F,A〉relative to a contextciff“φ →ψ”is true in the truncated PSSCM model ofMw.r.t.“φ →ψ”relative toc.

The idea of (FCF) is simple: in case the utterance of an indicative conditional is suitable with full information about a model,not only does the contextcwill“hold fixed”some known facts in the model,it will also suggest that some known exogenous causes,i.e.,those of ΔM,cand the succedent of the conditional,should be ignored.With(FCF)and the four claims in the last paragraph,one can easily prove that: (1a)-(5) have the desired truth-value in the same contextcno matter in an FSSCM or in a PSSCM.