Counterfactual Triviality and Structural Causal Models*

Xiaoan Wu

Abstract.J.Williams(2012)proposes a version of counterfactual triviality(CT).I carefully examine the four premises on which Williams’CT relies.Within the framework of the Structural Causal Model(SCM),I show that two of them(CRT and CVPP)apply to two different types of counterfactuals respectively,so that the PA(C)of them is not equivalent,thus proving that Williams’version of CT is not valid.

1 Introduction

In the discussion of conditionals,the following two categories are generally involved:indicativeconditionals andcounterfactualconditionals.Although the distinction between these two types of conditionals is not so clear in Chinese (at least syntactically),in English there is a clear grammatical form to distinguish these two types of conditionals.There is a lot of discussion about the connections and differences between them.First of all,the semantics of these two types of conditionals are indeed distinct.For example,if it is knownJourney to the Westwas actually written by Wu Cheng’en.If we “indicatively” suppose Wu Cheng’en did not write the book,then it can be assumed that someone else wrote it；But if we “subjunctively”suppose Wu Cheng’en hadn’t written the book,it is likely nobody would have written the book.

Second,these two types of supposition play different roles in different life situations.In hypothesis testing and confirmation,indicative suppositions play an important role.If evidenceEsupports hypothesisH,thenEis more likely to occur under the indicative suppositionHthan the indicative supposition¬H.Counterfactual supposition is important in many areas,including decision-making,blame,explanation,and diagnosis.When it is counterfactually assumed that a person did not set the fire,we can infer that the fire would not have occurred and we would judge that the person is inescapably responsible for the fire and should be punished by law.

Finally,just as it is debated whether or not indicative conditionals have truth values (for example,Adams in [1] argues indicative conditionals do not have truth values.),there is a debate over whether counterfactual conditionals are truth-valued propositions.For instance,Edgington ([7]) argues that counterfactuals are simply expressions of our belief-modification strategies.Some people believe that counterfactuals are only assertable,acceptable,or probabilistic,but have no truth value.But intuitively we believe or accept a counterfactual conditional with its truth in mind.Thus Hájek ([10]) believes if a counterfactual has no truth value,it is difficult to understand how a counterfactual is probabilistic.Convinced by Hájek’s arguments,let’s accept the assumption that the counterfactuals have truth value and continue our discussion.

So the next question is: to what degree should we believe in a conditional? There is an admittedly fairly reasonable restriction on the degree of conditionals,commonly known as theRamsey test:

If two people are arguing‘Ifp,thenq?’ and are both in doubt as top,they are addingphypothetically to their stock of knowledge and arguing on that basis aboutq；so that in a sense‘Ifp,q’and‘Ifp,¬q’are contradictories.We can say that they are fixing their degree of belief inqgivenp.Ifpturns out false,these degrees of belief are rendered void.If either party believes notpfor certain,the question ceases to mean anything to him except as a question about what follows from certain laws or hypotheses.([28],p.143)

The above statements are still unclear.First,what does it mean to “addphypothetically to their stock of knowledge”? As noted above,there are at least two different kinds of supposition,one that is an indicative supposition and the other is a counterfactual supposition.Different suppositions correspond to two different types of conditionals in natural language,counterfactual conditionals and indicative conditionals,and different types of conditionals also correspond to different degrees of belief,that is,through the indicative supposition,we determine our credence for indicative conditionals,and through the subjunctive supposition,we determine credence for a counterfactual.

Second,how should we characterize and represent the above “adding”? The Ramsay test is generally understood as the conditions under which we can reasonably believe a conditional.That is,if he accepts the consequent under the supposition that the antecedent holds,then he should accept the conditional.In the framework of credence or subjective probability,it can be restated as: One’s degree of rational belief in a conditionalp →qshould equal one’s degree of credence inq,under the supposition thatp.Different understandings of the above suppositions and credence have in turn produced different ways to characterize and represent the above“adding”,resulting in different versions of the Ramsay test.

Our credence in an indicative conditionalA →Bshould equal one’s credence in the consequentBon the indicative supposition of its antecedentA.That is,the Indicative Ramsey Test(IRT),formally expressed as:

The above formula links the conditional to the credence.Intuitively,the above formula is acceptable.If it is assumed that Wu Cheng’en did not writeJourney to the West(that is,Wu Cheng’en did not actually writeJourney to the West),then there is a high probability thatJourney to the Westwas written by someone else,and likewise,you have a high probability of accepting the conditional “If Wu Cheng’en did not writeJourney to the West,then someone else wrote the book”.

Our credence in a counterfactual conditionalA □→Bshould equal one’s credence in the consequentBon the subjunctive supposition of its antecedentA.That is,the Counterfactual Ramsey Test(CRT),formally expressed as:

In fact,the possible world semantics given by Stalnaker ([36]) and Lewis ([16]) to determine the truth value of a counterfactual is consistent with the idea of CRT.According to Lewis,the truth value of the counterfactualA □→Bin the actual world is determined by the truth value ofBin theA-world closest to the actual world.

But if introducing credence and accepting that a counterfactual’s truth value affects our credence in it,then CRT does not seem to hold.For example,considering the counterfactual“If I had flipped this fair coin,it would have landed heads(A □→B)”,assuming the antecedent is true,and the confidence in the consequent is 50%.But according to their semantics,because there does not exist anA ∧B-world closer to the actual world than anyA∧¬B-world,so the counterfactualA □→Bis false,then our credence in it is relatively low,less than 50%,so CRT is not valid.

Given that in our subsequent discussion of CT,the possible world semantics of counterfactuals are not a premise and basis we have to adhere to,so let us accept CRT for the time being,which is intuitively reasonable.If you counterfactually suppose that Wu Cheng’en hadn’t writtenJourney to the West,and you think there is a high probability that nobody would have written the bookJourney to the West,then it seems equally reasonable to agree that the following counterfactual has a great probability:If Wu Cheng’en hadn’t writtenJourney to the West,then nobody would have written the book.

Third,on standard Bayesian construals,credence under indicative supposition is identified with conditional probability.So there is one interpretation of the Ramsay test: Adams’ Thesis (AT),also known as Stalnaker’s Thesis (ST),formally expressed as:

Note that although AT and ST have the same form,the interpretations ofP(A →B) are not the same.And let us denote the different interpretations ofP(A →B)by Adams and Stalnaker byP′(A →B) andP*(A →B) respectively.Adams([2]) thinks thatP′(A →B) can be understood as expressing “the assertability ofA →B”；And Stalnaker ([37]) argues thatP*(A →B) should be understood as“the probability thatA →Bis true”,which is equivalent to the probabilityP(B |A).These different interpretations have their own validity and do not affect the next discussion,so let’s take a neutral stance on them.

Lewis([17])pointed out that no matter howP(A →B)is understood,as long asPobeys the laws of probability,then the Adams thesis plus the possible world semantics of conditionals yields the following triviality results:1The specific proof process is as follows:P(B |A)=P(A →B)=P(A →B |B)P(B)+P(A →B |¬B)P(¬B)=P′(A →B)P(B)+P′′(A →B)P(¬B)=P′(B |A)P(B)+P′′(B |A)P(¬B)=P(B |A ∧B)P(B)+P(B |A ∧¬B)P(¬B)=P(B)This proof’s validity is based on two assumptions.First, P(A →B | B)= P′(A →B) implies the assumption that →denotes the same propositional connective in any context.If P′ obtained by conditionalizing P on the proposition B (P′′ obtained by conditionalizing P on the proposition¬B),then this conditionalisation does not affect the truth condition of P(A →B).Second,P′(A →B)=P′(B |A)implies the assumption that the Adams thesis holds not only for P,but also for P′.

This triviality result implies that in non-trivial language,AT cannot be accommodated within the framework of classical possible-world semantics,and Bradley([4])also shows that even a very weak consequence of AT is not compatible with the framework of classical possible-world semantics.For a discussion of triviality problems in Chinese see Su([38])and Liu([23]).

As noted above,in the case of indicative conditionals,there are standardized ways to formalize the credence under the indicative suppositions — i.e.,by conditional probabilities.In the case of counterfactual conditionals,there is no universally accepted standard way of implementing the subjunctive suppositions,but rather a variety of positions,none of which is universally accepted.Often referred is the position of Skyrms ([35],p.261).In a critique of Adams ([3]),he replaced “prior epistemic probabilities” with “a priori propensities”,so theSkyrms’ Thesis(ST)equates credence in the counterfactual with the expectation of the corresponding conditional chances:

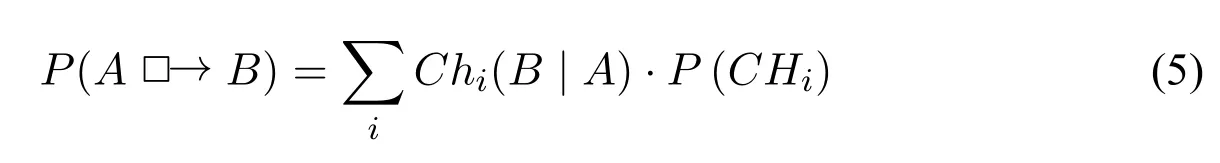
whereChiis the objective chance function andCHisays thatChiis correct about the objective chance,and further assumes that allCHi(denoted as{CHi}) are a partition of chance hypotheses.

Although very often we do not know the objective chance of a specific event or proposition,ST implies that when the objective chance of the consequent is above a certain threshold given the antecedent,then we should accept the counterfactual.Moreover,the reason for the weighted expression in equation(5)above is that we are not sure about the exact value of the conditional chance,so we have made a partition of the possible chance propositions.Finally,whether ST is true is still controversial and not generally accepted,and there are alternative ways of cashing out subjunctive supposition([31]).The above discussion can be summarized in the following figure:

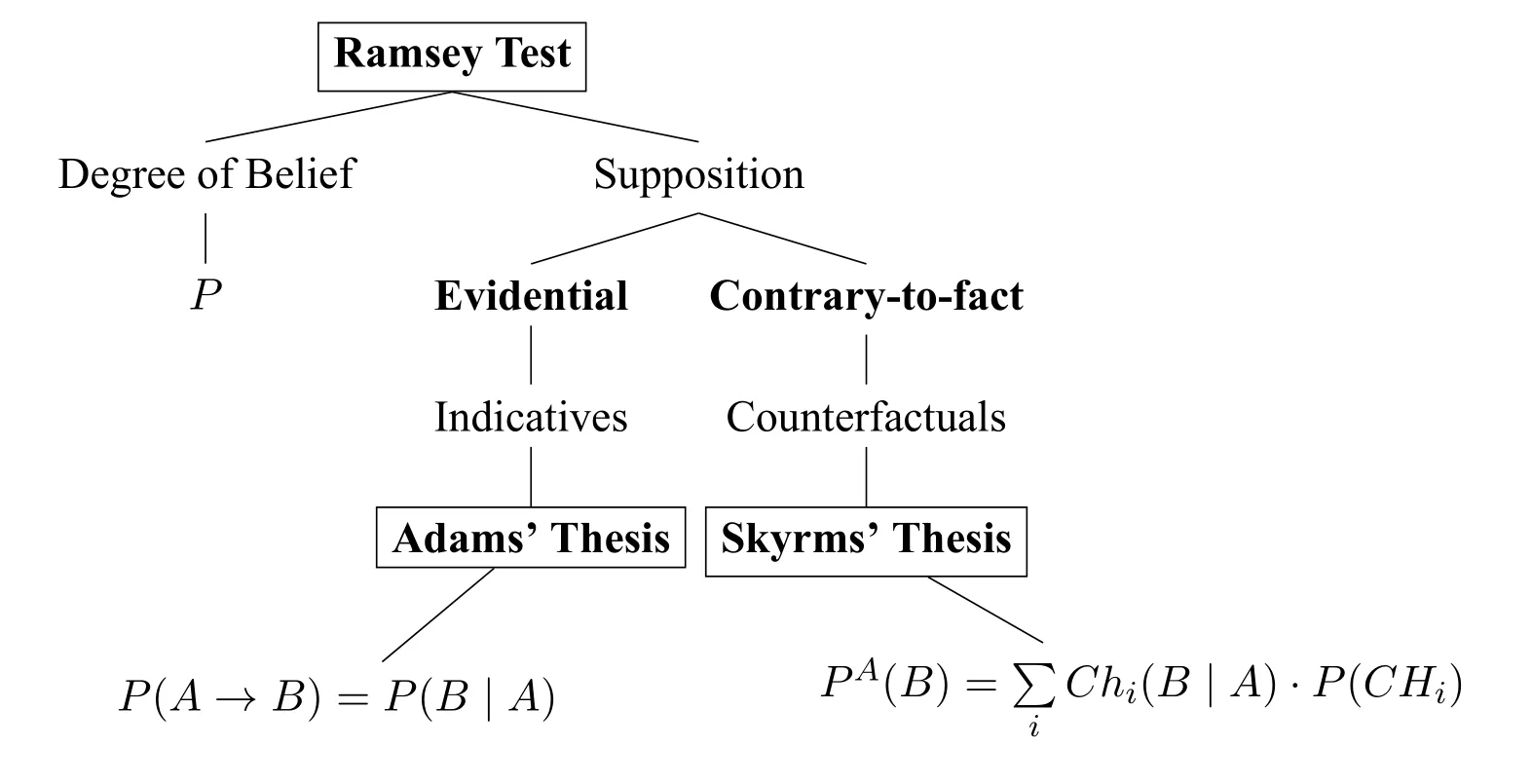
Figure 1 : The Origins of Adams’Thesis and Skyrms’Thesis

Finally,Although the triviality of indicative conditionals has been much discussed,few have heard of CT,and Williams ([39]) demonstrates that under some seemingly reasonable assumptions,we can derive CT results as follows:

First,this is obviously a very strange and absurd result.For example,consider a counterfactual conditional in Chinese: “If only the Winged General of Han were around to fight the township of Basilisk,the barbarians and their horses would never have dared to cross the Mountains of Yin”.If the above triviality holds,it means that we have the same degree of belief in the proposition“If only the Winged General of Han were around to fight the township of Basilisk,the barbarians and their horses would never have dared to cross the Mountains of Yin”as we have in the proposition that“The barbarians and their horses would never have dared to cross the Mountains of Yin”.

Second,for researchers working with SCM and potential outcomes models,CT is a very strange result,and it seems that no one has had time to think about what such a result means for SCM,this seems to be a quirk that only arises in logical contexts.If this is right,it is clearly a problem that needs to be addressed.But for now,most people are skeptical of this result([5,33]),and this paper also tries to show that this result is not true from the perspective of SCM.

2 Williams’Argument

Next,we will discuss specifically how Williams derived the triviality results.It is important to note that CT actually takes many different forms,depending on different presuppositions.Triviality results derived by Williams ([39]) are closely related to fourprima faciereasonable premises,in particular,the Principal Principle(PP),which links chance and credence,and ST (i.e.,A Conditional Version of the Principal Principle,CVPP),while other versions of the CT results are not based on these premises.For example,Santorio([30])uses six plausible hypotheses“Nonzero,Upper Bound,CRT,Restricted Suppositional Additivity,CNC and Closure”to obtain the triviality result:P(A □→B)=P(A ◇→B).This paper will focus on the triviality results given by Williams([39])and give an interpretation of the triviality results of Santorio([30])based on my solution to Williams’triviality results.

Broadly speaking,Williams’argument can be structured as below.

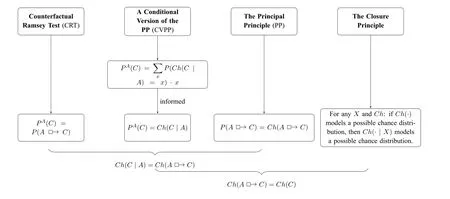
Figure 2 : Williams’Argument.

In the discussion that follows,we will analyze each of these four premises and show how they ultimately derive the triviality results.

First,as Williams([39],p.649)states,the CRT is just a normative constraint2In Williams([39]),he discusses not only the CRT(also known as his Counterfactual Ramsey Identity),but also alternative assumptions,such as Counterfactual Ramsey Bound and Counterfactual Ramsey Zero respectively,those premises also lead to absurd results.It seems that these absurd results are all based on the above assumptions and the equivalence of the PA(C)in ST and CRT,so this paper’s refutation of the argument premised on the CRT also constitutes a refutation of the other two alternative assumptions.,which means that for a fully rational agent,his categorical credence in the counterfactualA □→Band his degree of belief inBon the counterfactual supposition thatAshould coincide.There may be cases in which it is not satisfied,but if this normative constraint is correct,then the above violation is“a form of irrationality”.

Second,another important premise of Willams’ argument is PP.Lewis ([21],p.266)proposed PP(Slightly modified for consistency with the symbolic expressions in this paper).

PP.LetPbe any reasonable initial credence function.Lettbe any time.Letxbe any real number in the unit interval.LetXbe the proposition that the chance,at timet,ofA’s holding equalsx.LetEbe any proposition compatible withXthat is admissible.at timet.Then

Looking at this definition,you may find the principle very complex and involves many concepts that need further clarification,so let’s start with a simple example of the application of the principle so as to get an intuitive grasp of the principle: Suppose you are going to throw a die and you want to assign your degree of belief to various assumptions about the number of dice,what should be your degree of belief about the number of dice of 3? According to Lewis([19]),your belief in it is determined by PP.LetPdenote your subjective credence,Ais the proposition that the number of dice tossed is 3,Ch(A)=xis the proposition that the objective chance ofAisx,andEis a proposition that must beadmissible.

So PP essentially says that,in the absence ofinadmissibleinformation,your beliefs about the chance of the dice being thrown at 3 should guide your beliefs about the dice being thrown at 3:

Lewis does not give a precise definition of whatadmissibleinformation is and whatinadmissibleinformation is.Lewis ([21],p.272) says roughly: “Admissible propositions are the sort of information whose impact on credence about outcomes comes entirely by way of credence about the chances of these outcomes.”And he also gives two examples of what is generally admissible information:historical informationandhypothetical information about chance itself.The ripple effect of Lewis’s question about admissible information (and the controversy it generated) continues to this day.To take our current example,inadmissible information means that,before you throw the dice,if an omniscient prophet tells you that your next throw will be a 3,then as a rational person,your confidence that the number of dice will be 3 will be greatly increased,even though your belief in the objective chance of the number of dice being 3 has not changed.Therefore,the discussion of the relationship between chance and credence requires the absence of inadmissible information,otherwise PP would not hold.

So without inadmissible information,according to PP,we have:

Third,to understand the conditional version of the Principal Principle(CVPP),we have to start withcausal decision theory(CDT).As Joyce([15],p.161),“Causal decision theory seeks to provide a rigorous formal analysis of the idea that a rational decision maker should evaluate her potential actions solely based on their ability to cause desirable outcomes.”We can formalize this idea as a function of causal expected utility in the following form:

The probability functionPA(·)measures the agent’s estimate of the‘causal tendencies’ofA；U(A)measures the extent to which performing ofAcan lead to desirable or undesirable outcomes；and the functionu(·)represents the desirability of the agent for various states of the world.According to CDT,the agent should choose an action that maximizes the causal expected utility.

The most crucial aspect of the above equation is interpretingPA(C),which has been interpreted differently by different causal decision theorists,but as Joyce([15],p.161)points out,all of them rest on a common foundation: “PA(C)’s values should reflect a decision maker’s judgments about her ability tocausally influenceevents in the world by doingA.I will call it hercausal probability for A.”

Lewis([20],p.11)proposed a K-partition account of causal probabilities,where an elementKin a particular partition K is“a maximal specific proposition about how what [the agent] cares about depends causally on his present actions”.Like Lewis,we call the elements in K thedependency hypotheses.Thus,we have a measure of the‘causal tendencies’or causal probability forA([15],p.164):

Definition 1(K-expectation Definition of Causal Probability).IfP(A)＞0,then

for some appropriate choice of a partition of dependency hypotheses K.

The next problem is to find the appropriate K.One interpretation of K claims that dependency hypotheses provide direct specifications for objective chances.everyKcontains a complete theory of objective conditional chance such that for each eventCand actA,it implies a proposition of the formCh(C |A)=x.Thus,in the context of decision theory,we can assume that conditional chance and subjective probability are related as follows:

Definition 2(CVPP).IfPis any probability on Ω,ifP(A,K)＞0,and ifKentails that the chance ofCconditional onAisx,then

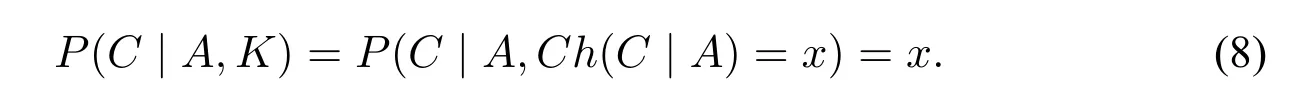
According to CVPP,the equation can be further decomposed as follows:

The result obtained above isST(cf.Eq.5)! Consider an agent who is fully informed aboutCh,the above equation simplifies to:

Fourth,The Closure Principlestates that ifCh(·)models a possible probability distribution for any propositionXand chance functionCh(·),thenCh(· | X)also models a possible probability distribution.As with “Conditional probabilities are probabilities”,there does not seem to be much hesitation in accepting this principle.

Based on the above four premises,Williams([39],p.661)derives:

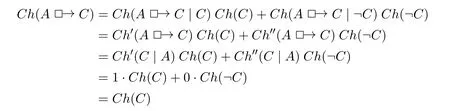
First,like indicative triviality,Ch′obtained by conditionalizingChon the propositionC,Ch(A □→C |C)=Ch′(A □→C)implies that“□→”expresses the same propositional connective in every context,so the conditionalisation do not affect the truth condition ofCh(A □→C),Williams does not specifically discuss the legitimacy of this assumption,obviously this assumption can be challenged([29]),but it is not the subject of this paper,so let’s put it aside.Second,according to CVPP,PP and CRT,we haveCh′(A □→C)=Ch′(C |A)；Third,according to PP,we can finally obtain equation(6),which yields the CT results.

3 Contra Counterfactual Triviality

Although this result is unacceptable,the four principles on which it is based seem reasonable.“Conditional probability is also a probability” is a proven probability theorem,so the Closure Principle seems feasible.PP (and CVPP) is also an intuitively compelling principle,although Lewis([22],p.473)turns to a more complex“New Principle”because of the“one big and bad bug”,the bug is problematic because of his Humean Supervenience conception of the nature of chance,the plausibility of which is not in question if the ontological position of Humean Supervenience is put aside.Schwarz([32])also gives a formal proof of PP.As mentioned before,if we hold possible worlds semantics of counterfactuals,then CRT does not hold.But given the many problems with the possible worlds semantics itself,and the fact that it can be discussed without presupposing any semantics,CRT is not problematic as a normative principle.

So each of these principles has its own focus and scope of application.First,CRT considers the conditions under which a rational agent can reasonably believe a counterfactual,or assign probabilities to counterfactuals.Note that this normative constraint does not conflict with the fact that counterfactuals are context-dependent.It is well-known that the counterfactualsA □→Bare context-dependent([34],pp.257-259),so it is reasonable to assume thatP(A □→B))is also context-dependent.A counterfactual sentence can be interpreted in multiple ways depending on the conversational context,intention and practical purpose of the speaker at the time.So for the counterfactual contextualist,the truth value of a counterfactual depends on what the speaker is trying to say when he says the counterfactual and what the hearers think the speaker is saying when he hears the counterfactual.In one context,“If Caesar had been in charge[in Korea],he would have used the atom bomb”is true,while in another context“If Caesar had been in charge[in Korea],he would have used catapults”can also be used with a high degree of belief.But in any context,credence in the counterfactual is governed by normative constraints like CRT.

Second,the objective chance is independent of the above contextual factors,and our everyday understanding of chance is consistent with the physics understanding of chance.Chance is a characterization of the objective features of the world,not a characterization of the uncertainty of an agent.The chance of a tritium atom decaying in 2023 is clearly not relevant to the context of the conversation.WhenAandCare context-independent,the conditional oddsCh(C | A)are also context-independent,according to the usual analysis:

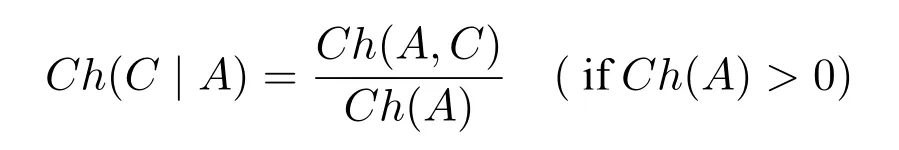
BothCh(A,C)andCh(A)are objective chances with fixed content,so they are context independent,and their ratios are also context-independent.Thus,the conditional chanceCh(C | A) is context independent.Therefore,a direct refutation of Williams’argument is that thePA(C)used in the CRT and CVPP is not equivalent.The former is compatible with the context-dependent fact of the counterfactual,while the latter abandons the context-dependence of the counterfactual altogether,but many counterfactuals are under-described,e.g.,“If Caesar had been in charge[in Korea]”and“If a chicken had lips”([13],p.1165).And without the addition of precise information,or in the absence of precise context,there is no objective chance of the above counterfactual.

In the following discussion,I will further illustrate thatPA(C) in CRT andPA(C) in CVPP are not equivalent within the framework of SCM.SCM ([25]) is a methodological model of social science developed by computer scientist Judea Pearl and his disciples.Unlike the thinking of philosophers and logicians,he is an application-oriented scientist.The focus of his thinking is not on examining universal principles and their legitimacy for counterfactuals or causation,but rather on how to construct models to answer specific counterfactual and causal inference questions.And their research is useful for philosophical and logical thinking about counterfactuals in general.This general thinking can easily lead us to ignore possible differences between specific counterfactuals and to claim premises or principles that are intuitively reasonable but not actually true,leading to absurd results.Referring to the SCM for the distinction and solution of specific counterfactuals and causal inference problems,or the algorithmic implementation of specific counterfactuals,will allow us to better understand the differences and distinctions between the counterfactuals themselves,thus clarifying the boundaries of the applicability of some general principles(e.g.,CRT and CVPP),and thus dissipating the absurd results.

The following argument will be divided into four steps: First,I will prove CRT⇔PX=x(Y=y)⇔P(X=x □→Y=y)⇔P(Yx=y |x′,y′)；Second,prove CVPP⇔PX=x(Y=y)⇔Ch(Y=y | X=x)⇔P(Y=y | do(X=x))；Third,proveP(Yx=y | x′,y′)P(Y=y | do(X=x))；Fourth,I proof that the CT is not established.

The key to the proof is to recognize that CRT and CVPP as normative constraints actually correspond to two different types of counterfactuals:retrospectivecounterfactuals andprospectivecounterfactuals,although this distinction has not yet been made explicit(These two types of counterfactuals respectively correspond to the second-level “intervention” and the third-level “counterfactual” in the Three-Level Causal Hierarchy given by Pearl).For example,Hitchcock([12],p.130)points out that the causation involved in CDT is not actual causation in the Lewisian sense:“What is distinctive about actual causation is rather that is retrospective: it involves a kind of reasoning backward from effects to their causes.By contrast,CDT is prospective: it involves reasoning forward from causes to their effects.”

Similarly,Pearl,Glymour,and Jewell([27],p.90)have argued that when driving home from work and passing a fork in the road,the inference made by choosing to take one of the roads is different from the inference made by taking that road and then counterfactually imagining what would happen if you took the other highway: “My retrospective estimate is that a freeway drive would have taken less than 1 hour,and this estimate is clearly different than my prospective estimate was,when I made the decision prior to seeing the consequences—otherwise,I would have taken the freeway to begin with.” Given the close connection between causation and counterfactuals,the counterfactuals involved in CRT are those corresponding to actual causation,i.e.,counterfactuals in the subjunctive mood,whereas CVPP is derived from CDT,and its counterfactuals are interventionist counterfactuals,which can be understood in the indicative mood.([14])

3.1 The algorithmization of counterfactuals

Within the framework of SCM,the calculation of the retrospective counterfactual follows a fixed pattern,which can be illustrated by the following paradigmatic counterfactual:

(a) If I had flipped this fair coin,it would have landed heads.

First,for the representation of the world,SCM has a Laplace’s quasi-deterministic conception that all randomness is due only to unknown causal factors,these known and unknown causal factors together constitute a deterministic conception of causation.For example,the randomness in the coin flip example is represented by the variableU:

Second,within the framework of SCM,the calculation of the counterfactual probability goes through three steps: Abduction,Action,and Prediction.The basic idea behind this is actually very simple.In order to correctly state what will happen under the counterfactual supposition,it is necessary to have an exact grasp of the real situation.therefore,a fully specified model is needed.Abduction is based on the known results to determine the specific background,then the counterfactual antecedent is realized by intervention,and finally the probability of the consequent is calculated under the condition that the antecedent occurs,and thus the probability of the counterfactual is finally determined.

For example,the probability of (a) can be calculated according to Pearl ([25],p.206).According to Abduction,we obtain:

According to action and prediction,we get:

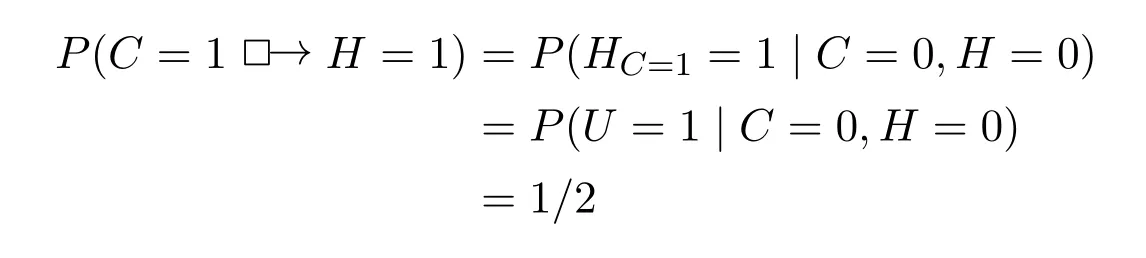
The probability of counterfactual (a) is 1/2,which fits with the intuition.So within the framework of SCM,we can have the following conclusions

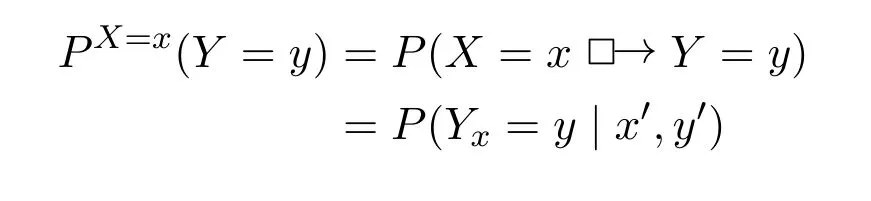
3.2 Causation decision theory

In the previous discussion on CDT,we discussed a K-partition account of causal probabilities forA(Eq.(7)),and it is known that the most difficult part of the theory here is how to understand K.Eq.(8)gives a solution: the“chance”reading of dependency hypotheses K,and there is another way of understanding belief about causal tendencies,namely the “counterfactual dependence” reading of dependency hypotheses:

We begin with a rough theory of rational decision-making.In the first place,rational decision-making involves conditional propositions: when a person weighs a major decision,it is rational for him to ask,for each act he considers,what would happen if he performed that act.It is rational,then,for him to consider propositions of the form‘If I were to doa,thencwould happen’.Such a proposition we shall call acounterfactual.([9],p.153)

So a function of causal expected utility can be expressed as follows:

The term‘□→’refers to non-backtracking counterfactuals in the sense of Lewis([18]),but since a formal method for combining chance and counterfactuals is missing,it is not clear how to computeP(A □→C),though the idea is there.

Meek and Glymour([24])pointed out that we can elaborateP(A □→C)using the formalism of doing interventions in Bayesian networks.Hitchcock([13])further demonstrates that this proposal not only helps to clarify a number of issues surrounding CDT,but also constitutes a response to many of the“exotic”counterexamples to this theory.

Although we use “counterfactuals” here,it is important to note that counterfactuals here are different from the counterfactuals mentioned in the previous section that correspond to actual causation,and are a special class of counterfactuals,as Edgington says:

Note: I shall stick to the label “counterfactual”,as most participants in the debate do,because the issue is not really one of grammar but one of function.But,not to be misled,you have to realize that these are“counterfactuals”which do not presuppose the falsity of the antecedent.It is just a convenient label for a type of conditional,a conditional which in English has a“would”in the consequent,which includes those that do presuppose the falsity of the antecedent.([8],p.78)

DeRose([6])further states that although it is widely assumed that’straightforward’future-directed conditionals that are used in CDT are counterfactual or subjunctive conditionals,he argues that the conditionals of deliberation are indicative.We do not intend to discuss in depth whether the counterfactuals used in decision theory are paradigmatic counterfactuals or indicative conditionals,but at least the counterfactuals involved in decision theory are a special class of counterfactuals,as envisioned by Meek and Glymour([24]),using Pearl’s do-operator,in the SCM,as given by Pearl([26],p.981),one can further express equation(9)as:

In summary,we have given two understandings ofPA(C),one is the“chance”reading and the other is the“counterfactual dependence”reading(or do-operator),as Lewis says: “We causal decision theorists share one common idea,and differ mainly on matters of emphasis and formulation.”([20],p.5)Harper and Skyrms also says:“It can be argued that the various forms of CDT are equivalent—that an adequate version of any one of[them]will be interdefinable with adequate versions of the others.”([11],p.x)If the above understanding is correct,then:3“As philosophers of science have long been telling us,the notions of causation,chance,counterfactual dependence,similarity among worlds,and natural law form a constellation of interrelated concepts,any one of which can be used as a starting point for an analysis of the rest.”([15],pp.171-172)

The anonymous reviewer questions the legitimacy of the above equation,“since CDT is a decision theory,the probabilities involved inU(A)must be subjective probabilities,butCh(Y=y | X=x) is an objective probability,and they cannot be equal”,while in my understanding,theP(Y=y|do(X=x)) used inU(A) is a representation of the interventionist counterfactual probabilities.According to the SCM,when there is an accurate causal diagram characterizing the specific situation and sufficient reliable data,we get the objective causal effect of the antecedent on the consequent,whileCh(Y=y |X=x)characterizes the objective probability of the consequent(Y=y)occurring if the antecedent(X=x)occurs.So it seems to me that,first of all,what they characterize is actually the same.Second,as Joyce points out,“As philosophers of science have long been telling us,the notions of causation,chance,counterfactual dependence,similarity among worlds,and natural law form a constellation of interrelated concepts,any one of which can be used as a starting point for an analysis of the rest.”([15],pp.171-172)So althoughu(A&C)inU(A)represents the desirability of the subjective agent,P(Y=y |do(X=x))characterizes the objective causal effect of the occurrence of the antecedent on the consequent.

3.3 Inequivalence in the SCM

Next we have to prove that:

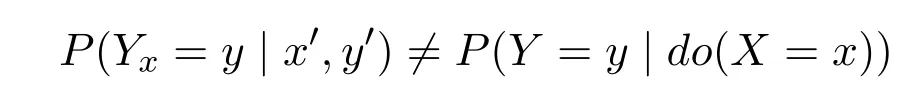
As mentioned earlier,P(Yx=y | x′,y′) is a formal characterization of the credence in the retrospective counterfactual,whileP(Y=y | do(X=x)) (orP(Yx=y))is primarily a formal characterization of the credence in the prospective counterfactual.First,the difference can be illustrated from the perspective of the possible worlds,Yx=yand (X=x′,Y=y′) inP(Yx=y | x′,y′) are events that occur in different possible worlds,(X=x′,Y=y′) in the real world,andYx=yin the counterfactual world in whichX=xholds.In order to determine the value ofYxin this counterfactual world,we need the information from the real world:(X=x′,Y=y′)；while(X=x,Y=y)inP(Y=y | do(X=x))occurs in the real world and does not involve the counterfactual world.

Second,the causal issues explored by the two representations are not the same.UsingP(Yx=y | x′,y′)is more about theCauses of Effects(CoE).For example,to determine whether receiving irradiation was the cause of the patient’s tumor recurrence(actual causation)in a realistic scenario where the patient did not receive irradiation and his tumor recurred,one must examine the credibility or truth of the counterfactual: “If I had gone through irradiation,my tumor would not have recurred.”

Because CDT is about predicting the outcome of each action option causally,the use ofP(Y=y | do(X=x)) is more aboutEffects of Causes(EoC).For example,in a realistic situation,the patient has not yet received any treatment and has two choices in front of him,either irradiation or no irradiation.The patient has to make predictions about the‘causal tendencies’of these two actions,and then choose the action that maximizes the causal expected utility based on the desirability of the various outcomes,by examining the truth or belief of the following counterfactual:“If I were to receive irradiation,then my tumor would not recur.”In the EoC quest,the potential actions under study are chosen ahead of time,whereas,in the CoE quest,the research goal is to find and access the importance of causes.From an experimentalist perspective,Yx(u)describes the behavior of a specific individualU=uunder the interventiondo(X=x)(or,of course,the behavior of a sub-population).So we can use this formal picture as a basis for discussing some ethical concepts: credit,blame,and regret.ButP(Y=y | do(X=x))characterizes the behavior of a population under a given intervention.

Third,the‘equipment’and methods needed to calculate the two are different.To compute the exact probability of the counterfactual,we need data and a fully specified model,Pearl([25],p.206)gives three steps for the computation: Abduction,Action,and Prediction.But to computeP(Y=y | do(X=x)),we just need the data and a causal diagram that correctly articulates ‘the story behind data — the causal mechanism that led to,or generated,the results we see.’ And also the action of setting a variable,X,to valuexis simulated by replacing the structural equation forXwith the equationX=x.

Finally,in general,P(Yx=y |x′,y′)cannot be expressed by a do-operator(i.e.,expressed in the formP(Y=y | do(X=x))),butP(Y=y | do(X=x))can be expressed asP(Yx=y).As Pearl,Glymour,and Jewell([27],pp.99-100)point out,P(YX=1=y′ |Z=1)andP(Y=y′ |do(X=1),Z=1)are similar in form,but they characterize very different contents and answer very different questions.

4 Conclusion

I have presented a proof showing thatPA(C)in CRT andPA(C)in CVPP have different extensions,so they are not equivalent.In turn,it is shown that CRT and CVPP are not equivalent as proved by Williams,so there is no such thing as CT.

We know that there are different versions of CT,for example,Santorio ([30])also gives a version of the triviality result which,unlike Williams’triviality results,does not involve any specific way of cashing out suppositional credence for counterfactuals (ST and CRT),nor PP,as if the triviality results could be obtained from some weaker and less controversial assumptions.But Santorio actually deals with a more complex dimension of the counterfactual: the relationship betweenwouldcounterfactuals andmight-counterfactuals.Indeed,because it does not involve the cashing out of counterfactual suppositions,the assumptions he presupposes are derived more from intuitive plausibility than from specific application contexts,and the refutation of Williams’CT does not constitute a solution to Santorio’s CT.

But I think the point of this rebuttal to Williams’CT is that,within the framework of the SCM,the kind of“counterfactual”involved in CDT is at least algorithmically different from the paradigmatic counterfactual,and I am not convinced that this means that such counterfactuals are in fact indicative conditionals,but at least it shows that we have to be very careful when we prepared to equate some norms that apply to it with norms that apply to the paradigmatic counterfactual,as Williams’CT illustrates.