A Qualitative Logical Analysis of Probabilistic Causal Models*

Kaibo Xie

Abstract.Uncertainty occurs frequently in the process of causal reasoning.Although the traditional structural equation model is very successful in the reasoning of deterministic causal structure,yet it is not designed to characterize probabilistic reasoning.Recently there have been proposals aiming to account for probabilistic causal reasoning by adding quantitative probabilistic expressions in the causal language.Contrast with the quantitative approach,this paper will present a qualitative model of probabilistic causal reasoning,which represents uncertainty of variables in terms of doxastic relations.The formal language based on this framework is able to express a qualitative notion of independence among causal variables,which can be used to analyse the co-relation between causality and probability.

1 Introduction

1.1 Toward a logical analysis of probabilistic causal reasoning

In recent years,a lot of effort has been put in the development of formal models for causal reasoning with counterfactuals.The most well-known model is the structural equation causal model developed in[8].The logical inquiry of causality based on the structural equation approach also gained a lot of popularity since[3,6,9].

A structural equation causal model includes a signatureSand a set of structural equationsF.The signatureS=(U,V,Σ)whereUis the set of exogenous variables,Vis the set of endogenous variables,and Σ is the range of those variables.The setF={fX:X ∈V}contains a structural functionfXfor each endogenous variableX ∈V,andfXmaps any assignment toU ∪V{X}to a possible value ofXin Σ.Thus,each structuralfXdescribes how the value ofXis determined by the setting of other variables.1In many studies of structural equation models, F is assumed to be recursive,which means there is no sequence X1,...,Xn such that for each 0 ＜k ＜n the value of Xk+1 is dependent on Xk according to F,and the value of X1 is also dependent on Xn.In other words,being recursive means being non-cyclic.As we can see from its definition,the classical structural equation causal model is deterministic and unable to deal with uncertainty and probability.

On the other hand,there has been extensive study about the probabilistic features of causal Bayesian network.However,as argued by Pearl in[10],a pure causal Bayesian network is insufficient to provide a complete account of causal reasoning for counterfactuals (the causal Bayesian network is at a lower level than structural equation models in the so called“causal hierarchy”).

Causal reasoning with counterfactuals in a non-deterministic or probabilistic situation is very natural in the real life.For instance,it is natural to infer from“It is very probable that the the heat is off”and“Had the heat been off,then it is very probable that the water pipes would been frozen this winter” to “It is very probable that the water pipes would been frozen this winter”.Therefore it calls for a logical analysis of probabilistic causal reasoning with counterfactuals.

1.2 Toward a qualitative analysis of probabilistic causal reasoning

In [7],Ibeling and Icard synthesize the previous study of deterministic causal models and probabilistic logic,and present a logical framework for probabilistic causal reasoning.They propose a semantics based on structural equation models extended with an additional partP,which is a probabilistic distribution over the valuation of exogenous variables.

The probability of propositions in such a model is defined in the following way:the probability ofφin a model(F,P)is defined as the probability of the setting of exogenous variables supportsφunderF.2Formally P(φ):=P({ ∈Σ|F, |=φ}).This can be seen as a“Laplacian”interpretation of probability: though the causal rules in the world is deterministic,there are still some unknown exogenous factors,which lead to the ignorance of their actual causal effects.Thus the uncertainty of a proposition (including any uncertainty of counterfactuals)can be reduced into the uncertainty of exogenous variables.

The logical framework proposed in [7] is quantitative.Its language needs to express the value of the probability assigned to a proposition.In addition,it has to include all the polynomial terms of the formt+t,t×t,-tin the object language.For instance,P(φ)+P(ψ)+1 is a polynomial term in the object language expressing the sum of the probability ofφand the probability ofψplus 1.

In this paper,on the contrary,I want to propose a qualitative logical framework instead of a quantitative framework,whose language does not involve any specific value of probability.In the procedure of causal reasoning,an agent does not necessarily involve any precise value of probability.For instance in the water pipe example above,to make the reasoning go through,it is sufficient to qualitatively know that the probability of certain propositions is almost 1,without knowing any quantity.

2 Qualitative Representation of Probabilistic Space

Similar to the quantitative account of probabilistic causal reasoning,my qualitative model consists of two parts: one part is the qualitative representation of causal effect,the other is the qualitative representation of the probabilistic distribution over variables.I also adopt the Laplacian treatment of uncertainty as[7]which reduces the uncertainty of causal effects into the uncertainty of the value of variables.Therefore the causal effect is still deterministic and can be represented by structural equations in the classical way as in[6,10].So we only need to looking for a qualitative representation of probabilistic distribution.

In[2],Baltag and Smets adopts the Popper-Renyi theory of conditional probabilities originated from[11,12](later developed by[4,5]),and proposed a qualitative representation of conditional probabilistic space.

Definition 1(Discrete Conditional Probabilistic Space).A pair (S,μ) withSis a finite set of states andμ:℘(S)×℘(S)→[0,1]satisfying:3℘(S)is the power set of S.

·μ(A|A)=1

·μ(A ∪B|C)=μ(A|C)+μ(B|C),ifA ∩B=Ø,CØ

·μ(A ∩B|C)=μ(A|B ∩C)·μ(B|C)

μis known as the discrete Popper function.SinceSis assumed to be finite,the functionμis completely characterized by the behavior on pairs of states(s,t)μ(reads thepriority degreeofswith respect tot)defined by:

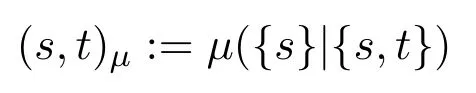
According to[2],μ(A|B)=1 can be interpreted asAis almost certain givenB,andμ(A|B)=0 can be interpreted asAis almost impossible givenB.

Given a probabilistic distribution characterised by a discrete probabilistic space,it is natural to assume an agent has a conditional beliefBP Q(reads“believeQconditional onP”)whenever the possibility ofQis almost certain givenP.In other words,BP Qiffμ(Q|P)=1,as proposed in[2].

Inspired by [5],[2] presents a qualitative description of a discrete conditional probabilistic space which only concern those probabilities that are equal to 1 or 0(which is enough for the evaluation of beliefs).The qualitative model is based on a notion called priority relation which is defined as:

Just as the priority degree completely characterizes a discrete Popper functionμon a finite space,the priority degree qualitatively characterizes the space in the sense that,for any pair of propositions,it tells whether the conditional probability is 1 or 0,as shown by the following theorem: ([1])

Theorem 1.Let(S,μ)be a discrete conditional probabilistic space and ≤μ be the priority relation derived from μ according to(*).For any X,Y ∈℘(S),μ(X|Y)=1iff all states in X is minimal with respect to ≤μ in Y.

Although the qualitative description only encodes a small part of the information carried by the quantitative model of probabilistic distribution,yet it is still powerful in the analysis of many important notions.For instance,it characterizes(conditional)belief in the following way: An agent believesPconditional onQif and only if min≤P ⊂Q,where min≤Pis the set of states that is minimal among theP-states with respect to≤μ.Unconditional belief can be defined as belief conditional on tautology.Baltag and Smets show that such a notion of belief based on discrete conditional probabilistic space can be characterized by conditional doxastic logic (CDL)in[1].

3 The Qualitative Logical Framework for Probabilistic Causal Reasoning

3.1 Embedding the plausibility relation into a causal model

In order to provide a qualitative account of probabilistic causal reasoning,I will embed the qualitative representation of probability proposed in[2]into a causal structure described by structural equation functions of variables.

Given a set of causal variablesU ∪V,the probabilistic distribution over variables can be represented by a probabilistic distribution over assignments.An assignmentAtoU ∪Vis a function fromU ∪Vto Σ,and for eachX ∈U ∪V,A(X)refers to the value assigned byA.The probabilistic distribution over the value of variables can be defined in terms of a probabilistic space(S,μ)whose states are all possible assignments toU ∪V,and the probability ofX=xconditional onY=ycan be defined as the value ofμ({A ∈S|A(X)=x} | {A ∈S|A(Y)=y})in a conditional probabilistic space.Particularly,in a causal scenario,Sare those assignments that comply with the causal rules.For convenience,I denote the set of all possible assignments that complies with a set of structural functionsFbyWF,which is formally defined as{A ∈ΣU∪V |∀X ∈V,A(X)=fX((A)-X)}.4I denote the sub-assignment of A to U ∪V {X}by(A)-X,if A is an assignment to U ∪V.

Then,by applying the approach in [2],such a conditional probabilistic space(WF,μ) can be qualitatively represented by a plausibility model〈WF,≤μ〉where the priority relation qualitatively representsμby the bi-condition:μ(X|Y)=1 iff all states inXis minimal with respect to≤μinY.

Therefore I propose the following model as a combination of the structural equation causal model and plausibility model.

Definition 2.A causal plausibility model is a tupleM=〈S,F,≤,A〉

·S=(U,V,Σ)is the signature whereUis the set of exogenous variables,Vis the set of endogenous variables,Σ is the range of those variables.

·Fis the set of structural functions,which is assumed to be recursive.

·≤is a total order overWF(namely all possible assignments that complies withF).

·Ais an assignment toU ∪Vthat complies withF,namelyA ∈WF

3.2 Syntax and semantics based on the new model

The formal language to talk about a causal plausibility model based on the signatureSis defined as below.

Definition 3(Language for Qualitative Probabilistic Causal Reasoning).LetS=(U,V,Σ),formulasφof the languageL(S)are given by5Bφ is seen as the abbreviation of B⊤φ.

whereX ∈U∪V,x ∈Σ andis a sequence of the formV1=v1,...,Vn=vnwhere∈V.6For convenience,I will write both V1= v1,...,Vn= vn and V1= v1 ∧··· ∧Vn= vn as=.

The languageL(S) is a combination of the language of conditional doxastic logic and the logic for causal reasoning.It not only contains the doxastic operatorB(which stands for belief) but also has the intervention operatorwhich stands for the antecedent of a counterfactual.

I will define the semantics of counterfactual based on the extended model under the classical interventionist interpretation: a counterfactualφholds on a modelMwheneverφholds on the modelwhich results from setting the value ofto.

Therefore,I will first define the notion of intervention on the causal plausibility model,as below.

Definition 4(Intervention).LetM=〈S,F,≤,A〉be a causal plausibility model；letbe a(possibly partial)assignment on the endogenous variables.The causal plausibility model,resulting from an intervention setting the values ofto(whereare endogenous variables),is defined as follows:

· the functions inare such that: for eachV not in,the functionis exactly asfV,and for each,the functionis aconstantfunction returning the valueregardless of the values of all other variables.

·is the unique solution towhose assignment to exogenous variables is identical withA.7Since F is recursive, is also recursive.Thus has unique solution with respect to each setting of exogenous variables.Formally,is the unique assignment that satisfies the following equations:

·is the unique assignment satisfyingwheneverA ≤AF.8is well-defined because F is recursive,so that there is a bijective mapping from WF and.

This definition of causal model results from an intervention is exactly in line with the traditional definition of intervention developed in[6]and[3].

Based on the definition of intervention on causal plausibility models,the semantics ofL(S)is given as below:

Definition 5.Semantics ofL(S)

·〈S,F,≤,A〉|=X=xiffA(X)=x

·〈S,F,≤,A〉 |=Bψφiff min≤||ψ|| ⊂||φ||,where||φ||:={A′ ∈WF |〈S,F,≤,A′〉|=φ}

·〈S,F,≤,A〉|=[-→X=-→x]φiff

· the Boolean connectives are defined in the usual way.

Given the semantics above,a logic for qualitative probabilistic causal reasoning can be derived from the syntax and semantics above.I denote all the valid formulas ofL(S)byLCP(S).In this paper,I will not discuss the axiomatization ofLCP(S).The idea of building the axiom system seems to be a combination of all the axioms in conditional doxastic logic as in[2]and the logic of counterfactuals in[6].However,such a logic system is not just a simple sum of the axioms of CDL and the logic of counterfactuals.For instance,andBφare both valid according to my semantics while it cannot be derived simply using the axioms of CDL and the logic of counterfactuals.Therefore the axiomatization forLCP(S) is still an open question worth investigation in the future.

4 Further Discussion

4.1 Qualitative independence

In probability theory,the quantitative representation of(conditional)probability gives rise to a quantitative notion of(conditional)independence.Letμbe a probabilistic distribution andX,Ybe two variables,the independence betweenXandYcan be defined in terms of the equation between unconditional probability and conditional probability,that is:Xis independent ofYwith respect toμwhenever for any valuex,y,μ(X=x)=μ(X=x|Y=y),as far asμ(Y=y)0.

Similarly,based on my causal plausibility model,the qualitative independence can be defined in terms of the equivalence between unconditional belief and conditional belief,that is:Xis qualitatively independent ofYwith respect toMwhenever for any valuex,y,M |=B(X=x)⇔M |=BY=y(X=x),as far asM |=¬BY=y⊥.

We can also generalize this idea to conditional independence.Xis probabilistically independent ofYconditional onZwith respect toμ,can be defined by: For anyx,y,z,μ(X=x | Y=y,Z=z)=μ(X=x | Z=z)as far asμ(Y=y,Z=z)0.Therefore,Xis qualitatively independent ofYconditional onZwith respect toMcan be defined by:M |=BY=y,Z=z(X=x)↔BY=y(X=x) as far asM |=¬BY=y,Z=z⊥.

Therefore,the syntax and semantics given in this paper enable us to derive a qualitative notion of independence in the same way as the quantitative notion of independence is derived from the probability.

4.2 Strengthen the connection between causality and probability in the model

The matching between causal structure and probability is an important aspect in the studies of causality.For instance the Markovian relativity and the“d-separation”criteria developed in[13]are core concepts in the study of causal Bayesian networks.

So far as I define the causal plausibility model in Section 3,there is only a weak connection between causality and probability: that is,only states that comply with the causal rules are considered as possible.It guarantees some obvious connection between causality and probability,for instance ifare all those variables other thanY,thenimplies(which means the probability ofY=yconditional onis 1).However such a connection is still weak that is unable to derive certain features that are intuitively right in the process of causal reasoning,as in the following example.

Example 1.John needs to catch up a flight at the airport tomorrow morning.If John gets up late or there is a traffic jam on the road to the airport next morning,then it is very probable that John will miss the flight.If John does not set any alarm clock in advance,then John probably gets up late.

The causal structure of this example can be graphically represented as below:

In this scenario,the following statements are intuitively right:

· (i)Given that John gets up early or not,the probability/belief of John missing the flight is independent of whether John sets up any alarm clock in advance.

· (ii)The probability/belief of there is a traffic jam on the road is independent of whether John sets up any alarm clock in advance.

As the qualitative independence can be expressed byL(S),if the causal reasoning of an agent about this scenario is properly modelled by a causal plausibility modelM,then this properties should be reflected by the formulas of this language.For instance,according to the analysis in section 4.1,property(i)can be expressed by the truth of the following formula:

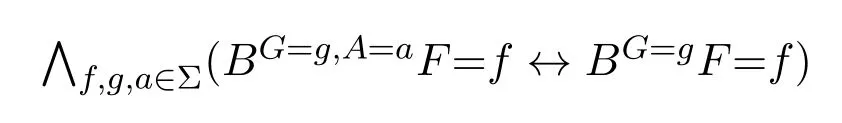
From the perspective of causal Bayesian nets,feature(i)and(ii)is guaranteed by the d-separation criteria: if assume the probabilistic distribution to be Markovian relative to the causal graph,thenAandFmust be independent conditional onGas they are d-separated by{G}.For the same reason,TandAare independent as they are d-separated byØ.Unfortunately,Definition 4 is unable to guarantee such kind of properties in a qualitative sense: for instance,it could be the case that for some≤overWF,those most plausibleG=0∧A=1-worlds are allF=1 worlds while some most plausibleG=0-worlds areF=0-worlds,so thatM |=BG=0,A=1F=1 butM |=¬BG=0F=1.This means an agent changes her mind aboutFby learning fromAeven if the information aboutGis given.This is not inconsistent,of course,if we take≤as some qualitative representation of the subjective belief about the external world.However if we want the agent to be more rational,then the possibility of such kind of belief revision should be ruled out.

In order to make≤more objective,≤should not be too arbitrary.Therefore some proper restrictions should be imposed on≤with respect toF.For instance,a natural restriction is that all exogenous variables should be independent.

If we assume the causal plausibility models modelling Example 1 must keep the independence of exogenous variables,then it exactly has the desired dependence and independence.In order to illustrate how this assumption works,let us take independence betweenF=1 andA=1 conditional onG=0 as an example:

M |=BG=0∧A=1F=1 iff min≤||G=0∧A=1||⊂||F=1||9||φ||={A ∈WF|〈S,F,≤,A〉|=φ}.

iff min≤||G=0∧A=1||⊂||G=0∧A=1∧F=1||

iff min≤||UA=1||⊂||UA=1∧UT=1∧UE=1||

iff min≤||UA=1∨UG=0||⊂||(UA=1∨UG=0)∧UT=1∧UE=1||(by the assumption

thatMkeeps the independence of exogenous variable)

iff min≤||G=0||⊂||G=0∧F=1||iff min≤||G=0||⊂||F=1||

iffBG=0F=1

This result fits our intuition: given John does not get up late,then whether the alarm is set will be irrelevant to whether John misses the flight.

Therefore,based on the same syntax and semantics as in section 3.2,the logic with respect to causal plausibility models that keep the independence of exogenous variables is also useful in the qualitative analysis of dependence and independence.

5 Conclusion

In this paper,I proposed a qualitative model of probabilistic causal reasoning called causal plausibility model.Based on the method of[2],the plausibility relation in this model can be seen as a qualitative representation of the probabilistic distribution over causal variables.I also proposed a syntax and semantics to describe the model from a logical perspective.In addition,the formal language is able to express a qualitative notion of dependence among causal variables in terms of epistemic operators.I also showed that by imposing certain restrictions on the plausibility ordering of the causal plausibility model,the qualitative logical framework can also be used to analyse the dependence and independence among variables in a causal graph.