并网逆变器三矢量模型预测直接功率控制
何潜, 何攻, 陈力, 帅红, 孙越
1. 国网重庆市电力公司,重庆 400015; 2. 重庆大学 电气工程学院,重庆 400044
分布式能源以分散型、 小规模的方式在用户旁就近布置,能够独立输送能源,与大电网等集中型能源供应方式相比,其能源利用率高,对环境友好,故越来越受到人们关注[1-4].而困扰分布式能源发展的重要因素为并网问题,为将其更高效地应用,并网逆变器作为将能源输入电网的核心装备受到学者们重视,并网逆变器控制性能直接关系并网电能质量,多年来对其控制策略的改进一直是研究热点.模型预测直接功率控制(Model Predictive Direct Power Control,MPDPC)逻辑简单,动态响应快,价值函数设计灵活,能够较好地处理系统非线性约束.MPDPC与传统直接功率控制相比,不仅无需繁琐的PI参数设计,而且通过功率预测模型选择最优开关矢量,解决了传统直接功率控制由启发式开关表选取矢量的不精确性问题[5-6].
目前单矢量模型预测控制应用较为广泛,虽然该控制策略有诸多优点,但其输出电压矢量直接在7种基本电压矢量中选取,方向与幅值均不可调,且在单个控制周期内仅作用一个电压矢量,控制精度有待提高[7-8].对于以上问题,可以采用在单个控制周期内增加作用的电压矢量数目来解决.双矢量模型预测控制是在单矢量预测控制的基础上增加了一个电压矢量[9-11],占空比模型预测控制是双矢量模型预测控制的一种,该控制策略将一个有效电压矢量与零电压矢量进行组合作用在当前控制周期,其中第二个电压矢量固定为零电压矢量,故在每个控制周期中只可选择6个固定方向的电压矢量[12-14].文献[15-16]提出的双矢量模型预测控制没有特别规定某一电压矢量为零电压矢量,并在分配两个电压矢量的作用时间时遵循无差拍控制的方式,其输出电压矢量的覆盖范围在一定程度上得到了扩大,但当两个电压矢量均为有效电压矢量时,其输出电压矢量的幅值不可调,使输出电压矢量覆盖范围仍受限.针对双矢量模型预测控制的局限性,本文在其基础上又增加了一个电压矢量作用在每个控制周期,提出一种基于并网逆变器的三矢量模型预测直接功率控制,先通过价值函数从6个有效矢量中优选出第一个电压矢量,然后将其余5个有效矢量连同零矢量合成出5个期望电压矢量,使输出电压矢量的方向与幅值均可调,且通过功率无差拍原则分配电压矢量作用时间,同时完成了对有功功率与无功功率的无差拍控制,提高了控制精度.最后,由仿真与实验结果证实了所提三矢量MPDPC的可行性和有效性.
1 并网逆变器离散数学模型
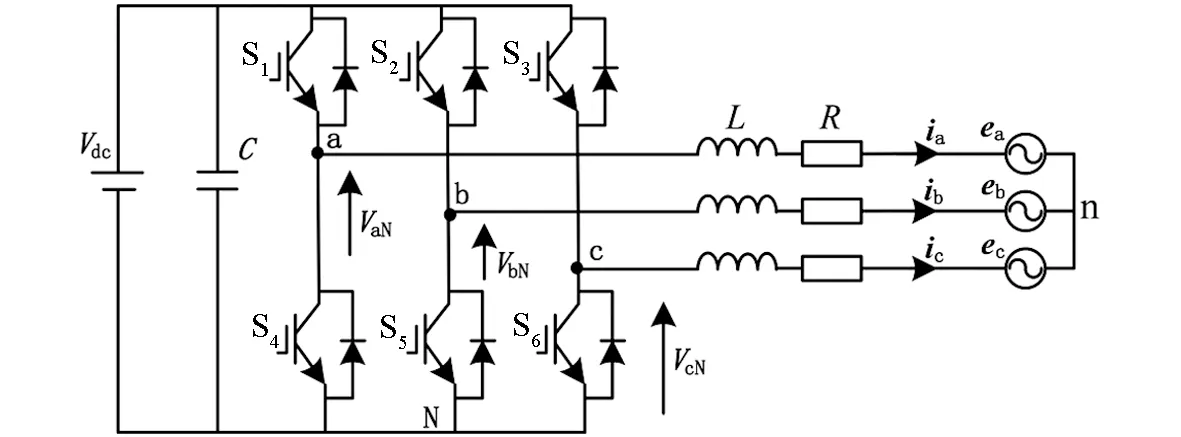
图1 电压源型PWM并网逆变器拓扑结构
电压源型PWM并网逆变器的拓扑结构如图1所示,其中,Vdc、C分别为直流侧的电压、 电容,S1至S6分别为并网逆变器内部的6个开关器件,L,R分别为滤波电感、 线路电阻,ia,ib和ic分别为逆变器网侧三相电流,ea,eb和ec分别为逆变器网侧三相电压,n为网侧中性点,VaN,VbN和VcN分别为逆变器三相的输出电压.由于逆变器处在任何一种工作状态下,其每项桥臂仅允许一个开关器件导通,因此上下开关器件的状态应该互补,可设Si为单极性二值逻辑开关函数,上桥臂导通可表示为Si=1,下桥臂导通可表示为Si=0,i为a,b,c.
并网逆变器在两相静止(αβ)下的数学模型可表示为
(1)
式(1)中eα,eβ,iα,iβ分别为电网电压与网侧电流在αβ坐标系下的分量;uα,uβ为逆变器输出电压在αβ坐标系下的分量,可表示为
(2)
由式(1)可得:
(3)
由瞬时功率理论,可将有功功率p与无功功率q表示为
(4)
对式(4)两边同时求导可得:
(5)
将式(3)代入式(5)有:
(6)
根据欧拉法,由式(6)可得并网逆变器在两相静止坐标系下的离散功率预测模型:
(7)
式(7)中k表示时间离散化后的当前时刻,k+1表示下一时刻.
2 模型预测直接功率控制
2.1 单矢量模型预测直接功率控制
单矢量MPDPC输出的最优电压矢量uopt直接从7种基本电压矢量中选取,其电压矢量选择如图2所示.
单矢量MPDPC的思路为根据瞬时功率理论,由在两相静止坐标系下的当前时刻电压和电流计算出当前时刻功率,通过功率预测模型预测下一时刻功率.其中价值函数根据功率给定值与功率预测值间的误差最小来设计,使价值函数g最小的电压矢量即为最优电压矢量.
g=|p*-p(k+1)|+|q*-q(k+1)|
(8)
式(8)中p*,q*为有功功率与无功功率的给定值.
2.2 双矢量模型预测直接功率控制
双矢量MPDPC在单矢量MPDPC的基础上,增加了一个电压矢量作用在每个控制周期,其电压矢量选择如图3所示,第一个电压矢量用u1表示,其作用的时间为t1,第二个电压矢量用u2表示,其作用的时间为t2.

图2 单矢量MPDPC矢量选择

图3 双矢量MPDPC矢量选择
根据无差拍控制原则,可将下一时刻的无功功率表示为
q(k+1)=q(k)+sq1t1+sq2(Ts-t1)=q*
(9)
式(9)中sq1为在第一个电压矢量作用下的无功功率斜率;sq2为在第二个电压矢量作用下的无功功率斜率.由式(6)可得:
(10)
(11)
(12)
式(10)-(12)中uz为零电压矢量,sqz为在零电压矢量作用下的无功功率斜率;uα1,uβ1,uα2,uβ2分别为第一个电压矢量与第二个电压矢量在αβ坐标系下的分量.
由式(9)可得第一个电压矢量与第二个电压矢量各自的作用时间分别为
(13)
t2=Ts-t1
(14)
双矢量模型预测直接功率控制的输出电压矢量在由第一个电压矢量与第二个电压矢量合成的期望电压矢量中选取,此时式(7)中的uα,uβ可表示为
(15)
(16)
双矢量模型预测直接功率控制先从7种基本电压矢量中通过价值函数选取第一个最优电压矢量,然后将其余6种电压矢量作为与第一个最优电压矢量合成期望电压矢量的备选.最后将使g最小的期望电压矢量输出,其相应所选的备选矢量即为第二个电压矢量.
3 三矢量模型预测直接功率控制
3.1 基本原理

图4 三矢量MPDPC矢量选择
为使功率预测值进一步逼近功率给定值,并同时对有功功率与无功功率完成无差拍控制,提高系统性能,本文在双矢量模型预测直接功率控制的基础上在每个控制周期内再增加一个起作用的电压矢量,提出一种三矢量模型预测直接功率控制策略,该策略通过两个有效电压矢量与一个零电压矢量合成出期望电压矢量作用在每个控制周期,其电压矢量选择见图4.
该策略先在6种有效电压矢量中通过价值函数优选出第一个电压矢量,再将剩下5种有效电压矢量作为备选矢量与第一个电压矢量连同零电压矢量各自组合,合成出5种期望电压矢量,将使g最小的期望电压矢量输出,其输出电压矢量方向与幅值均可调.并网逆变器三矢量模型预测直接功率控制的系统控制框图见图5.

图5 并网逆变器三矢量MPDPC系统控制框图
3.2 矢量作用时间
根据无差拍控制原则,可将下一时刻的有功功率、 无功功率表示为
(17)
式(17)中sp1,sp2,spz分别为在第一个电压矢量、 第二个电压矢量、 零电压矢量作用下有功功率的斜率,tz表示零电压矢量作用的时间.
(18)
(19)
(20)
联立式(10)-(12)、 式(17)-(20)可得到各矢量的作用时间:
(21)
tz=Ts-t1-t2
在计算出3个电压矢量的作用时间后,还需要考虑其数值是否在0~Ts范围内,可分如下4种情况:
1) 若t1,t2和tz均在0~Ts范围内,则让两个有效矢量与一个零矢量作用于当前控制周期.
2) 若t1和t2均在0~Ts范围内,且tz未在0~Ts范围内,则让两个有效矢量作用于当前控制周期.
3) 若t1和t2中仅一个在0~Ts范围内,且tz在0~Ts范围内,则让一个有效矢量与一个零矢量作用于当前控制周期.
4) 若t1和t2中仅一个在0~Ts范围内,且tz未在0~Ts范围内,则让一个有效矢量作用于当前控制周期.
3.3 电压矢量的合成
三矢量模型预测直接功率控制通过两个有效电压矢量与一个零电压矢量来合成期望电压矢量,三矢量模型预测直接功率控制的电压矢量选择如表1所示,期望电压矢量uexp的合成如图6所示.

表1 三矢量模型预测直接功率控制矢量选择

图6 三矢量期望电压矢量合成
基于三矢量的模型预测直接功率控制策略实现如下:
1) 根据单矢量模型预测直接功率控制策略选取第一个电压矢量.
2) 根据式(10)-(12)、 式(17)-(20)计算功率斜率,并由式(21)得到3个矢量的作用时间,并分情况考虑其范围.
3) 由式(15)、 式(16)得到6种期望电压矢量在两相静止坐标系下相应的分量,并将其代入式(7)得到对应的有功、 无功功率预测值.
4) 将预测的功率值代入式(8),选择令g最小的期望电压矢量输出至空间矢量脉宽调制模块.
4 3种控制策略的比较
根据上述3种模型预测直接功率控制策略的原理,表2对比了其矢量数目、 寻优计算和电压矢量作用时间计算方法,由该表可知,相比双矢量法在单个控制周期内需要13次寻优且仅对无功功率完成无差拍控制,三矢量法则减少了寻优次数,降低了计算量,并通过有功功率和无功功率无差拍控制的方式来计算电压矢量的作用时间,同时实现了对有功功率与无功功率的无差拍控制,可以取得更好的控制效果.

表2 3种控制策略的比较
5 仿真与实验结果分析
对单矢量、 双矢量、 三矢量模型预测直接功率控制这3种控制策略在Matlab/Simulink中搭建了相应的仿真模型进行比较分析.并网逆变器参数见表3.

表3 并网逆变器参数
5.1 仿真结果分析
并网逆变器在3种模型预测直接功率控制下的稳态网侧三相电流波形如图7所示.相比单、 双矢量模型预测直接功率控制,在本文所提三矢量法控制下,网侧三相电流波形更平滑、 正弦度更好.
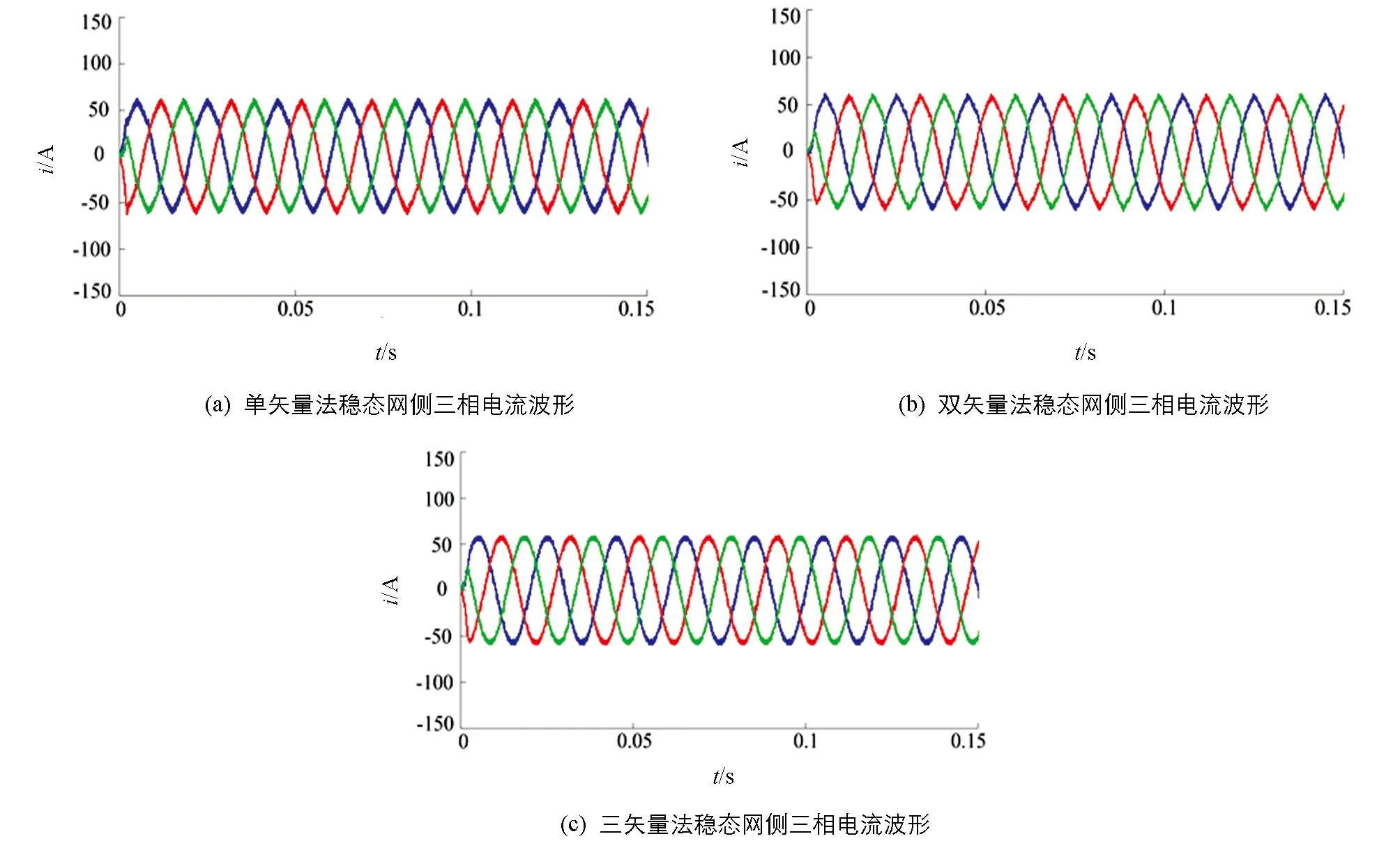
图7 3种控制方法的稳态网侧三相电流波形
在0.2 s时将p*从25 kW突变到50 kW.由图8可见,在3种控制方法下的p都能快速响应p*的改变,动态性能较好,其中双矢量法由于对无功功率实现了无差拍控制,故无功功率脉动相比单矢量法有所改善,但有功功率脉动仍较大.相比单矢量和双矢量法,三矢量法同时对有功、 无功功率实现了无差拍控制,较好地改善了功率脉动,提高了控制精度.

图8 功率突变下3种控制方法的功率响应
图9为3种控制方法的网侧A相电流动态波形,其均可快速响应p*的突变,具有较好的动态性能.在逆变器采用单、 双矢量法控制时,电流均存在较明显畸变,在逆变器采用三矢量法控制时,电流波形平滑,正弦度较高,波形质量得到较好改善.
图10为3种控制方法的A相电流谐波畸变率,其均小于5%,满足逆变器电流并网的国家标准.相比单、 双矢量模型预测直接功率控制,三矢量法的电流谐波畸变率更低,进一步改善了并网电能质量.
5.2 实验结果分析
为进一步验证三矢量模型预测直接功率控制相比单、 双矢量模型预测直接功率控制更有效,本文基于RT-LAB半实物仿真系统搭建了并网逆变器实验平台,实验与仿真的并网逆变器参数一致.
由图11可见,相比单、 双矢量模型预测直接功率控制,三矢量法在有功功率给定值发生突变前后,网侧三相电流正弦度更高,具有较好的波形质量.
由图12可见,三矢量模型预测直接功率控制的电网电压与网侧A相电流几乎同相位,功率因数较高,且在有功功率给定值突变后能迅速响应,相比单、 双矢量模型预测直接功率控制波形更平滑、 控制效果更好.
综上所述,相比于单、 双矢量模型预测直接功率控制,本文所提三矢量模型预测直接功率控制具有更好的控制性能,实验结果验证了仿真与理论的有效性.

图9 功率突变下3种控制方法的A相并网电流动态波形
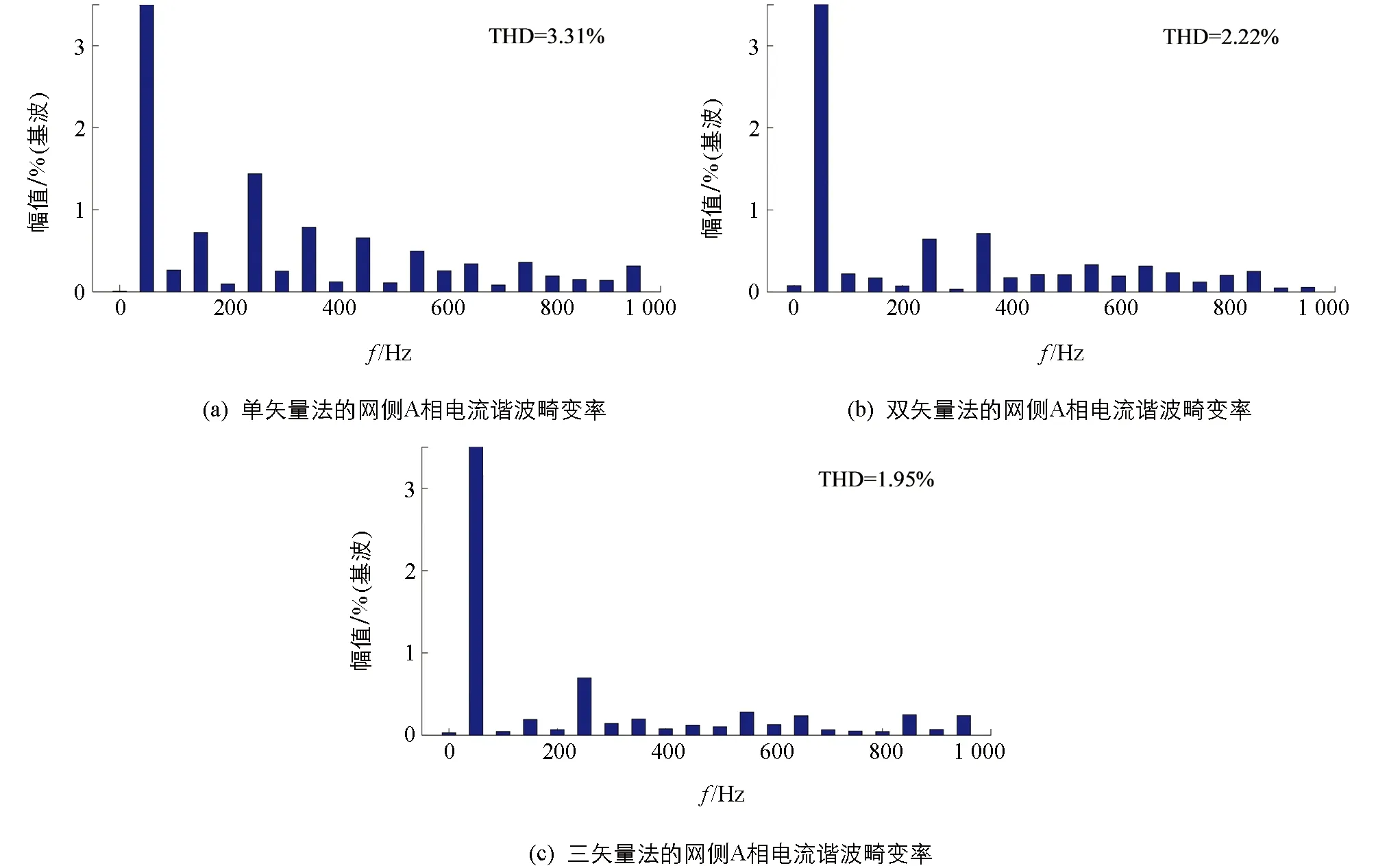
图10 3种控制方法的网侧A相电流谐波畸变率

图11 功率突变下3种方法的三相并网电流

图12 功率突变下3种方法的电网电压与网侧A相电流
6 结论
本文将并网逆变器作为研究对象,在传统单矢量模型预测直接功率控制的基础上引入双矢量模型预测直接功率控制,并针对双矢量法的局限性提出了一种三矢量模型预测直接功率控制策略.本文所提三矢量模型预测直接功率控制先在6个有效矢量中优选第一个矢量,再将其与余下5个有效矢量连同零矢量合成期望电压矢量,使输出电压矢量的幅值与方向均可调,并同时对有功、 无功功率实现了无差拍控制,提高了功率控制精度.仿真与实验结果表明: 相比于前两种控制方法,本文所提三矢量模型预测直接功率控制能较好地提高逆变器网侧电流波形质量,降低电流谐波畸变率,改善功率脉动,具有良好的动态和稳态性能.

