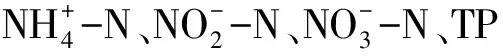基于HYDRUS-1D的改良土壤渗滤处理污废水模型研究

吕晶晶 石兰君 窦艳艳 龚为进 张列宇

(1.中原工学院,郑州 450007;2.河南省地质矿产勘查开发局第二地质环境调查院,郑州 450053;3.中国环境科学研究院,北京 100012)

污染物质在土壤渗滤系统中的迁移转化呈现一定的规律性，掌握水溶性污染物质运动及迁移转化的特点对土壤渗滤系统的设计、运行和维护意义重大。通过构建数学模型模拟可以从宏观上研判土壤渗滤系统的运行变化规律，有利于对土壤渗滤系统的进行系统和科学管理。

HYDRUS-1D是美国农业部联合其它相关机构在SUMATRA和WORM等模型的基础上研发而来的一种新的模型[1]。此模型可以在宏观与微观两种尺度上模拟一维水流、溶质等在饱和或者非饱和介质中的迁移转化[2]。此模型中方程求解运用的是Galerkin线性有限元的方法，可以用来模拟水及水中化学元素和有机污染物质的运移过程，因此，此模型被广泛应用于土壤学、环境学及水文地质学等领域[1]。本研究以前期碳、氮、磷等营养元素实验数据为基础，运用HYDRUS-1D模型揭示各污染物质在土壤渗滤系统中的运移规律。先前对HYDRUS-1D的研究和应用主要集中在包气带环境中，鉴于包气带环境与土壤渗滤系统的内部环境有相似之处，所以将HYDRUS-1D引入用来模拟土壤渗滤系统中水分及水溶性污染物质的运动及迁移转化。

在下面的模型建立过程中，根据实际情况对模型进行简化：(1)各层土壤都是均匀的；(2)污水下渗的过程中土壤内部结构及孔隙不变；(3)只考虑土壤中水及其污染物的的运移，而不考虑土壤中水汽的运动；(4)不考虑温度对反应的影响；(5)土壤中水分运动不考虑水平或侧向水流运动，而只考虑一维垂向运动；(6)不考虑大气对土壤中水流运动的影响。模型中时间的单位是d，距离单位是cm。

本文中试试验装置见图1、2。

图1 中试试验基地现场部分装置实物图片

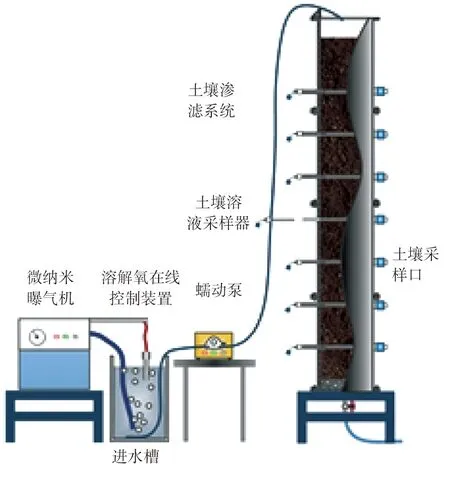
图2 中试试验装置示意图(前加曝气预处理)[3-4]

1 改良土壤渗滤模型建立

1.1 改良土壤渗滤水流模型

在变饱和孔隙介质中，HYDRUS-1D软件运用Richards方程表述一维平衡水流运动过程[5]，公式如下式所示：

(1)

公式当中各符号的含义为：θ代表体积含水率，单位是m3·m-3；t代表模拟时间，单位是d；x代表纵坐标垂直向下的距离，单位是m；h代表压力水头，单位是m；α代表水流方向与纵坐标轴的夹角，对于一维连续垂直入渗的水流此值为0°；S代表源汇项，即植物根系吸水量，单位是m3·m-3·a-1，对裸露区为0；K(h)代表非饱和渗透系数函数，可由方程K(h,x)=Ks(x)·Kr(h,x)计算得出，其中，Ks代表饱和渗透系数，单位是m·a-1，Kr代表相对渗透系数，无量纲。对于非饱和孔隙介质，上面公式中的参数θ和K与压力水头h都存在非线性关系，HYDRUS-1D软件中提供了5种模型来计算这些参数，这些模型包括Garder模型、Brooks-Corey模型、Garder-Russo模型、Campbell模型、Van Genuchten-Mualem模型等，本次研究选用目前使用最广泛、发展最成熟的van Genuchten-Mualem模型(简称为VG模型)来计算土壤水力特性参数θ(h)和K(h)，并且不考虑水流运动滞后的现象[6]。van Genuchten-Mualem模型是由1976年Mualem提出的统计孔径分布模型发展而来的，又在1980年由RienvanGenuchten提出以土壤水分特征参数函数的形式预测非饱和渗透系数的数学模型。VG模型的表达式如下：

(2)

(3)

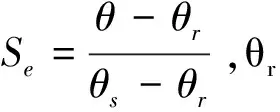
1.2 改良土壤渗滤污染物运移模型

HYDRUS-1D软件中采用对流-弥散方程来描述一维溶质的运移过程[8]。公式表达式如下式所示：

(4)

公式当中各符号的含义为：θ代表体积含水率，单位是m3·m-3；t代表模拟时间，单位是a；c代表溶质液相浓度，单位是g·m-3；s代表溶质固相浓度，单位是g·g-1；D代表弥散系数，表示分子扩散和水力弥散，单位是m2·a-1；q代表体积流动通量密度，单位是m·a-1；Φ代表源汇项，表示水溶性物质发生的各种反应，单位是g·m-3·a-1。

1.3 模型的初始条件与边界条件

考虑到进水是连续的，并且在一定时间内流量恒定，所以水流上边界条件选择定水头边界，根据流量设定顶部水头为0.06m(即进水水力负荷6cm/d)，下边界条件为自由排水边界。

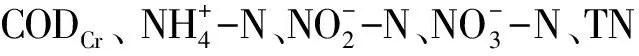
表1 土壤中CODCr迁移转化参数

表2 土壤中氨氮迁移转化参数

表3 土壤中TP迁移转化参数

2 数值模拟与参数识别

2.1 模型模拟

本模型用来模拟地面以下0～180cm深度范围的土壤，分为2层，模拟时间从2014年10月19日至12月10日，采用变化时间步长剖分的方式，根据收敛迭代次数调整时间步长。设定初始时间步长为0.1d，最小时间步长和最大时间步长分别为0.0ld和10d；土壤含水量和压力水头的容许偏差分别为0.0005和1cm。

土壤水流模型运用单孔隙模型中VG模型[10]，不考虑水流运动滞后的现象，采用逆向求解方法确定水中溶质运动的参数。水流模拟与污染物模拟上边界条件均为开放型大气边界，接受降水、灌溉等的水分补给和土面水分蒸发，HYDRUS-1D水流模拟模型赋以实际测得的降水量、灌溉量和蒸发量；盐分模拟赋以实际测得的灌溉水矿化度。水流模拟下边界条件为已知的变水头边界，HYDRUS-1D中赋以的压力水头，根据实际测得的地下水位埋深确定；污染物模拟下边界为已知浓度边界，赋以实际测得的污染物浓度平均值。

2.2 模型参数

土壤水力参数由实际测得的土壤粒径组成，根据Rosetta模型初始值赋以参数初始值[11]，而后根据试验实际测得的数据进行参数拟合，最终确定主要特征参数的数值，表4给出了调整之后的VG公式中各土壤水力参数的数值。

表4 土壤水力参数

2.3 模型验证与效果评价

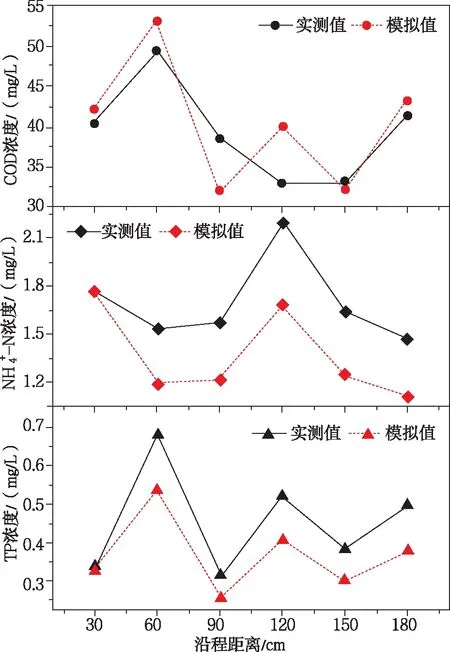
图3 不同点位出水浓度实测值与模拟值对比

3 模型应用与分析

对于已经建立并通过验证的模型主要应用在以下部分：方案一：边界条件中进水通量和浓度不变，土壤层高度为1.8m时，粉土/粉质黏土的厚度发生变化，对去除效果影响的模拟，从而得出粉土/粉质黏土厚度的最佳组合；方案二：边界条件中进水通量和浓度不变，土壤层高度为1.8m时，粉土和粉质黏土的装填次序、厚度发生变化对去除效果的模拟，从而得出污染物去除率最高时装填组合。

图4 模拟粉土/粉质黏土不同厚度组合出水水质指标

图5 模拟粉质黏土/粉土不同厚度组合出水水质指标

4 小结

(1)水流上边界条件选择定水头边界0.06 m，下边界条件为自由排水边界。污染物运移的边界条件以液相溶质浓度作为模型的初始条件，上边界条件选择定污染物浓度通量边界，下边界条件为零浓度梯度边界。根据对流-弥散方程，通过参数率定可以建立与实测值相关性良好的土壤渗滤处理污水模型。

(2)在参数率定阶段，发现对模拟结果影响最大的因素为溶质在反应相的反应速率常数μ，而弥散系数DL和吸附系数Kd对溶质运移模拟结果的影响小于μ的影响。