等同现浇的装配式钢筋混凝土剪力墙抗弯承载力可靠度分析

郭圣祈，汪梦甫

（湖南大学土木工程学院，湖南 长沙 410082）

引言

目前，我国规范JGJ 1－2014《装配式混凝土结构技术规程》［1］中关于“等同现浇”的装配式剪力墙的结构、构件设计建议为“可按现行行业标准JGJ 3－2010《高层建筑混凝土结构技术规程》［2］有关规定进行结构抗震性能设计”及“装配式结构构件及节点应进行承载能力极限状态和正常使用极限状态设计，并应符合国家标准GB 50010－2010《混凝土结构设计规范》［3］等的有关规定”，即建议对连接性能良好的的装配式剪力墙采用等同现浇的方法进行设计。然而，虽然“等同现浇”的装配式钢筋混凝土剪力墙在一定程度上与现浇钢筋混凝土剪力墙抗震性能相近，但两者承载能力存在一定程度的偏差。我国GB 50068－2001《建筑结构可靠度设计统一标准》［4］对砌体结构、钢结构、钢筋混凝土结构及木结构等不同类型构件的承载能力可靠指标进行了较系统的计算，但并未对采用规范中现浇剪力墙抗弯承载力设计公式进行“等同现浇”的装配式剪力墙抗弯承载力设计的可靠度进行论证，因此很有必要对其进行可靠度分析。

基于此，文中以等同现浇的装配式钢筋混凝土剪力墙为研究对象，收集并整理了国内“等同现浇”装配式钢筋混凝土矩形截面剪力墙（以下简称“装配式剪力墙”）试验数据，并基于统计分析确定抗弯承载力计算模式的不定性统计参数，随后充分考虑几何参数、材料参数及计算模式不确定性情况下，以建立的功能函数对装配式剪力墙采用规范［2－3］中抗弯承载力设计公式的可靠指标进行计算，同时进行可靠指标影响因素分析，并基于目标可靠指标对抗弯承载力设计公式提出相应的修正建议。

1 规范中现浇钢筋混凝土剪力墙抗弯承载力设计公式

文中主要是对装配式钢筋混凝土矩形截面剪力墙采用规范［2－3］中抗弯承载力设计公式的可靠度分析，因此对规范［2－3］中抗弯承载力公式进行处理，获得现浇钢筋混凝土矩形截面剪力墙（以下简称“现浇剪力墙”）抗弯承载力F计算公式为：

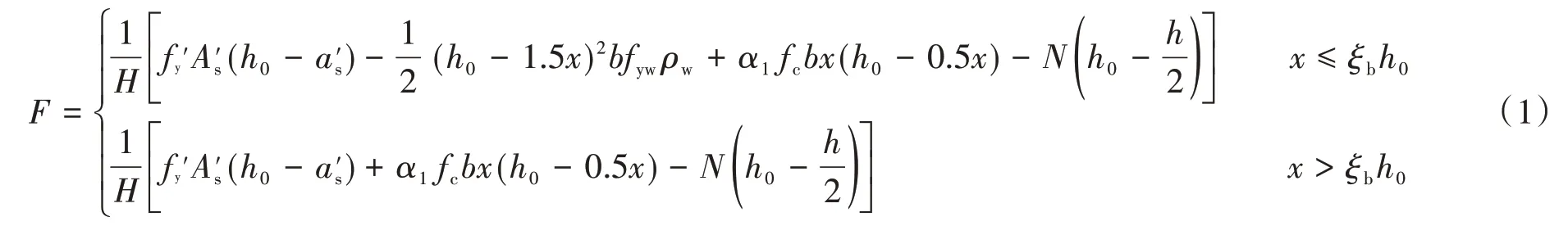
式中，

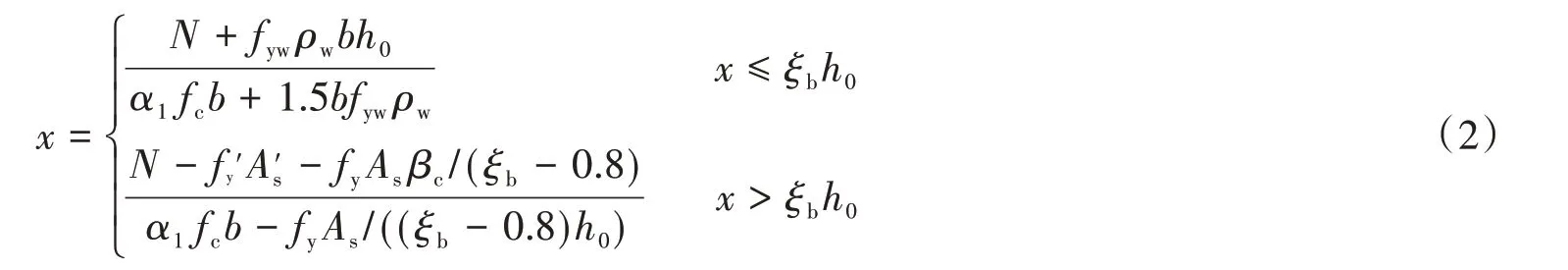
式中：A′s、f′y分别为墙体受压区的端部纵向钢筋的截面面积和抗拉强度设计值；As、fy分别为墙体受拉区的端部纵向钢筋的截面面积和抗拉强度设计值；ρw、fyw分别为墙体腹板纵向钢筋的配筋率和钢筋抗拉强度设计值；fc为混凝土轴向抗压强度设计值；H为剪力墙的高度；b、h分别为剪力墙矩形截面的宽和高；h0为截面的有效高度，取h0=h－a′s，a′s为墙体截面受压区端部钢筋的合力点与受压区外边缘之间的距离；a1为受压区混凝土矩形应力图的应力与混凝土轴心抗压强度的比值；βc混凝土强度影响系数；N为剪力墙轴向压力；x为剪力墙底部截面等效受压区高度；ξb为界限相对受压区高度。

根据规范［3］，剪力墙轴向压力N和界限相对受压区高度ξb可以通过式（3）、式（4）获得：

式中：n为剪力墙的轴压比；Es为墙体端部纵向钢筋弹性模量；εcu为混凝土极限压应变。

2 试验数据统计与分析

2.1 试验数据统计

通过对国内装配式钢筋混凝土剪力墙试验数据进行收集和筛选，获取了96片装配式剪力墙试验结果作为文中分析的数据库，其数据来源见表1所示。文中所采用的试验结果对应剪力墙试件满足如下条件：（1）剪力墙试件均为矩形截面，且均为低周往复加载；（2）所选择的墙体不包含如钢－混凝土复合墙体、带暗支撑墙体、带洞口等非传统型剪力墙试件；（3）剪力墙试件为弯曲破坏或剪切效应相对较弱的弯剪破坏形态；（4）试验参数完整且试验成功，能满足分析需要的试件。

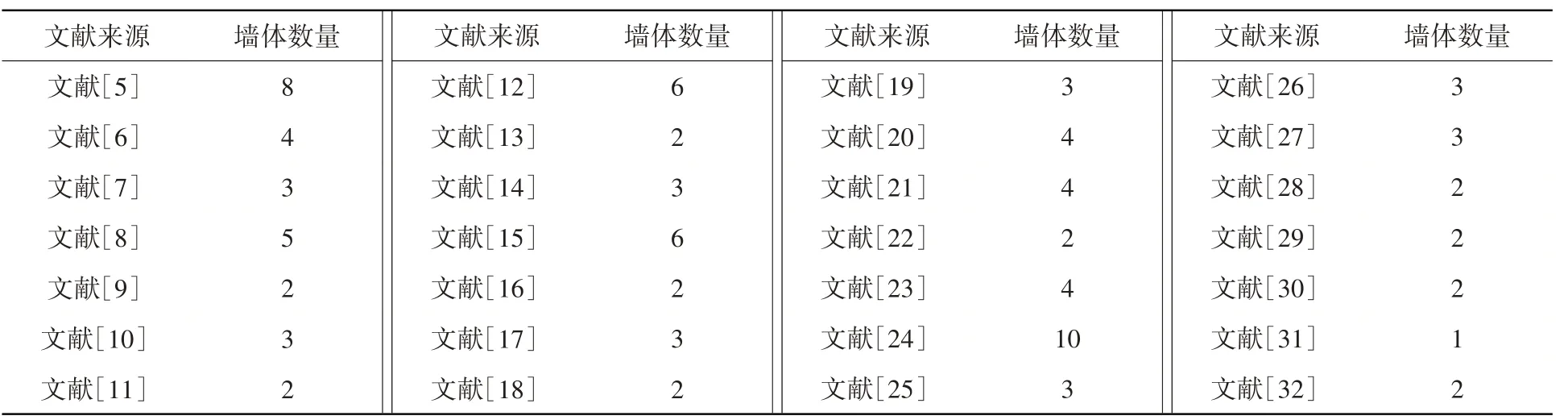
表1 试验数据统计Table 1 Statistics of experimental data

为了能更好地检测现浇剪力墙抗弯承载力公式对装配式剪力墙的计算准确度，将表1中所收集的符合筛选条件的96片进行如下方式分为3级6类处理：（1）第1级共1类，为全部96片墙体（记为Ⅰ类）；（2）第2级按照墙体剪跨比分2类，第1类为全部96片墙体中剪跨比≥2的墙体（记为Ⅱ类），第2类为全部96片墙体中剪跨比＜2的墙体（记为Ⅲ类）；（3）第3级按照装配节点连接方式分3类，第1类为套筒连接（包含套筒浆锚连接、套筒挤压连接等，记为Ⅳ类），第2类为搭接连接（包含预留孔洞浆锚搭接连接、约束浆锚搭接连接等，记为Ⅴ类），第3类为其它连接（包含螺栓连接、U型环扣连接等，记为Ⅵ类）。分级分类墙体数量见表2所示。

表2 分级分类墙体数量统计Table 2 Classified statistics of the number of walls

2.2 计算模式不确定性分析

装配式剪力墙采用规范中现浇剪力墙的抗弯承载力设计公式的计算模式不确定性可用随机变量KΩ来表示［4］，

式中：Ft为墙体抗弯承载力试验值；F为将收集到的各试件墙体相关参数代入式（1）～式（4）获得的墙体抗弯承载力计算值。需要说明的是，由于装配式剪力墙存在装配节点，而一般装配节点处的纵向钢筋配筋率会比预制部分的纵向钢筋配筋率大，为了保证式（5）中F值采用现浇剪力墙抗弯承载力计算公式进行计算的合理性，在进行计算时，统一采用预制部分的纵向钢筋配筋率进行计算。根据式（5）计算得到3级6类墙体抗弯承载力计算模式不确定性参数KΩ的统计参数见表3所示（统计分析中并无异常值出现）。

表3 计算模式不确定性参数KΩ的统计参数Table 3 Statistics of the calculation model uncertainty parameters KΩ

从整个数据库数据分析来看，装配式剪力墙试件试验值与规范抗弯承载力设计公式计算值之比为1.06，变异系数为0.109，这说明采用式（1）～式（4）进行的计算结果与试验结果拟合较好，即装配式剪力墙采用现浇剪力墙抗弯承载力设计公式具有较高的准确性。通过对比Ⅱ、Ⅲ类墙体的分析结果发现，式（1）～式（4）对剪跨比≥2的墙体墙体计算结果比剪跨比＜2的墙体计算结果更加准确。这主要是因为剪跨比＜2的墙体在低周往复加载过程中的体现出的剪切特性强于剪跨比≥2的墙体墙体，展现出更高的承载特性。通过对比Ⅳ、Ⅴ、Ⅵ类可以发现，式（1）～式（4）对采用套筒连接的墙体计算结果更加准确，而对搭接连接的墙体计算结果稍微偏小。这主要是因为，采用套筒连接的墙体连接性能更加贴近现浇墙体，因此计算结果与现浇墙体计算结果更加接近；搭接连接墙体在连接部位的双倍搭接钢筋面积增强了墙体的抗弯承载能力，而在采用式（1）～式（4）计算时，并未考虑双倍搭接钢筋面积对抗弯承载力的影响，因此其计算结果稍微偏小导致墙体抗弯承载力计算模式不确定性参数KΩ的均值偏大。

3 可靠度分析

3.1 几何参数的不确定性

钢筋混凝土剪力墙的几何参数不确定性是由各尺寸参数统计量的随机性导致，选取文献［33］中几何参数不定性变量的统计参数均值kl和变异系数δl见表4所示。

表4 几何尺寸统计参数Table 4 Statistical parameters of geometrical dimensions

3.2 材料参数的不确定性

材料参数的不确定性主要由材料本身品质、环境条件及制作工艺等差异导致。根据规范［4］规定，混凝土抗压强度及钢筋抗拉强度是影响钢筋混凝土剪力墙抗弯承载力的主要材料参数，两者均服从正态分布。

混凝土材料的轴心抗压强度不确定性若采用随机性变量Y进行表示，则可表示为：

式中：fc.t为结构构件的混凝土实际轴心抗压强度值；fck为试件混凝土轴心抗压强度标准值；fc.l为试件混凝土实际轴心抗压强度值。令f=fc.t/fc.l，则可求随机性变量Y的平均值μY为：

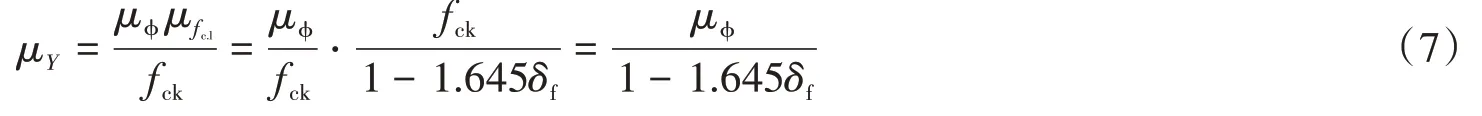
式中：μϕ为反映结构构件混凝土抗压性能与试件混凝土抗压性能的差别系数的均值，按照规范取μϕ=0.88；μfc.l为试件混凝土抗压性能fc.l的均值；δf为混凝土轴心抗压强度变异系数。根据我国规范［3］附录选取混凝土轴心抗压强度变异系数，并由式（7）求解混凝土材料的轴心抗压强度不确定性变量的均值μY见表5所示。

表5 混凝土轴心抗压强度统计参数Table 5 Statistical parameters of axial compressive strength of concrete

钢筋的统计参数均值kS与变异系数δS按照文献［33］取值，其统计参数见表6所示。

表6 钢筋强度统计参数Table 6 Statistical parameters of reinforcement strength

3.3 抗力统计参数计算与概率分布模型

根据我国规范［4］，剪力墙的抗弯承载力F可通过下式获得：

式中：fi、ai分别代表第i种材料的材料特性和几何特性；RP为根据随机变量fi、ai并采用式（1）～式（4）计算获得剪力墙的抗弯承载力。剪力墙的抗弯承载力F统计参数的均值kF和变异系数δF可通过下式求解：

式中：Fd为按照式（1）～式（4）求解的剪力墙抗弯承载力设计值。

由于抗力是由多个随机变量的乘积和形式构成，故统计分析时一般近似认为其服从对数正态分布［33］。

3.4 荷载统计参数与概率分布类型

根据GB50068－2001《建筑结构可靠度设计统一标准》［4］，永久荷载、楼面活荷载（住宅、办公）、风荷载的统计参数和概率分布类型见表7所示。

表7 荷载统计参数与概率分布类型Table 7 Statistical parameters and probability distribution types of loads

3.5 荷载效应组合

高层建筑中剪力墙所涉及的荷载类型包含永久荷载、楼面活荷载（住宅、办公）、风荷载，而我国规范［4］在对结构构件进行可靠度指标确定时所采用的3种荷载效应组合并未考虑风荷载与楼面活荷载同时出现的组合方式。因此，文中根据高层建筑中剪力墙的实际受力情况，在进行可靠度指标确定时将依据GB50009－2012《建筑结构荷载规范》［34］与JGJ 3－2010《高层混凝土结构技术规程》［2］中的荷载效应基本组合进行。则剪力墙抗弯承载力极限状态的荷载效应基本组合表达式为：

式中：γG、γQ、γW分别为永久荷载、楼面活荷载、风荷载的分项系数；ψQ、ψW分别为活荷载和风载的组合值系数；SGk、SQk、SWk分别为永久荷载、楼面活荷载、风荷载的荷载效应标准值。为方便后续计算，作如下处理：

故根据规范中荷载效应基本组合与分项系数、组合值系数取值获得的荷载效应基本组合表达式见表8所示。

表8 荷载效应基本组合表达式Table 8 Expressions for basic combinations of load effects

3.6 可靠指标计算说明

在确定荷载效应和抗力的统计参数后，可建立剪力墙抗弯承载力的功能函数表达式为：

式中：SG、SQ、SW分别对应永久荷载、楼面活荷载、风荷载的荷载效应（等于荷载效应标准值与分项系数的乘积）。因此，其相应的剪力墙抗弯承载力极限状态方程为：

在确定上述各项之后，可进行式（1）～式（4）在进行装配式剪力墙的抗弯承载力计算时可靠指标计算。在计算时，将墙体截面受压区端部钢筋合力点与受压区外边缘之间的距离a′s、实际轴压比n视为确定型变量，其他参数均视为随机变量。将楼面活荷载按住宅和办公楼分开计算，同时根据规范［2－3］构造要求并结合文献［33］的考量，混凝土强度等级取C30～C60，剪力墙钢筋等级取HRB400（目前高层建筑中剪力墙钢筋已基本采用HRB400级钢筋），腹板纵向钢筋配筋率ρw取0.25%～0.40%，边缘构件纵向钢筋配筋率ρs取0.6%～2%，实际轴压比n取0.05～0.30，ρ取0.1～2.0，w取0～40。下述计算如无特别说明，混凝土强度等级选取C30，ρw=0.25%，ρs=0.8%，n=0.1，ρ=0.5，w=10。

式（1）～式（4）在进行装配式剪力墙的抗弯承载力计算时可靠指标计算步骤如下：

（1）假定永久荷载标准值SGk值，根据式（12）～式（13）计算出SQk、SWk；

（2）根据式（15）计算抗力R值；

（3）将式（9）～式（10）代入几何参数不确定性统计参数、材料参数不确定性统计参数、计算模式不确定性统计参数计算R的统计参数；

（4）根据所求得的SGk、SQk、SWk、R及对应的统计参数求解各变量的均值、标准差；

（5）利用式（14）作功能函数，采用JC法求解可靠度指标。

3.7 可靠指标计算结果分析

按照3.6节中步骤和方法，计算不同轴向压力、混凝土强度、腹板纵向钢筋配筋率、边缘构件纵向钢筋配筋率下装配式剪力墙采用规范［2－3］中剪力墙的抗弯承载力公式进行设计的可靠度指标，并与目标可靠度指标［β］进行对比分析。根据规范［4］选取安全等级为二级、破坏类型为脆性破坏对应的目标可靠指标［β］=3.7作为标准来评估式（1）～式（4）在进行装配式剪力墙的抗弯承载力设计时的可靠性。

（1）楼面活荷载与永久荷载效应比ρ的影响

表9总结了住宅、办公楼面活荷载与永久荷载效应比ρ对应的可靠指标β计算结果。从表9可以看出，随着ρ值的增加，住宅和办公楼面活荷载的可靠指标均呈现增大趋势，且住宅、办公楼面活荷载的可靠指标随着ρ从0.1增加到2.0过程中分别增加了5.33%、6.62%。而同等ρ值下，办公楼面活荷载的可靠指标基本都略大于住宅楼面活荷载的可靠指标。此外，同样可以发现，住宅和办公楼面活荷载的可靠指标均未达到目标可靠指标3.7的要求。

表9 ρ对可靠指标的影响Table 9 The effect of ρ on reliability index

（2）风荷载与永久荷载效应比ω的影响

表10总结了住宅、办公楼面活荷载下不同风荷载与永久荷载效应比ω对应的可靠指标β计算结果。从表10数据可知，随着ω值的增加，住宅、办公楼面活荷载的可靠指标基本呈现减小趋势，且住宅、办公楼面活荷载的可靠指标随着ω从0增加到40过程中分别减小了20.07%、23.71%。同样可以发现，同等ω值下，办公楼面活荷载的可靠指标基本也都略大于住宅楼面活荷载的可靠指标。此外，除了ω为0、0.25、1时的住宅楼面活荷载及ω为0～1时的可靠指标大于目标可靠指标外，其余均小于目标可靠指标，最终的可靠指标均值也小于目标可靠指标。

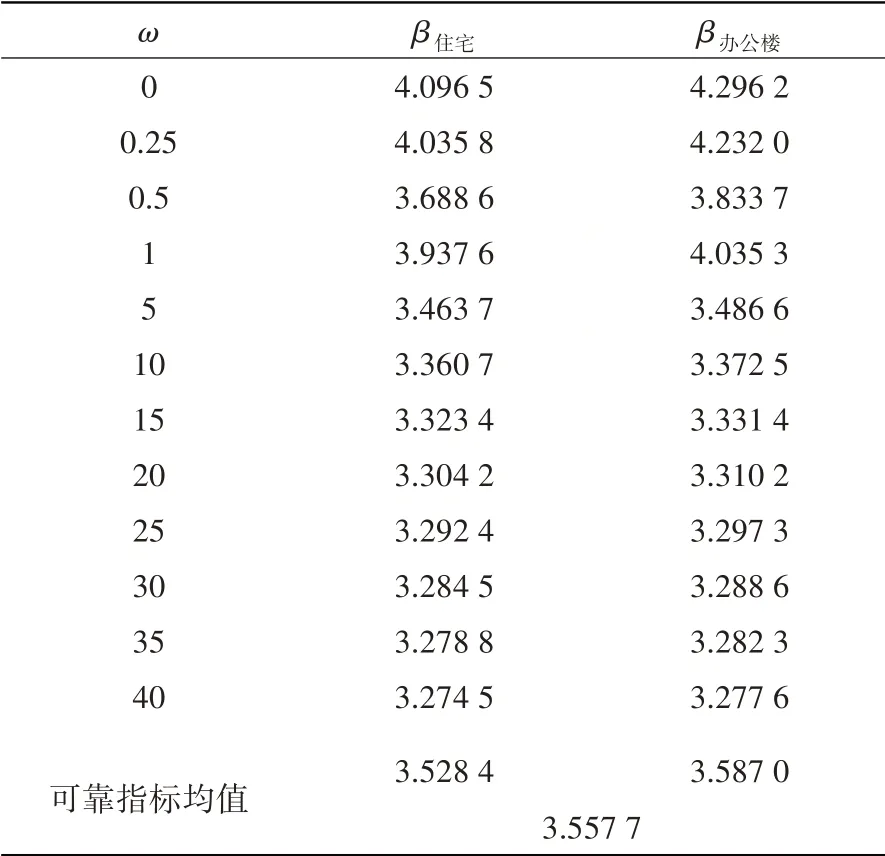
表10 ω对可靠指标的影响Table 10 The effect of ω on reliability index

（3）混凝土强度、实际轴压比n的影响

分别计算住宅、办公楼面活荷载下不同混凝土强度、实际轴压比n对应的可靠指标β见表11所示。从数据可以看出，不同混凝土强度等级对可靠指标影响非常小，且不同混凝土混凝土强度等级下的可靠指标均未达到目标可靠指标要求。这也同样说明，混凝土强度等级并非剪力墙抗弯承载力可靠指标的主要控制因素。从不同实际轴压比n对可靠指标的影响分析可知，可靠指标随着n值不断增大而增大。这主要是因为随着剪力墙实际轴压比（在一定范围内）增加，剪力墙的抗弯承载力不断增大，即剪力墙抗力不断增大，而可靠指标计算的功能函数中荷载效应值一直保持不变，因此导致可靠指标随着实际轴压比n的增加而不断增加。这也同样说明一定范围内的轴压比能够增强剪力墙的抗侧向能力的可靠指标。最终，住宅、办公楼面活荷载在不同混凝土强度、实际轴压比n下的可靠指标均未达到目标可靠指标3.7的要求。

表11 混凝土强度、实际轴压比n对可靠指标的影响Table 11 The effect of concrete strength，actual axial load ratio n on reliability index

（4）纵向钢筋配筋率ρs、ρw的影响

分别计算住宅、办公楼面活荷载下不同纵向钢筋配筋率ρs、ρw对应的可靠指标β见表12所示。由表12数据分析可知，随着纵向钢筋配筋率ρs、ρw增大，住宅、办公楼面活荷载的可靠指标不断降低。这是因为随着纵向钢筋配筋率ρs、ρw的增大，虽然抗力统计参数中的均值和变异系数均略有减小，但变异系数减小对可靠指标的影响没有均值减小对可靠指标的影响大，这导致最终可靠指标出现减小趋势。总体而言，纵向钢筋配筋率对可靠指标影响幅度较小，而且住宅、办公楼面活荷载在不同纵向钢筋配筋率ρs、ρw下的可靠指标均未达到目标可靠指标3.7的要求。

表12 纵向钢筋配筋率ρs、ρw对可靠指标的影响Table 12 The effect of longitudinal reinforcement ratio ρs，ρw on reliability index

4 基于可靠指标的装配式剪力墙抗弯承载力设计公式修正

根据上文分析结果表明，采用规范中现浇剪力墙抗弯承载力设计公式进行“等同现浇”的装配式剪力墙抗弯承载力设计的可靠指标在多数情况下难以达到目标可靠指标的要求。为达到目标可靠指标要求，需要将规范中现浇剪力墙抗弯承载力设计公式进行修正后用于装配式剪力墙的抗弯承载力设计。文中参照钢筋混凝土轴心受压构件的承载力计算公式的表达形式，通过引入可靠度指标调整系数方式以达到上述要求。修正后的抗弯承载力FR计算公式如下：

式中：φ为可靠指标调整系数；F为按式（8）计算获得的抗弯承载力。

由上文分析结果可知，混凝土强度、纵向钢筋配筋率ρs与ρw对可靠指标的影响幅度都不超过5%，而一定范围内的实际轴压比n对可靠指标有利，楼面活荷载与永久荷载效应比ρ对可靠指标有一定影响，风荷载与永久荷载效应比w对可靠指标影响最大。因此，在对修正式（16）进行可靠指标分析时，主要考虑在n=0.05情况下不同ρ、w对可靠指标的影响，ρ取值0.1～2.0、w取值0～40，其他各项变量取值均参照第3.6节所述。式（16）中可靠指标调整系数φ值等于公式修正前计算模式不定性变量的均值与通过JC法反算在给定可靠指标目标值下的式（16）中计算模式不定性变量的均值之比。

通过JC法反算并在给定可靠指标目标值［β］=3.7下，式（16）中计算模式不定性变量的均值为1.093，故φ的平均值为0.97。取可靠指标调整系数φ=0.95，则修正后用于等同现浇连接的装配式钢筋混凝土剪力墙的抗弯承载力设计公式为：

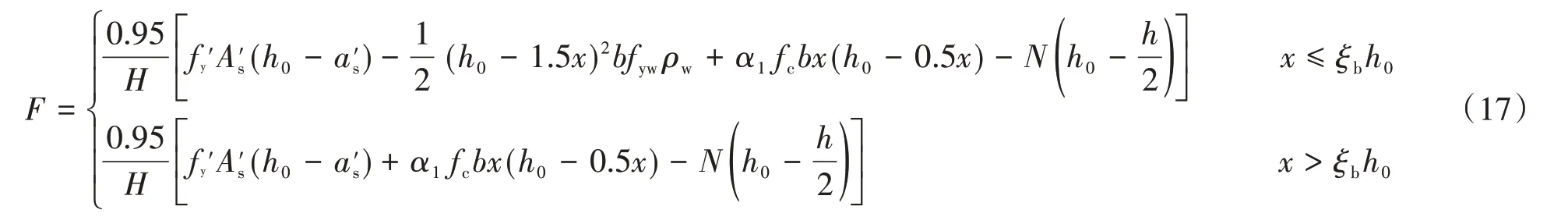
式中：x值按照式（2）确定。

采用式（17）对n=0.05情况下不同ρ、w的可靠指标计算，计算结果见表13所示。根据表13并联合表9、表10对比结果可知，进行公式修正后可靠度指标得到了明显的增加。根据表13及图1的数据分析可知，随着ρ的增加，除w为0、0.25时可靠指标在ρ≤1.0范围内基本呈现递减趋势，在其他情况下可靠指标基本呈现递增趋势；随着w的增加，可靠指标在w≥1范围内基本呈现下降趋势。此外，可以认为在风荷载与永久荷载效应比w≥15后，可靠指标基本不受楼面活荷载与永久荷载效应比ρ的影响。值得说明的是，在w=1附近，可靠指标存在明显的拐点，这是由于荷载效应组合形势发生明显变化导致的。从表13数据分析结果表明，采用修正公式进行装配式剪力墙抗弯承载力计算的可靠指标均值为3.782 8，满足目标可靠指标［β］=3.7要求。

图1 风荷载与永久荷载效应比w对可靠指标的影响Fig.1 The effect of wind load and permanent load effect ratio w on reliability index

表13 n=0.05情况下不同ρ、w的可靠指标计算Table 13 Calculation of reliability index for different ρ，w under the case of n=0.05

5 结论

为了评估采用规范中现浇剪力墙抗弯承载力设计公式进行“等同现浇”的装配式剪力墙抗弯承载力设计的可靠性，文中通过收集国内96片“等同现浇”的装配式钢筋混凝土矩形截面剪力墙试验数据，对其可靠性进行可靠度分析，经过分析论证得出以下结论：

（1）采用规范中现浇剪力墙抗弯承载力设计公式进行“等同现浇”的装配式剪力墙抗弯承载力设计的准确性能够得到很好地保证，而且公式对剪跨比≥2的墙体墙体计算结果比剪跨比＜2的墙体计算结果更加准确。另外，该公式对采用套筒连接的墙体连接的装配式剪力墙计算结果更加贴近试验值，说明套筒连接的墙体连接性能更加贴近现浇墙体；该公式由于并未考虑双倍搭接钢筋面积对抗弯承载力的影响，因此对采用搭接连接的墙体连接的装配式剪力墙计算结果偏小。

（2）采用规范中现浇钢筋混凝土剪力墙抗弯承载力公式进行可靠度分析的结果表明，等同现浇连接的装配式钢筋混凝土剪力墙采用规范中现浇钢筋混凝土剪力墙的抗弯承载力公式进行抗弯承载力计算的可靠指标不满足目标可靠指标［β］=3.7的要求。且分析结果表明，混凝土强度、纵向钢筋配筋率ρs与ρw对可靠指标的影响幅度均不大，而一定范围内的实际轴压比n对可靠指标有利，楼面活荷载与永久荷载效应比ρ对可靠指标有一定影响，风荷载与永久荷载效应比w对可靠指标影响最大。

（3）通过对规范中现浇钢筋混凝土剪力墙抗弯承载力设计公式乘以0.95的可靠指标调整系数，获得可用于等同现浇连接的装配式钢筋混凝土剪力墙抗弯承载力设计的修正公式，并对其进行可靠性检验，检验结果表明修正公式计算结果满足目标可靠指标［β］=3.7的要求。文中所提修正公式可为规范修订提供参考。

（4）文中在进行“等同现浇”的装配式钢筋混凝土剪力墙抗弯承载力公式可靠性分析时，荷载效应组合并未考虑地震作用，关于该公式的抗震可靠度分析仍有待进一步研究。