基于Matlab的模拟滤波器仿真设计

关云静

(西安交通工程学院 中兴通信学院，陕西 西安 710300)

0 引言

模拟滤波技术在信号处理中的作用是十分重要的，因此对模拟滤波器的仿真设计有很大的研究空间和研究价值。

本文首先研究了模拟滤波器的工作原理，然后采用Matlab软件[1]，对低通滤波器进行仿真设计，根据频率变换的方法设计出其他类型的滤波器[2]。

1 滤波器

1.1 滤波器的类型

滤波器可以按照通过的频率范围进行分类，可以细化分为低通、高通、带通和带阻等。低通的含义是指能够通过低频分量的同时抑制高频分量；高通和低通的含义是相反的，是指能够通过高频分量抑制低频分量；带通的含义是指能够使设定的频率通过而没有设定的频率被抑制；带阻和带通的含义是相反的，是指能够抑制设定的频率而没有设定的频率被允许通过。滤波器的分类如图1所示。随着科学技术的发展，在以上基础上新型的滤波器正被不断研发。

1.2 模拟滤波器的特点

模拟滤波器是指处理模拟信号，数字滤波器是指处理数字信号。模拟滤波器是指处理模拟信号，数字滤波器是指处理数字信号。模拟滤波器和数字滤波器的系统函数的表示方式不同，模拟滤波器的系统函数用H(s)表示，数字滤波器的系统函数用H(z)表示。模拟滤波以幅频特性的逼近为主要原则。数字滤波器主要是为了实现相位的匹配。不同滤波器的特点是不同的，比如说巴特沃斯滤波器带阻特性比较平坦，截止特性和相位特性都比较好，对构成滤波器的器件要求比较低，在实际中能够很容易达到设计值的要求。切比雪夫滤波器优点是截止特性较好，缺点是相位特性和群时延特性一般不能满足要求。贝塞尔滤波器的通带内延时特性比较平坦，能够在实际中无失真地传输频谱较宽的信号，但对于贝塞尔滤波器来说，它的截止特性一般不满足要求。从上述分析中可以看出，对于不同的滤波器来说，不同的滤波器特点是不同的，要设计模拟滤波器，首先就需要确定低通原型滤波器，其他类型的滤波器可以在低通原型滤波器的基础上通过频率变换得到。

图1 滤波器的种类

2 模拟滤波器设计原理

2.1 低通原型滤波器设计原理

要设计模拟滤波器，需要根据技术指标确定滤波器的传递函数H(s)[3]。确定H(s)过程中，必须找到合适的逼近函数。目前，应用得比较多的是采用巴特沃斯滤波器设计低通滤波器[4]。

式中：N是滤波器的阶数，ωc是3 dB的截止频率，ωc在ω=ωc附近，随着ω增加，幅度则会下降。

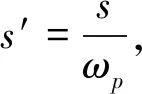
查表得到N=7的巴特沃斯多项式如下：

2.2 频率变换

频率变换是一种滤波器的设计方法，它将一个频段变换为另一个相应的频段[5]。通过频率变换可以在低通滤波器的基础上设计其他类型的滤波器。首先确定出低通原型滤波器的传递函数H(s)，然后根据低通滤波器的设计方法设计了低通原型滤波器，最后通过频率变换设计出其他类型的滤波器。

频率变换步骤如图2所示。

图2 模拟滤波器设计原理

由此可知，要想通过频率变换设计出不同种类的滤波器需要按要求设计出低通原型滤波器，确定其传递函数H(s)，当传递函数已确定便可以通过公式计算出其他类型滤波器的传递函数，进而通过频率变换设计出不同种类的滤波器，而在实际应用中，人们需要电路中的元件进行更改。

3 基于Matlab的模拟滤波器仿真设计

3.1 低通滤波器仿真设计

巴特沃斯低通滤波器幅频特性仿真结果如图3所示。

图3 巴特沃斯低通滤波器幅频特性

由图3可知，随着频率的升高，图像呈现一个下降的趋势，即滤掉了高频信号，保留了低频信号。其图像较为平坦，有较好的滤波功能，符合低通滤波设计要求。

3.2 高通滤波器仿真设计

如果要实现低通到高通的变换，则其对应的频率特性是呈现倒数的关系，则有：

以此便得到了所要求的设计的高通滤波器系统函数H(s′)。

巴特沃斯高通滤波器幅频特性仿真结果如图4所示。

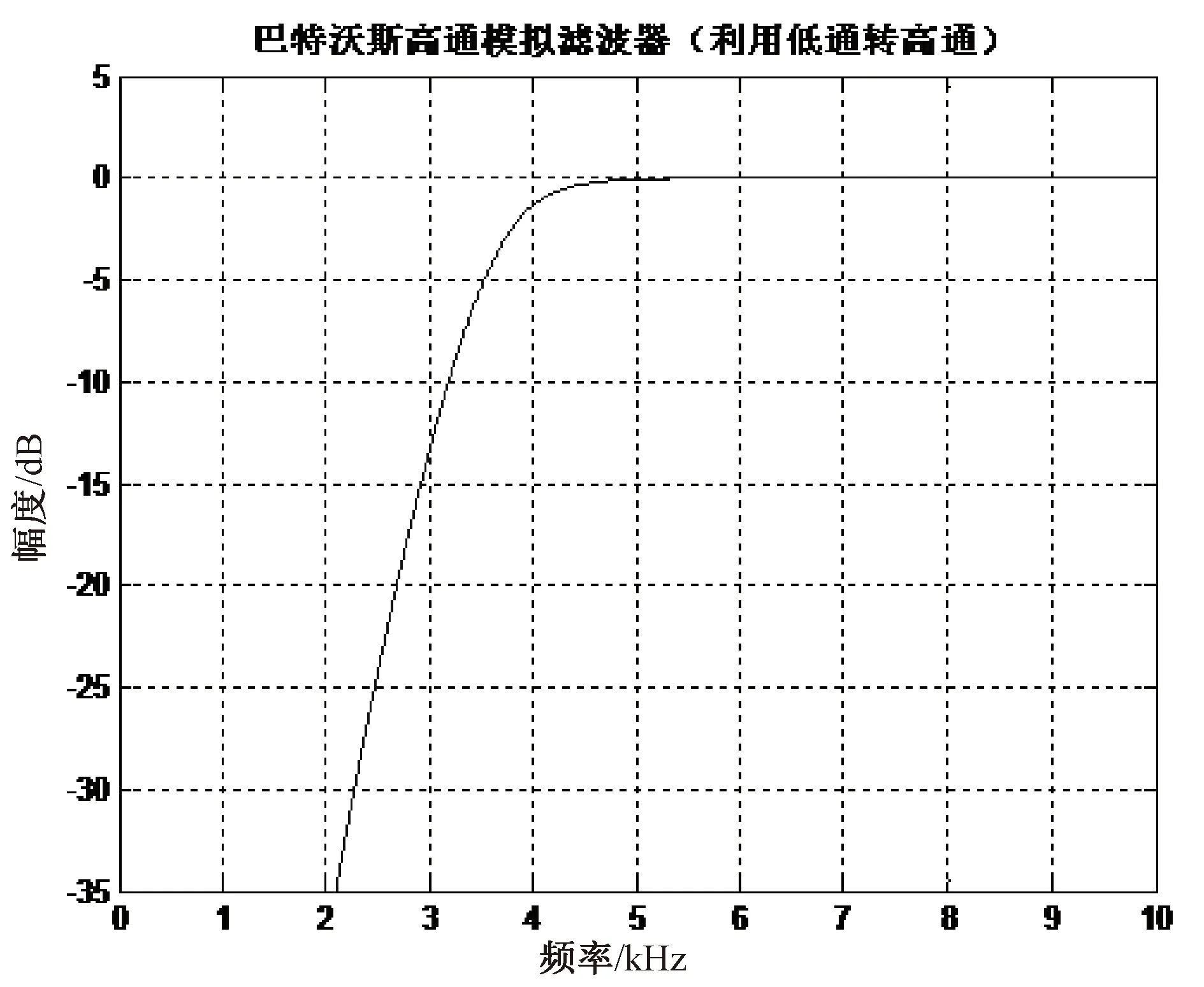
图4 巴特沃斯型高通滤波器幅频特性

由图4可以看出，随着频率的升高，图像呈现一个上升的趋势，与低通滤波器相反，高通滤波器是为了滤掉信号中低频信号，保留高频信号，图像曲线较为平坦，过滤的信号不易产生失真，所以符合高通滤波要求。

3.3 带通滤波器仿真设计

与低通到高通的变化不同，带通滤波器需确定二元参数，先把低通滤波器频率取归一化，参考频率一般取带通滤波器的频带宽度，ωr=ωp1-ωp2，归一化后的带通滤波器系统函数为Hα(jφ)。此映射关系的ω′和ω满足以下公式。

并由此式可以求出带通滤波器的中心频率ω0。

综上，便可通过低通原型滤波器设计出要求的带通滤波器。

巴特沃斯带通滤波器幅频特性仿真结果如图5所示。

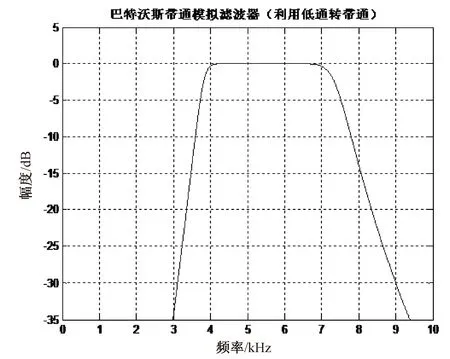
图5 巴特沃斯型带通滤波器幅频特性

带通滤波器的含义是符合的频率分量可以允许通过，不符合的频率分量被屏蔽。由带通滤波器幅频特性图5得知，图像中间平缓，两边呈衰减趋势，过滤出所需要的指定频段的波形，且不易产生失真。

3.4 带阻滤波器仿真设计

带阻滤波器是为了抑制某一频率信号而对其他频率信号不抑制，而其转变过程与低通到带通相似，其归一化后复频率s与带通归一化后的复频率成倒数关系，也可以通过Matlab对其进行实现。

巴特沃斯带阻滤波器幅频特性仿真结果如图6所示。

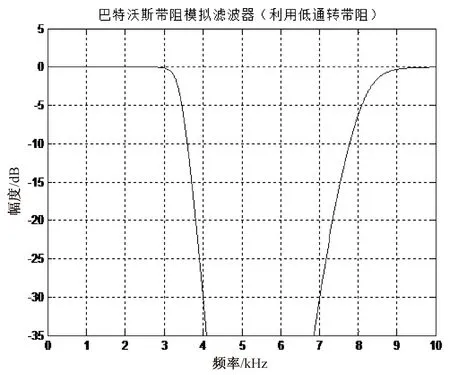
图6 巴特沃斯型带阻滤波器幅频特性

通过定义可以看出，带阻滤波器与带通滤波器的功能正好相反，带阻滤波器能够抑制某些频率的分量，通过某些频率的分量。由图6可以看出，图像从中间凹下并向两边呈上升的趋势，将一定频率的分量进行阻隔，一定的频率分量通过的特性，符合带阻滤波设计要求。

4 结语

经过上述分析，首先确定了低通原型滤波器的传递函数H(s)，由此实现了低通滤波器的设计。对于其他滤波器通过频率变换即可得到，进而采用Matlab软件绘制滤波器的幅频特性曲线，并由图形得知经过频率变换得出几种滤波器符合设计的要求，因而达到了设计目的。