基于课程思政理念下概率论与数理统计教学改革与实践探索

徐旭华，赵春燕，李玲，王妍，钟琴，陈相兵，李亮

（1.四川大学锦江学院数学学院，四川 成都 610207；2.安徽理工大学 力学与光电物理学院，安徽 淮南 232001）

为深入贯彻落实习近平总书记关于教育的重要论述和全国教育大会精神，教育部印发关于《高等学校课程思政建设指导纲要》的通知，要求各高校根据具体课程、具体情况制定好切实有效的教学改革计划，把专业知识与育人目标统一起来。概率论与数理统计课程蕴藏了丰富的哲学思想及数学文化，可以与马克思主义的基本观点有效结合起来，通过合理的教学案例，使学生的科学精神、思辨思维与伦理意识得到培养，增强他们立志报国、为民服务的责任感。概率论与数理统计课程思政教学改革的目的是希望利用教学实践的阵地，将大思政教育理念布局到教学的全过程，将知识传授、能力培养和思想引领有机统一起来。张艳等从教学实践的角度出发，提出了课程思政的案例专题研究原则［1］；黄昱等从时代意义上说明了课程思政的重大意义及其规范性［2］；吴红艳等从方法途径方面延伸了课程思政的内涵［3］；彭丹等从现实背景中找触点［4］，将典型思政案例整合到教材知识点中。对于思政资源的挖掘，目前的研究仅停留在某一章节的某一知识点上，缺乏系统性的提炼、梳理、研究与创新。文章尝试在宏观层面，基于知识间的逻辑性、相合性与统一性，对概率论与数理统计教学中所涉及的思政资源进行整合与分类，进一步扩大育人面的广度和深度。

1 概率论与数理统计中蕴藏的思政内涵

概率论与数理统计课程共有26个主要知识点，其中，和思政元素或数学文化有关联的有12个，大约占比46%.只注重知识传播的传统教学方式无法适应新时期的学生成长需求，迫切需要将冷冰冰的知识转化成有温度的价值能力，这就要求教育工作者深挖课程中的思政资源。

1.1 弘扬爱国精神，传承优秀传统文化

在讲解第一章序言部分时，可以介绍数学家许宝騄举世公认的学术成就，他勉励学生潜心钻研知识，以严谨务实的态度树立伟大理想，为实现中国梦［5］添砖加瓦。在中国长达五千年的文化进程中，很早就孕育了概率论与数理统计的思想，它们以诗歌、谚语等形式流传至今，如唐代·佚名《菩萨蛮·敦煌曲子词》中“枕前发尽千般愿，要休且待青山烂。水面上秤锤浮，直待黄河彻底枯。白日参辰现，北斗回南面。休即未能休，且待三更见日头”。这首古诗描绘了随机事件、必然事件、不可能事件等。“常在河边走，哪有不湿鞋”则是小概率事件的原理。在知识引入的过程中，可以使用诸如这样的中华符号让学生了解数学知识在实际生活中的应用，潜移默化地引导学生加强对自身文化血脉的认同和自信。

1.2 践行社会主义核心价值观——法治

《法句经》里记载“莫轻小恶，以为无殃，水滴虽微，渐盈大器，凡罪充满，从小积成”。在概率论与数理统计这门课程是小概率事件应用的范例。例如，一个小偷偷东西，假设每次盗窃的行为是独立的，如果每次他行窃时被抓住的概率为0.05，那么随着偷窃行为次数的增加，小偷至少被抓住一次的概率是多少？

设事件A表示小偷至少被抓住一次，Ak(k=1,2,...,n)表示小偷第k次偷窃被抓住，则

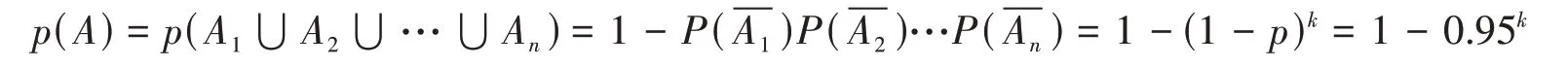
表1 偷窃次数的分布律

由表1可以看到，第75次时，小偷被抓住的可能性已经很大了。通过这个案例教育学生在校时要遵守校规校纪，走上社会更要遵纪守法，惩恶扬善，最终通过小概率事件原理将法治理念悄无声息地引入到学生的意识形态中。对于教师而言，要自觉践行教师法，以教师十项行为准则为行动指南，懂得“法”与“治”的道理。作为一般公民要积小法，成大法，为社会主义和谐社会贡献自己的力量。

1.3 坚持社会主义道路，坚定制度自信

以新冠肺炎疫情为例，一些国家选择了寄希望于全民免疫的“躺平”政策，致使国家的病毒感染人数急剧上升，严重地危害了人民的健康，人们连最基本的生存权无法得到保证。而中国政府根据不同阶段的情况，选择不同的管控方式，始终把人民的生活福祉放在首位，那么该采取什么样的核酸检测策略呢？这其实是期望和假设检验在实际生活的应用［6］。假设某地区共有5000人参加核酸检测，已知每人检测呈阳性的概率是0.001，现有单独检验和分组检验两种策略，哪种策略最优？

策略一：采用逐一化验，则检验次数为5000次；

策略二：采用10人为一组的分组检验，如果检验呈阴性则一次通过，如果呈阳性，再逐一检验。设随机变量Xi(i=1,2…,500)为第i组检验所需的检验次数，那么Xi的可能取值要么为1（全阴性），要么为11（阳性逐一化验），其概率值分别为Xi=1意味着第i组10人全阴性，一个人呈阴性的概率为0.999，10个人呈阴性的概率为0.99910，Xi=11意味着第i组至少有1人阳性，也就是全为阴性的逆事件，则其概率为1-0.99910，那么每组需要的平均检验次数为

设策略二总检验次数为Z，则Z=X1+X2+…+X500，有

因此，策略二比策略一更高效。

通过核酸检测案例，引导学生从亲身经历的新冠肺炎疫情出发，理性看待新冠肺炎疫情以及各项防疫措施，让学生认识到中国智慧和中国速度，增强制度认同感，把个人的成长融入伟大民族复兴的进程中，以一种只争朝夕的精神状态去迎接生活的馈赠。

1.4 从量变到质变，培养批判性的科学精神

黑格尔在《逻辑学》的“存在论”中，阐述了质量互变思想，中心极限定理反映了从量变到质变的思想。棣莫弗—拉普拉斯中心极限定理指出，当随机变量越来越多时，二项分布变成了正态分布，独立同分布中心极限定理说明如果随机变量是由许多随机变量的和组成，构成这些随机变量的因素都是微小的、没有一个因素起到决定性的作用，则这个数量指标近似地服从正态分布［7］，由此可以引导学生认识事物变化都是由量变到质变的。以评估体育锻炼为例，设Xi(i=1,2,…,365)表示第i天进行了锻炼，Xi为独立同分布的随机变量序列，E(Xi)表示第i天锻炼的综合效果，表现如体质增强等，D(Xi)表示为第i天锻炼后的感受差异程度，表现如过度疲劳等，假设E(Xi)=65.6,D(Xi)=28.282，X表示一年的体育锻炼效果，则

上述结论表明，坚持锻炼的效果很明显，体现在均值较大，而方差较大，说明需要改进锻炼的方式技巧。教育学生不要轻视小问题，不要蔑视小成就，要重视日常积累，养成良好的生活学习习惯。

在概率论与数理统计的发展进程中，从古典概率到几何概率，统计概率再到概率的公理化定义，提供了理解概率收敛的理论基础。在概率论的公理化体系建立以后，大数定律可在理论上进行严格的证明而成为意义明确的定理，尤其在1733年到1937年间，从De Moivre首次得出了一个特殊版本的中心极限定理到Feller和Levy给出中心极限定理的充要条件，例如：

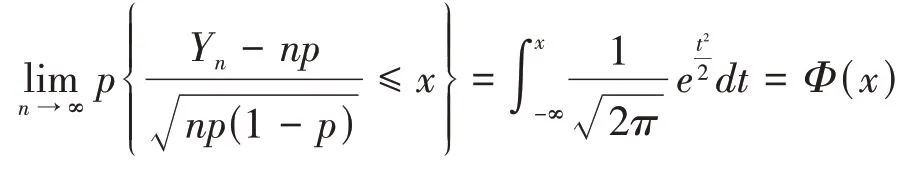
该定理是概率论与数理统计历史上第一个中心极限定理，由棣莫弗于1730年给出的特殊情况，几十年后经拉普拉斯推广到0＜p＜1的一般情形。无数伟大的数学家、统计学家经过一场跨越两百年的探索，概率论与数理统计才发展成一门独立学科。这场伟大实践处处体现了对立统一规律、量变质变规律、否定之否定规律，彰显了科学精神的精髓实质，让学生感受到数学独特的严谨之美，培养他们缜密、批判、务实的逻辑思维。

1.5 感知唯物主义辩证法，从偶然性到必然性

随机现象的规律性只有在相同的条件下进行大量重复试验时才会呈现出来。如在实践中人们认识到大量测量值的算术平均值具有稳定性，大数定律表达并证明了这种规律性［8］，即随机现象的平均结果不再受个别事件的影响，而是呈现出某种规律性。例如，抛掷硬币，设n表示实验次数，nH表示正面出现的次数，f表示频率，当抛掷次数较少的时候，正反两面出现的次数会有明显的差异，这是偶然性，但当抛掷次数很多的时候，正反两面出现的次数就“几乎”一样，这是必然性，如表2所示。教育学生坚持必然与偶然的辩证统一，不被暂时的挫折打倒，不被眼前的荣誉迷惑，要坚定信念，勤奋学习，最终会学有所成，成为对社会有贡献的人［9］。

表2 频率的波动性

1.6 培养马克思主义的基本观点，矛盾的普遍性与特殊性，共性和个性统一

利用矛盾分析法讲解随机变量。首先，随机变量一般分为离散型和连续型，它们是对立统一的，“离散和连续的矛盾，正是推动数学发展的矛盾之一。”在相互转化过程中，绽放出了一种思辨之美，让学生更加深刻地了解它们各自存在的条件，培养了同学们严谨的数学思维［10］。其次，随机变量是一个函数，但它与普通的函数具有本质的差别，普通函数是定义在实数轴上的，随机变量是定义在样本空间上的，这其实是同一个问题的两个方面，体现了共性和个性的统一。最后，从随机事件与随机变量的关系来看，它们都是研究随机现象的手段，随机事件是从静态的观点来研究随机现象，而随机变量则是从动态的观点来研究随机现象。在求解连续型随机变量函数的分布时，利用分布函数求导，得到概率密度是普遍性的思路，而当函数处处可导，且严格单调时，利用公式法求概率密度则是特殊性的方法，这是事物特殊性与普遍性的辩证关系。

1.7 提倡合作共赢，培育集体主义价值观

“一个篱笆三个桩，一个好汉三个帮”“三个臭皮匠，顶个诸葛亮”“人心齐、泰山移”等这些谚语所反映的思想在事件的独立性，泊松分布均有体现［11］。例如，维护80台同类型设备，故障率为0.01，有两种维修方案，方案一是4人维护，每人负责20台，方案二是由3人共同维护。哪种方案更加合理？

方案一：以Ai(i=1,2,3,4)表示事件“第i人维护的20台中发生事故不能及时维修”，X表示“第1人维护的20台中同一时刻发生故障的台数”，则

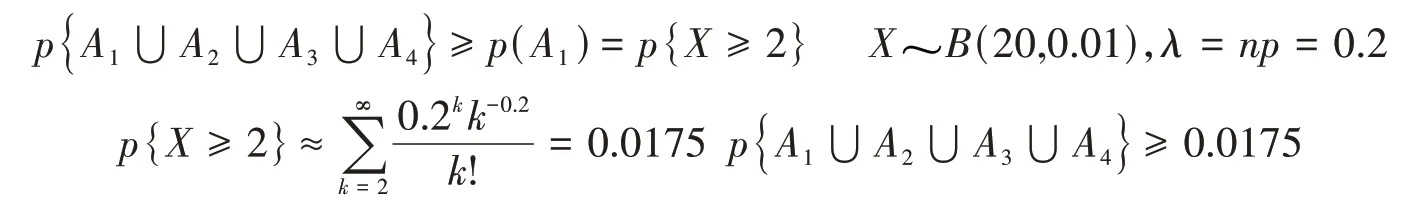
方案二：设Y表示同时发生故障的台数，则有Y～B(80,0.01)，λ=np=0.8，则不能及时维修的概率为

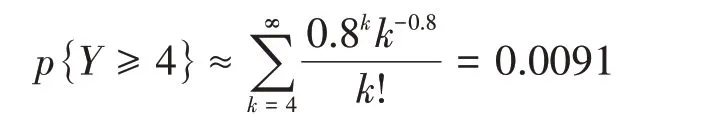
可以看出第二种方案，虽然配备的人员少，但由于团队协作，发生故障后需要等待的概率反而更低。通过此案例引导同学们要培育团队精神，学会依靠集体的力量，让他们体会到团队力量的强大。

1.8 注重隐私，把握敏感性问题的工作方法

全概率公式的基本思想是把一个未知的复杂事件分解成一个个已知的简单事件再求解，这种思想在解决敏感性问题的调查时比较适用，如学生作弊、疾病的感染等。

保密问题：在一个无人的房间里有一个纸箱，假设箱里装有30个球，其中20个红球10个白球；被测试者事先被告知，从这个箱子中随机抽取一个球，看过颜色后放回。

如果学生取的是白球，回答问题A：“你的生日是在10月1日之前吗？”

如果学生取的是红球，回答问题B：“你期末考试作弊了吗？”

学生将结果勾在一张只有“是”与“否”的答卷上，每一位学生都参与了这次测试。回收1200份答卷，如果其中400份答卷回答“是”，那么该校期末考试学生的作弊实际比例是多少呢？对于任意一个被调查者，由于调查者不知道他抽到的是何种颜色的球，所以不会知道他回答的到底是问题A还是问题B，这样就有效保护了被调查者的个人隐私。于是，被调查者可以放心地给出真实答案。

设事件C=“回答“是”，B1=“学生取到了红球”，B2=“学生取到了白球”。由全概率公式，有：

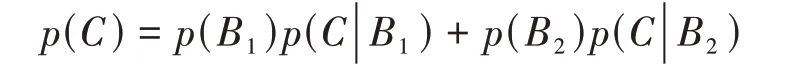
2 优化课程设计，深挖思政资源

重点围绕知识目标、能力目标、育人目标开展教学设计活动，以生活案例［12］或者历史典故为切入点，引发情感共鸣，从而更加有效地挖掘大思政资源，将恰当的“元素点”分享给同学，最终达到将知识传授、能力培养与价值引领有机融合的教学目的。下面以贝叶斯公式为例，详细说明。

（1）引入“烽火戏诸侯”“狼来了”典故，说明了什么哲理？这和这门课程有什么关系呢？

（2）实例教学，“狼来了”寓言中，小孩的诚信度是如何变化的？记A={小孩说谎}，B={小孩可信}，假设p(B)=0.8，根据贝叶斯公式得

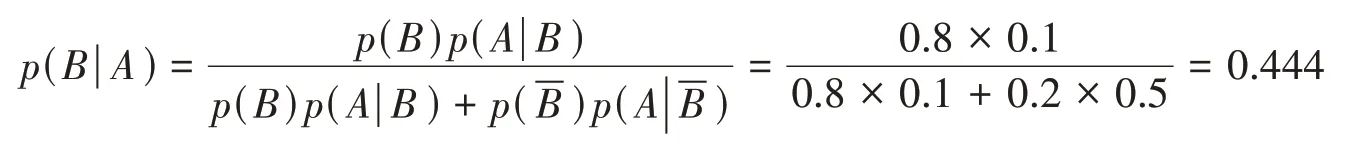
说明村民第一次受骗后，小孩的可信度由原来的0.8下降为0.444，再次使用贝叶斯公式，可计算出小孩第二、三次撒谎后，村民对他的信任度。即：第一次村民对小孩的信任度由0.8下降到0.444.村民第二次听到“狼来了”，发现又被骗后，小孩的信任度由0.444下降到0.138，最后小孩的信任度由0.138下降到0.013（表3）。

表3 可信度变化率

提炼思政元素：社会主义核心价值观“诚信”，“言必行行必果”，村民对小孩的信任度急剧下降，下降的幅度越来越大。

如果小孩认识到错误，他怎么做才能再次取得村民的信任？在此基础上，再用贝叶斯公式来计算，即这个小孩第三次说谎以后，村民对他的可信程度0.013，如果小孩认识到错误并改正：

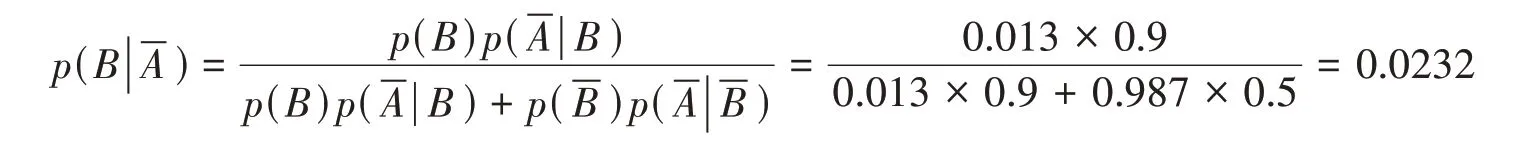
这表明村民经过三次上当，对这个小孩的可信度变为0.013后，小孩第一次诚实，人们对他的可信度变为0.0232.用同样的方法，再用贝叶斯公式来计算，村民对他的可信程度0.0232，如果小孩第二次守信，可信度变化为0.04.用同样的方法得到下面数据：

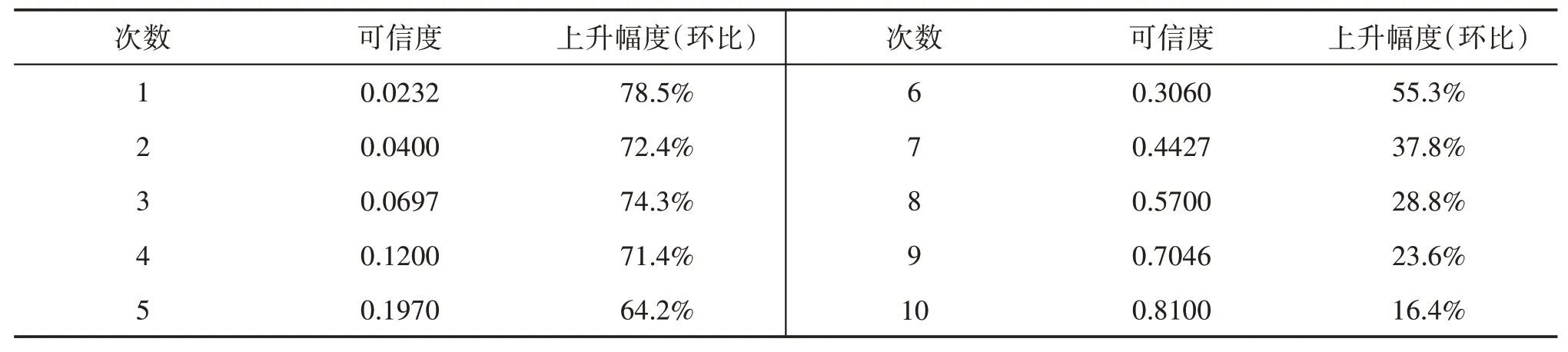
表4 可信度变化率

由表4可知，小孩3次说谎，几乎将诚信度消耗殆尽，但是想要返回到以前，起码需要10次守信。生活中，“第一印象坏了，就很难扭转过来”，培养学生树立正确的价值观，珍惜当下，失去很容易，但是再想恢复到以前就很难了。这就是对社会主义核心价值观“诚信”的教育实践，力争做到知识、情感、价值观的协调共生［13］。

3 教学实践探索

在课程思政教学实践中，以“立德树人”为使命，以“思政育人”为责任，在课程48个学时的教学时间里，将课程中所涉及的思政元素进行了分类处理，并给出了理论课与实践课的建议学时（表5）。

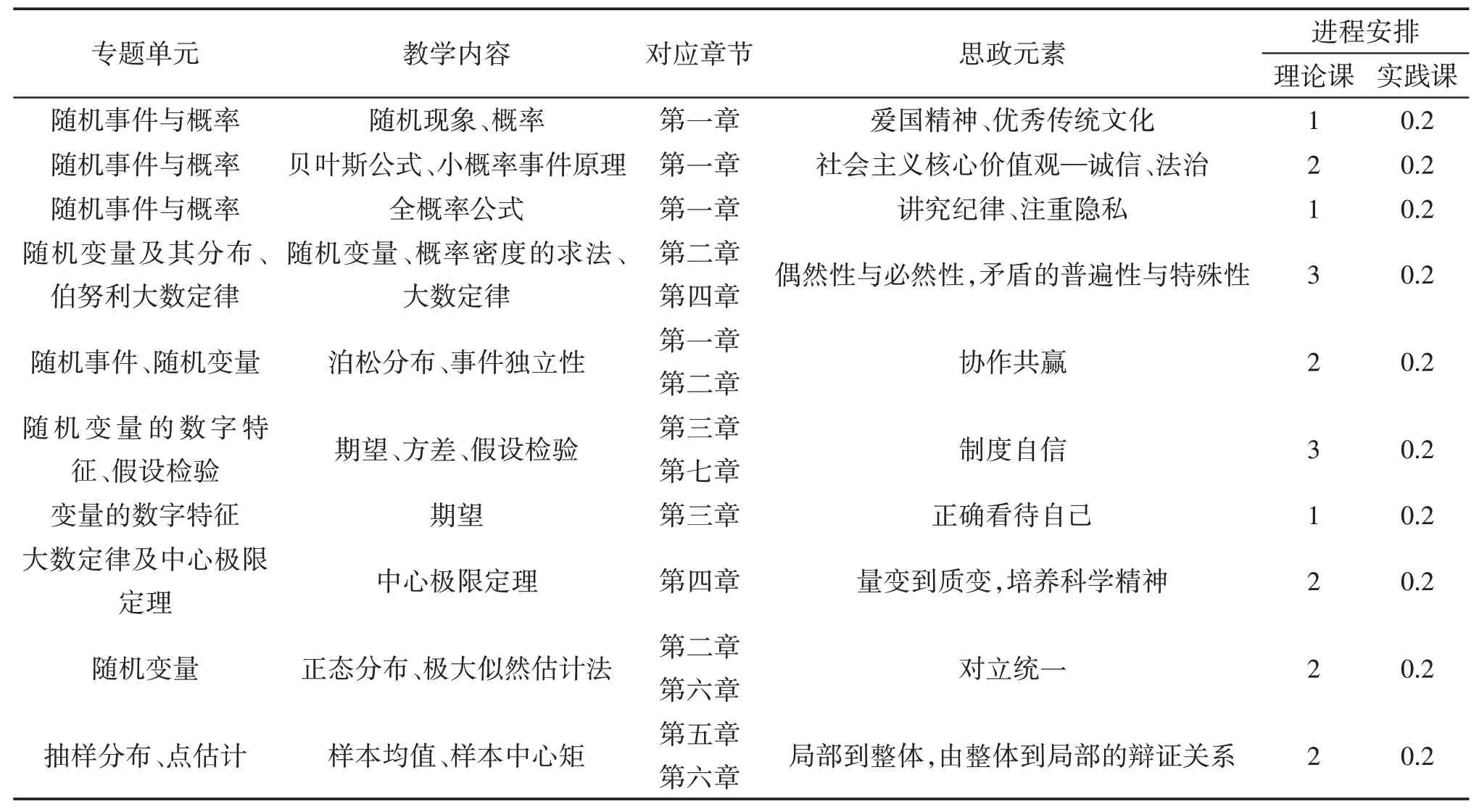
表5 课程思政元素设计与挖掘

利用学校的交互课堂，选择部分班级进行试验，实行混合式教学［14］。立足于课程内容，教学方法，课程思政建设模式等方面，并在以下几个方面进行了改革探索。

（1）使用体现课程思政的新教材。新教材最大的特点是在各个环节加入了思政元素与数学文化，广泛使用案例教学，提高学生学习兴趣和积极性。参加课程思政试验教学探索的班级以新编写的教材作为参考，在教学过程中将思政元素有效提炼出来，达到润物无声的效果，自然生动地触发学生思想奇点。联系一位思政类的教学名师，参与课件与习题册的设计制作，进行教学试点以后，启用体现课程思政理念的新课件。

（2）开展翻转课堂教学，引导学生自己思考，感悟学科中的相关思政理念。概率论与数理统计共有48个学时，选择12个学时进行适度翻转课堂教学实践。教师有针对性地讲解重点、难点、补充知识点，鼓励学生提出问题，以学生讨论为主，教师引导为辅。在这部分教学实践中，课堂借助超星学习通，“雨课堂”平台来辅助课上教学，在课堂中教师会根据教学需要发布抢答、评分等指令，进一步活跃课堂气氛，加强师生互动，鼓励学生主动参与到学习中来，以提高课堂教学效果。

（3）妥善处理好“课前、课中、课后”的关系。课前学生需要进行线上自主预习，带着自己的问题和感悟进行课堂线下学习。课前教师需要给学生推送学习视频［15］，在视频的选择上不是为了传导知识，而是以提高学生兴趣为主，如利用贝叶斯公式寻找马航MH370，课后要布置适当作业，可以尝试布置一些无标准答案的题型，提倡同学们从不同角度思考解决。