道岔转辙机自供能传感器设计与能量俘获特性试验

李守太， 高鸣源， 杨明金， 王平， 张丽， 陈子文， 李云伍， 蒲应俊

1. 西南大学 工程技术学院/丘陵山区农业装备重庆市重点实验室,重庆 400715； 2. 西南交通大学 土木工程学院/高速铁路线路工程教育部重点实验室,成都 610031； 3. 西南大学 出版社,重庆 400715

轨道交通作为重要的客运、物流载体,近些年在全世界范围内得到了大力发展.以中国为例,截至2020年底,营业里程超过14万km,当年铁路投产新线超过1 300 km和投资额达8 000亿元[1].轨道交通道岔系统是保障轨道列车按照既定路线安全行驶的“方向盘”,通过道岔系统的核心组成部分道岔转辙机牵引拉杆进行横向推动道岔运动,进而实现轨道列车转向[2-3].道岔转辙机工作质量的好坏,直接影响轨道交通的行车效率,更关系到轨道交通运行安全,对其进行实时监测非常必要[4-5].随着轨道交通里程的增加和服役状态的劣化,道岔转辙机故障率逐渐增高.根据国家铁路局和地铁运营企业近年报告,道岔转辙机故障分别占铁路运输和地铁设备总故障件数的18%和50%～60%[6-7],因此对道岔转辙机牵引拉杆插销进行拉力监测(包括拉力状态是否平稳、拉力是否超限而导致插销变形和断裂)具有重要作用.现有道岔转辙机拉力监测能量供给依靠外置电源,采用定期巡检发现问题再维修的方案[8-9],可能出现拉力异常导致转辙机故障而没有及时发现并排除而危及行车安全.本研究基于振动能量采集技术的轨道道岔转辙机自供能传感器的设计,能够实现道岔转辙机拉力实时监测的能量自供给,可以有效预防脱轨等安全事故,其安装位置如图1所示．

图1 道岔转辙机及自供能传感器安装位置

道岔转辙机故障诊断研究方面,孙孟雷[10]提出了基于道岔信号形状特征的功率信号神经网络故障诊断方法,构建了不同时间尺度下特征图的卷积神经故障诊断模型,故障诊断正确率达99.5%； 陈海欢[11]在道岔转辙机动作电流原始数据类型及深度学习模型适用范围的基础上,建立了道岔转辙机故障诊断模型,通过对模型结构的不断优化,使道岔转辙机故障分类具有更高准确率； 张钉[12]以微机监测系统采集的道岔转辙机动作功率曲线为数据源,提出小波变换和改进BP(Back Propagation,反向传播)神经网络相结合的S700K型转辙机故障诊断模型,也取得了较好效果.上述研究基于对道岔转辙机采集到的信号进行处理和建模来判断道岔转辙机性能状况,而对于道岔转辙机拉杆实时监测传感器和能量自供给等方面研究较少．

道岔转辙机电源通常为380 V交流电源,需要增加额外的电流转换等设备才能被监测设备使用,导致额外的投入和维护成本增加.振动能量收集技术是将列车通过轨道时的振动能量转换为电能,变废为宝的同时提高能源利用效率[13-14],振动能量俘获装置可以允许长时间地支持传感器运行,而无需更换电池或在传统电池无法正常运行的恶劣环境中供能给传感器[15-16].常用的振动能量俘获类型主要有电磁式[17-19]、压电式[20-21]、静电式[22-23],许多研究学者进行了卓有成效的研究.Gao等[24]设计了一款由磁悬浮能量采集器供电的轨道式能量传感器,验证了列车在某时速行驶下传感器峰值电压输出性能,且传感器能够实现与控制端的无线通信.Jung等[25]设计了压电和电磁发电机组成的椭圆形混合式能量采集器,该混合式能量采集器在60 Hz和50 m/s振动下实现25.45 mW的平均功率输出.Zhao等[26]提出了一种新型的接触分离模式的悬臂式摩擦电能量采集器(Triboelectric Energy Harvester,TEH),并对其性能进行了理论研究和实验测试,在5 m/s2的加速度和8 Hz的激励频率下可获得25 V的峰值输出电压.孔令强等[27]设计了一种安装在列车转向架上的双自由度振动俘能器,并通过理论分析和试验检验了不同自由度下俘能器的性能； 高鸣源等[28]提出轨道振动―电磁耦合动力学模型,计算车辆行经轨道结构时磁浮俘能器的动力响应.道岔转辙机多处于户外或偏远地区,采用人工对监测设备的电源进行更换会导致较高的维护成本,研究俘获轨道振动能量为道岔转辙机轴销传感器供电具有很大的现实意义[29-30]．

轨道交通能量俘获装置一般需要额外安装在轨道交通运营系统中,可能会影响列车的正常运营,进行现场试验难度极大.目前轨道交通能量俘获装置性能验证普遍采用的方法仍为仿真模拟、理论分析和室内试验[31-32],而对于室内试验,主要存在以下问题：(1) 多数学者在室内振动台试验输入的振动信号主要是正弦扫频和自编随机信号,未能将采集到的轨道实测路谱信号通过室内振动台复现； (2) 轨道实际路谱特点为小位移幅值和大加速度,加速度控制策略容易超限且不能直观地反映速度与黏性阻尼式电磁发电量的关系.磁体与闭合线圈发生相对运动时,两者之间会由于电磁阻力而阻碍相对运动,这一现象可用楞次定律解释,同时,磁体在运动的过程中还将受到机械阻尼的作用.可动磁体在管内运动过程中受到的阻尼力可简化表述为F=-(cm+ce)v,cm为系统机械阻尼系数,ce为系统的电磁阻尼系数,v为磁体与线圈的相对运动速度[33],因此,可以认为这是一个线性黏性阻尼系统．

本研究设计了一种基于振动能量俘获技术的轨道道岔转辙机自供能传感器系统,主要由轴销传感器、振动俘能装置和数据处理模块组成.本研究的主要贡献为：(1) 轴销传感器本身既是结构紧固件又是传感器； (2) 振动俘能系统利用列车通过时的振动能量,同时结合可充电电池,可以实现轴销传感器全天候能量的持续自供给； (3) 实现了轮轨交互作用(轮轨非线性随机振动)下的轨道振动数据的室内测试．

道岔转辙机自供能传感器工作原理如图2所示．

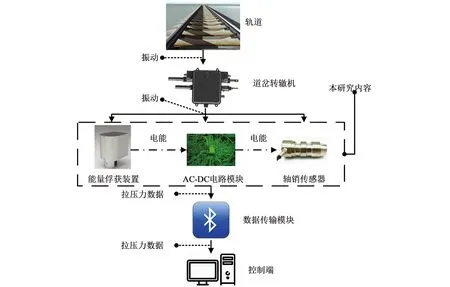
图2 道岔转辙机自供能传感器工作原理

1 自供能传感器机械系统设计

1.1 轴销传感器

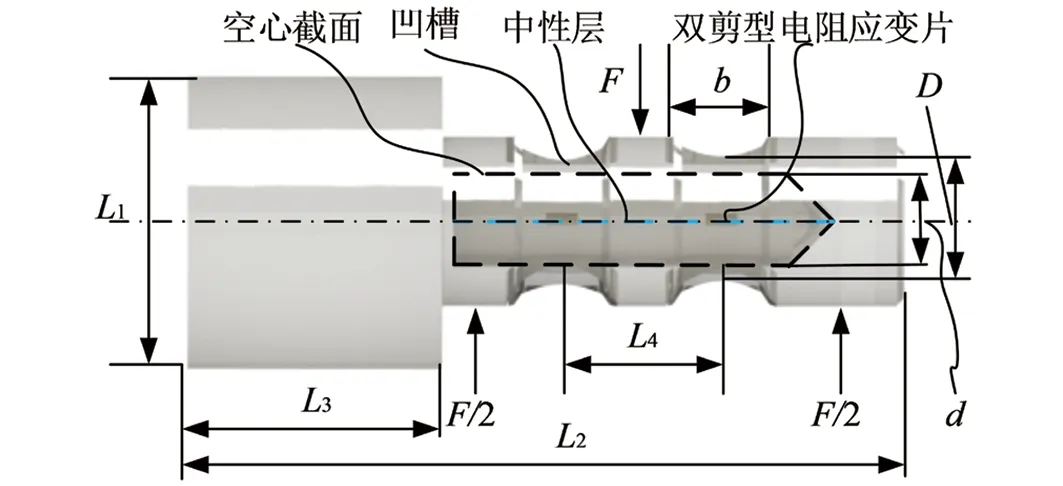
图3 轴销传感器结构

轴销传感器结构简单,是一个没有承载座、力加载头和防护壳的空心截面弹性元件,在工作过程中只承受剪力作用.轴销传感器的表面有对称布置的凹槽,空心截面凹槽的中心位置粘贴有双剪型电阻应变片,布置在两个凹槽处的双剪型电阻应变片共同组成一个惠斯通电桥.具体工作原理为：外力作用改变双剪型电阻应变片几何尺寸的同时改变其电阻,电阻的改变则导致输出电流的改变,进而通过惠斯通电桥产生电压信号,电压信号通过A/D转换为数字信号后被测量,在量程范围内,轴销传感器输出电压的大小与其承受拉力或压力大小成正比[34],轴销传感器结构示意图如图3所示．

空心截面中性层处的最大弯曲应力σmax为

(1)

其中：d为中性层空心截面的宽度,m；D为凹槽最小直径,m．

最大弯曲应变εmax为

(2)

其中：F为轴销传感器承载力,N；E为弹性模量,Pa；b为凹槽的宽度,m．

输出灵敏度S为

S=Kε

(3)

其中：K为双剪型电阻应变计灵敏系数；ε为弯曲应变．

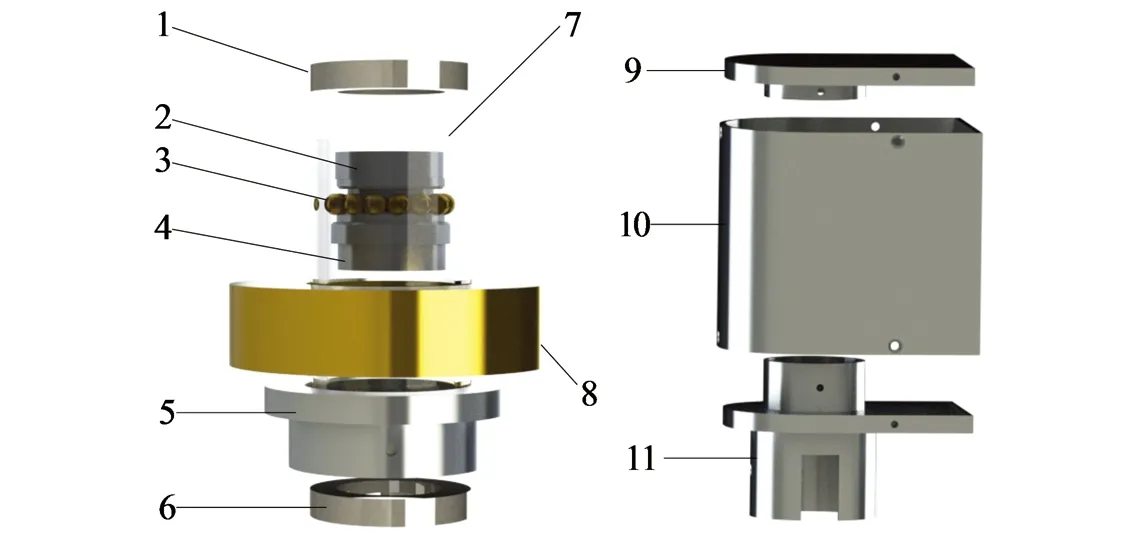
1-上静止磁铁； 2-滑块； 3-铜珠； 4-悬浮磁铁； 5-支撑座； 6-下静止磁铁； 7-有机玻璃管； 8-线圈； 9-上端盖； 10-保护壳； 11-下端盖．图4 振动能量俘获装置结构图

通过分析公式(1)和公式(2)[35]可以得出轴销传感器凹槽的宽度b对整个装置的性能有重要影响,需要保证空心截面中性层处的应力和应变为零件最大值处,一般b值取双剪型电阻应变片基长的2倍.所设计轴销传感器轴销凹槽最小外径D=22 mm,长度L1=38 mm,L2=90 mm,L3=32 mm,L4=20 mm,中性层空心截面的宽度d=10 mm,额定载荷F=10 000 N,材料为40CrNiMoA,弹性模量E=2.1 ×104kg/mm2,输入3～6 V,输出灵敏度为1.5～2 mV/V．

1.2 振动能量俘获装置

本研究振动能量俘获装置类型为电磁式,如图4所示.振动能量俘获装置包括防护壳和磁浮俘能系统,磁浮俘能系统由有机玻璃管、上静止磁铁、下静止磁铁、悬浮磁铁、线圈、铜珠和滑块组成,其中：上静止磁铁和下静止磁铁在上端盖和下端盖的挤压作用下分别固定在有机玻璃管上端和下端,悬浮磁铁固粘于滑块并在有机玻璃管中滑动,上静止磁铁和下静止磁铁之间布置悬浮磁铁并调整磁极的方向以排斥悬浮磁铁,从而形成非线性磁力,通过铜珠使滑块与有机玻璃管之间实现滚动接触来降低二者之间的摩擦阻力.防护壳由上端盖、下端盖和保护壳组成,三者通过螺栓连接形成一个封闭的空间,保护布置在其内部的磁浮俘能系统不受外界环境(如沙尘和雨水等)的影响．

振动能量俘获装置的能量俘获本质是基于法拉第电磁感应定律,悬浮磁铁在上静止磁铁和下静止磁铁作用下处于平衡状态,外界振动打破平衡并使悬浮磁铁在非线性回复力的作用下沿着圆柱形有机玻璃管上下滑动,进而切割磁感线产生感应电压,原理如图5(a)所示．

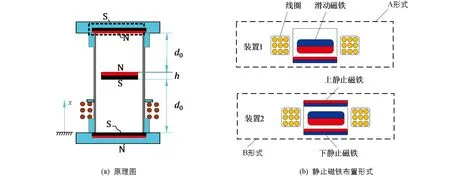
图5 振动能量俘获装置原理与磁铁布置图

基于Mann等[36]的研究成果,悬浮磁铁回复力为幂级函数,上静止磁铁回复力FU和下静止磁铁回复力FL为

(4)

(5)

其中：d0是图5(a)中静止磁体与悬浮磁体在静态平衡状态下的相对间距,m；x是悬浮磁铁相对于平衡位置移动的距离,m．

总回复力Fx表示为

Fx=FU-FL

(6)

代入公式(4)和(5)并展开,则有：

(7)

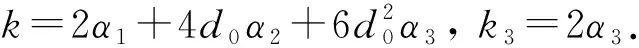
在振动能量俘获装置整体尺寸、悬浮磁铁和静止磁铁强度已知的前提下,同样激励条件下其能量俘获性能主要取决于静止磁铁和悬浮磁铁数量,但是难以通过改变悬浮磁铁数量改善能量俘获性能(多个悬浮磁铁串联增加磁场密度的同时增加了自身高度,导致悬浮磁铁最大运动幅值降低),因此,本研究主要探究振动能量俘获装置静止磁铁布置形式和数量对其能量俘获性能的影响,设计两种静止磁铁布置形式,分别命名为A形式和B形式,如图5(b)所示.基于有限元方法获得两种静止磁铁布置形式下悬浮磁铁的回复力,如图6所示．

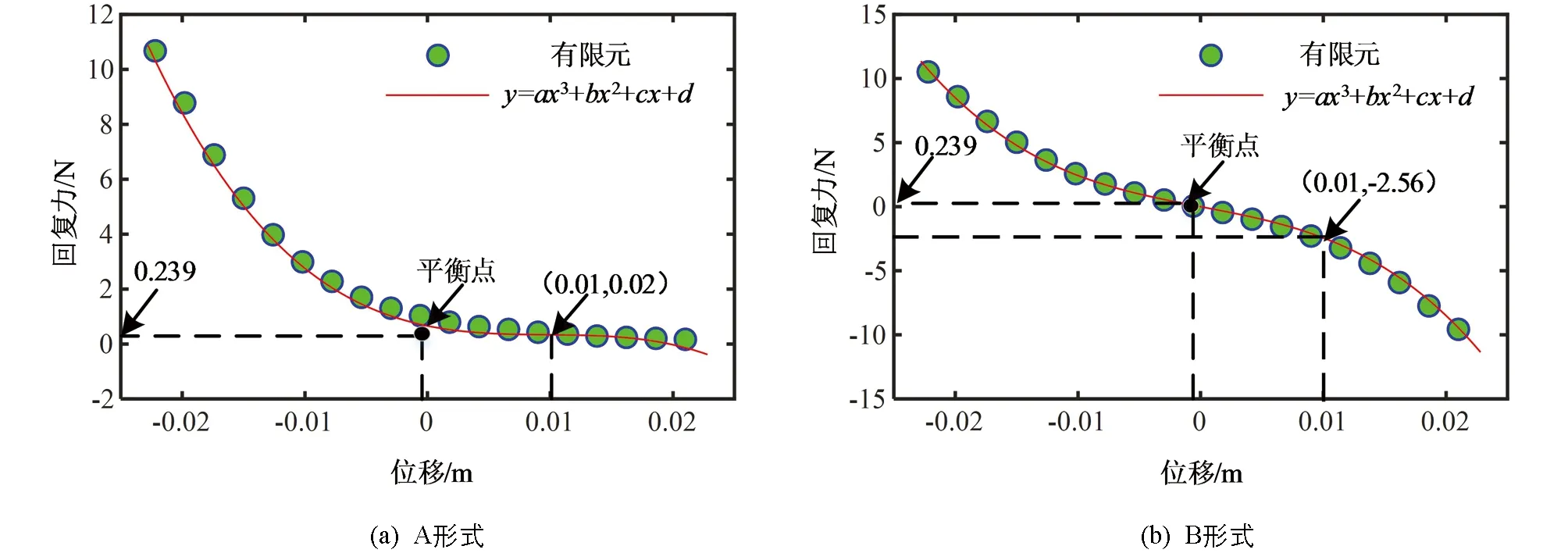
图6 悬浮磁铁在静止磁铁不同布置形式下的回复力

基于曲线拟合得到静止磁铁两种布置形式下悬浮磁铁回复力方程,A形式下的悬浮磁铁回复力方程为

Fx=-301 008x3+8 837.67x2-90.662x+0.66

(8)

B形式下的悬浮磁铁回复力方程为

Fx=-606 848x3-182.42x

(9)

由于悬浮磁铁自身质量(0.239 N)的影响,两种静止磁铁布置形式下的悬浮磁铁平衡点均在x轴负坐标.由图6(a)可以看出,下静止磁铁单独布置时,悬浮磁铁受到的回复力为单方向的,且回复力大小与悬浮磁铁和下静止磁铁之间距离成反比.由图6(b)可以看出,上、下静止磁铁均布置时,悬浮磁铁同时受来自上、下静止磁铁不同方向的回复力,且相对于位移0点呈近似对称关系.对比图6(a)和6(b)可以得到,悬浮磁铁同样的位移幅值,其受到的回复力变化值在A形式下小于B形式,如悬浮磁铁位移由0变化至0.01 m时,A形式下回复力变化约0.2N,而B形式下的回复力变化约为2.5N,证明了A形式下悬浮磁铁的刚度小于B形式,即在同样的激励下,A形式下悬浮磁铁切割磁感线的幅度和运动区间大于B形式,且前者的响应频率小于后者．

图7 道岔转辙机防护罩的限位

为了防止零件之间相互吸引作用降低磁浮系统能量转换能力,有机玻璃管采用不导磁树脂材料,除静止磁铁和悬浮磁铁外,其他部件均为不导磁的6061铝.实际安装过程中,道岔转辙机外壳为保护罩,保护罩的存在限制了振动能量俘获装置的结构尺寸与内部滑动磁铁数量,如图7所示.为了提高防护罩的抗压强度,增强防护罩与转辙机的贴合紧密度,降低防护罩成本,现有道岔转辙机防护罩内部可用空间较低,限制了本研究振动获能装置的尺寸设计.在满足轴销传感器工作所需能量前提下,振动能量俘获装置应尽可能简单和小巧(高度普遍不能超过80 mm),本设计振动能量俘获装置主要结构参数见表1．

表1 振动能量俘获装置主要结构参数

2 自供能传感器电路设计

图8为自供能传感器电路设计原理图.电路系统支持直流电源和交流电源,采用D1-D44个肖特基势垒二极管为交流电源的整流器.U1为开关控制和电源管理芯片,具有冷启动、异步升压和同步升压的分级式能量管理模式.功率电感器L1连接到升压调节器的开关节点(SW),模拟地(AGND)的裸露焊盘连接到电源地(PGND),4.7 μF电容器(C6)连接在输入电源(Vin)和电源地之间,另一个4.7 μF电容器(C2)连接在输出电源(SYS)和电源地之间,将超级电容器作为SYS输出电源的存储设备放置到BAT端,可以采用一个可选的备用输入电源,将其连接到引脚12,电容器C4连接在电容器旁路端口(CBP)和模拟地之间,采样并保持最大功率点电平.一个20 kΩ电阻器R7放置在引脚4上,以设置最小工作输入电压电平,CBP电压超过最小工作输入电压后,升压调节器开始切换.引脚5指示最大功率点跟踪电压,该引脚设置不同能量源的最大功率点跟踪电平．

上述电路系统具有3条电源路径.当系统输入电压大于电压启动阈值(0.38 V)且小于冷启动终止阈值时,系统为冷启动模式.当输出电压大于冷启动终止阈值且超级电容器电压小于关断放电电压(设置为2.4 V)时,升压调节器操作将SYS和BAT开关关闭,系统工作在异步升压模式.当输出电压和超级电容器电压大于关断放电电压,但小于存储过充电阈值(设置为3.6 V)时,升压调节器操作会打开SYS和BAT开关,以使能同步升压模式.具有外部电感器的开关模式同步升压调节器以脉冲频率模式工作,将存储在输入电容器中的能量转移到系统负载和能量存储单元(如超级电容器或可充电电池等).为了在较宽的输入功率范围内保持稳压器的高效率,采用内部颤振峰值电流限制策略以控制外部电感器的电流．

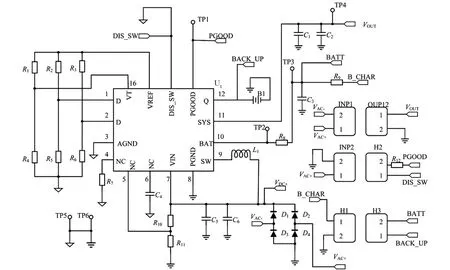
图8 自供能传感器电路原理图

图9 振动俘能试验布置图

3 自供能传感器性能试验

为了综合测试自供能传感器系统性能,特别是在中低频振动激励下的俘能性能,进行振动俘能装置正弦扫频和实际轨道振动工况下能量输出性能试验.图9所示为振动俘能试验布置图,主要包括振动俘能装置、电路模块、振动台、控制端、数据采集和储存装置,其中：振动能量俘获装置固定于振动台,电路模块的输入端与振动俘能装置连接,电路模块的输出端则与数据采集装置连接,数据采集装置采集的数据保存至数据存储装置．

3.1 轮轨交互作用下的钢轨振动俘能测试流程

由于轨道交通的特殊性,难以频繁开展上道验证试验,因此多采用室内试验模拟真实轨道工况.利用前期布置传感器获取列车通过时轮轨交互作用下的钢轨振动加速度数据,然后将获取的钢轨振动加速度信号转换为速度信号后导入控制器,控制器基于速度控制策略通过控制功率放大器驱动电磁激振器按照轨道谱的振动速度时程曲线动作,进而同与之固定的振动台台面协同上下振动,速度传感器读取振动台台面的速度信息并反馈给控制器,实现轨道谱随机振动信号的精确控制.同时,利用示波器采集振动能量俘获装置输出的电压响应,最后对示波器数据进行读取、滤波与分析,如图10所示．

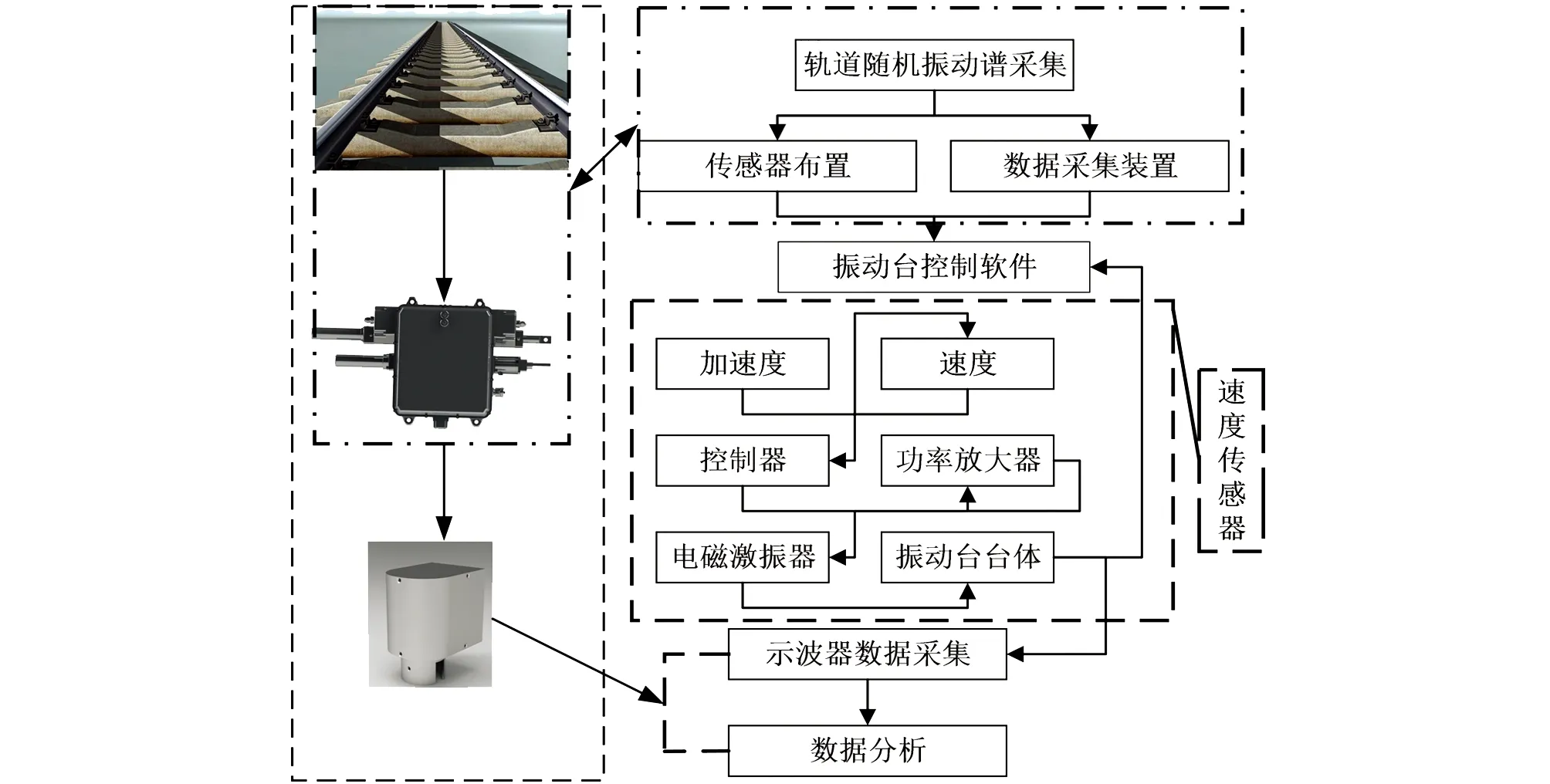
图10 轮轨交互作用下的钢轨振动俘能测试流程图

3.2 加速度与速度之间转换验证

振动能量俘获装置核心部件悬浮磁铁滑动速度正相关于发电电压,这与振动速度密切相关.而且,对于常用振动台来讲,由于受加速度传感器、电磁力、设计尺寸和振动俘能装置重力的影响,其加速度超限概率远大于速度超限,因此,需要采用将加速度传感器获取的随机振动信号进行积分转换为速度曲线后的速度控制策略.为了验证基于加速度推导获取速度信号与原始速度信号的拟合度,给定一标准正弦速度曲线作为对照曲线,即图11(a)中蓝色曲线； 其加速度曲线为图11(b)中黄色曲线,方程为

α=-ω2Asinωt

(10)

其中：α为加速度,m/s2；A为振幅,m；ω为角速度,rad/s；t为时间,s．

如图11所示,对给定正弦曲线加速度积分可以获得基于积分方法的速度曲线(红色曲线),积分速度曲线和对照速度曲线均为趋势一致的正弦曲线,但是二者之间有偏差； 对照速度曲线和积分速度曲线之间的偏差为对照速度曲线的初速度,即时间为0时的初始启动速度； 积分正弦速度曲线叠加初速度进行修正后的曲线与对照速度曲线重合,图11(a)表明了标准正弦加速度振动曲线积分获得速度曲线的合理性.但是实际的轨道振动信号包含了噪声,将高斯白噪声曲线(亮青色曲线)施加于已知正弦加速度曲线(黄色曲线)得到加速度曲线(黑色曲线),由于噪声的存在,必须将加速度曲线进行滤波降噪后积分,滤波后积分的速度曲线(绿色曲线)与已知正弦速度曲线基本吻合,如图11(b)所示,证明了利用积分法推导随机振动加速度信号的有效性．

3.3 正弦扫频试验

为了验证所设计自供能传感器振动能量俘获装置是否能够在宽带频率下获得足够的电能,并探究上、下静止磁铁布置形式对能量俘获特性的影响,再进行7次不同工况下的正弦扫频试验,其中：频率为5～50 Hz,振幅为1～7 mm,加速度为20 m/s2.通过对实际扫描频率信号中各频率的峰、谷电压进行分析,将采样时间变换为采样点,利用微分方法可以求出所有的峰和谷.具体来说,所有的信号都可以通过对真实扫描频率信号的微分得到.在某个采样点上,如果正号变成负号,拐点就是峰,反之就是谷,二者的差值为峰峰值.正弦扫频试验的结果如图12所示．

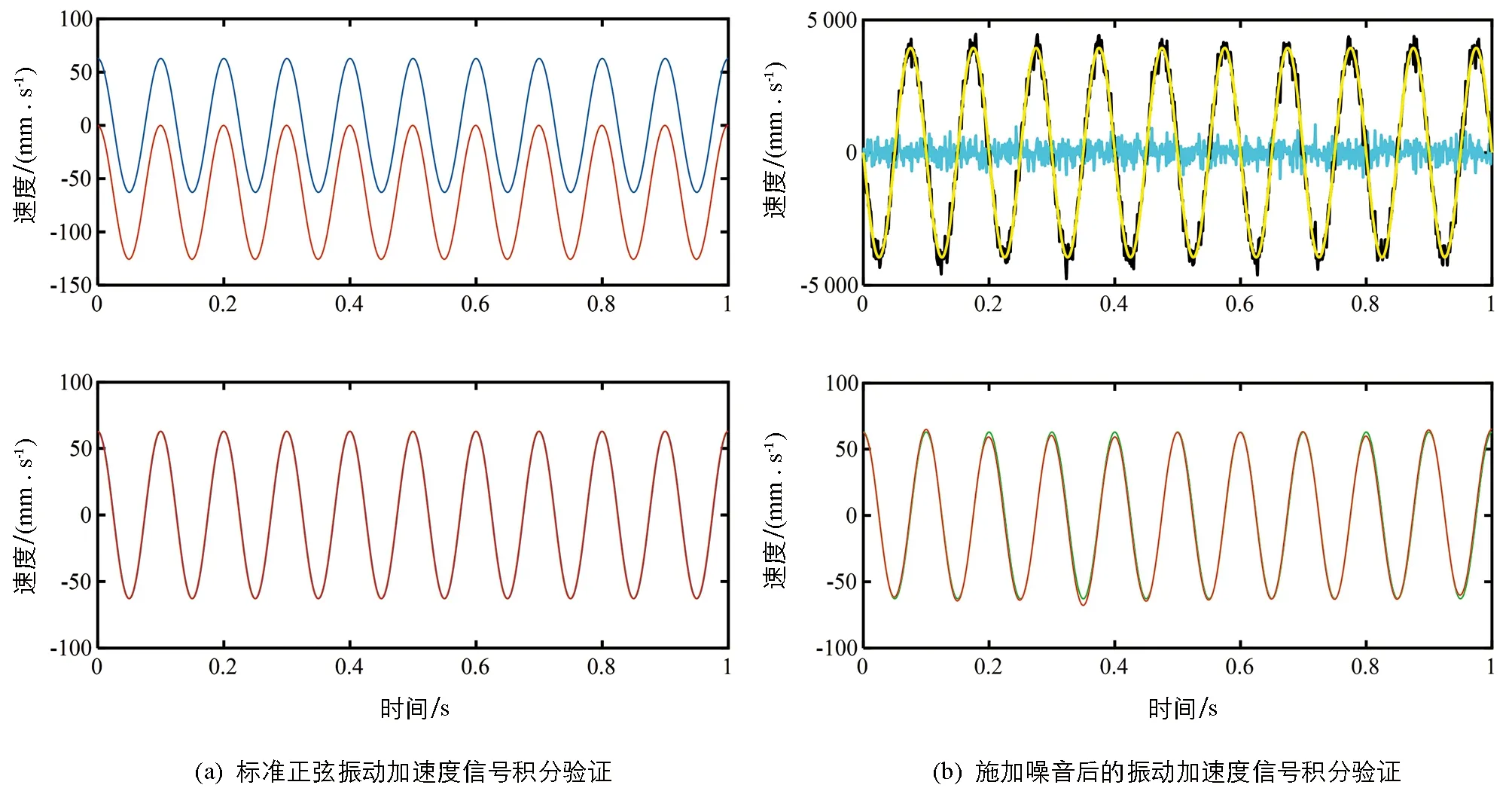
图11 加速度与速度之间转换与验证

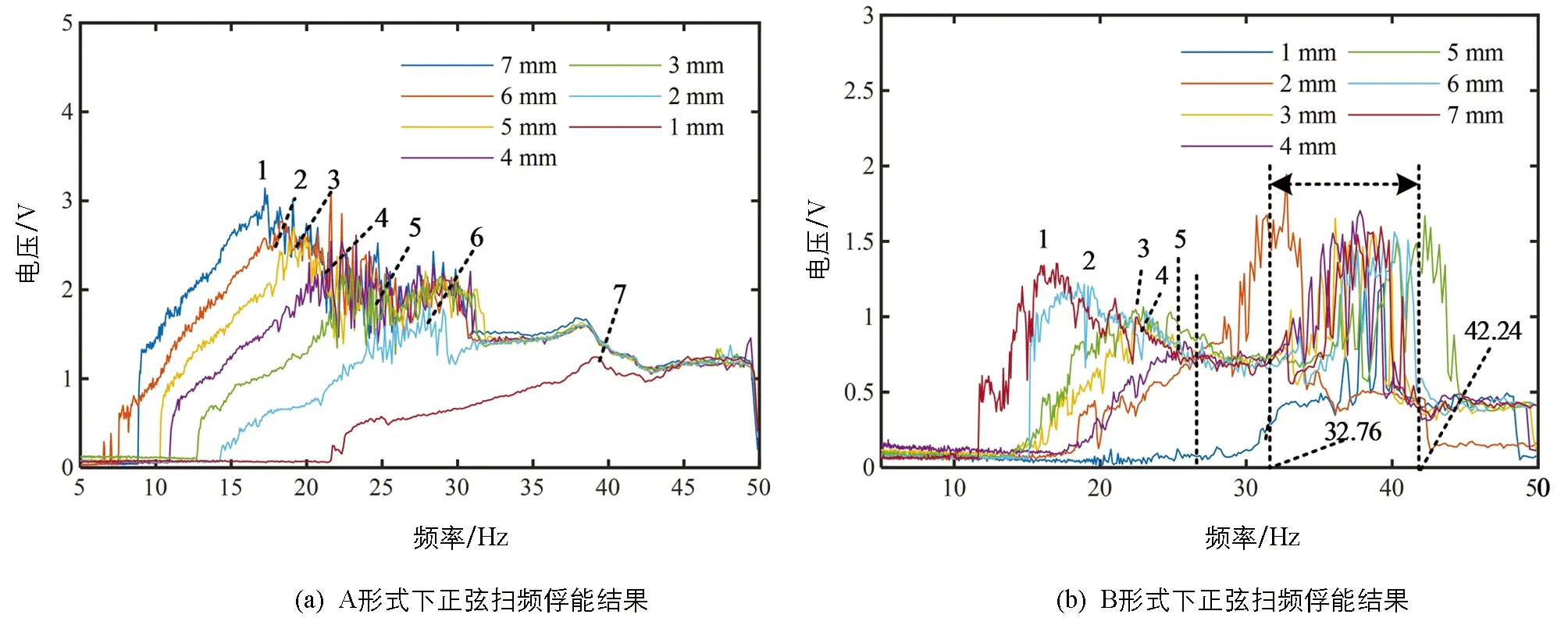
图12 振动俘能装置正弦扫频结果

由图12(a)可以看出,当静止磁铁布置形式为A形式时,振动能量俘获装置只有一个极值,分别用数字1～7标识,极值对应的频率与电压分别为：7 mm(17.23 Hz,3.142 V),6 mm(18.39 Hz,2.767 V),5 mm(19.17 Hz,2.722 V),4 mm(21.61 Hz,2.545 V),3 mm(23.38 Hz,2.152 V),2 mm(28.13 Hz,1.849 V),1 mm(39.23 Hz,1.243 V),即极值对应的频率随着正弦扫频激励振幅的增大而减小,而极值对应的电压幅值却随着振幅的增大而增大； 当静止磁铁布置形式为B形式时,振动能量俘获装置极值分布情况为：正弦激励振幅为3～7 mm时存在两个极值,第一个极值在图12(b)中以1～5标识,对应的频率与电压分别为：3 mm(27.76 Hz,0.836 V),4 mm(22.32 Hz,1.029 V),5 mm(21.02 Hz,1.121 V),6 mm(18.9 Hz,1.215 V),7 mm(17.02 Hz,1.354 V),第二个极值点对应的电压均为1.6 V左右,而对应的频率范围为32.76～42.24 Hz.正弦激励振幅为1 mm和2 mm时只有一个明显的极值．

由图12可以看出,电压曲线在约30 Hz之后逐渐重合.理想情况下,振动台输出的激励应始终保持恒定的加速度,但是,扫频的初始阶段频率较低,保持恒定的加速度需要较大的位移,而大多数振动台对其最大位移有严格的限制,因此,振动台在初始阶段输出固定位移激励,然后输出固定加速度激励,两种激励模式切换的频率定义为交越频率,且交越频率随着最大位移的减小而增大.正弦扫频测试中,所有激励都具有相同的加速度,但最大位移不同,所有的激励在通过交越频率后会有相同的激励,即所有激励在交越频率后都是相同的,因此,输出电压在约30 Hz后的曲线几乎都是重合的．

综上所述,振动能量俘获装置静止磁铁布置形式为A和B时均在较宽的频带内具有优异的俘能性能.但A形式下振动能量俘获装置极值对应的响应频率低于形式B,在较低的响应频率下获得最佳性能,而形式B则在相对较高的频率下获得较优的性能,这是由于A形式下振动能量俘获装置的刚性小于形式B,这与图6分析结果一致.同等激励下,A形式下振动能量俘获装置电压高于B形式,这是由于A形式下悬浮磁铁运动幅度和切割磁感线范围大于形式B,这也与图6分析结果一致,而B形式下,振动能量俘获装置出现2个极值则反映了此形式下悬浮磁铁运动的非线性特性．

3.4 实际轨道振动谱激励下的俘能测试

道岔转辙机作用于道岔实现车辆转向,道岔结构复杂,不仅体现于其轨线布置和走行线路转换环节,更在于其多变的轮轨关系,导致道岔与车轮的相互作用程度及磨耗大于普通轨道[37].钢轨包括普通线路和磨耗线路,道岔则是轨道结构的薄弱环节,3种线路结构的钢轨振动试验能表征轨道振动的典型工况,因此有必要在无磨耗钢轨、有磨耗钢轨和道岔振动谱激励下进行自供能传感器振动俘能系统性能检验．

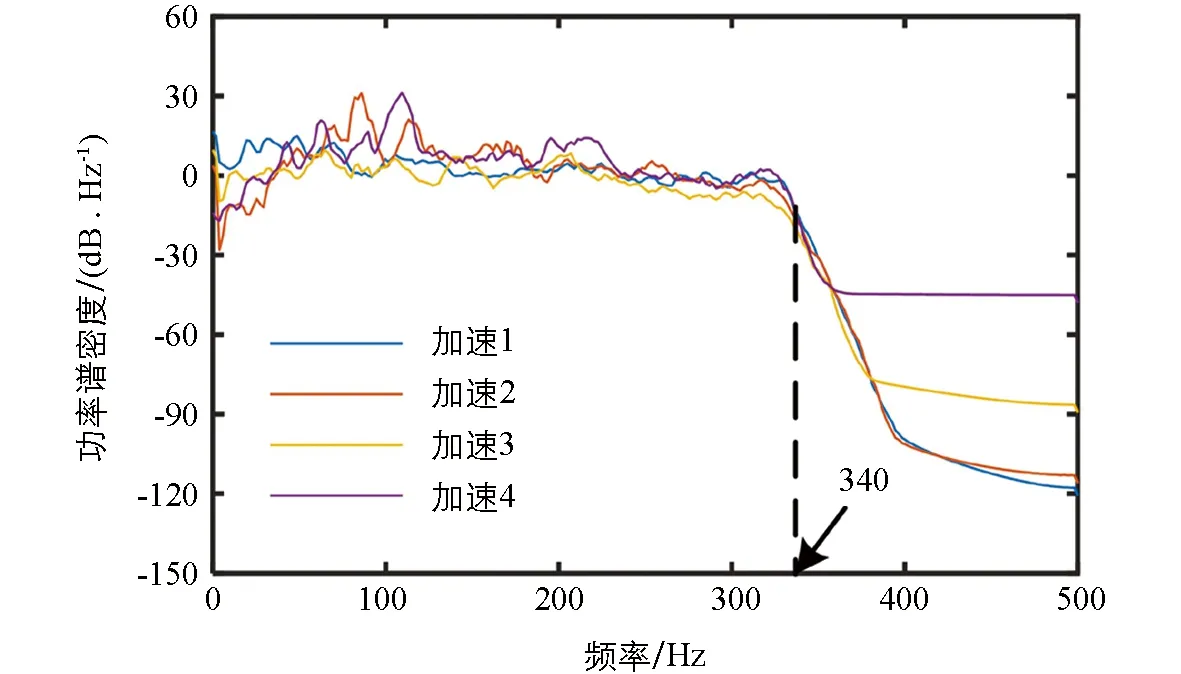
图13 实测钢轨振动信号功率谱密度

3.4.1 钢轨振动谱激励下的俘能测试

选取前期采集到的4种钢轨加速度信号,包括钢轨有磨耗和无磨耗各2种.4种钢轨振动信号的功率谱密度如图13所示,振动信号主要集中在低于340 Hz的中低频率,且列车通过有磨耗的钢轨时加速度和速度极值均高于钢轨无磨耗状态.将加速度信号转换为速度信号并导入控制器进行基于速度控制的俘能测试．

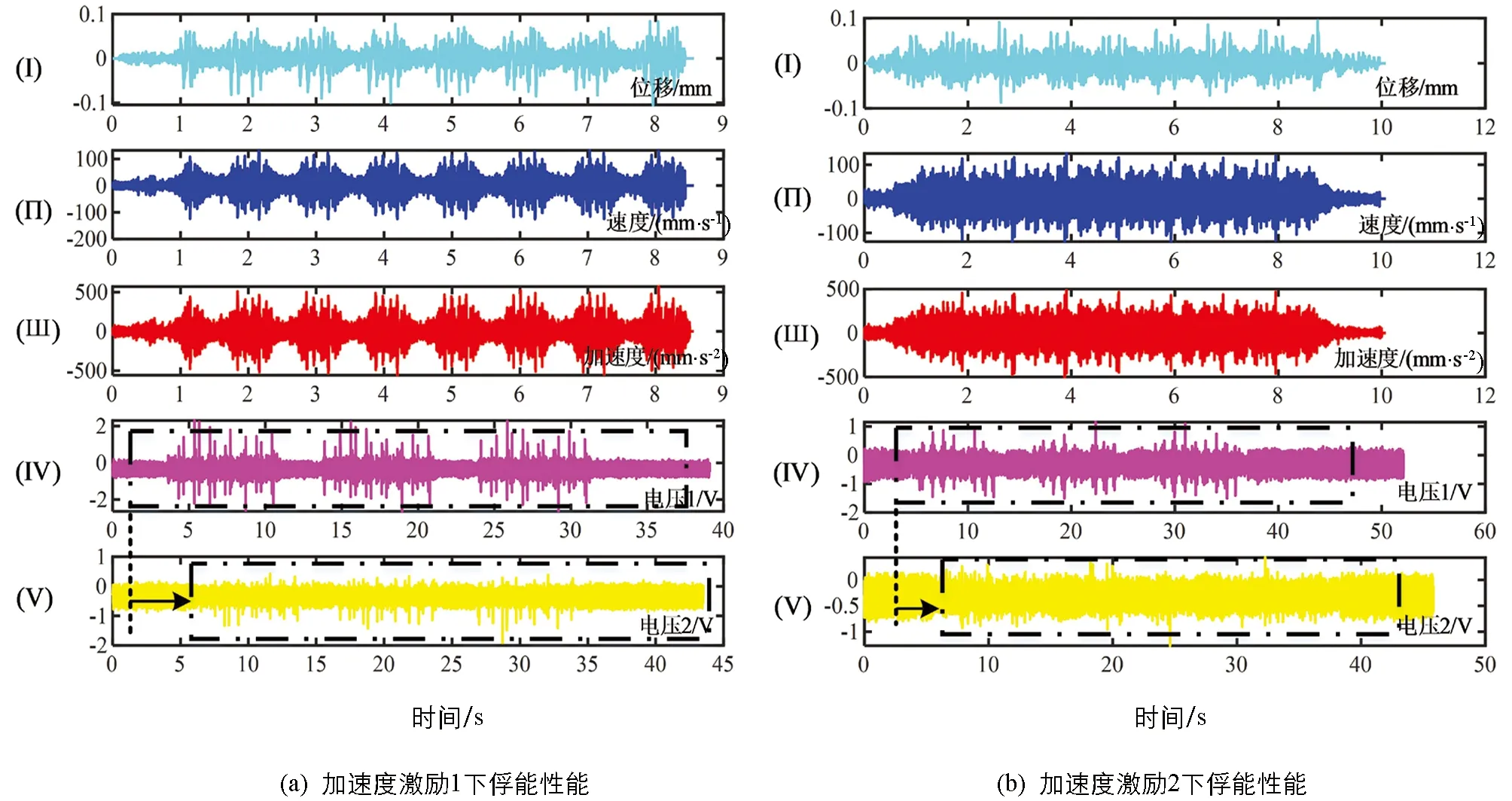
图14 有磨耗激励下振动俘能系统性能测试

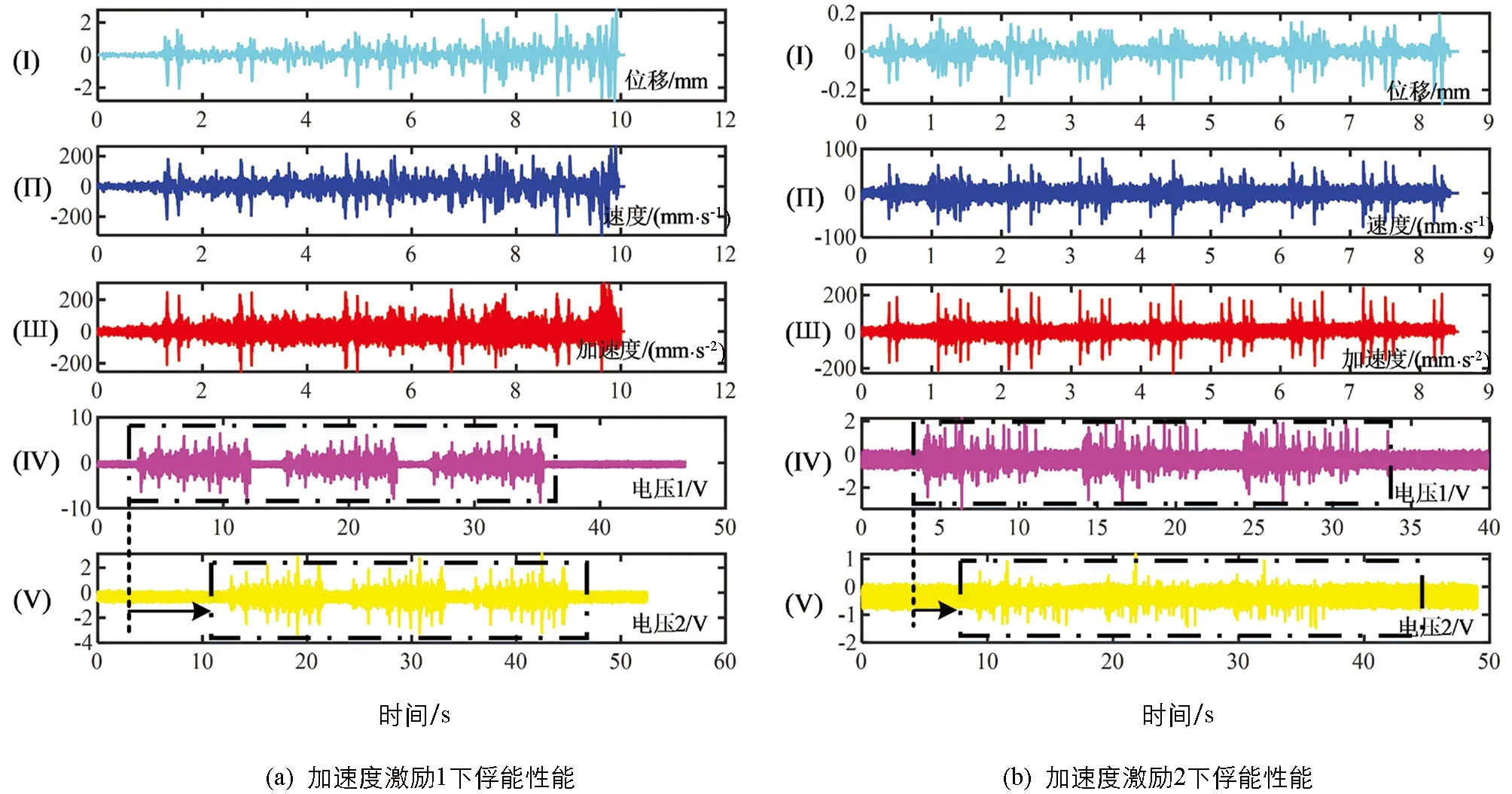
图15 无磨耗激励下振动俘能系统性能测试

钢轨无磨耗激励下,静止磁铁布置形式为A和B的振动俘能装置在加速度激励1和2下的俘能电压最大幅值分别约为5，2.5，2.5，1 V,如图15所示.振动俘能装置静止磁铁布置形式为A时的俘能电压大于B形式,且布置B形式时振动俘能装置俘获电压优异的区间相对于A形式整体右移,更倾向于相对频率较高的频带,这与图6、图12和图14分析结果一致； 静止磁铁同等布置时,图15(a)所输入激励下振动俘能装置俘获电压的能力均大于图15(b)所输入激励下的俘获电压,虽然两种激励下加速度极值均为250 m/s2,且难以快速直观地分辨两种随机激励下二者速度变化率大小,但是图15(a)激励下的位移幅值为1 mm,大于图15(b)激励下的位移幅值(0.25 mm)．

图14和图15反映了在小振动位移(<1 mm)、宽振动频率(≤500 Hz)、轨道有磨耗或无磨耗激励下振动俘能装置均能够俘获不低于1 V的电压,能够满足自供能传感器电路的启动和备用电池充电要求,可以作为道岔转辙机轴销传感器的供能电源.史玉杰等[38]建立了道岔转换设备的分析模型,给出了道岔转换装置的前三阶主振频率,分别为11.3，262.88，846.50 Hz,并给出了实测的车速为80 km/h时,转换装置的最大振动位移约为3.7 mm.李烨峰[39]根据大秦重载铁路12号道岔动力性能测试数据显示,当列车直线过岔时,道岔部件最大位移变形为1.26 mm,而当列车侧向过岔时,道岔部件最大位移变形为2.96 mm.可见本研究提出振动俘能装置正常工作时所需要的最小位移能够得到满足,且工作频带可以覆盖转换装置前两阶主振频率．

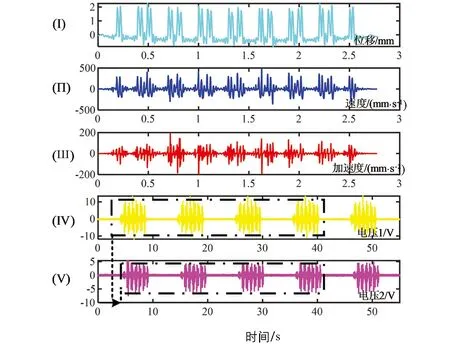
图16 道岔振动谱激励下振动俘能系统性能测试

3.4.2 道岔振动谱激励下的俘能测试

道岔振动谱采集自国内某高铁站8节编组客车驶过时道岔翼轨的垂向振动,其最大振动位移、速度和加速度分别为2 mm，500 mm/s和200 mm/s2,如图16-所示．

4 结论

本研究针对高速铁路轨道结构薄弱环节道岔转辙机拉力监测与能量供给问题,设计了一种自供能传感器系统,系统包括振动能量俘获装置、轴销传感器和电路.基于道岔转辙机实际尺寸,确定了轴销传感器和振动俘能器的结构与尺寸,并借助速度控制策略,通过正弦扫频和轮轨交互作用下的轨道振动俘能试验,验证了自供能传感器振动俘能装置的性能.主要结论如下：

1) 轴销传感器本身既是结构紧固件又是传感器,能够实时记录自身所受拉压力的变化,其参数为：额定载荷F=10 000 N,输入3～6 V,输出1.5～2 mV/V,满足实际使用所需的5 000 N拉力检测要求,自供能传感器电路可以在低感应电压下工作,启动电压为380 mV．

2) 基于正弦扫频试验测试了两种静止磁铁布置形式下自供能传感器能量俘获性能.相对于上、下静止磁铁均布的形式,只有下静止磁铁布置的振动俘能装置悬浮磁铁刚度更低,能够在同等激励下获得更大的切割磁感线范围和运动幅值.因此,单静止磁铁布置下的振动俘能装置可以获得更高的感应电压幅值,但是其响应频率和频带低于上、下静止磁铁均布的情况．

3) 基于速度控制策略实现了有磨耗钢轨、无磨耗钢轨和道岔振动谱激励下自供能传感器俘能性能试验,验证了静止磁铁不同布置形式下其响应频率和俘能特性,证明了在小振动位移幅值(<1 mm)、宽振动频率(≤500 Hz)、轨道有磨耗、无磨耗和道岔振动激励下自供能传感器均能够输出幅值不低于1 V的电压,能够满足电路的启动并对备用电池充电,可满足道岔转辙机自供能传感器的功耗需求．