单管无线电能传输逆变系统纹波抑制研究

杨奕， 张学健， 罗蕾， 谢诗云， 叶庆

1. 重庆理工大学 电气与电子工程学院,重庆 400054； 2. 重庆市能源互联网工程技术研究中心,重庆 400054

近年来,桥式和推挽式拓扑结构使电子产品变得过于庞大和昂贵,无法用于手机和智能可穿戴设备的电能传输,因此,小功率电器的充电器可以采用单管逆变拓扑电路[1-3].由于传统单管无线电能传输逆变系统输入电流会突变至零,严重影响直流电源使用时长和系统传输效率,因此提出了一种隔直型拓扑无线电能传输发射端电路,此电路能够有效改善输入电流波形,提高系统效率[4-8].系统高频逆变单元采用单管功率放大,与全桥逆变电路相比,单开关管能够提升更大的输入电压值,同时还能够满足零电压开关,减小系统开关损耗,达到最佳瞬态响应状态[9]．

1 系统结构及工作过程

如图1所示,系统由驱动电路、逆变电路、整流电路、滤波电路和DC-DC变换器构成[10-11].通过单片机产生PWM波控制高频开关管的通断从而使发射端电感电容谐振消除无功功率,将能量尽可能地耦合到接收端,接收端电感电容谐振消除无功损耗,使电路效率达到最高再提供给负载使用[12-14]．

隔直型发射端并联谐振原理图如图2所示,图中C1为补偿电容,L1为谐振电感,VT1为开关管.该发射端电路的工作模态图如图3所示.图4为传统发射端并联谐振拓扑图,图中C2为补偿电容,L2为谐振电感,VT2为开关管[15],该发射端电路的工作模态图如图5所示．

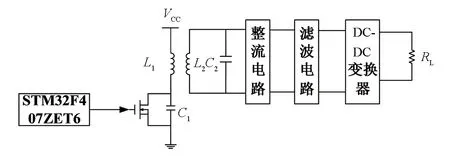
图1 系统结构框图

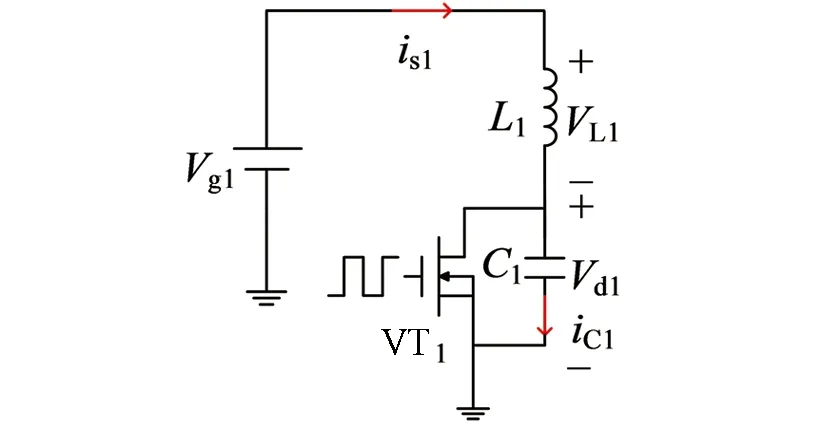
图2 隔直型发射端并联谐振原理图

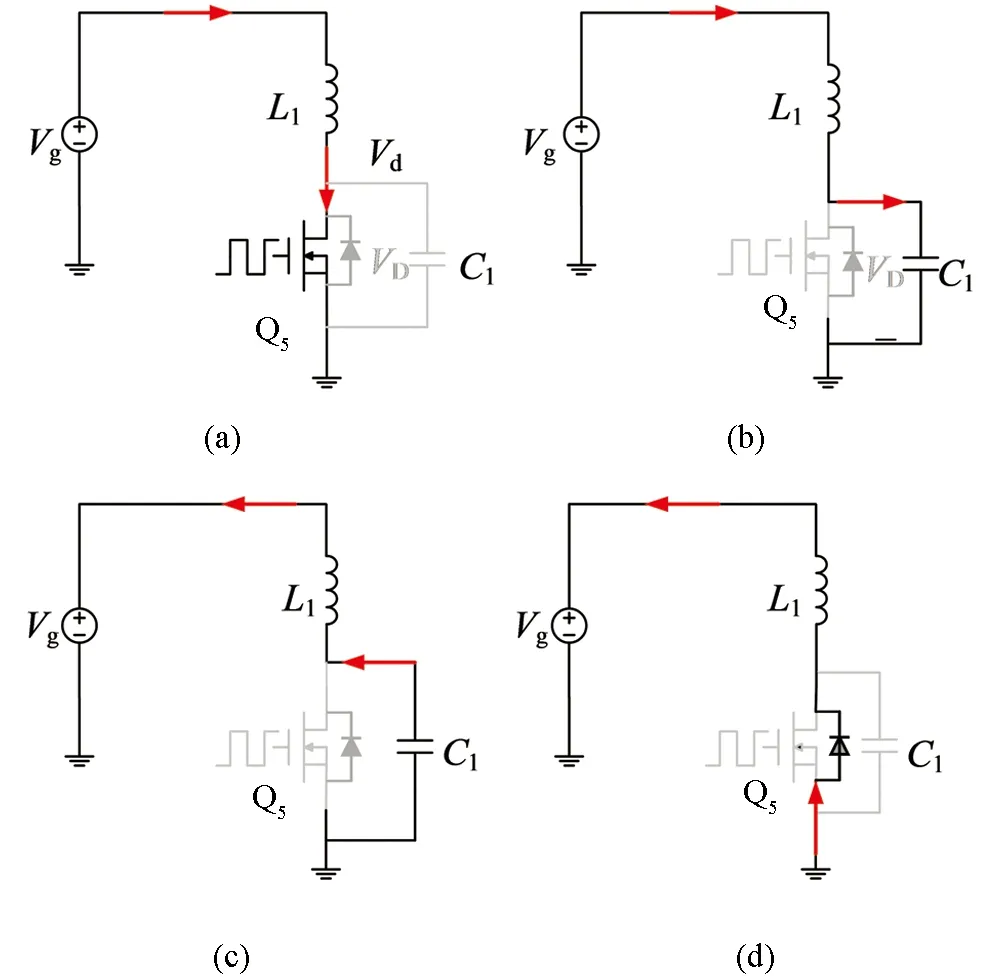
图3 隔直型发射端工作模态图

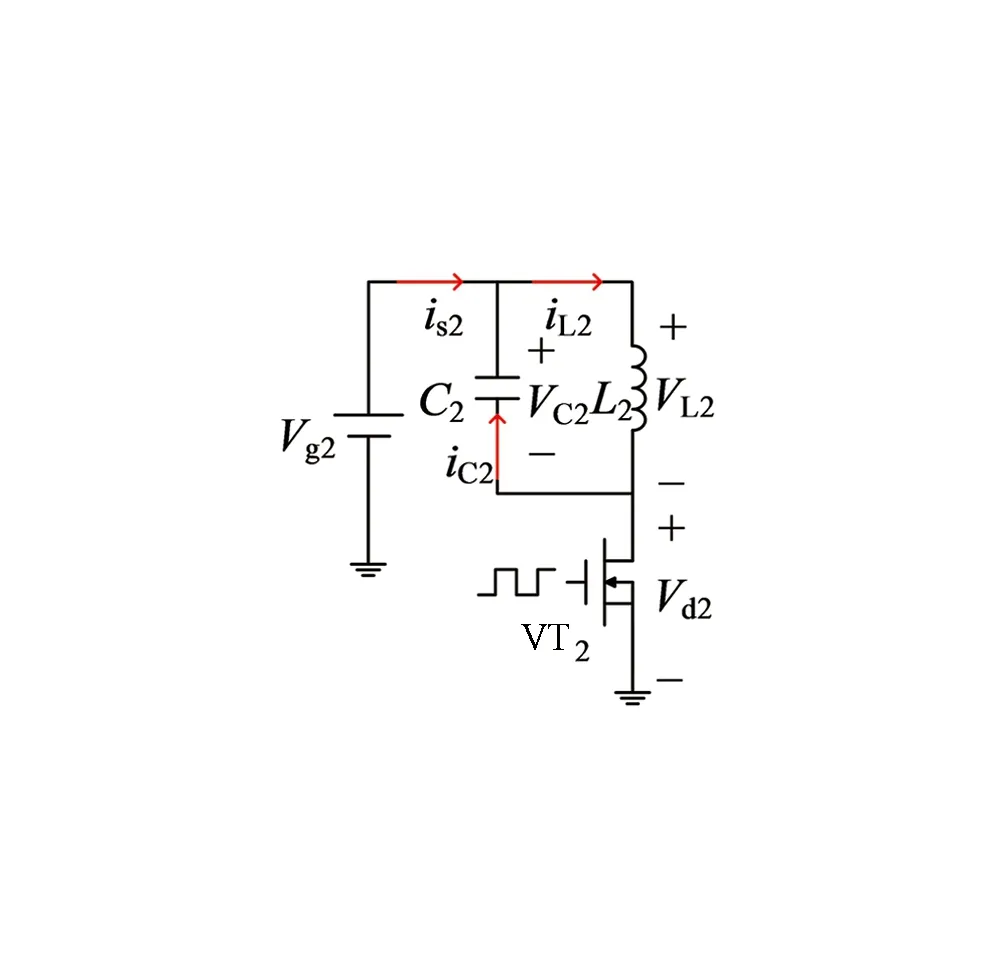
图4 传统发射端并联谐振拓扑

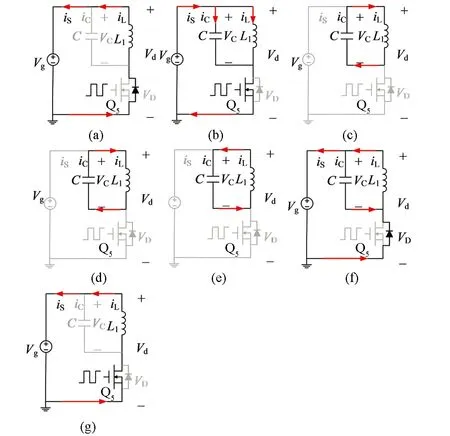
图5 传统发射端工作模态图

其中隔直型拓扑的模态分析如图3[15-16]：

阶段1：开关管导通,iL1线性增加； 阶段2：开关管关闭,iL1减小,C1积累电荷； 阶段3：开关管关闭,电容向电感充电； 阶段4：开关管零电压导通,电感电流通过续流二极管续流,降低至零,重复阶段1．

2 隔直型拓扑电路模型分析

放大电路直流和交流总是相互存在,分为直流通路和交流通路,在直流路径中,电容器断开连接,电感器短路,而交流路径中交流信号源短路,电容直流电源短路[17-19]．

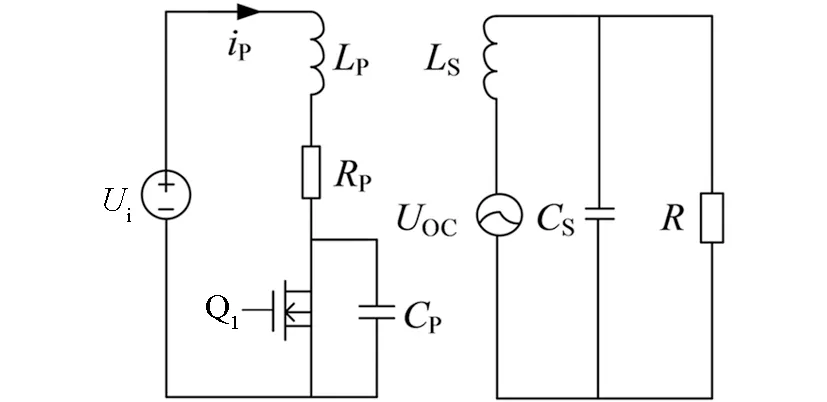
图6 原副边等效电路图

如图6所示为等效电路模型[20-22],其中LP为等效电感,RP为等效电阻,UOC为副边的开路电压,IP为电感电流,LS为副边电感,CS为副边补偿电容,R为等效负载,RL为图1所示系统的真实负载．

副边等效阻抗是：

可以得到副边等效到原边的反映阻抗为

(1)

其中ω为角频率,M是原线圈和副线圈之间的互感.由式(1)可知LP=L1+XP/ω,其中L1是图1系统中的真实电感值,由隔直型模态阶段1可知,开关导通电容CP被短路,电感L1处于充电状态且初始时刻电流为0,根据基尔霍夫电压定律可知：

(2)

由式(2),[t0,t1]内流过电感的电流是：

(3)

其中电感L1的电流峰值为

(4)

其中D为开关管占空比,T为运行周期.当开关管关断时,电感L1和电容C1就会发生谐振,由基尔霍夫电压定律和电流定律可知：

(5)

令iP(t1)=IPmax,uCP(t1)=Ui,解得流过电感L1的电流及两端电压为

(6)

其中

由上式可知,流过电容CP的电流ICP为

(7)

如图2所示,对于隔直型拓扑发射端并联谐振电路而言,输入电流IS1等于电感L1中流过的电流：

(8)

根据KCL,输入的总电流IS2是电容上通过的电流与电感上流过的电流之和：

(9)

3 仿真分析3.1 关于输入电流的仿真分析

为了验证所提出的隔直型拓扑发射端电路的有效性和可行性,使用MATLAB对隔直型和传统型两种电路分别进行了仿真分析.根据PP型无线电能传输系统的工作原理,计算得出系统电路仿真主要参数如表1所示．

表1 仿真主要参数

模型主要分析发射端电路中各器件的波形变化.设置输入电压为12 V,传统并联谐振发射端电路中补偿电容为0.094 μF,隔直型拓扑发射端电路中,滤波电容与补偿电容均设置为0.047 μF．

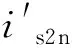
从图7中我们能够发现is1n和is2n两组仿真波形与理论模型推导得出的波形相同,谐振单元的输入电流波形有些差异.由图8可知,在初始时间段即电感L1处于充电状态时两种电路的输入电路波形没有太大差别,这是因为此时开关管导通电容被短路,所以电容电流为零.对于传统并联谐振电路而言,这个时间段内输入电流is2n等于电感电流iL2,当电路进入谐振阶段,开关管断开,电容与电感之间能量交换产生谐振,输入电流等于零.但是隔直型并联谐振电路输入电流is1n一直等于电感电流iL1,电流波形更平滑．

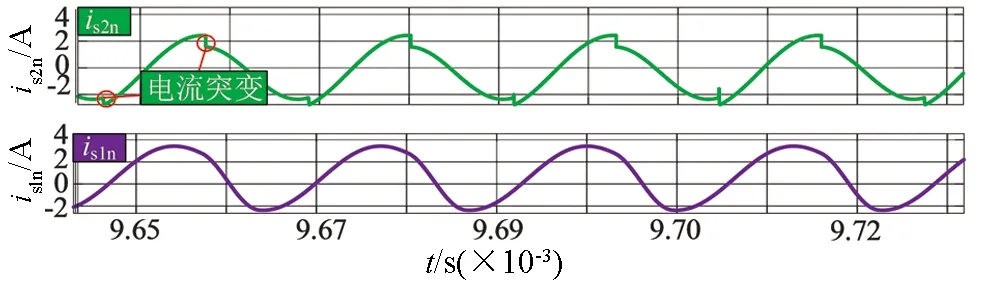
图7 实际工程中静态模式下两种电路输入电流波形

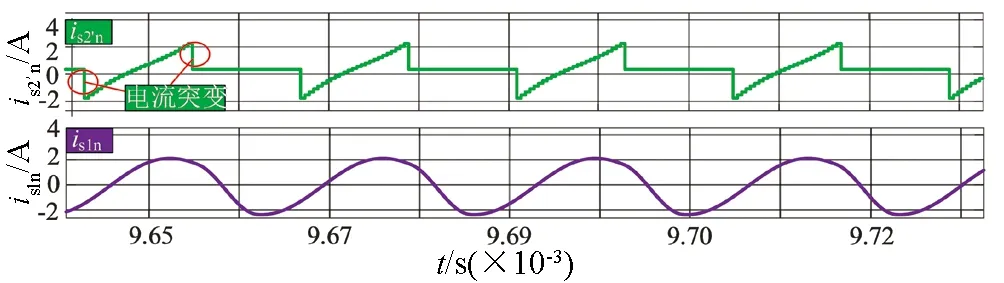
图8 理想情况中静态模式下两种电路输入电流波形图

图9是实际工程中在带载条件下分别对两种电路进行的仿真,图10是理想情况中带载条件下分别对两种电路进行的仿真.从仿真波形可以看出,传统的并联谐振电路加入负载后,电源端输入电流波形发生了突变,且由于电路中存在大量的电荷无法释放导致了极大的电流冲击.而隔直型拓扑电路的输入电流波形与谐振电感波形相同,可见隔直型拓扑带载能力比传统型拓扑更强．

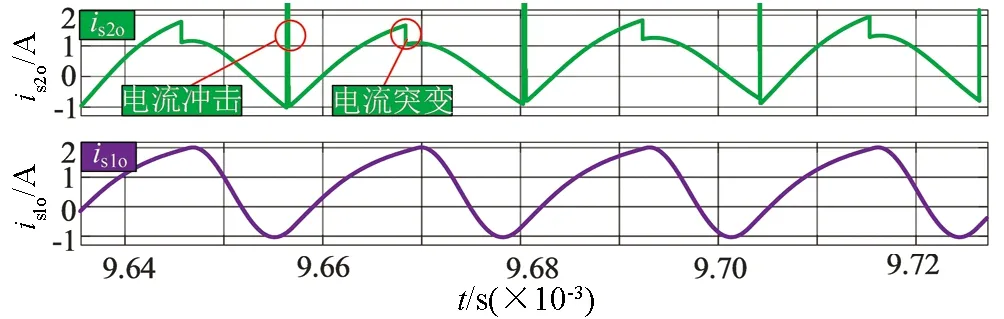
图9 实际工程中带载模式下两种电路输入电流波形

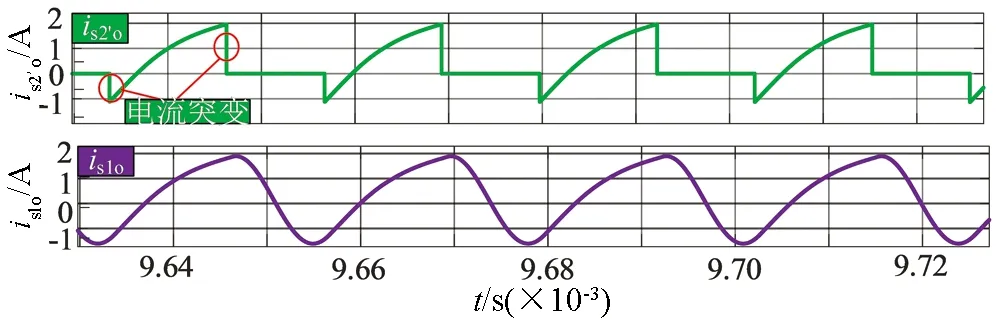
图10 理想带载模式下两种电路输入电流波形图

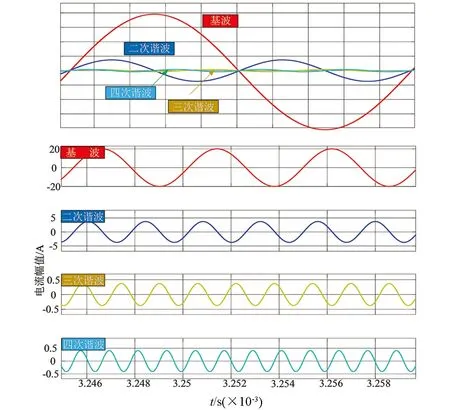
图11 输入电流傅里叶分解波形

3.2 关于纹波抑制的仿真分析

为更好对输入电流纹波抑制做出分析,将输入电流进行傅里叶分解(图11),图12所示为三次谐波两路180°移相后的波形合成,可见三次谐波在合成后的值几乎为零．

单管逆变系统输入电流的纹波无法消除,纹波对整个系统的稳定造成了严重的影响[16]．

关于无线电能传输纹波抑制相关文献记载有限,在基尔霍夫电流定律的基础上采用发射端并联输出端串联拓扑.以3个发射端并联移相为例(图13),3个模块参数相同,具体仿真参数见表1．

图14(a)的三维散点图显示了相移角度、开关频率和电流峰值之间的相关性.移相角度范围为[10°,350°],开关频率为[186 k,237 k],在移相角[110°,130°]内和切换频率为[196 k,216 k]时电流峰值处

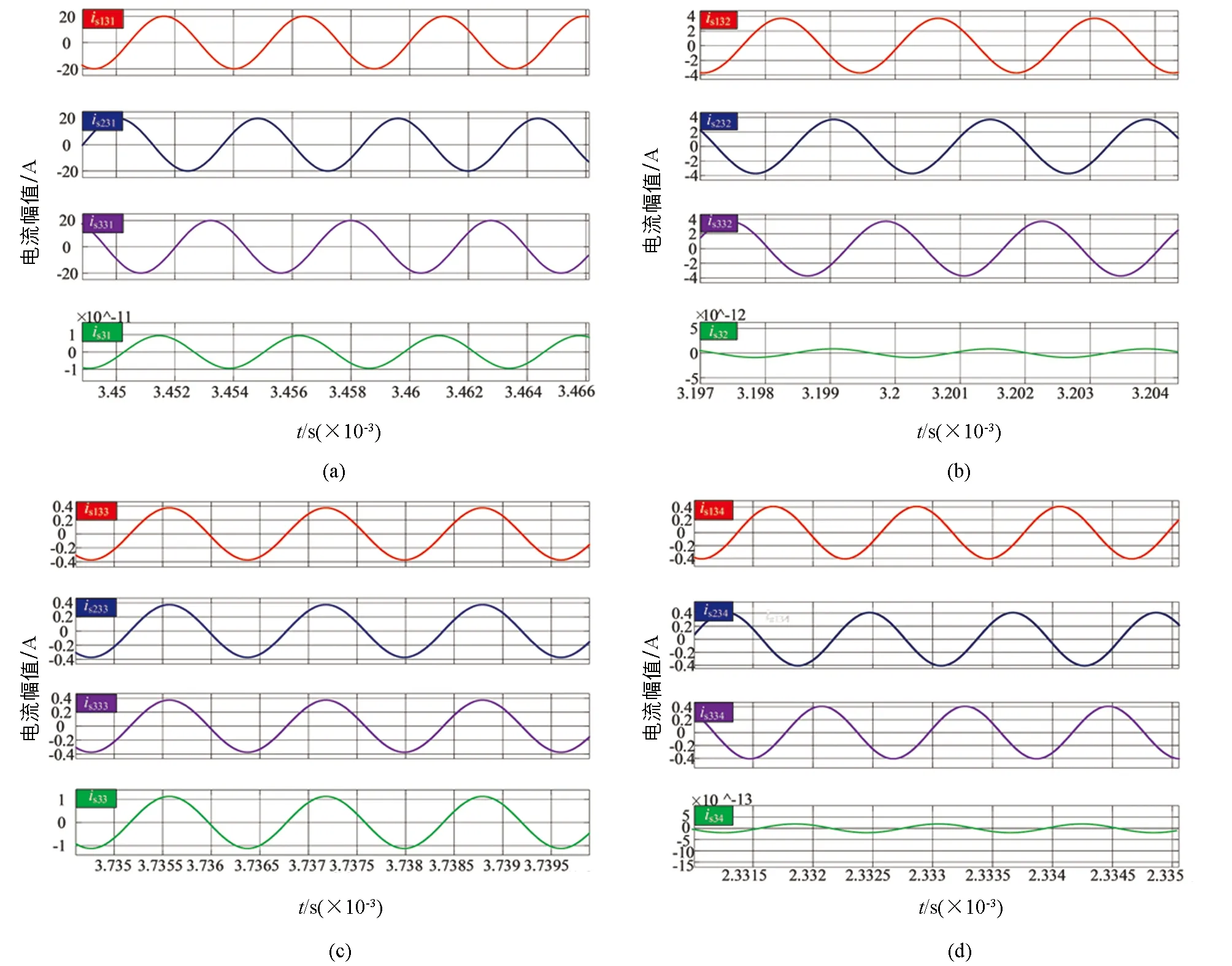
图12 三相交错并联移相波形叠加图

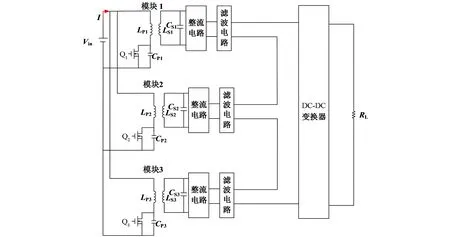
图13 三路移相拓扑图

于谷值状态,电流峰值随着相移角和频率的增加而上升.为了进一步分析相关性并找到相移和频率的最佳点,图14(b)制作了一个三维散点图,图中移相角为[110°,130°],频率为[196 k,216 k],可见移相120°角处,频率为206 k,电流峰值最小．

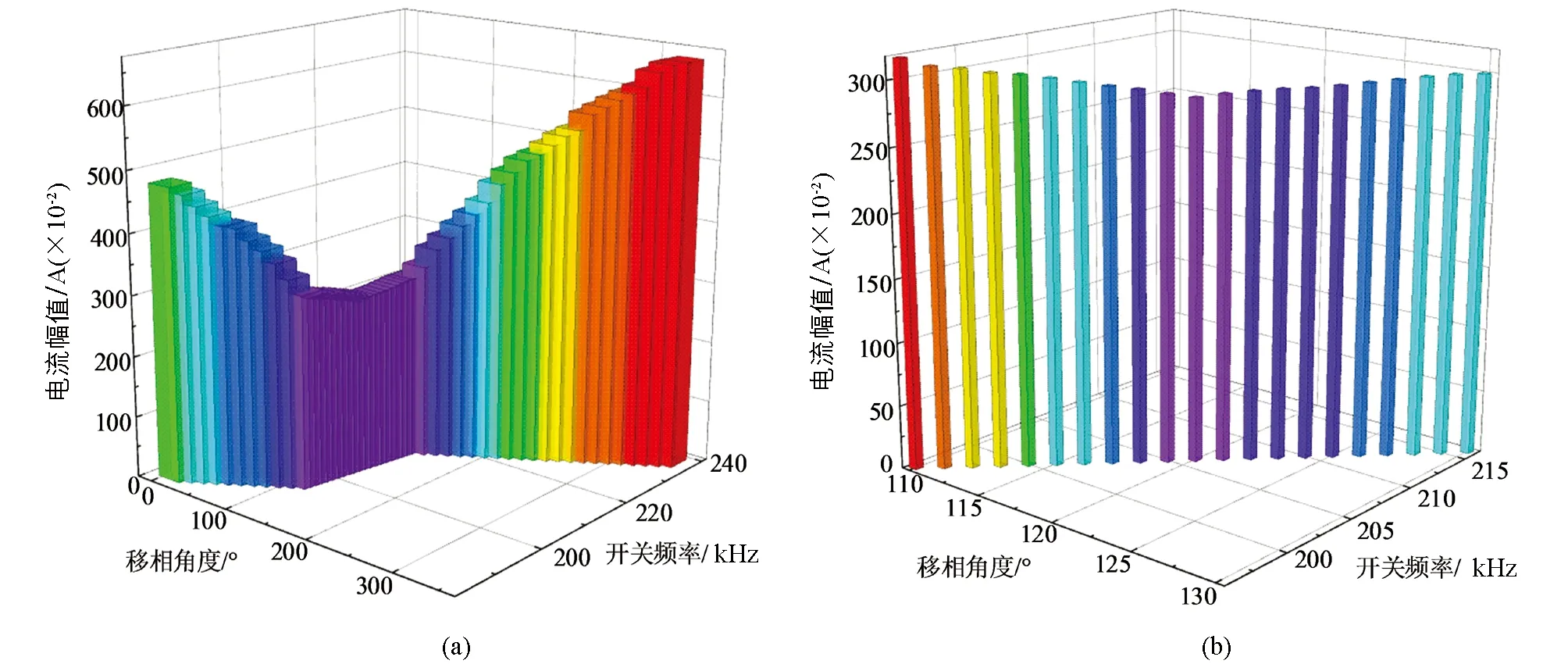
图14 电流幅值与移相角度和开关频率之间的关系

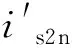
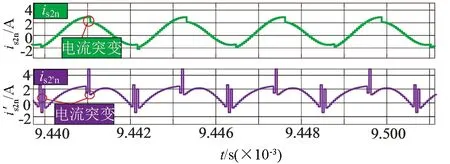
图15 传统型拓扑静态120°移相输入电流波形图

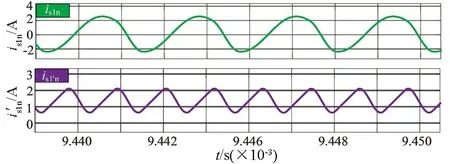
图16 隔直型拓扑静态120°移相输入电流波形图

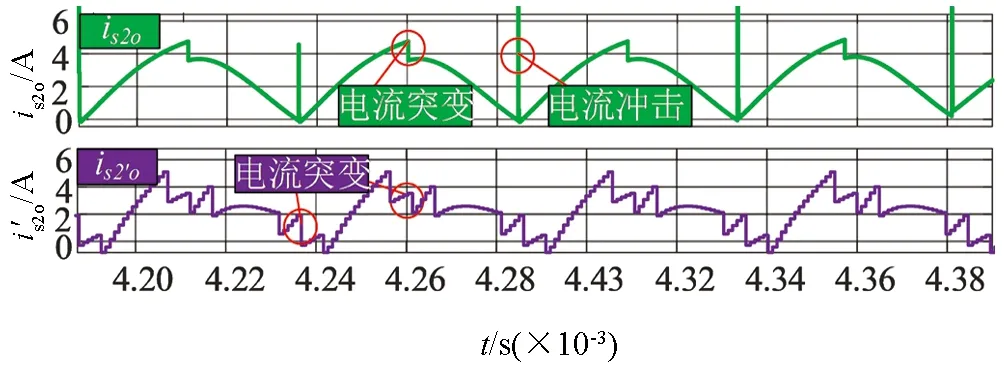
图17 传统型拓扑带载120°移相输入电流波形图

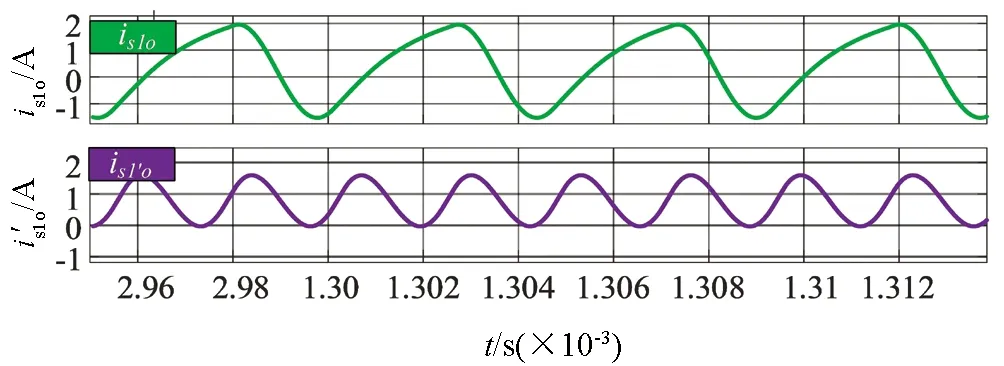
图18 隔直型拓扑带载120°移相输入电流波形图

图19 硬件实物图

4 实验验证

图19为隔直型拓扑无线电能传输系统实物图,输入直流电压由外部电源供电,电感值为7 μH,接收端补偿电容为47 nF,在实验测试中固定系统的工作频率为206 kHz．

分别对搭建的传统并联谐振电路和隔直型拓扑无线电能传输电路进行实验验证.如图20是开关管驱动波形图,图21、图22为拓扑软开关波形,两种拓扑电路均实现了零电压启动,且隔直型拓扑电路驱动波形和开关管电压应力波形更加平滑.图23为在空载情况下测得两种电路单路的静态输入电流波形is,图24为三路移相空载情况下输入电流波形,图25是空载下电感电流波形,从图中可以看出,传统拓扑输入电流波形畸变较为严重且移相后电流峰值没有发生变化,其中隔直型拓扑单相输入电流更加平滑,类似于正弦波且三路移相后有效减少了电流纹波．

图26为两种拓扑单相带载输入电流波形,图27为传统拓扑三路移相带载输入电流波形,图28是隔直型拓扑三路带载输入电流波形.由图26可知,隔直型拓扑带载后波形没有明显失真,传统拓扑带载后输入电流波形明显失真,说明隔直型拓扑带载能力更强.从图24和图28看出隔直型拓扑三路移相带载后波形没有失真依旧平滑,而图24和图27得到的传统拓扑三路移相带载后波形突变更严重.综上所述,隔直型拓扑引入负载后波形依旧平滑没有震荡,但是传统拓扑输入电流波形震荡明显．

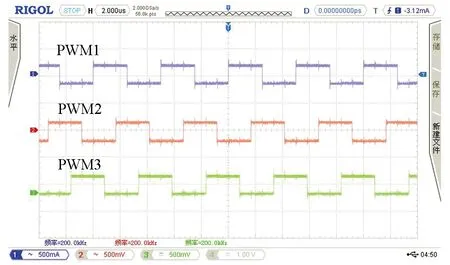
图20 驱动波形图

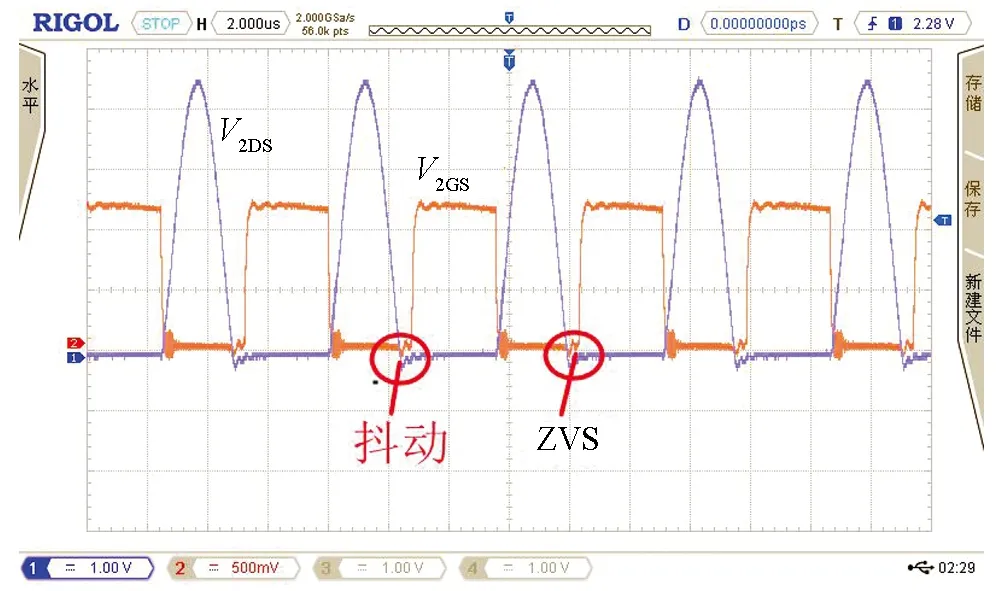
图21 传统型拓扑软开关波形

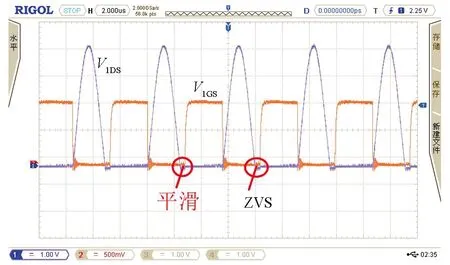
图22 隔直型拓扑软开关波形

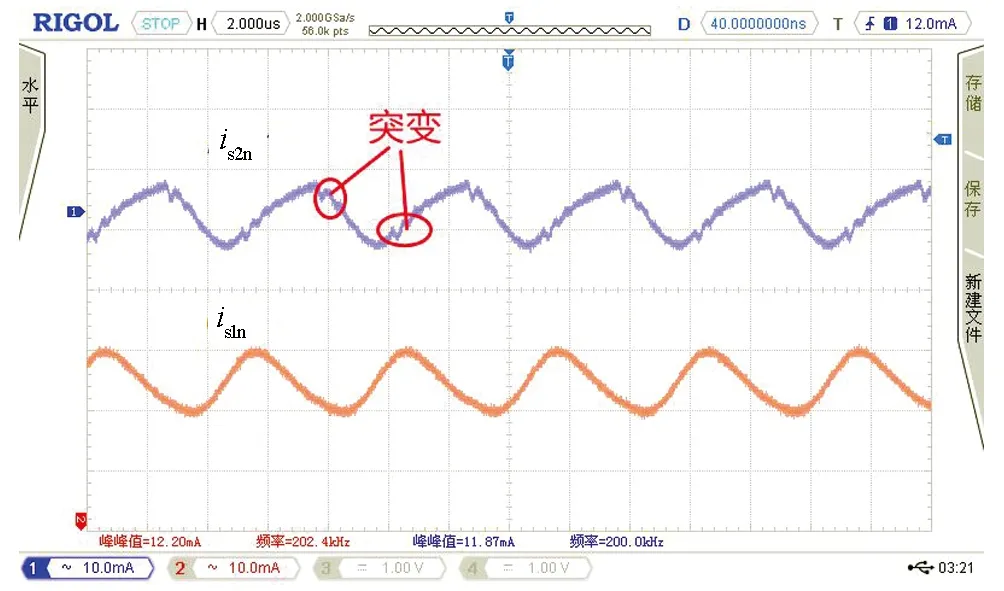
图23 两种拓扑静态输入电流波形

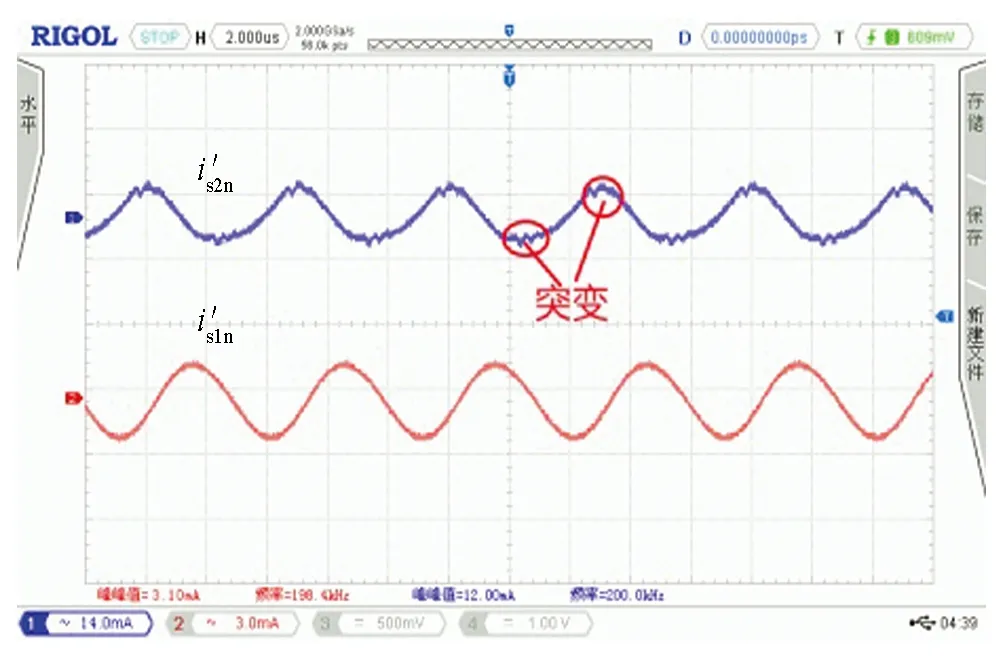
图24 三路移相空载情况下输入电流波形

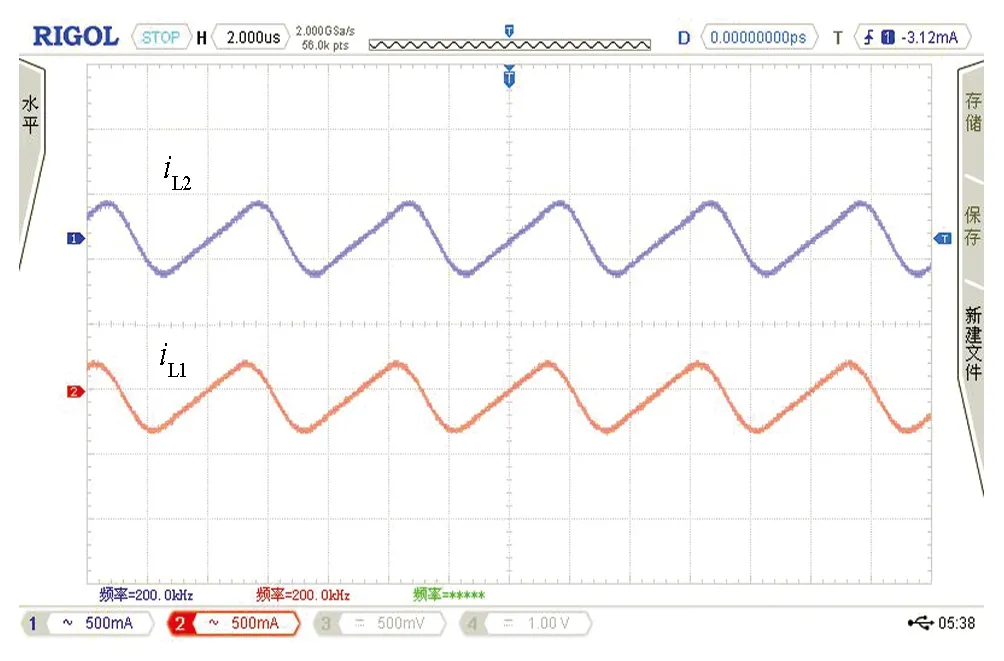
图25 空载下电感电流波形

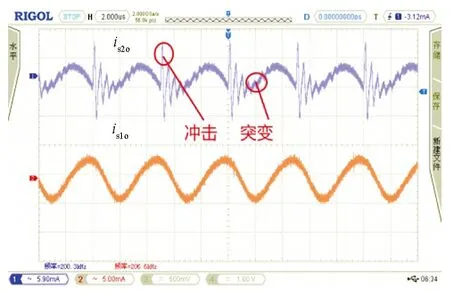
图26 两种拓扑单相带载输入电流波形

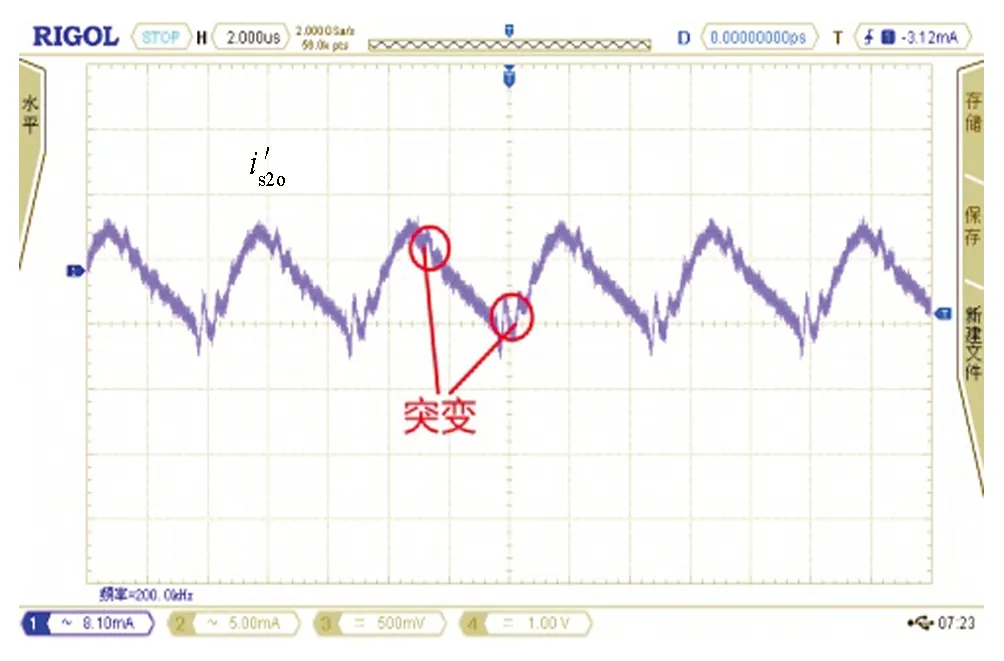
图27 传统型拓扑三路移相带载输入电流波形

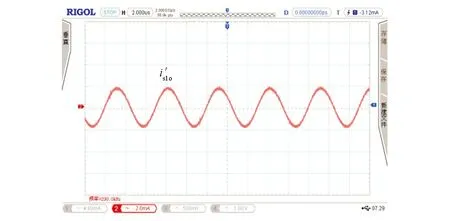
图28 隔直型拓扑三路移相带载条件下120°移相输入电流波形

将实验数据进行归纳整理得出两种拓扑输出功率对比图(图29，图30).从图可知,在输入电压为12 V、负载为10 Ω时,两种拓扑的输出功率范围都在20～28 W.图30为两种拓扑在输入电压为12 V,负载为10 Ω条件下,不同输出功率时传输效率对比图,由图可知,隔直型拓扑电路最大效率可达82%,传统型拓扑电路最大效率为81%,隔直型拓扑电路整体传输效率均高于传统型拓扑电路,从实验的角度验证了理论与仿真的正确性,提高了系统效率,保护了供电电源．

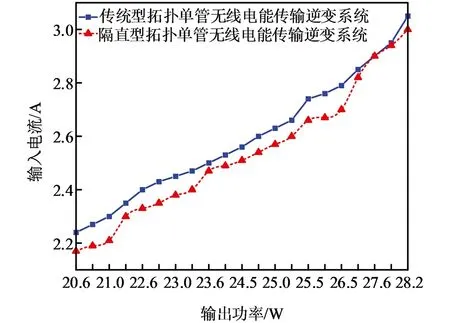
图29 两种拓扑输出功率对比图

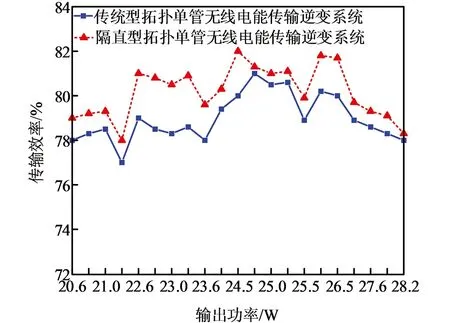
图30 两种拓扑传输效率对比图

5 结论

首先通过模态分析和数学建模得出了隔直型与传统并联两种拓扑下的输入电流模型、电感电流模型和电容的电压电流模型.其次,搭建仿真得出了隔直型拓扑电路对系统输入电流有显著的改善,通过三路120°移相来抑制输入电流纹波,发现隔直型拓扑的纹波抑制能力更强.最后搭建两种拓扑无线电能传输系统平台,在空载和带载下得到两种电路的谐振电感电流、开关管电压和输入电流的实验波形,验证了隔直型拓扑发射端电路能够有效降低系统的静耗,提高充电效率,抑制输入电流纹波的结论．