一种用于周期性事件预测的潮汐模型

■ 景海波 南京信息工程大学

随着我国经济的高速发展，城市空间环境的复杂性急剧上升，各种事故灾害频发，安全风险不断增大，消防救援队伍的任务也越多。新时代的消防业务已经不仅仅局限于火灾的防范和扑灭，在各种灾难或事故现场都有消防队员的出现[1]。消防队员所承担的任务呈现出多样化、复杂化的趋势。

ARIMA 季节性时间序列模型适用于短期预测[2]，是用于单变量时间序列数据预测的最广泛使用方法之一，模型十分简单，只需要内生变量而不需要借助其他外生变量。

多项式回归的最大优点就是可以通过增加x 的高次项对实测点进行逼近，直至满意为止。事实上，多项式回归可以处理相当一类非线性问题，它在回归分析中占有重要的地位，因为任一函数都可以分段用多项式来逼近。但是当x 的次数越高时，拟合出来的方程就越复杂，可能导致往后预测的结果产生较大的误差。

一、模型建立与求解

（一）ARIMA 季节性时间序列模型

把数据看作时间序列，用Box-Jenkins 方法中的ARIMA（差分整合移动平均自回归模型）模型，对出警次数每月、每年的变化趋势总体进行预测。已知由季节性因素或其他周期因素引起的周期性变化的时间序列，称为季节性时间序列，对应本题即指出警次数按照12个月有季节性变化，符合此种情况，周期s=12。

设本题所给出警次数数据序列Xt， 使用ARIMA(p,d,q) 模型[3]，表示为：

Step1. 计算自相关系数与偏相关系数，检验时间序列的平稳性

如果发现图形有多于1 个不是截尾或拖尾，则说明Xt 不是平稳的，需要做差分运算[4]。

Step2. 进行差分运算，确保原序列变为平稳时间序列；

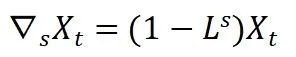
Step3. 进行模型定阶，由差分后的自相关图与偏自相关数据图可知：自相关系数在滞后1 阶后就快速地减为0，偏自相关系数同自相关系数，所以p=1,q=1；

Step4.拟合，估计模型参数；

Step5.用标准化残差进行模型验证。

（二）自新的潮汐模型

首先统计出2016—2020 年5 年内每个月7 类事件发生的次数，并取不同月份各类事件发生的年平均次数，初步判断出第3 类、第7 类事件发生的频率较高且具有一定的周期性。

接着使用最近邻法对7 种事件数据作层次分析，得到事件历年各月的系统树图。根据各类事件的系统树图，以最大标准距离的1/2 作为聚类的判断标准，认为4 类族群以下的事件在发生次数上存在周期性变化，5 类族群以上的事件的发生次数受不同月份，即发生时间的影响较小，呈随机分布。结果表明，周期性变化事件1、3、5、7，非周期性变化事件2、4、6。

为了确保模型建立的可靠性，选择2016—2019 年的数据作为依据样本，2020 年的数据用以检验拟合度，作为模型拟合效果的评价标准。

1.周期性事件1、3、5、7 的四种模型

（1）因为存在周期性变化事件的数据结构相对简单，首先选用多项式回归的方式进行拟合，鉴于当多项式次数达到11 时拟合曲线便与样本曲线完全重合，在1—11 次多项式拟合中遍历搜索拟合程度最优的多项式，发现10 次多项式的拟合程度最优，即与2020 年各月真实值的误差平方和最小，为248。然而实际作出曲线后，显然多项式无法较好地反映出各月次数的变化趋势。

（2）于是我们针对第一类存在周期性特点的事件，建立一个新的反映数据周期性变化的模型。分别取2016 年—2019 年中每年相邻两月的事件发生次数变化率、各月结果的均值作为预测模型中相邻两月的变化率。对于模型中初始值，即一月事件次数，以五年间一月事件次数的最大最小值为上下限，在其中随机取值。

为了寻找此模型对本题数据拟合的最优解，使用遍历搜索方法找出模型的最优初值，使得与2020 年各月真实值的误差平方和最小，其中误差平方和为217，初值为14。得到图像显示拟合的效果仍不够理想。

（3）考虑到前两个模型是基于2016-2019 四年四组数据处理成的一组数据进行分析，必然在经历数据压缩处理后出现部分信息丢失的情况，为了避免这一情况，采用ARIMA 季节性时间序列模型，这既考虑到存在周期性影响因素，又利用2016—2019 年的全部数据对2020年12 个月的事件数据进行了预测。其拟合度相较于前两种模型有较大提升，其误差平方和为132，初值为8，然而这一模型依然存在部分数值与实际数值相差过大的情况。思考后认为这是由于建立ARIMA 模型所依据的数据量仍然太小，部分年份的周期变化中带有的随机干扰（白噪声）被放大了，从而干扰了模型对数据变化周期的计算。

（4）对模型2 进行改进，以2016 年—2019 年4 组数据作相同月份的横向对比，将绝对值大于同月份数据均值的绝对值的数值视为存在较明显的白噪声干扰，为了尽可能减轻影响，最大程度保留数据的变化趋势，将此项数据高过均值的部分保留1/2。

模型改进后的拟合度比ARIMA 模型稍有增高，其误差平方和为127，初值为12。但是由图1 可观察到预测数值与实际数值相差过大的情况显著减少。

图1 四种模型拟合效果对比

结果表示：1 类事件，改进后的周期模型拟合程度最好。

3 类事件，四种模型的误差分别为820、1118、1232×10^4、1118。在拟合时发现2020 年的数据未体现出2017-2019 年间的数据特征，但是与2016 年的数据特征存在相似性，结合3 类事件是季节性事件，推测2016 年与2020 年未体现数据特征的原因在于这两年是存在较强异常气候现象的厄尔尼诺年[5]，导致年内应出现的周期性气候被干扰，灾害增多，救援出警次数的数据特征减弱。

5 类事件，四种模型的误差分别为7、37、19、16。结果表明使用改进的周期模型可以较好拟合数据，但是多项式拟合结果的数值误差平方和要稍小于改进的周期模型，但是无法体现数据的周期性特点。

7 类事件，建立的四种模型对2020 年的拟合效果都不佳，误差分别为290、246、648、382。通过观察发现2020 年数据的变化趋势符合模型拟合出的趋势，但是变化幅度相对较小，认为此事件也受到2020 年厄尔尼诺现象影响，出现数据特征减弱的情况。

2.非周期性事件2、4、6 的两种模型

（1）对于非周期性变化事件2、4、6，首先考虑多项式拟合，由于数据分布的随机性，拟合趋向于一条直线。

（2）考虑非周期性变化事件的随机分布，先以历年数据的最小最大值为下上限，模拟事件次数在此区间的随机分布。再基于2016 年—2019 年数据拟合分布系数，得到此类事件的随机分布模型，在进行多次计算后选取误差平方和小于多项式拟合的一组数据，作为此模型计算2020 年各月份事件次数的结果。

以2016—2019 年四组数据的平均数作为模型的均值，将极小概率出现的过大或过小数值赋以历年数据中的最大或最小值，确保随机分布模型给出的计算数据在合理范围。

结果表示，2 类事件（1）和（2）两模型的误差分别为27、24。4 类事件（1）和（2）两模型的误差分别为137、123。而对于6 类事件，随机分布模型的拟合效果始终无法优于多项式拟合，表明6 类事件也随月份存在周期性变化，则使用周期性模型对数据进行拟合，得到四种模型的误差分别为290、246、648、382。

二、结果分析

根据文献[6],消防出警事件可分为火情，抢险救援，社会救助。

对于数量接近一半的7 号事件，考虑到其具有周期性且于2 月( 春节烟花爆竹) 与6 月( 夏季炎热干燥)出现高峰，推测此事件为火情。2、4 为随机发生的无周期事件，则认为其为开门取钥匙，救助猫狗这类的社会救助类。其余1、3、5、6 类事件可定性为抢险救援，其中5 类事件由于其显著的周期性特征，即事件发生集中于5—8 月，因此可推测是抗洪抢险事件。

三、模型推广

本文以某地为例，分析了各类火警救援事件与时间的关系，从事件是否有周期性角度出发，对不同类型救援事件次数与时间进行了拟合预测，验证了自新的潮汐模型应用于周期性事件拟合预测和消防救援出警次数统计分析是可行的。以上研究能够帮助消防队对其救援的事件有更深入的了解，提前做好培训工作并制定更加有效的应对方案，还对政府实施社区宣传预防措施有一定的参考价值。