基于线模量波速时间差的10 kV自闭/贯通线路故障测量

刘秦娥，王晓东

（国网湖北省电力有限公司襄阳供电公司，湖北 襄阳 441100）

0 引 言

铁路10 kV自闭/贯通线，在铁路电气系统中具有重要的作用。但因为线路附近常有各种施工现场，复杂环境等因素，经常造成线路故障，且造成的故障类型多变复杂，想要定位故障也较为困难[1-3]。

目前，传统的故障测距方法主要有2种，即阻抗法和行波法。但上述的2种方法在10 kV自闭/贯通线路不再适用。因为该线路的在平常状态下是单个电源供电，且由架空线路和电缆线路2种线路混合线路构成的。故障点产生的故障行波含有2种分量，一种是线模分量，另一种是零模分量。区分这2种分量的重要因素之一是这2个行波分量的波速不同[4-7]。因而本文针对该特点将其按照线路段上不同的波阻抗进行分段。由此根据行波到达同一端的时间差值作为故障测距的关键变量，从而便可以计算出故障距离。

1 混合线路模量波速法故障测距

电缆-架空线混合线路模型如图1所示，其中M、N为线路2端，将线路平均分成n份，分别为x1,x2,…,xn。

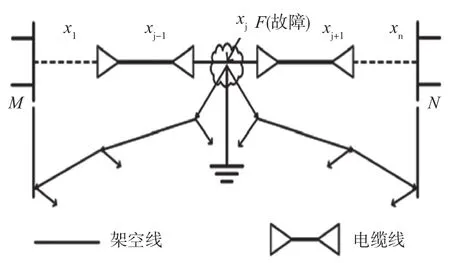
图1 电缆-架空线混合线路模型

由图1可知，xjF表示在t0时刻，线路j发生单相接地短路故障（其中F为发生故障的位置），则由相关模分量的计算公式为

式中：t1为线模分量到达端线的时间；t0则为零模分量；第i段线路中线模波速和零模波速分别为相应的计算结果为

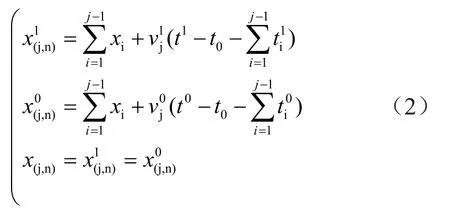
当j=1时，作下述等式变换

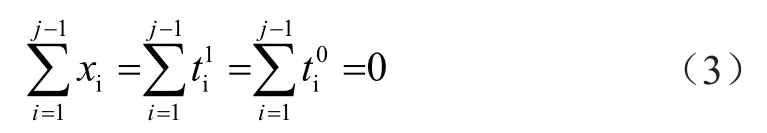
同时，化简式（2）可得

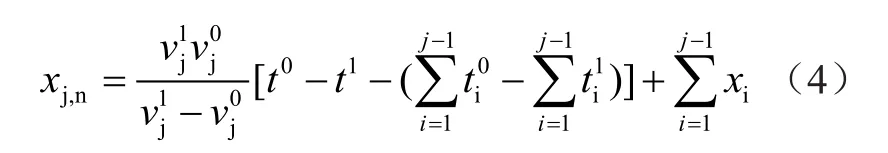
若令

则式（4）则可化简为

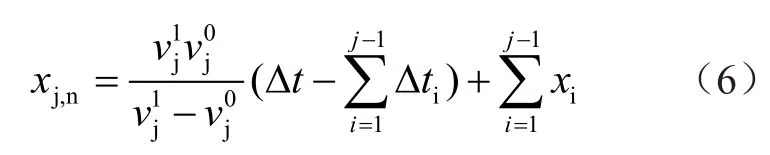
由式（6）可得

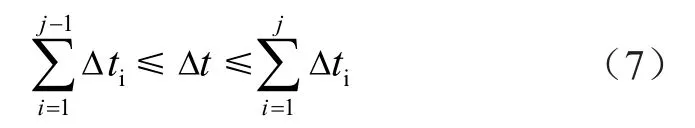
则上式即为故障距离计算的判别式。

2 故障定位的具体实现方法

2.1 模量分量的波形获取

通过解耦的方法获得模量分量的波形。如图2所示为3个横模分量行波的演示图。空间模量是前2个分量，其传播的方法是以输电线路为1个回路；地中模量则是以大地为分量。

2.2 两个模分量的波速计算

在分布参数电路中，通过求解电磁波波动方程即可确定波速，公式为

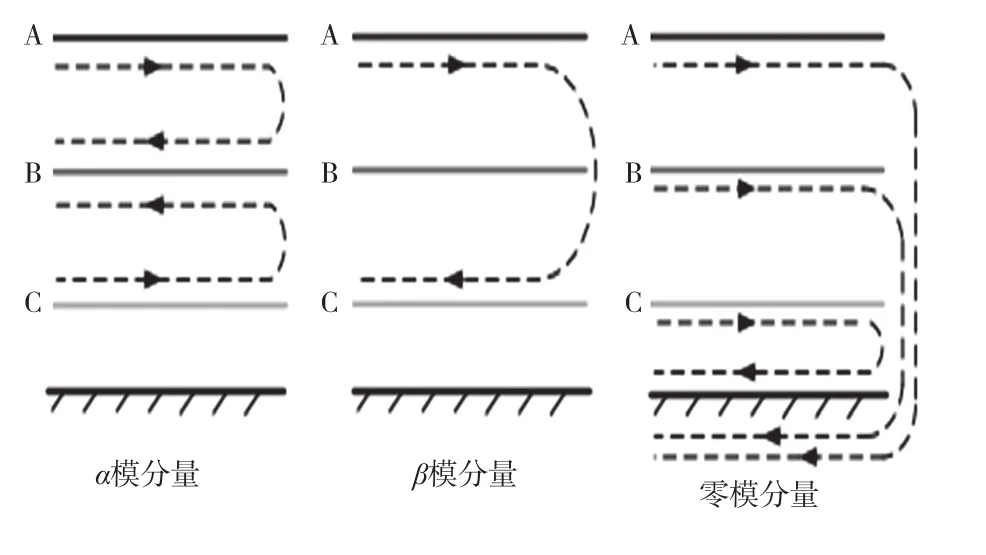
图2 三相输电线路的α、β、零模分量

式中：vq为行波波速；w为角频率；βq为衰减常数。衰减常数计算公式为

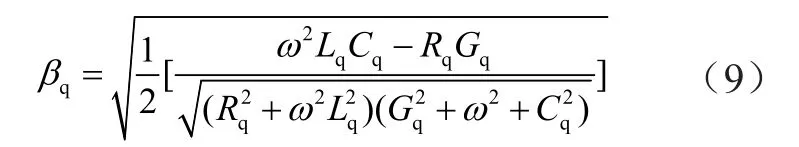
式中：Rq、Lq、Cq和Gq分别为均匀有损输电线单位长度正序、负序或零序的电阻、电感、电容和电导。

当系统正常运行时的波形是平稳的，而一旦发生故障，则波形会出现突变，出现1个非平稳信号，由波形出现的突变点来确定行波的波头位置[8]。

本文使用小波变换的波形变换算法来识别波形发生突变，如图3所示为小波变换时域图。

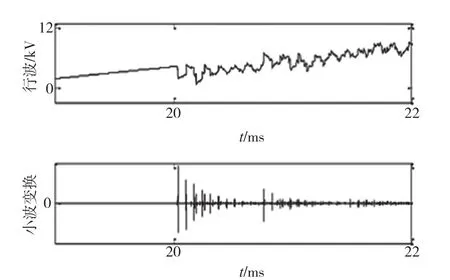
图3 故障行波及其小波变换时域图

可以由上述算法快速检测到波头。

3 仿真分析

为了验证本文提出算法的有效性，通过MTLAB的仿真模块来进行验证。首先建立1个10 kV自闭/贯通的线路，为了保证架空线路和电缆线路的混合，本文使用电缆和架空线路交替的模型，一共6段混合线路。本文设线路总长度为60 km,则每段混个线路的长度为10 km。根据式（6）和判别式（7），得到如图4所示的曲线。

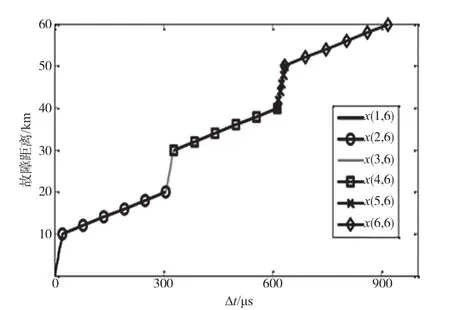
图4 仿真模型故障距离与模量行波时间差特性曲线

在仿真中，设置仿真时长为0.04 s,采样的频率为2 MHz,则得到的线路首端分量行波如图5、图6所示。

图5 线模故障电压行波

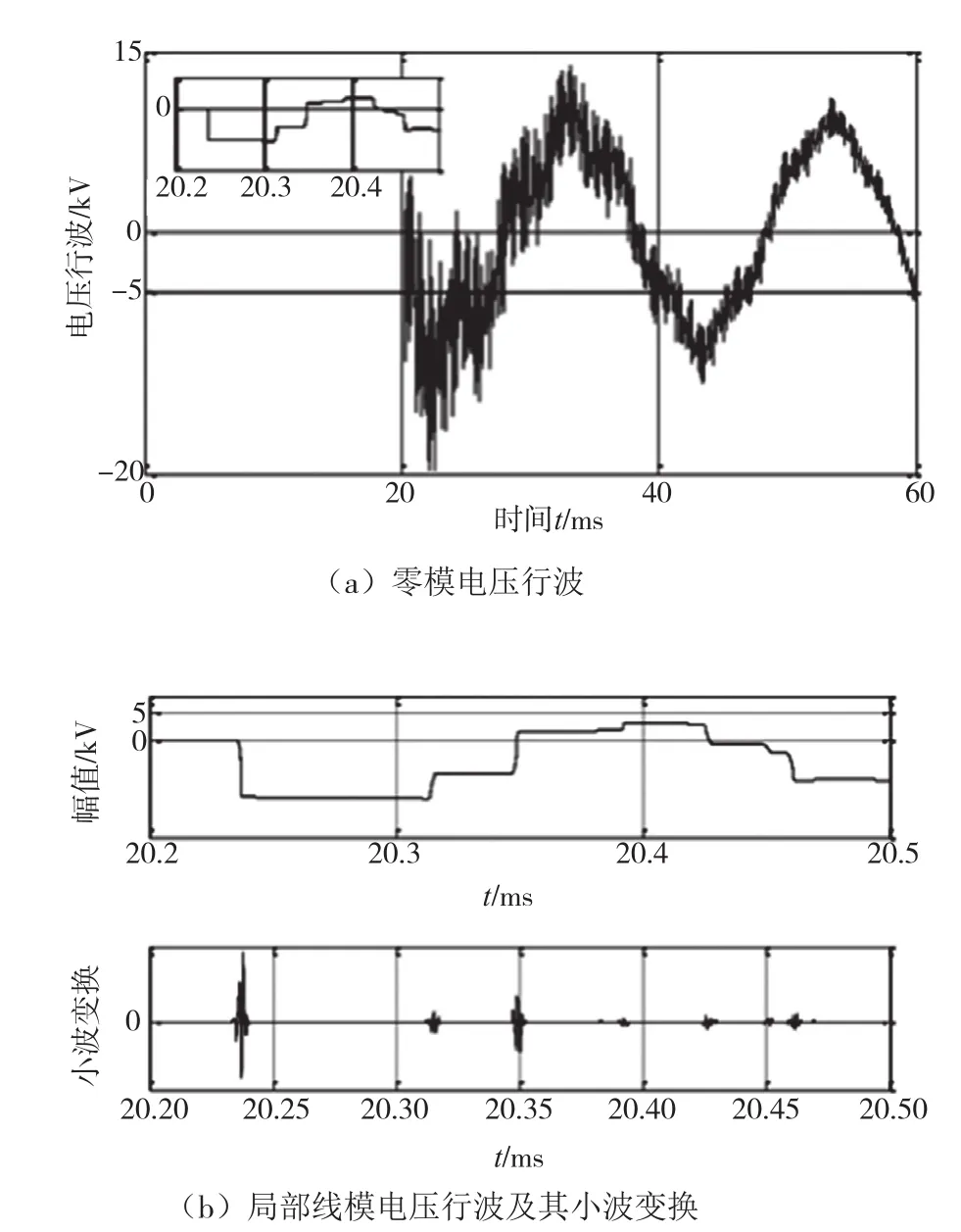
图6 零模故障电压行波

则由上述可以计算出故障距离为

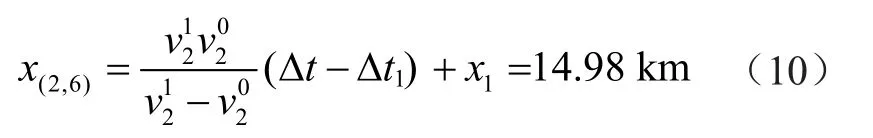
在线路其他的故障位置获得的情况如表1所示。

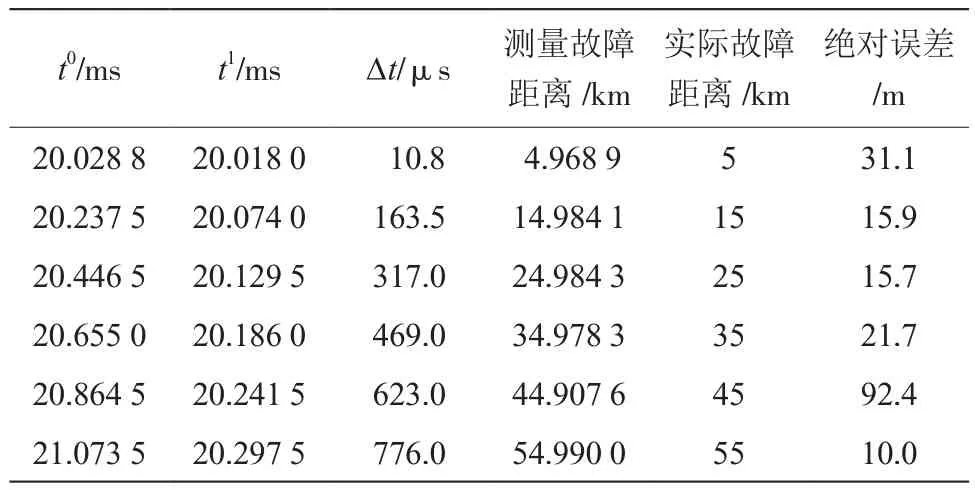
表1 模量行波时间差值法故障测距结果

上述的结果表明，本文提及的算法具有较高的鲁棒性和精度。

4 结 论

针对传统行波算法不适用于多段的混合线路这一现状，提出一种弥补该缺陷的改进算法。首先，利用2种模量不同的波速来弥补传统算法中需要精确的时钟同步的这一缺点。其次，在不同的故障点进行比较，确定算法的鲁棒性。最后，利用MATLAB的仿真模块进行对上述方法的验证，结果表明了本文提出的方法的有效性。