基于LM-GAUSS固体火箭发动机羽流光场测温方法

李金键，王丙寅，齐 琪，张 彪，许传龙

(东南大学 大型发电装备安全运行与智能测控国家工程研究中心&能源与环境学院，江苏 南京 210096)

引 言

固体火箭发动机的燃烧产物经喷管加速后喷出的火焰流简称为固发羽流。固发羽流具有温度高、流速快、强辐射等特性[1-2]。羽流温度的准确测量能够为发动机流场仿真和燃料特性研究等提供重要依据，并指导工程热防护实践[3-4]。目前，接触式测温方法受限于探针材料的性能，难以满足羽流测温范围需求。基于光场相机的非接触测温方法，凭借测温范围宽、响应快、可靠性高等优点被广泛应用于火焰温度测量[6-8]。该方法基本思路是利用火焰自发辐射的光谱信息构建关于温度与物性参数的方程组，通过求解该方程组，进而获得火焰温度分布。这类问题属于辐射传输反问题范畴，其主要难点是极小的测量噪声可能会导致极大的求解误差[9]。因此，选择有效的重建算法至关重要。

目前，对于辐射传输反问题的求解算法主要分为以下3类：第一类是正则化算法，例如吉洪诺夫正则化算法、截断奇异值分解算法(TSVD)[10]、最小二乘QR分解算法(LSQR)[11]、非负最小二乘算法(NNLS)等。正则化算法由于需要选取合适的正则化策略和预估辐射特性参数，难以适用于羽流三维温度分布重建；第二类算法为智能优化算法，例如模拟退火算法(SA)[12]和代数迭代算法(SART)、微粒群算法[13]等。智能优化算法随着重建网格划分数量的增加，重建时间急剧增加，难以满足快速、高分辨的三维温度分布重建的需求[14]；第三类算法为混合算法，该类算法是将不同算法各自的优势有机结合，实现算法间的优劣互补，从而提高算法整体性能。例如NNLS-LMBC混合算法[15]、LSQR-CG算法[16]等。当前混合算法的研究中普遍存在重建精度较低、鲁棒性差等问题。因此，有必要构建一种鲁棒性强、求解精度高的重建算法。

Levenberg-Marquaredt(LM)算法是非线性优化算法的一种，其具备优秀的全局搜寻能力，能够快速地接近最优解，因此被广泛应用于非线性问题的求解[17]。Gauss-Newton(GAUSS)算法具备优秀的局部搜寻能力和较快的收敛速度[18]。两种算法的结合能够较好地解决现有三维温度求解算法重建精度低、鲁棒性差等问题。

因此，本研究建立了基于单光场相机的羽流辐射传输模型，并提出了一种基于LM-GAUSS混合算法的羽流三维温度重建方法。通过在循环迭代过程中，对辐射特性参数进行调整，进而减弱求解问题病态性对求解过程的影响。通过数值仿真和实验研究，在一定程度噪声的条件下，对比分析了LSQR、NNLS算法与所提混合算法的重建性能，为重建固发羽流温度分布提供高可靠性、高精度的重建算法。

1 基于光场成像的羽流测温模型

该模型主要由光场相机、待测物体两部组成，如图1所示。光场相机由主透镜、微透镜阵列与传感器3部分组成，羽流自发辐射光线通过光场成像系统后被传感器接收，由于背景辐射强度相较于羽流辐射强度可以忽略，通过单次曝光即可获得羽流自发辐射的光线位置、方向与强度等信息。将采集的光谱辐射信息与重建算法相结合，即可实现羽流三维温度分布的重建[7, 8]。

羽流内部的辐射传输过程由辐射传输方程进行描述，方程如下所示：

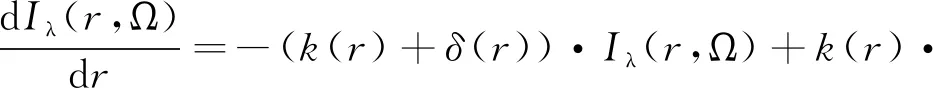
(1)

式中：Iλ(r,Ω)为r位置处波长为λ并沿Ω方向传输的光谱辐射强度，W/(m3·sr)；k(r)为吸收系数，单位为m-1；δ(r)为散射系数，m-1；Ф(Ω′,Ω)为羽流在r位置处的散射相函数；Ibλ(r)为黑体辐射强度，W/(m3·sr)。

为简化研究过程，仅考虑其吸收特性[19-20]。结合光学厚度定义，如式(2)所示，将由上述方程推导得到相邻网格间的辐射传输方程，如式(3)所示。

Δτ=kΔL

(2)

Iλ(r+Δr,Ω)=Iλ(r,Ω)·exp[-k(r)·ΔL]+

Ibλ(r)·(1-exp[-k(r)·ΔL])

(3)

式中：Δτ为光线沿Ω方向穿过网格的光学厚度，无量纲；ΔL为光线沿Ω方向穿过网格的距离，m；Δr为沿Ω入射方向上相邻网格的距离，m。

若将羽流划分为V个网格，并按一定排列方式将各网格编号(1，2，v，…，V)，光场相机图像探测器共M个像素接收到辐射光线，并按一定排列方式将各像素编号(1，2，m，…，M)。对于任意一个像素m的辐射光线，其穿过的羽流网格总数记为n，则辐射光线方向将各网格编号依次记为v1，v2，vi，(vj)，…，vn，结合式(3)可得到各像素辐射光线的光谱辐射强度，如式(4)与式(5)所示，将N条光线计算式联立可得离散的辐射传输方程组，如式(6)所示。温度可通过求解方程组后，由黑体辐射定律获得，如式(7)所示。

(4)

(5)

(6)

A·Ibλ=Iλ,ccd

(7)

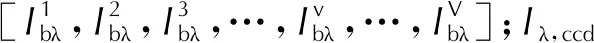
2 LM-GAUSS算法

LM-GAUSS混合算法的基本原理是在循环迭代过程中，通过比较当前目标函数与梯度向量的无穷范数来选择该次迭代需使用的算法，并使用所选择的算法计算求解向量该次迭代需前进的步长，直到目标函数满足终止条件或满足最大迭代次数为止[21]。两种算法的结合能够保证求解精度的同时，提高了算法鲁棒性。

结合羽流温度重建问题，目标函数向量f和目标函数F的定义如式(8)、式(9)所示，求解过程中算法的选择策略如式(10)所示：

f(x)=A·Ibλ-Iλccd

(8)

(9)

(10)

式中：J为雅可比矩阵；hGAUSS为GAUSS算法计算的前进步长；hLM为LM算法计算的前进步长；F′(x)为目标函数的梯度向量；B为GAUSS算法的系数矩阵；μ为LM算法的阻尼系数；I为单位矩阵。LM-GAUSS混合算法步骤与流程图如下：

图2 LM-GAUSS算法流程图Fig.2 Flow chart of LM-Gauss algorithm

步骤一：对温度T随机赋值，将吸收系数k与温度T组成初始迭代向量x，设定最大迭代次数itermax与算法截止值ε1，ε2。

步骤二：设定初始迭代的算法类型Method=LM；迭代状态数Better=false；满足选择GAUSS算法条件的次数计数器值count=0；对LM算法中阻尼系数的调整因子q=2；GAUSS算法初始系数矩阵B=I；迭代次数计数器值iter=0；GAUSS算法中解向量x前进步长调整因子Δ=0。

步骤三：计算当前目标函数F、雅可比矩阵J、函数向量f、混合算法终止条件数Found与LM算法的阻尼因子μ。其中，阻尼因子取转置雅克矩阵与其自身相乘后矩阵对角线元素的最大值，如式(11)与式(12)所示。

Found=‖F′(x)‖∞≤ε1

(11)

u=max{diag(JTJ)}

(12)

步骤四：判断Method是否为LM，若是则继续下一步骤，否则转到步骤六。

步骤五：将相关参数Found、x、count、μ、q、J、f输入LM算法模块进行计算，返回参数xnew、Found、Better、Method、count、μ、q、Δ后转到步骤七。

步骤六：将相关参数Found、x、B、Δ输入GAUSS算法模块进行计算并返回获得的参数(xnew、Found、Better、Method、count、Δ)。

步骤七：根据BFGS策略对系数矩阵B进行更新。

步骤八：判断状态数Better是否为true。若是，则更新当前解向量x=xnew；

步骤九：判断混合算法条件数是否为真或iter>itermax。若混合算法条件数为1，则将当前解向量并转化为温度重建值T，继续下一步骤，否则iter=iter+1，转到步骤三。

步骤十：输出重建温度值T，结束计算。

3 仿真计算结果与讨论

通过仿真计算对混合算法性能进行研究，将半径Rmax为8mm，高度Hmax为30mm的圆柱羽流沿轴向、径向和周向进行划分，如图3所示。同时，选取610nm和530nm为中心波段的两组光谱辐射信息构建离散化的辐射传输方程组，设定羽流温度T(K)与吸收系数k(m-1)的分布函数，如式(13)、式(14)所示，图3中AD为轴向方向，RD为半径方向，CD为周向方向。

(13)

(14)

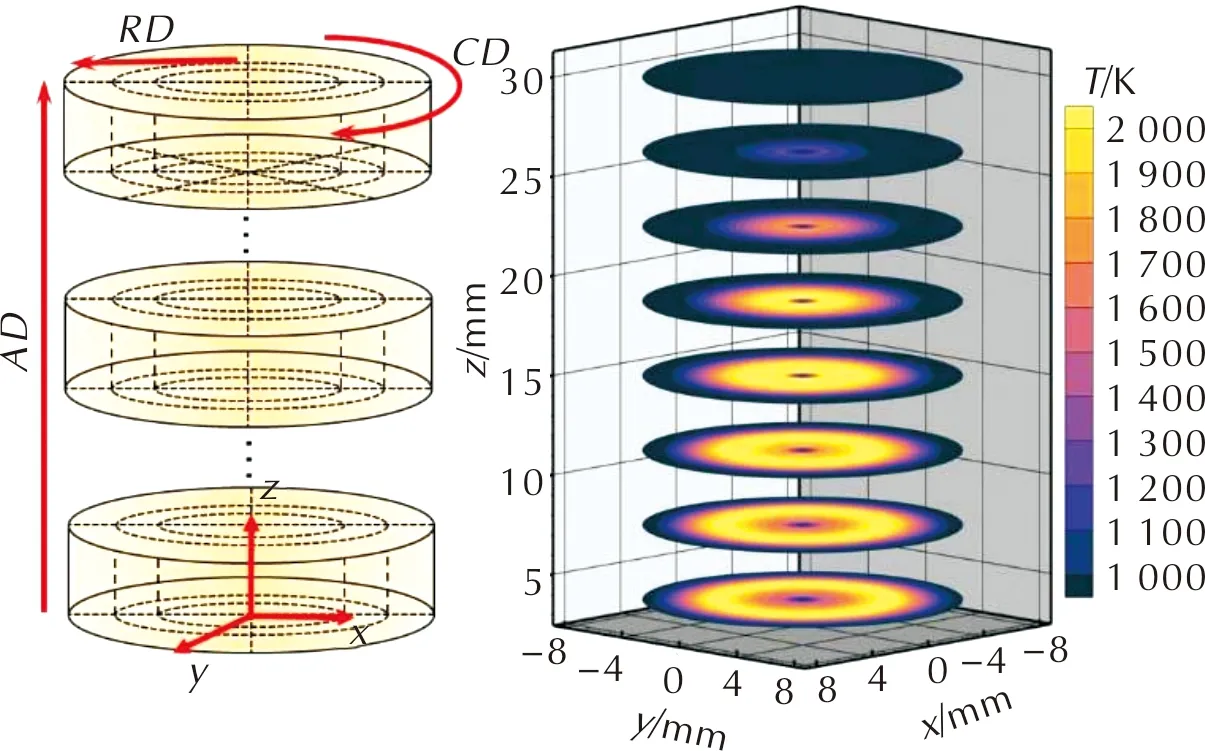
图3 网格划分与设定温度分布图Fig.3 Grid partition and setting temperature distribution

为研究噪声对算法性能的影响，在添加2%至10%不同程度的高斯白噪声后，使用混合算法对三维温度进行重建，并通过比较平均重建误差对算法的准确性与鲁棒性进行评估，噪声添加公式与平均重建误差的定义如式(15)～式(17)所示：

(15)

(16)

(17)

式中：In,ccd为第n根光线的辐射强度，W/(m3·sr)；In,ccd,exact为第n根光线准确的辐射强度值；noiseI为对辐射强度的高斯白噪声强度，无量纲；km为第m个网格的吸收系数；km,exact为网格准确的吸收系数值；noisek为对吸收系数的高斯白噪声强度；ζ为均值为0，标准差为1的正态分布随机数；δT为温度平均重建误差。

3.1 辐射强度噪声下算法性能对比

对辐射强度添加不同程度的噪声后，使用LSQR、NNLS与LM-GAUSS这3种算法对温度进行重建，结果如图4示。

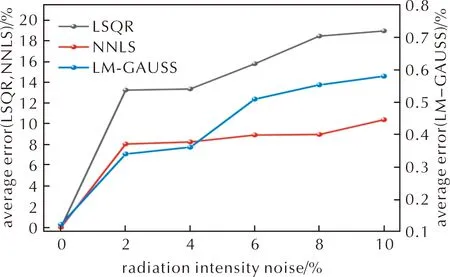
图4 辐射强度噪声下算法重建误差图Fig.4 Reconstruction error under radiation intensity noise

由图4可知，3种算法均能在无噪声条件下准确地重建羽流三维温度分布。随着辐射强度噪声增加，由于LSQR算法在求解过程中无法保证温度非负性的特征，因此，算法的平均重建误差高于NNLS算法。当辐射强度噪声大于2%时，LSQR算法的平均重建误差高于10%，NNLS算法的平均重建误差高于7%。其主要原因是待求解问题属于病态问题，系数矩阵过大的条件数导致在求解过程中极小的强度噪声会造成极大的重建误差。

随着强度噪声的增加，LM-GAUSS算法重建误差略微增加，最大平均重建误差为0.6%。其证明了在含有辐射强度噪声重建时，LM-GAUSS算法具有比LSQR、NNLS算法更高的重建精度与更强的鲁棒性。

3.2 吸收系数噪声下算法性能对比

在求解离散化的辐射传输方程时，吸收系数会含有一定程度的噪声。为讨论该部分噪声对算法性能的影响，使用LSQR、NNLS以及LM-GAUSS算法在添加吸收系数噪声的条件下对羽流三维温度进行重建，结果如图5所示。

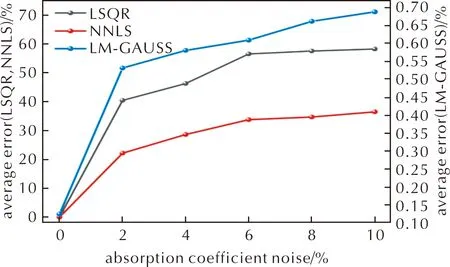
图5 吸收系数噪声下算法重建误差图Fig.5 Reconstruction error under absorption coefficient noise

随着吸收系数噪声增加，LSQR算法的重建误差快速增加至40%以上，NNLS算法的重建误差快速增加到20%以上。主要原因是对吸收系数添加噪声后，系数矩阵产生了较大偏差，加剧了问题的病态程度，使得重建误差远大添加辐射强度噪声时的重建误差，此时上述两种算法已经无法在含有吸收系数噪声的条件下对温度进行求解。

LM-GAUSS算法在计算过程中，对含有噪声的吸收系数进行调整，能够减弱吸收系数噪声对问题求解的影响。随着吸收系数噪声的增加，算法重建误差略微增加，最大平均重建误差为0.7%。上述结果表明，相比于LSQR、NNLS算法对吸收系数噪声过于敏感的问题，LM-GAUSS算法具有更好的重建性能，证明了LM-GAUSS算法是优于NNLS、LSQR算法的选择。

3.3 不同噪声水平对LM-GAUSS算法的影响

在实际过程中，吸收系数噪声与辐射强度噪声同时存在，因此，设立以下4种工况，如表1所示，使用LM-GAUSS算法对温度进行重建，重建后的温度分布如图6所示。

表1 数值计算的工况设计表 Table 1 Working condition design example

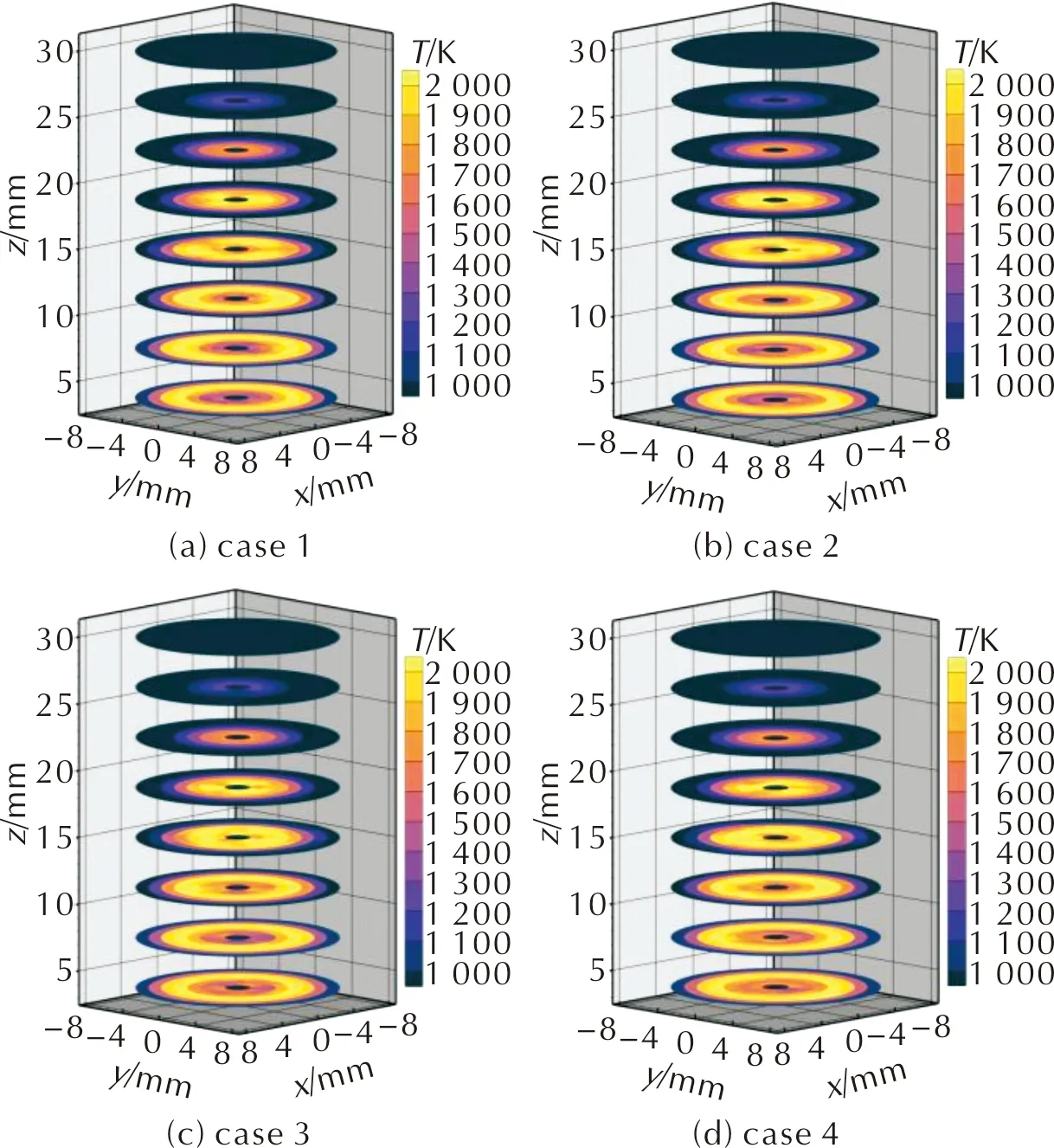
图6 不同噪声条件下温度重建分布图Fig.6 Temperature distribution under different noise conditions

在不同的噪声条件下，LM-GAUSS算法均能够较准确地重建羽流内部的温度分布，4种工况对应的平均重建误差分别为1.67%、2.1%、2.58%和4.66%。随着噪声的增加，靠近中轴线位置的重建误差增加，但温度分布与设定趋势保持一致。羽流头部的温度与设定温度相比偏高，可能与穿过头部网格的光线数量较少有关。在吸收系数噪声与辐射强度噪声条件同时存在时，混合算法的重建误差优于5%，保持在可接受范围内。

3.4 网格数量对LM-GAUSS算法性能影响

在三维温度测量过程中，网格划分数量越多，分辨率越高。因此，需要讨论网格数量对LM-GAUSS算法重建性能的影响。本研究设计了3种不同的网格划分形式，如表2所示，在分别含有吸收系数噪声与辐射强度噪声的条件下对温度进行重建，重建结果如图7所示。

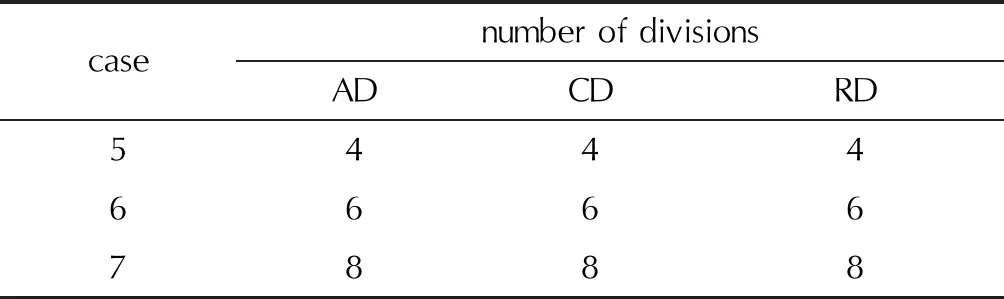
表2 网格划分工况设计表 Table 2 Design of grid number example

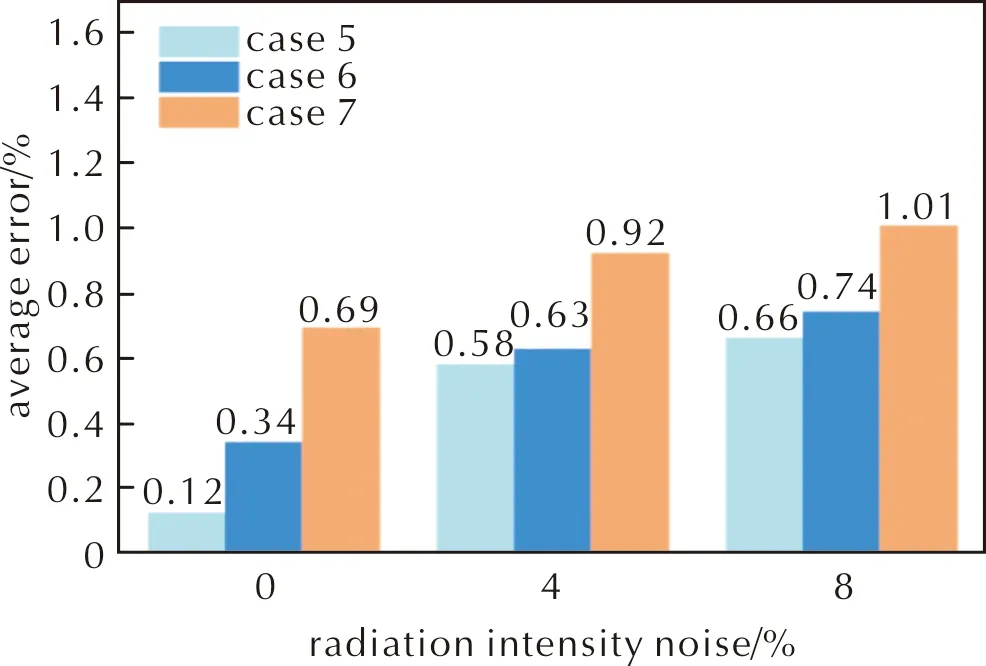
图7 辐射强度噪声下网格数量对重建误差的影响Fig.7 Influence of mesh number on the reconstruction error under radiation noise

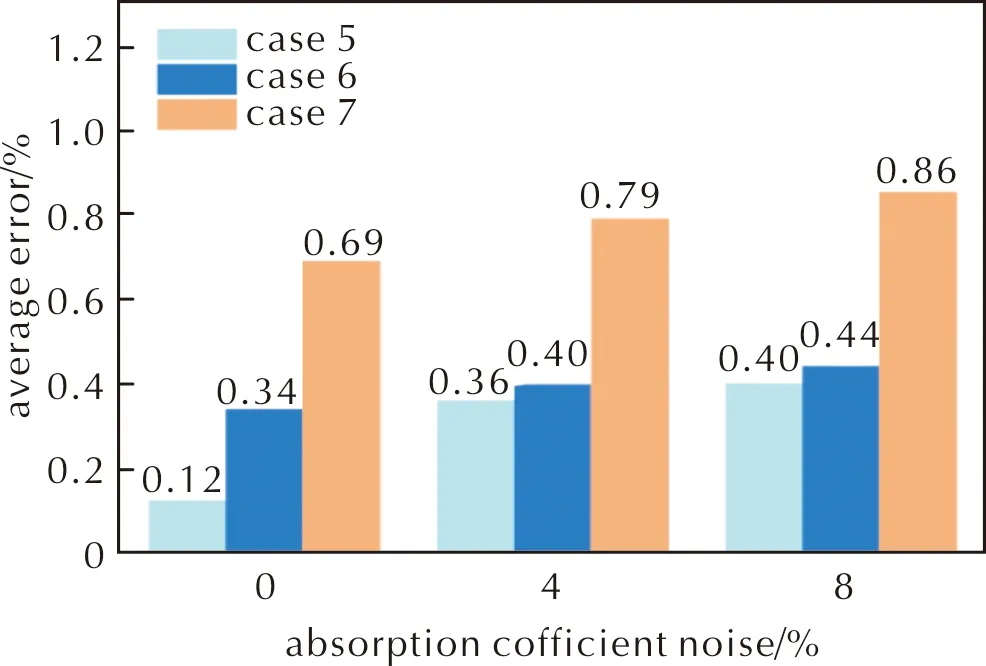
图8 吸收系数噪声下网格数量对重建误差的影响Fig.8 Influence of mesh number on the reconstruction error under absorption coefficient noise

由图7与图8可知，在噪声不变的条件下，随着网格数量增加，平均重建误差略微增加。其主要原因是网格数量越多，对应解向量的维度越大，问题的病态性越强。对比两种情况可发现LM-GAUSS算法在网格数量增加过程中，对辐射强度噪声更为敏感，其重建误差增加程度更大。当网格划分较多时，辐射强度噪声下混合算法的重建误差低于3%，吸收系数噪声下的重建误差低于1.5%，证明了LM-GAUSS算法能够在高分辨率条件下重建三维温度分布。

综上所述，通过比较不同噪声条件下传统LSQR、NNLS算法与LM-GAUSS算法的性能，验证了LM-GAUSS算法具备更高的重建精度以及更强的鲁棒性，并讨论了网格数量对LM-GAUSS算法性能的影响，结果表明，随着网格数量的增加，重建误差略有增加，但仍保持较高的重建精度，可为后续固体火箭发动机热试车试验提供算法依据。

4 试验结果与分析

为了进一步研究算法在重建实际火焰的性能，基于课题组的燃烧平台，对乙烯层流扩散火焰进行温度重建，实验装置如图9所示。

图9 乙烯扩散火焰拍摄装置Fig.9 Ethylene diffusion flame temperature measurement device

燃烧工况参数如下，乙烯流率VC2H4为0.08L/min，空气流率VO2为3L/min。光场相机由主镜头(Nikon NIKKOR 50mm f/1.8D)、微透镜阵列(F数为4.2，透镜单元尺寸为100μm×100μm)、相机(分辨率为3312×2488，像素大小为5μm)组成。使用光场相机对火焰进行拍摄，通过光场相机拍摄到的光场图像，如图10(a)所示。再利用黑体炉进行辐射强度标定，获得光线的辐射强度分布，将火焰区域划分8×8×8的网格，重建得到温度分布，如图10(b)所示。将热电偶(型号为Omega P13R-020)测量火焰中心位置的温度作为参考点，验证算法重建精度。

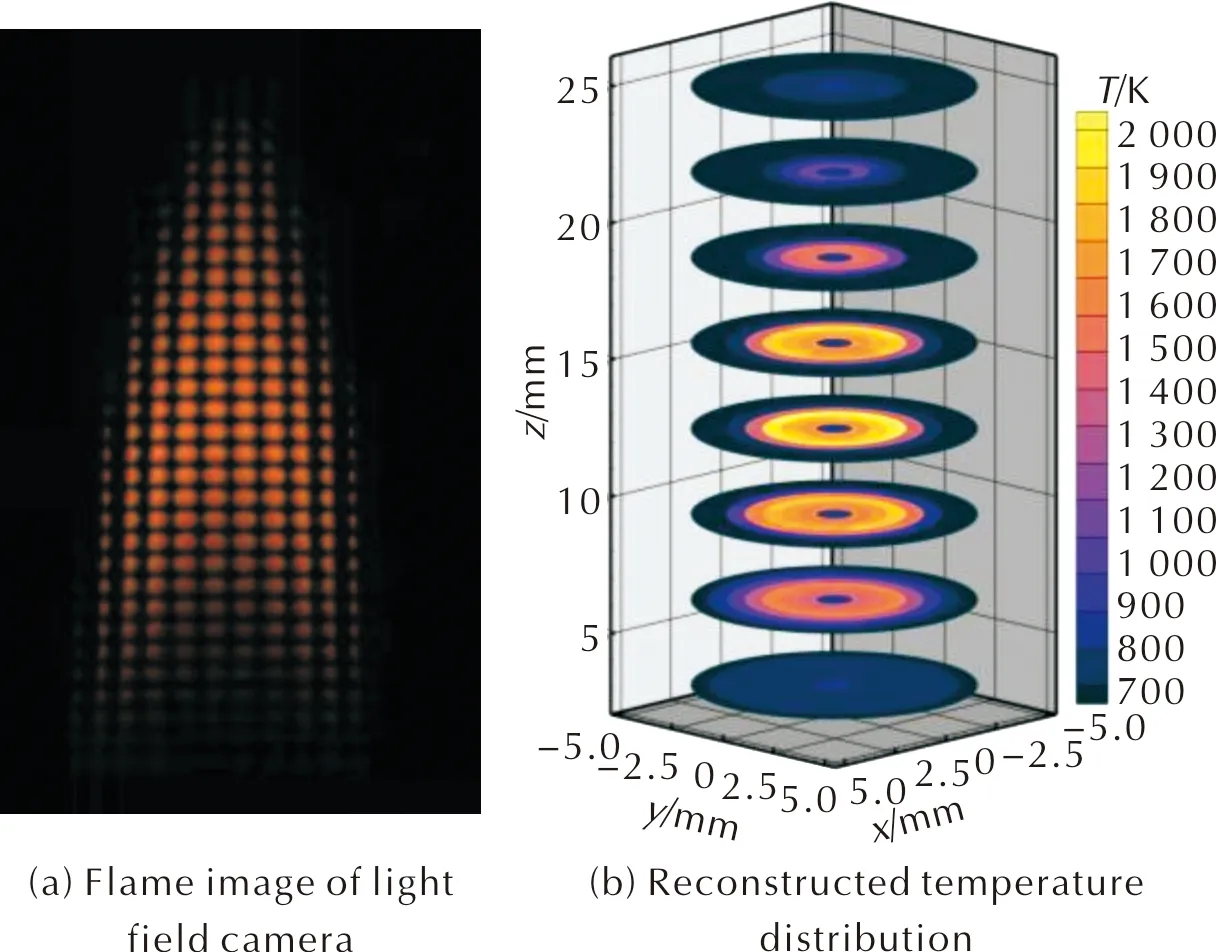
图10 光场相机的火焰图像和重建温度分布图Fig.10 Flame image of light field camera and reconstructed temperature distribution

由图10(b)可知，重建火焰温度范围在700～2200K范围内。火焰中心区域算法重建温度为1431K，热电偶测温为1350K，相对误差为6%。火焰的重建最高温度为2214K，最低温度为700K。随着高度的增加，火焰高温区域的半径逐渐减小，符合实际火焰温度分布的特点，证明LM-GAUSS算法能够较好地反应实际火焰的三维温度分布特点，验证了其重建实际火焰的可行性。

5 结 论

(1)对比LSQR、NNLS与LM-GAUSS算法的重建结果，验证了LM-GAUSS混合算法重建精度高、鲁棒性强的特点。分析了网格数量对算法重建精度的影响，结果显示随着网格数量的增加，重建误差略有上升，但仍优于5%。

(2)使用LM-GAUSS算法对乙烯扩散火焰的温度场进行重建试验，证明了算法在重建实际火焰的可行性，为后续开展固体火箭发动机温度场现场测量提供了算法支撑。