小波去噪及PSO-BP神经网络模型在地铁沉降监测中的应用

常旭辉

(中国电建集团北京勘测设计研究院有限公司 北京 100024)

0 引言

城市轨道交通作为一座城市重要的交通工具,涉及每个市民的切身利益。轨道交通为市民带来了出行的便利,提升了人民的幸福感与获得感。与此同时，各大城市正在建设地铁项目,促进当地经济的发展。在地铁建设过程中能够快速准确地获取地表沉降信息,为地铁安全施工提供一种保障是一件意义重大的事情。地铁施工分为明挖法与盾构法,其中盾构法在地铁施工中较常见,在施工中对地表进行监测保障人生与财产安全。研究地表沉降变形机制,制定合理有效的应急措施减少生命财产的损失起到了关键作用。关于地表沉降监测研究,文献[1]中采用相关性分析法,获取各类监测数据并计算关联参数,最后采用多元素拟合回归建立非线性回归模型进行预测,取得了较好的结果。文献[2]中利用小波去噪与时序分析组合方法,建立模型并对比常规模型取得了明显提高。文献[3]中利用灰色模型与长短时记忆神经网络模型,并结合快速非支配遗传算法构建组合模型,得到了较准确的预测结果。组合模型的应用大大克服了传统单一模型预测带来的弊端,为此,本文以某城市地铁一号线为研究对象,收集地表沉降数据。以小波模型、神经网络模型,粒子群优化结合方式实现了组合预测模型的建立。沉降数据时间序列首先通过小波函数进行去噪处理,处理之后的数据作为神经网络模型的输入向量,建立小波-神经网络预测模型;随后通过粒子群与BP神经网络结合建立小波去噪的粒子群优化算法(prticle sarm otimization,PSO)-BP神经网络(back propagation neural network)模型,二者预测结果进行对比分析。

1 BP神经网络理论基础

BP神经网络模型是由国外专家学者领导的课题组于1986年建立并广泛推广使用的不需要具体详细描述输入值与输出值之间的映射关系[4-6]。只需要通过非线性的内部映射处理,实际输出值与期望输出值不间断比较,反向通过传播误差来调节阈值与权值,重新输出与输入。通过不间断地非线性映射由输出层逐渐与期望值不断减小误差的一种模型。在文中列举的某一地铁一号线实测沉降数据建模前,将沉降数据序列统一做处理,通过归一化处理能够降低由于大数值的存在导致模型不收敛的情况发生。归一化计算方法如式(1)所示。

(1)

式中,x*是处理之后的数值;xi是外业获取数据;xmin、xmax分别是沉降序列数据中的最小值、最大值。将处理之后数据还原为

(2)

2 小波分析多尺度分解原理

对原始输入数据信号进行多尺度分解细化,依靠小波分析方法中的小波基函数伸缩平移运算来实现。其中小波基函数由一组有限长不断缩放、平移组成。依靠小波基函数方法对原始数据信号进行分解时,分离出来的低频信号具有很强的稳定性以及平滑性能优异,这组信号能够表现出原始信号的趋势[7-10]。利用小波进行分解为

(3)

式中,a为尺度因子;b为平移因子；φ(a,b)(t)是有小波母函数生成的连续小波。则相应利用Wf(a,b)重构f(t)为

(4)

式中,Cφ为小波基函数。关于选择合适的软硬阈值与小波基函数,文章4.1小结将通过数据验证最优的小波基函数。

3 粒子群优化的BP神经网络原理

3.1 参数控制

(1)本文涉及了BP神经网络模型采用三层层次架构,分别为输入层、隐含层、输出层。

假设In为输入层节点个数,Ou为输出层节点个数。为确定隐含层节点个数可采用如式(5)所计算方法,该公式是经验公式,通过合理的确定隐含层节点个数来提高学习效率与增强学习样本能力[11]。

(5)

其中,Mi为隐含层节点数目；α为1～10之间的自然数。

(2)粒子算法中权重w计算方式采用递减线性方式,详细见式(6),而其中c1和c2加速因子采用经验方式计算获取[12-15],详见式(7)和(8)。

其中,cl为当前迭代次数；wmax=0.95,wmin=0.25；Ma为总迭代代数；c1s=2.75,c1e=1.25,c2s=0.5,c2e=2.25。

(3)适应度函数。本文提到的BP神经网络模型是一种称之为前馈神经网络的简称,该模型通过输出层误差反向传递来逐层修正各层之间的权值与阈值,满足收敛条件为止,文中粒子群算法中适应度函数计算式(9)所示。

(9)

其中,Q代表训练样本数;y代表神经元输出的实际值;t代表神经元的期望值。

3.2 组合算法描述

粒子群算法与BP神经网络算法相结合,其主要是吸取二者在各方面的优势来提高组合算法的寻优能力,这就包括BP神经网络模型中阈值与权值优化,模型拓扑结构的优化，等等。这将粒子群算法的全局寻优能力得到重点细化,以提高神经网络的泛化能力和学习性能,从而改进神经网络的整体搜索效率[15]。本文将二者结合的模型称之为PSO-BP神经网络模型。详细组合算法过程如下所示。

(1)优先确定BP神经网络算法的结构层次关系,以及各阈值、权值包括输入层、隐含层、输出层数目的确定,以此来确定粒子群算法中各最优参数,根据结构确定粒子群维数的数目。

(2)确定粒子群模型中的适应度函数。

(3)将粒子群中的各维度中粒子进行初值设置。

(4)在BP神经网络中的权值与阈值确定过程中,为搜寻最优值,本文将粒子群中的适应度算法中顾及的最小值,利用此最小值作为粒子中数值。依靠该最小值通过不断迭代计算,来找到粒子的最优位置。该位置对应的数值就为权值与阈值的最优初始值。

(5)将上一步骤确定的权值与阈值最优初始值引入到BP神经网络模型中,随后开始预测工作,根据确定的阈值来判断迭代次数,最终能够达到最优预测结果。

4 实例应用

4.1 项目概况

某城市地铁一号线位于该城市主干道正下方,施工中采用盾构法。实验区域选在东西两条主干道所在中间路段,该路段车流量巨大,行人众多,并且沿路周边屹立高大写字楼。为保障地铁安全施工,减少对周边行人、车辆以及建构筑物的威胁,我单位受委托进行定期对地表沉降进行监测。实验区域范围及基准监测点位置如图1所示。

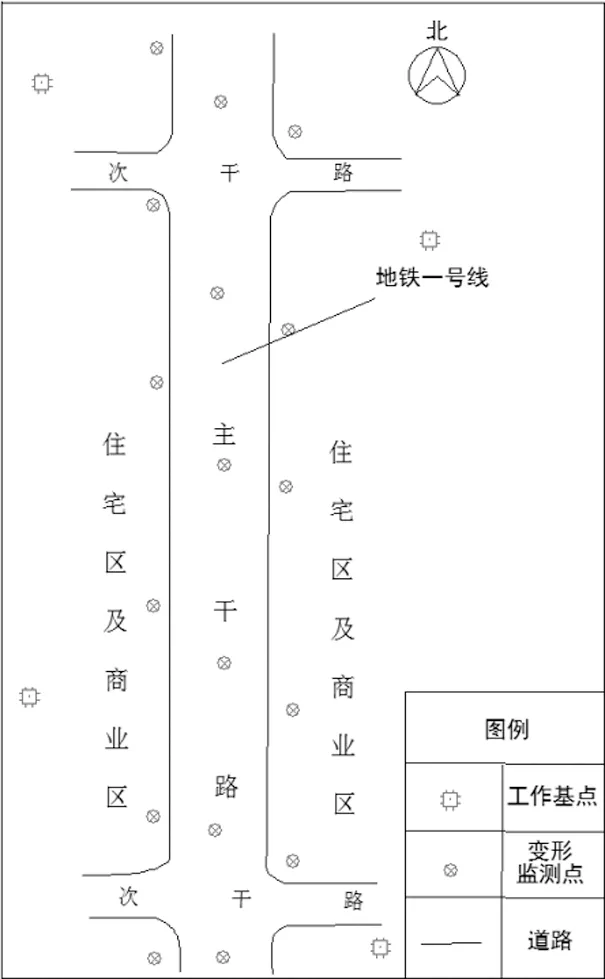
图1 测区位置与监测点分布图

2019年11月10日开始对该市政道路进行监测工作,目的是按照相关测量规范和设计的要求进行变形监测,道路两边之上按照一定原则布设监测点,可采用水准仪加水准尺等测量方式对其进行周期性观测,及时掌握路边地表沉降位移及应力变化情况,分析其变形规律和变形趋势,为地铁的安全建设和运营提供保障。截至2021年4月30日,共完成监测工作81次。

4.2 数据获取

测量技术人员在沿路周边稳定区域布设了4个监测基准点和4个工作基点,并在沿路主要地点布设了66个变形监测点。对地表沉降变形监测项目使用高精度的莱卡DNA03电子水准仪,按照作业指导文件中规定的操作来进行外业测量,在合乎观测过程中获取每个变形监测点的沉降数值。从2019年11月17日至2021年4月30日,总计外业获取了81期的观测数据,其中以“40”号监测点为例,实测数据如表1所示。

4.3 小波去噪在沉降监测中的实例

对该道路沉降监测数据进行建模处理,其中小波基函数中软阈值与硬阈值函数的选择时,不同阈值具有不同的调整方式，scal=min、scal=one和scal=sln,使用以下两种小波基函数DbN和SymN对观测数据进行小波分解分层与小波去噪处理。经过数据对比分析均方跟误差与不同小波基函数的信噪比,经过比较得出了小波基函数sym4与软阈值方式、小波1层分解、scal=sln最适合。波基函数软阈值一层分解,scal=sln函数中依次对表格1中出现的四种阈值进行去噪处理。四种阈值包括rigrsure、heursure、minimaxi、sqtwolog,比较见图2。表格1展示了均方根误差(root mean squared error,RMSE)值与信噪比(signal-to-noise ratio,SNR)值比较情况。

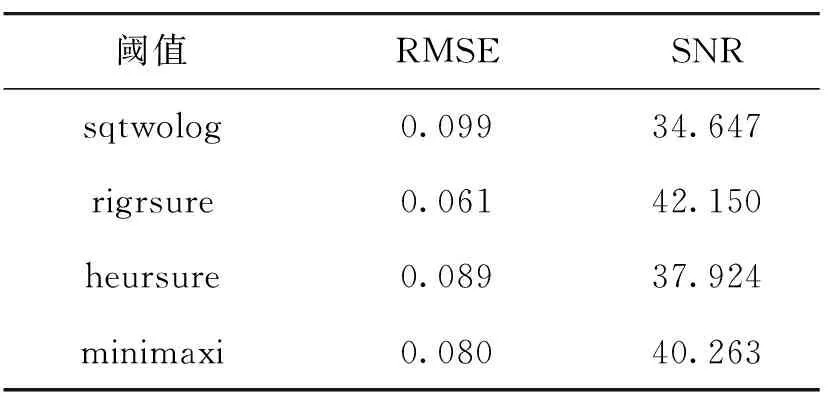
表1 不同阈值去噪效果比较

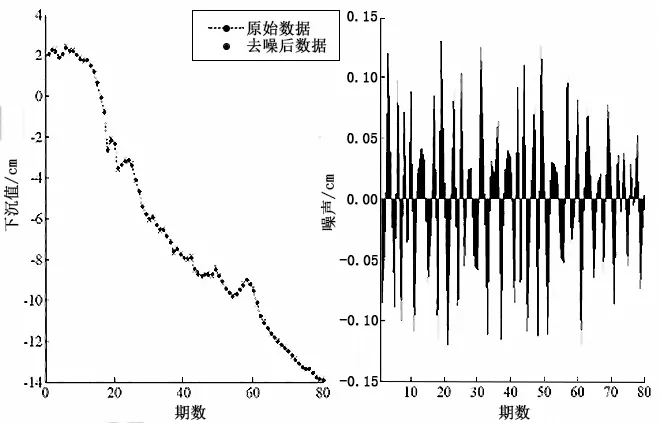
(a)rigrsure

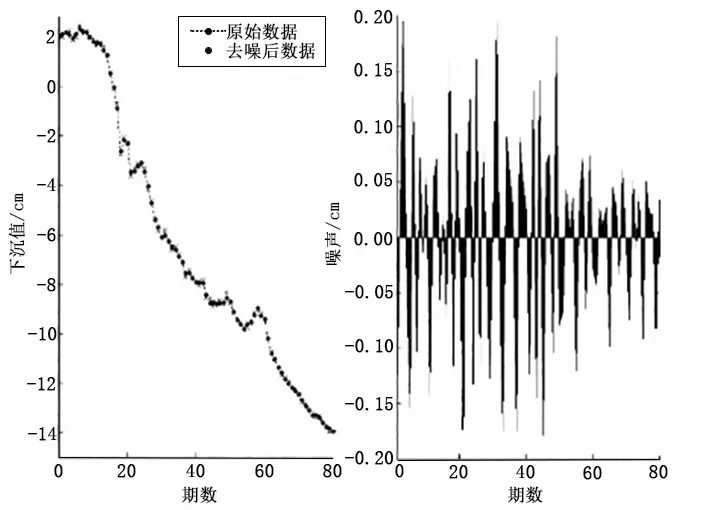
(b) heursure

(c)minimaxi

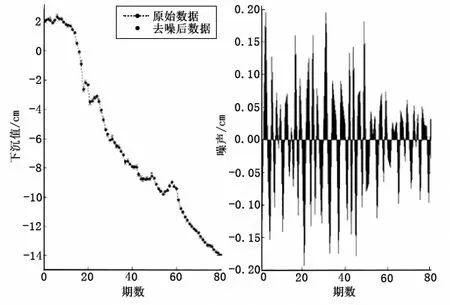
(d)sqtwolog图2 四种阈值函数去噪对比图

由表格1统计数据可获知,rigrsure阈值函数去噪效果中均方跟误差为0.061,信噪比数值为42.150。由表格中数据对比可知，rigrsure阈值函数均方根误差最小,信噪比数值最大。综上所述rigrsure阈值函数去噪效果最好,所以在对沉降监测观测数据去噪处理中,选择rigrsure阈值函数进行去噪处理大大增强了BP神经网络模型的预测效果。

4.4 BP神经网络模型训练

本小节以沉降监测线上监测点“40”号的81期观测沉降数据为例,在BP神经网络中训练形成的响应函数,防止出现“过拟合”现象。考虑到该现象给预测模型带来的问题,本文将该监测点81期的观测数据分成三组样本,分别是训练样本、验证样本、测试样本。BP神经网络模型通过训练样本训练算法层次,依靠验证样本来检验模型收敛程度。“40”号监测点的前70期沉降数据组成了训练数据集,解算过程中产生的均方误差曲线如图3所示。由图3可知,经过863次的迭代训练,图中曲线收敛于10-5,此时将自此训练效果认定为良好。之后对该点前1～70期数据进行实验处理,构建BP神经网络模型,并与经过小波去噪之后的数据构建BP神经网络模型对比。以71～81期数据为参考,对比两种方法的预测精度,比较结果如图4所示。

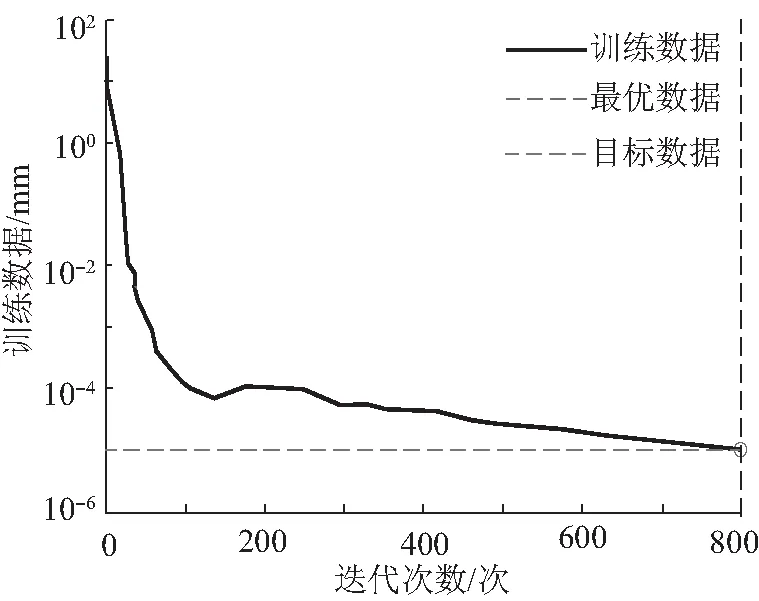
图3 训练样本均方误差图

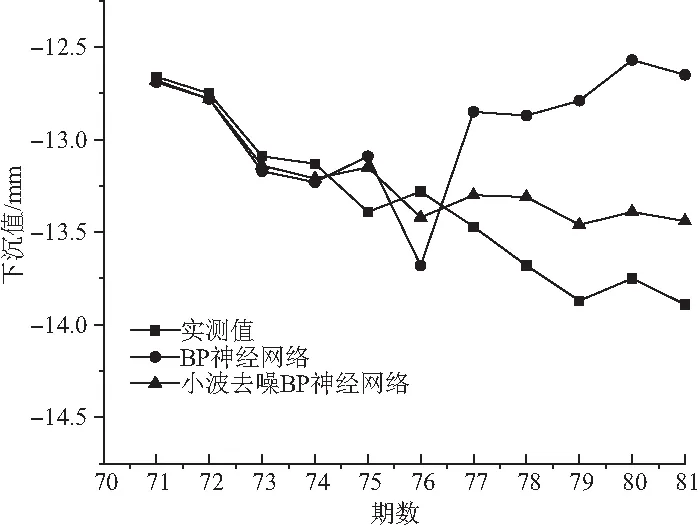
图4 两种方法与实测数据比较图

由以上两图可总结出原始数据经过小波去噪之后,建立BP神经网络模型预测效果得到提高,这对提高神经网络预测能力有很大帮助。

4.3 粒子群优化的BP神经网络应用

本小节采用沉降监测区域内“40”号监测点沉降观测数据为例,采用PSO-BP神经网络预测模型进行预计工作。首先选取前70期沉降观测数据序列进行小波去噪工作,而后对后11期沉降观测数据进行预测。分别进行三种模型预测比较,并于以实测值曲线作为参考。预测效果与各模型间比较如图5和图6所示。

图5 三种模型预测比较图

图6 各模型间预测误差比较图

由以上两图可总结出,BP神经网络模型前期预测效果较好,小波去噪的BP神经网络模型预测前期效果与其相当,小波去噪的PSO-BP神经网络模型略微优于二者。但随着预测期数的递增,BP神经网络模型、小波去噪的BP神经网络模型预测精度逐渐降低,小波去噪的PSO-BP神经网络模型预测精度递减较慢,同时小波去噪的PSO-BP神经网络模型预测值与实际观测值偏差较小且稳定,说明了小波去噪的PSO-BP神经网络模型不但适用于短期预测,也同样适用于长期预测。表2展示了三种预测模型的精度统计结果。

表2 预测结果对比表

由表2统计精度可知,总体上这三种模型预测精度最高的是小波去噪PSO-BP神经网络模型,预测精度最差的是BP神经网络模型,小波去噪BP神经网络模型处于中等水平。

从表格2还知,小波去噪BP神经网络模型、BP神经网络模型这两种预测模型的预测精度随着预测期数的增加预测效果逐渐变差,由此也反映出了这两种模型较适合于短期预测;小波去噪PSO-BP神经网络模型预测精度随着预测期数的增加相交于稳定,又一次证明了该模型适用于短期预测、长期预测。

5 结束语

本文考虑到常规BP神经网络模型中存在的不足,引用粒子群与小波去噪二者的优点,得到一种小波去噪的粒子群优化BP神经网络预测组合模型。使用该组合模型并结合地铁施工中地表沉降监测数据,进行预测分析。预测精度统计结果表明,短期预测中小波去噪PSO-BP神经网络模型预测精度水平一般,但随着预测期数增加,其预测优势逐渐凸现,并通过实际案例验证了这一结论。但在长期预测中,该组合模型有待验证,并在以后的工作中尝试利用该组合模型应用在其他领域的沉降预测工作。