基于离散平稳小波的影像恢复去噪方法

王 昶 郭东升

(1. 辽宁科技大学 土木工程学院, 辽宁 鞍山 114051; 2. 铁岭市自然资源事物服务中心, 辽宁 铁岭 112008)

0 引言

遥感图像作为获取地物信息的重要手段,被广泛应用于环境监测、资源普查、城市规划、灾害评估、军事侦察等诸多领域。然而受工作环境、成像设备等因素的影响,遥感图像在成像、传输与存储过程中,会不可避免地受到噪声的污染。由于遥感图像存在噪声,导致遥感图像包含的重要信息被覆盖,直接影响遥感图像的视觉效果及计算机对遥感图像的后续处理。

目前,研究学者提出了许多图像去噪的算法,如基于滤波方法[1-6]、基于小波阈值方法[7-8]、基于偏微分方程方法[9]、基于变分方法[10]及基于稀疏表达方法[11]等。上述图像去噪理论虽然一定程度上抑制了图像噪声,但同时也存在一些不足。基于滤波方法,此方法在去除图像随机噪声的同时会丢失较多图像边缘细节信息,导致去噪图像模糊;小波阈值去噪方法,虽然该方法能在变换时间域和频率域时具有良好的局部化特性,并且具备图像边缘的检测能力。但由于阈值会根据不同的判断准则被选取,如果阈值选取过大,会使图像的部分有用信息丢失,如果阈值选取过小,则去噪效果不明显;基于偏微分方程方法,早期Perona等人提出了彭曼-蒙特斯(Penman-Monteith,P-M)模型。此方法在图像去噪过程中,不能很好地保留图像细节信息,且该模型存在病态性问题,无唯一解,需要引入正则项;基于变分方法,Rudin等人提出了经典的ROF(Rudin-Osher-Fatemi)模型或整体变分(total variation,TV)模型。虽然该模型在去除图像噪声的同时能够很好地保持图像的边缘,但在图像平稳区域容易产生阶梯效应,并且噪声也会被作为图像特征保留在图像的边缘中,从而形成新的图像边缘;基于稀疏表达的算法,如Aharon等人提出了奇异值分解(Kmeans-singular value decomposition,K-SVD)方法[12],此方法侧重于噪声的平滑,从而导致去噪图像模糊,图像边缘细节信息丢失比较多。

上述算法在图像去噪过程中,无法同时做到即能有效去除图像噪声又能很好地保留图像边缘细节信息。针对此问题,本文提出一种基于离散平稳小波(stationary wavelet transform,SWT)的图像恢复去噪算法。此算法是把SWT及构建的图像恢复模型相结合来去除图像噪声的。为了避免图像去噪过程中图像边缘细节信息大量丢失,采用SWT分解噪声图像,使图像边缘细节信息有效地分离出来;为了能够达到有效去除噪声的同时保留更多图像边缘细节信息的目的,本文采用构建的图像恢复算法对每一层高频分量进行去噪处理。通过对不同的噪声遥感影像进行去噪处理来验证此算法的性能。

1 构建图像恢复模型

1.1 图像恢复模型的扩散原理分析

图像恢复正则化模型的通用表达式为[13-14]

(1)

(2)

(3)

下面对上述方程进行扩散能力分析,首先将图像局部结构进行分解,建立直角坐标系(τ,n)。在局部坐标系下,式(3)写成

(4)

其中,

1.2 算法优化

对式(2)求解能量泛函极值问题,可以转换为求解对应的欧拉-拉格朗日方程的解,即

(7)

式(7)对应的欧拉-拉格朗日表达式为

(8)

对于图像边界上的点采用Neumann边界条件

(9)

对式(8)可以利用有限差分法进行离散化,设定k为空间步长,一般取k=1。为了刻画水平与垂直方向的离散导数,引入标记,让D+x、D-x、D+y、D-y、Dx0、Dy0代表差分算子,用加号表示向前有限差分算子,用减号表示后向有限差分算子,Dx0、Dy0表示中心差分算子。则有

(10)

式(8)得到的离散化形式为

(11)

对式(11)采用不动点Gauss-Seidel迭代法进行求解，见式(12)。

(12)

式(12)可得式(13) 。

(13)

2 实验与分析

本文选择两幅遥感影像作为实验数据,并在这两幅遥感图像上添加噪声标准差δ为20的随机噪声,如图1所示。

(a)纯净遥感图像1

(b)加噪遥感图像1

(c)纯净遥感图像2

(d) 加噪遥感图像2图1 纯净遥感图像与加噪遥感影像

2.1 图像随机噪声去除2.1.1 小波基函数的选取及分解层数确定

对噪声遥感图像进行SWT分解之前,小波基函数的选取尤为重要。为了说明本文小波基函数选取的正确性,本文采用5种常用的小波基函数(haar、db2、sym2、coif2、bior1.3)对纯净图像进行一层SWT分解,以分解得出水平方向高频分量。为了方便表示,论文用h1表示为水平方向高频分量,如图2和图3所示。

(a)haar-h1

(b)db2-h1

(c)sym4-h1

(d)coif2-h1

(e)bior1.3-h1图2 不同小波基函数对纯净影像1一层分解的水平方向高频分量示意图

(a)db2-h1

(b)haar-h1

(c)sym4-h1

(d)coif2-h1

(e)bior1.3-h1图3 不同小波基函数对纯净影像2一层分解的水平方向高频分量示意图

通过图2和图3可以清晰地看到,纯净遥感图像经db2、sym2及coif2一层分解获得的高频分量所显示的图像边缘细节信息失真程度比haar和bior1.3小波基函数大。又由于haar具有正交性及对称性,而bior1.3不具备这两种特性。综合比较,在本文方法中选择haar小波基函数。

小波分解的层数主要以经SWT分解出的高频分量是否含有噪声为依据来确定的。通过实验分析,经SWT第四次分解获得的高频分量已不受噪声的污染。因此,本文确定小波分解的层数为3层。

2.2.2 遥感图像随机噪声去除

本文对低频分量及去噪后的高频分量进行SWT重构,获得去噪图像。并与传统TV模型[10]、目前公认去噪效果较好的三维块匹配滤波(block-matching and three-dimensional filtering,BM3D)模型[15]及K-SVD模型[12]进行比较,实验结果如图5所示。

(a)纯净影像1

(b)TV

(d)BM3D

(e)本文算法图4 不同去噪算法对影像1去噪效果示意图

(a)纯净影像2

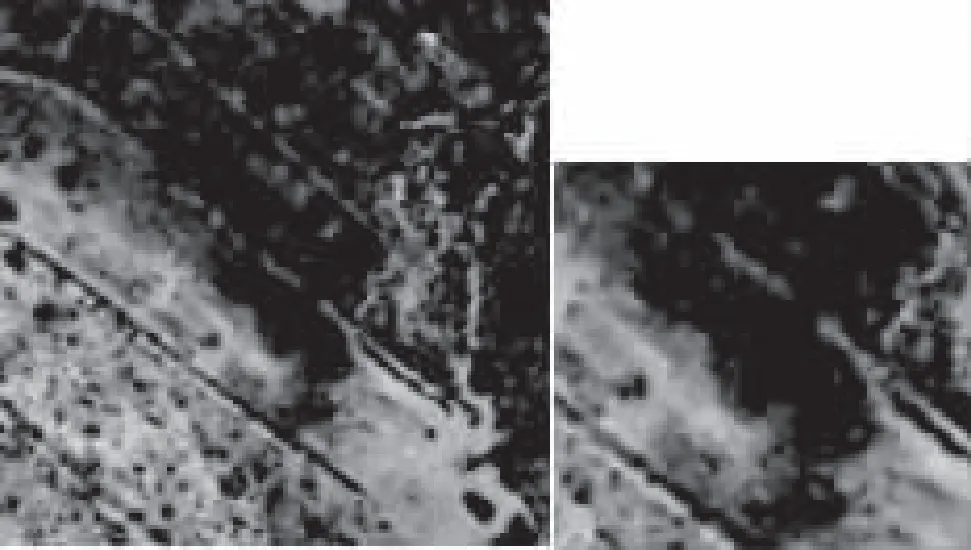
(b)TV

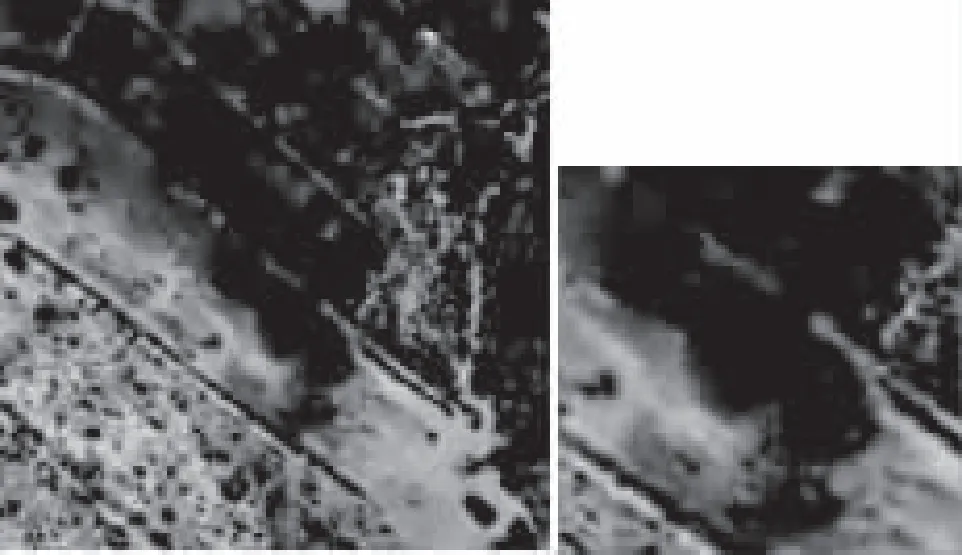
(c)K-SVD

(d)BM3D

(e)本文算法图5 不同去噪算法对影像2去噪效果示意图

从图4和图5可以看出,上述不同去噪算法在一定程度上抑制了图像的随机噪声。经传统TV算法去噪后,两幅实验影像去噪后中许多边缘细节信息被保留,但图像出现了明显的阶梯效应,第一幅实验影像尤为明显。经K-SVD和BD3M算法去噪后,两幅实验影像去噪后出现明显模糊现象,说明K-SVD和BM3D去噪算法侧重于随机噪声的平滑,图像边缘细节信息丢失较多。本文提出的去噪算法,不仅可以有效地抑制图像的随机噪声,而且保留更多图像的边缘细节信息,两幅实验影像去噪后无明显模糊现象及阶梯效应,并且图像呈现较好的视觉效果。

本文采用峰值信噪比(peak signal to noise ratio,PSNR)和结构相似性(structural similarity index method,SSIM)两种图像去噪评价指标来衡量上述各种图像去噪算法的效果,见表1。

表1 不同图像去噪算法评价指标结果

从表1可以看到,传统TV去噪算法的PNSR值小于K-SVD和BD3M算法,但SSIM值高于这两种算法。说明传统TV算法能够更多地保留图像边缘细节信息,但去噪效果相对较差。而K-SVD和BD3M虽然去噪效果比较好,但是以丢失更多图像边缘细节信息为代价的。本文算法的SSIM值和PSNR都高于传统的TV算法、BD3M算法及K-SVD算法。说明本文提出的去噪算法不仅可以有效地抑制图像的随机噪声,而且能保留更多图像的边缘细节信息。

为了验证本文算法的稳定性,继续在两幅遥感图像上添加噪声标准差δ为25、30的随机噪声,实验结果及图像去噪客观评价指标见图6和图7及表2。

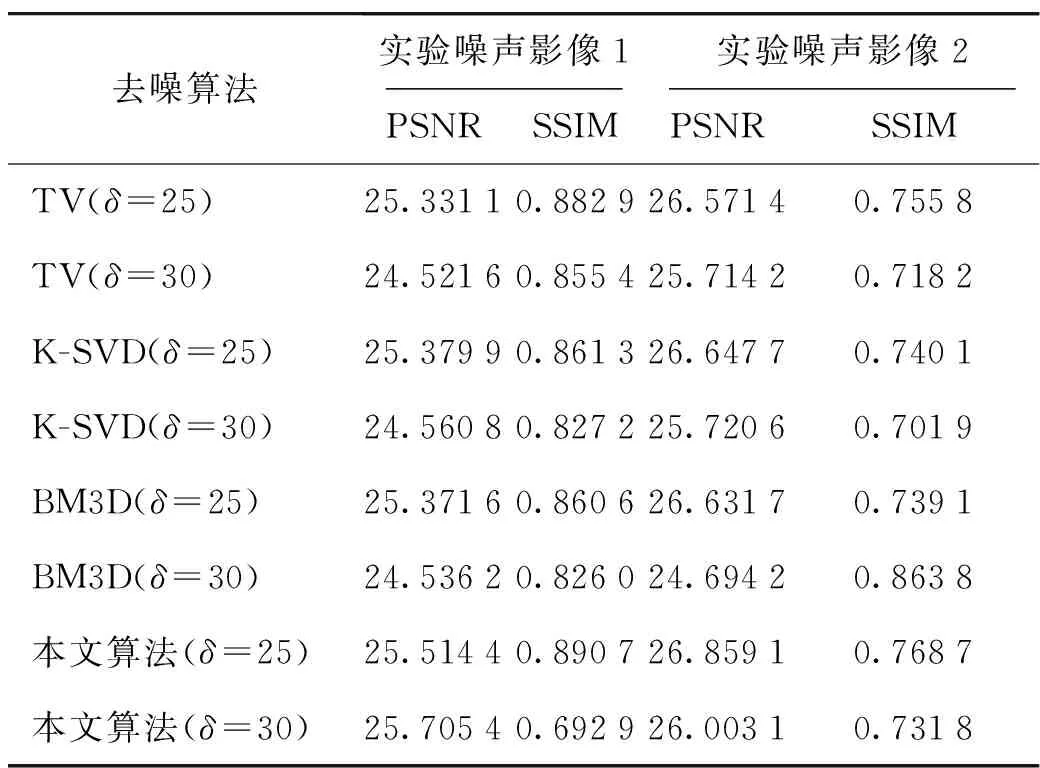
表2 不同图像去噪算法评价指标结果

(a)纯净影像1

(b)TV(δ= 25)

(c)K-SVD(δ= 25)

(d)BM3D(δ= 25)

(e)本文算法(δ= 25)

(f)TV(δ= 30)

(g)K-SVD(δ= 30)

(h)BM3D(δ= 30)

(i)本文算法(δ=30)图6 不同去噪算法对影像1去噪效果示意图

(a)纯净影像2

(b)TV(δ= 25)

(c) K-SVD(δ= 25)

(d)BM3D(δ= 25)

(e)本文算法(δ= 25)

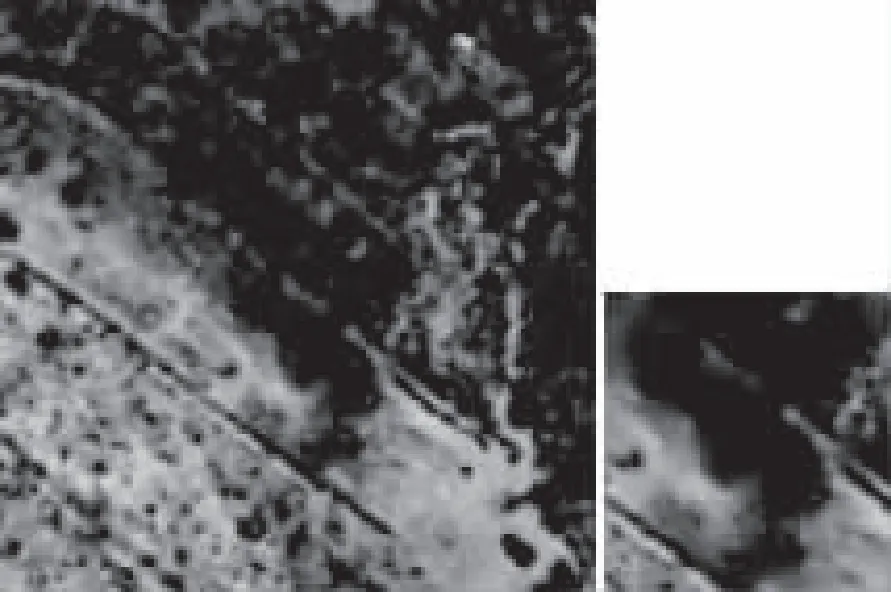
(f)TV(δ=30)

(g)K-SVD(δ= 30)

(h)BM3D(δ= 30)

(i)本文算法(δ= 30)图7 不同去噪算法对影像2去噪效果示意图

3 结束语

为了在去除噪声的同时保留更多的影像细节信息,本文提出一种基于离散平稳小波的图像恢复去噪方法。通过离散平稳小波分解噪声影像,使图像边缘细节信息有效地分离出来。通过构建的同性扩散及异性扩散能力的图像恢复算法可以有效去除高频分量的噪声,同时保留更多影像细节信息,同时避免去噪图像产生阶梯效应。通过与其他方法比较,本文方法不仅能够有效去除噪声,而且在保留影像细节方面是较好的。