多尺度点云滤波去噪方法

刘翔宇 宋 羽

(1. 山东科技大学 测绘与空间信息学院, 山东 青岛 266590; 2. 济南市勘察测绘研究院, 山东 济南 250013)

0 引言

由三维激光扫描仪直接获得的点云数据在实际应用之前往往需要进行一系列的优化处理,低质量的点云数据会对其应用、分析造成巨大的影响[1]。在点云滤波去噪领域,中值滤波与高斯滤波最早被应用于噪声的滤除[2],其中,中值滤波通过对当前采样点与其邻域点进行均值计算,将计算出来的均值点作为当前点的位置,原理相对简单,但易产生新的噪声且滤波效果不佳。由于改变了点云位置,无法保持点云细节特征;高斯滤波通过对点云及其邻域点距离进行加权处理,按距离大小分配权重,根据其大小判断噪声,其方法在细节特征上有所保留,但滤波效果不佳,特别是密集型噪声难以去除。Yagou等[3]采用网格滤波的方式,对网格法线应用均值滤波和中值滤波,然后更新网格顶点位置,以使网格适应修改后的法线,该方法虽然对噪声有明显的滤除效果,但易发生形变。Desbrun等[4]针对拉普拉斯滤波算法的弊端做相关研究,提出了基于平均曲率流的方法,在滤波过程中使顶点的移动沿着法方向进行,有效地避免了顶点漂移。但是这种方法会导致尖锐点部分点云特征无法得到很好地保持。为避免上述情况的发生,Clarenz等[5]通过求解离散的各向异性扩散方程,实现了点云滤波。梁新合等[6]结合点云实际特征,利用三边滤波算法做到了研究区域自适应的滤波降噪。叶珉吕等[7]将最小二乘拟合的点云模型与点云进行距离探测,通过设定阈值判定噪声,但局限性较大,且难以保持精度。Fleishman等[8]提出了一种快速的、基于二维双边滤波图像去噪原理的各向异性三维点云滤波去噪算法,通过使用局部邻域在法线方向过滤网格顶点的方式,对传统滤波算法边缘特征难以保留的缺陷进行了改进,但复杂度较高,对于复杂噪声的处理情况并不理想;王丽辉等[9]将聚类算法与双边滤波算法相结合,提出了通过模糊C均值(FCM)聚类算法实现大尺度噪声去除并通过双边滤波方法进行精细化去噪的点云滤波方法;曹爽等[10]通过对点云网格化,采用基于特征选择的方式将点云分为特征点与非特征点,采用不同的滤波参数进行去噪,虽然可以进一步保证点云边缘特征,但操作复杂,鲁棒性不强;袁华、李明磊[11-12]等先后在双边滤波算法的基础上进行改进,并在自己的研究领域取得了不错的成果;韩浩宇等[13]给出了一个结合双张量投票和多尺度法矢量统计的点云滤波算法,该方法在有效剔除噪声点的同时保留了点云模型的尖锐特征。

针对上述问题,本文在结合现有去噪算法的基础上,研究一种多尺度点云去噪算法,期望解决传统点云滤波算法会丢失物体细节特征的问题,为后续点云配准与点云重建提供基础。

1 理论方法

1.1 基于统计分析的大尺度远离群点去噪方法

大尺度噪声主要指位于主体点云附近的离散稀疏点云或距离较远的小型密集点云,从点云整体看,主体点云多而集中,噪声点云小而分散[14],本文基于统计分析的去噪方法就是利用主体点云点与邻域点间的距离小、离散点云到邻域点间的距离大的特点来实现对于离散点的判别。即通过计算采样点到邻域点集的距离进行统计分析进而进行离群点的判别,去除无用噪声。

基于统计分析的点云去噪方法的具体流程如下：

(1)设定采样点集P={pi∈R3|i=1,2,…,n},其中,对任一点pi的邻域内有k个临近点,即其K邻域,记为Pij={pi1,pi2,…|j=1,2,…,k}。

(2)设定K邻域的大小,计算采样点pi到其K邻域的平均距离ui,如式(1)所示。

(1)

(3)重复计算所有采样点,得到每个采样点到设定K邻域的平均距离,通过计算得到全局平均距离un与标准差σ,如式(2)与式(3)所示。

(4)设定标准差倍数阈值std,得到距离阈值un±σ·std,对每一个采样点pi到K邻域的距离ui与全局平均距离un进行判定,对ui>un的点进行去除,反之保留为主体点云。

1.2 基于小尺度的近离群点去噪方法

本文基于引导滤波原理将其从二维像素扩展到三维点云,实现点云的近离群点去噪。两种方式都具备一致的思想：在梯度变化较大的地方实现保留,尽量不平滑;而在梯度比较小的地方,进行平滑滤波。在三维空间中,根据引导滤波的基于局部特征的原理,将二维图像中通过梯度变化识别边缘区域改进为通过判定点云邻域协方差矩阵大小进行判定边缘区域,具体原理如下：

(1)通过KD-tree数据结构来构造点云,通过K邻近分类(K-nearest neighbors,KNN)确定其邻域N(pi)。

(4)

式中,|N(pi)|为N(pi)的基数。

(4)由协方差矩阵∑i与参数,计算线性因子根据协方差矩阵反应点云形态变化程度：当处于平坦区域时, ∑i≪,则ai≈0,做均值滤波,处于边缘区域时,∑i≫,ai≈1,bi≈0,基本保留点云边缘特征。最终实现自适应滤除平缓区域点云,保留点云边缘特征。

(5)通过对每个点计算与其邻域进行线性变换求取pi在自身邻域N(pi)中的滤波点,进行局部滤波去噪。

1.3 多尺度点云滤波方法

通过将离群点划分为远距离的大尺度噪声与近距离的小尺度噪声,利用统计分析原理高效的特点,初步、快速去除较远位置的点云,降低其干扰,进而进行局部滤波,将图像引导滤波算法拓展到三维点云中,去除近离群点点云,通过点云及其邻域的协方差矩阵大小,反应点云局部形态变化,最大限度上降低滤波对于原始点云数据的影响,保证后续点云应用的精度。具体流程如图1所示。

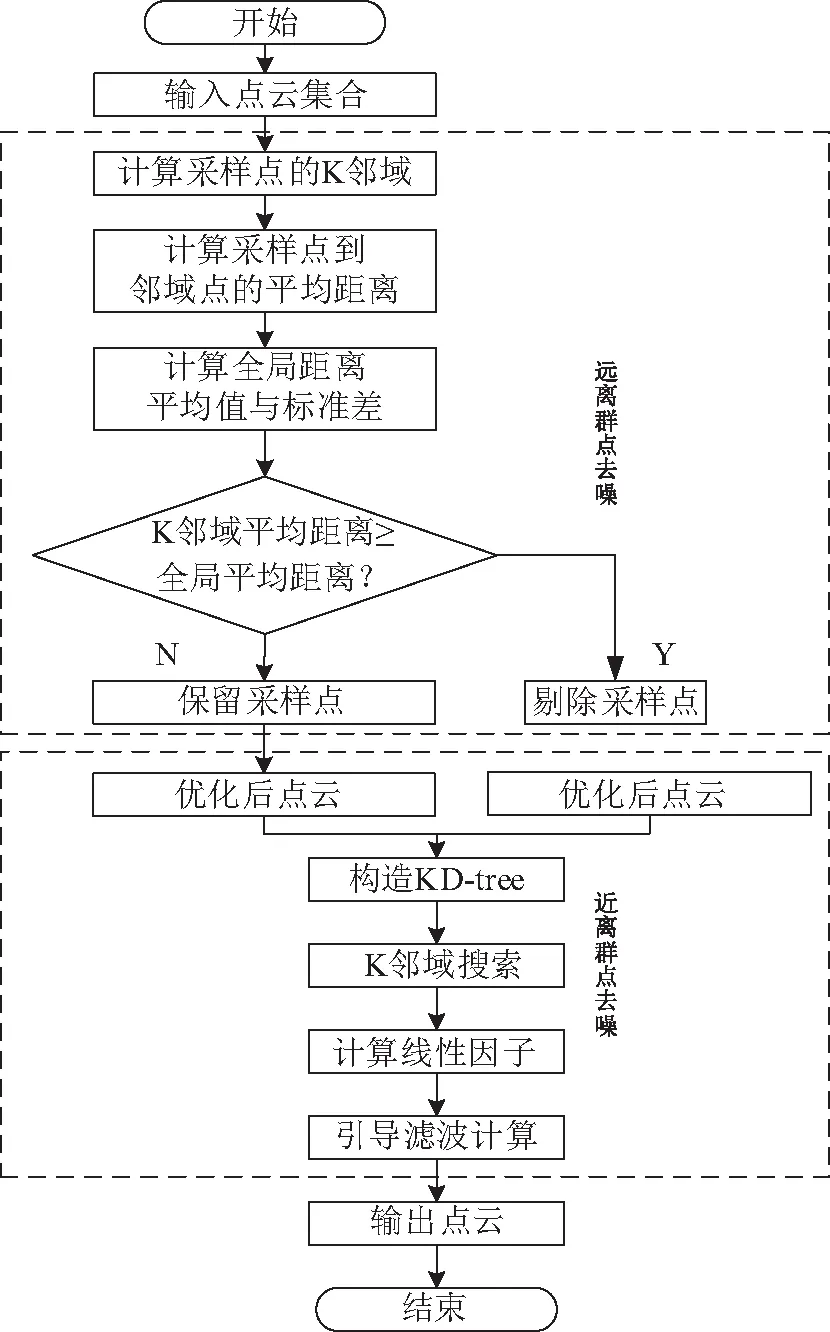
图1 算法流程

2 实验验证

为验证本文算法,选取斯坦福大学的标准Chair点云模型数据和某实测土坡数据,并对标准点云数据进行加噪处理,如图2所示,在点云附近0～5 mm、50～55 mm以及更远区域分别添加一定量的噪声,模拟远近不同距离的离群点。

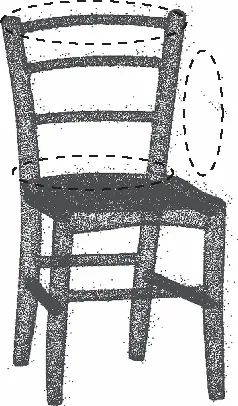
(a)加噪Chair数据

(b)坡体整体数据图2 实验数据

针对两种点云数据分别使用统计滤波、半径滤波。双边滤波和本文算算法进行去噪处理,具体如图3、图4所示。

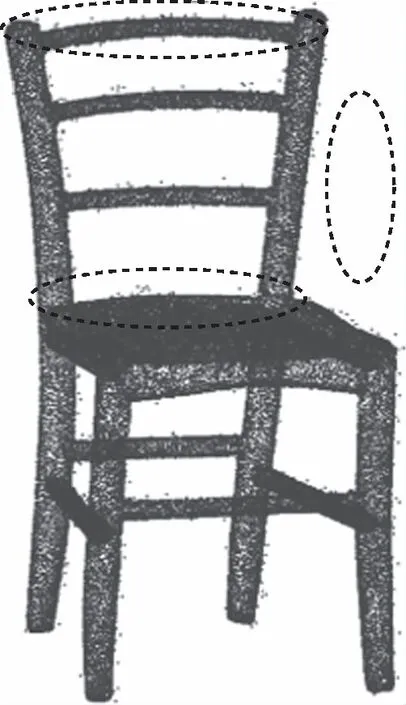
(a)统计滤波

(b)半径滤波

(c)双边滤波

(d)本文算法图3 Chair点云滤波效果对比

(a)统计滤波

(b)半径滤波

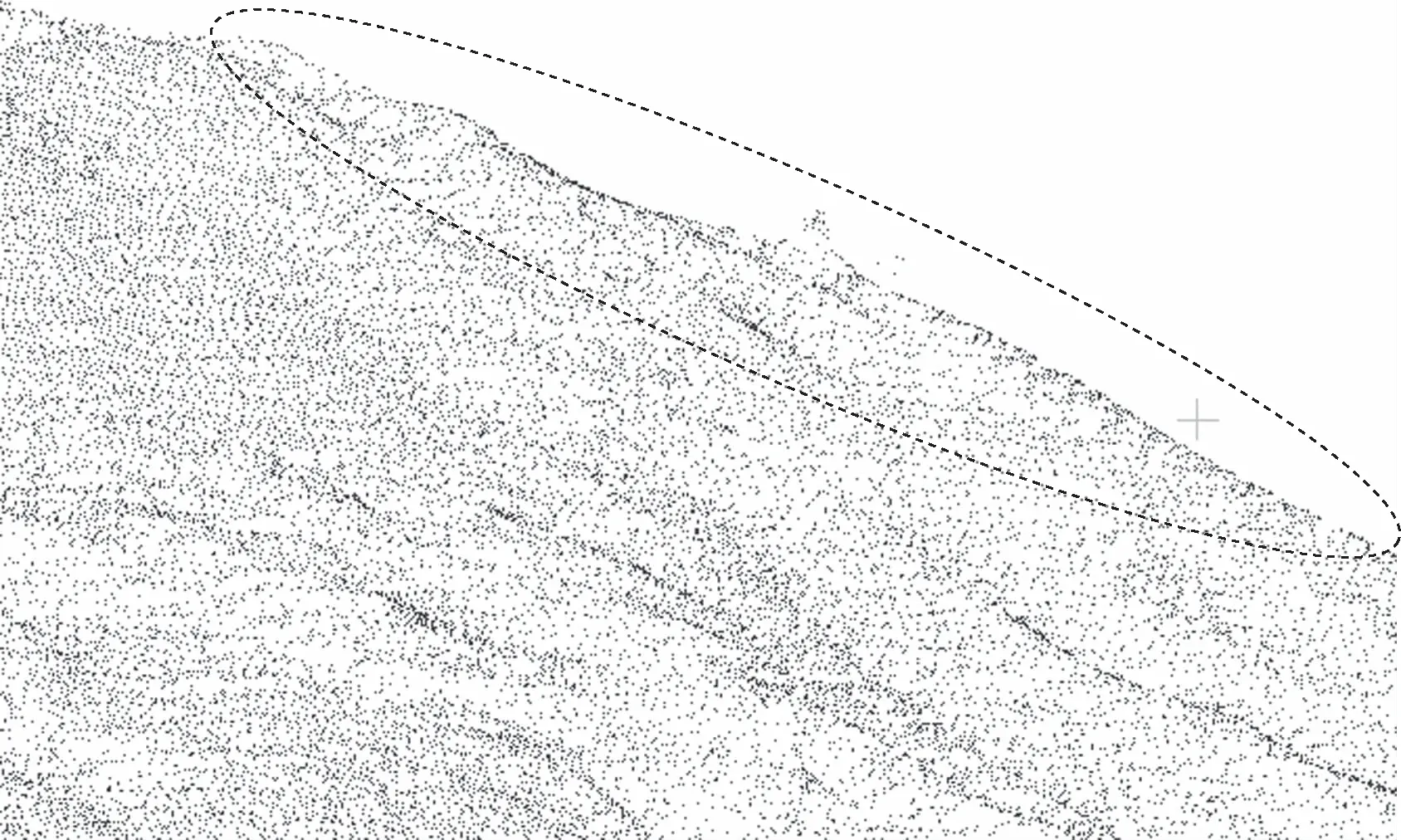
(c)双边滤波

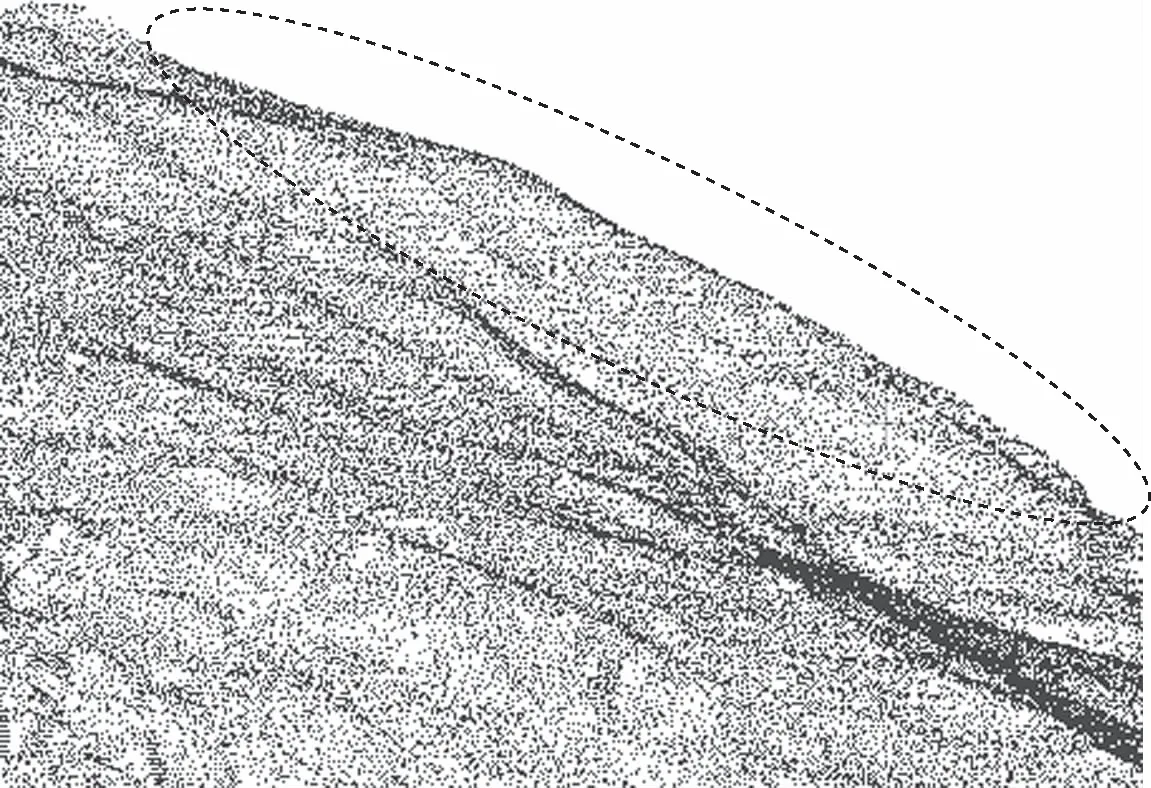
(d)本文算法图4 坡体点云滤波效果对比

从图3(a)和图4(a)可以看出统计滤波对较远位置的离群点可以有效地去除,但是对于分布在主体点云附近的近距离离群点去除效果较差。分析图3、图4中的(b)(c),采用半径滤波根据检索半径和判定半径区域内临近点的个数是否符合阈值来进行离群点的判定,虽然可以有效地去除噪声,但由于近离群点距离主体过近,会产生错误的判断,造成主体点云缺失,严重影响精度。双边滤波虽然在近离群点处效果较好,也能够一定程度上保持边缘特征,但存在局部区域过渡平滑、精度丧失的现象。通过分析图3、图4中的(d)可以看出本文算法可以有效去除近离群点噪声,同时最大限度上完整保留点云的边缘信息,降低噪声对精度的影响。

3 结束语

本文针对在使用传统滤波方法进行去噪时,不能兼顾滤波效果与保留细节特征,会造成精度丢失的问题。采用基于统计分析的点云去噪方法去除大尺度噪声,结合图像引导滤波原理去除小尺度噪声。最后选用标准Chair数据和实测某土坡数据进行实验验证,实验结果表明本文算法在保留特征、去除远近离群点上效果较为明显,对实测点云数据具备较好的适应性。