基于碎点法的动态断裂分析1)
沈宝莹 王松 李明净 董雷霆
(北京航空航天大学航空科学与工程学院,北京 100191)
引言
冲击防护结构广泛存在于航空航天、汽车、船舶、核能乃至国防等工程领域.这类结构在抵抗如撞击、爆炸等极端的冲击载荷时可能会发生动态断裂直至最终破坏.准确预测结构在动态载荷下的断裂破坏行为对防护结构的设计和改进具有重要意义.数值仿真方法是预测结构动态断裂的重要手段,学者在这个方面已经进行了长期、大量的研究,然而由于动态断裂问题的复杂性,这仍然是计算固体力学领域一个具有挑战性的研究方向.
有限元法是当前工程领域应用最广泛的数值仿真方法,有限元法基于伽辽金弱形式且使用可以使用简单多项式的形函数,具有稳定性强、数值积分简单等优点[1].然而有限元法在模拟动态断裂导致的结构破坏时存在两个方面的难题.第一个方面,有限元法本质上是基于位移连续性假设的,因此难以在模型中显式引入裂纹.当前解决这个问题的一种方法是使用网格删除技术,然而删除网格会导致和物理过程不一致的材料损失[2].另一种方法是使用内聚力单元模拟内界面失效,但是固有型内聚力单元存在人工柔度问题,非固有型内聚力单元需要使用较大的内界面惩罚系数,在模拟复杂断裂问题时存在困难[3-4].扩展有限元法能在有限元模型中显式引入裂纹,是一种受到广泛关注的计算方法,但该方法在引入裂纹时会引入额外的自由度,且通常需要对模型中的裂纹区域进行网格细化和重构,计算效率和稳定性有待进一步提高[5].第二个方面,使用有限元法模拟复杂动态断裂问题时往往会伴随裂纹附近局部区域的网格畸变,由此导致显式动力学求解的临界时间步长显著减小,解的精度下降[6-9].过高的网格畸变甚至会因负体积等问题导致计算终止[9].当前通常的解决办法是在计算过程中删除模型中的畸变,但这同样会导致与物理过程不符的材料损失.
以上所述的传统有限元方法在模拟动态断裂中面临的诸多制约,其根源在于有限元方法使用单元离散求解域,并基于单元节点计算形函数,因此有限元对网格具有很强的依赖性.无网格方法是部分或完全摆脱网格依赖的一类数值方法,其核心思想是采用节点群对结构进行离散,并使用节点描述被离散结构的力学响应[10].因为无网格类方法能有效避免传统有限元法普遍存在的网格畸变问题,因此这类方法一直是国内外计算力学界的研究热点之一.从20世纪90年代起,学者们提出的无网格方法已达20余种,这些无网格法大体上可以分为两种:粒子类方法和基于弱形式的无网格方法.
光滑粒子流体动力学(SPH)方法[11-12]是冲击领域应用较为广泛的一种粒子类无网格法,该方法利用光滑核函数近似模拟场函数,其离散控制方程是配点形式的[13].每个SPH 粒子具有质量、速度、体积等物理属性,这种特性使得SPH 在显式动力学仿真中具有很大优势.但由于SPH 基于配点的强形式,其稳定性难以获得严格的数学证明,因此SPH 往往需要较大的支持域,导致SPH 法的计算量通常高于有限元法[14].物质点法(MPM)是另一种代表性的粒子类方法.MPM 采用欧拉和拉格朗日双重描述将物质离散为一组在空间网格上运动的质点,这些质点同样携带质量、体积、速度等物理信息.动量方程在欧拉描述的空间网格中离散,避免了大变形造成拉格朗日网格畸变的问题[15].文献[16-18]采用物质点法在物体超高速碰撞、冲击侵彻、爆炸、动态断裂等方面开展了一系列研究,取得了重要进展.
Atluti等[19-20]提出的无网格局部彼得罗夫-伽辽金(MLPG)方法和Belytschko等[21-22]提出的无单元伽辽金(EFG)方法是两种较为典型的弱形式无网格方法.这两种无网格法基于弱形式方程,因此具有较好的数值稳定性[19,21,23].然而该类方法的形函数通常为复杂有理函数,这导致了在积分时无法籍由简单的高斯积分直接计算,积分方法不当甚至会影响方法的稳定性.文献[24-26]提出一系列积分方法,在降低计算量、提高积分精度及方法稳定性等方面具有明显效果.
近年来,针对动态载荷作用下的复杂结构破坏问题,国内外学者在近场动力学、边界元、间断伽辽金有限元法等方面也开展了一定工作.刘立胜等采用近场动力学开展了湿热环境下复合材料冲击损伤及动态断裂的研究[27],章青等进行了爆炸载荷作用下混凝土结构破坏过程的近场动力学模拟[28-29],Han等[30]研究了耦合损伤力学与近场动力学的材料失效仿真方法,高效伟等[31]采用边界元法分析功能梯度材料动态断裂力学问题,于福临等开展了基于间断伽辽金方法的船体板架爆炸冲击响应数值模拟研究[32],相关的研究工作仍在进行当中.
综上所述,国内外学者针对动态断裂问题已经开展了多种数值仿真方法的研究,但由于该问题物理过程的复杂性,对动态断裂过程的准确仿真预测仍然是一项具有挑战性的工作.
近年来,作者所在研究团队提出了一种不连续型无网格方法:碎点法(FPM)[33],该方法一方面参考弱形式无网格方法,采用弱形式方程,具有较好的数值稳定性,且基于支持域节点群定义形函数,使子域具有抵抗畸变的能力;另一方面参考间断伽辽金有限元法,不对相邻子域间的位移作连续性要求,因此该方法易于在模型中显式引入裂纹.
碎点法使用空间中的节点群对问题域进行离散,基于节点群划分具有明确几何形状的子域,如图1(a)所示.碎点法模型中仅考虑节点的自由度,子域顶点信息由节点插值获得.节点反映的是相应子域的物理状态,因此节点具有体积、质量、速度等明确的物理含义.对于碎点法模型中的任意一个节点P0及其子域E0,其支持域为子域E0的所有相邻子域E1~E6,则子域E0中的位移形函数是基于支持域节点群P1~P6定义的,如图1(b)所示.由于碎点法使用支持域节点群而非子域顶点构建形函数,计算过程中子域形状的畸变不会对形函数的计算造成影响,因此碎点法具有抵抗子域形状畸变的能力.当然碎点法的支持域定义具有很大的灵活性,可以根据实际计算的需要进行修改,本文仅以图1(b)所示的方法为例进行说明.
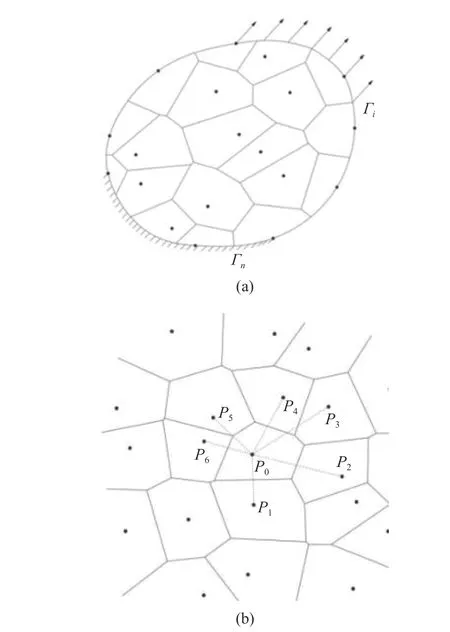
图1 (a) 碎点法模型的离散和(b) 支持域及其节点群的定义Fig.1 (a) Discretization of FPM model and(b) definition of support range and its point cloud
碎点法不对相邻子域间的位移形函数和试函数作连续性要求,即所使用的形函数和试函数可以是分片连续的,如图2 所示.由于只要求函数在子域中局部连续,碎点法可以使用简单多项式形式的位移形函数和试函数,因此子域内的积分计算可以使用简单的高斯积分进行求解,从而避免了大多数弱形式无网格法因需要使用复杂有理数形函数而导致积分困难的问题.另一方面,由于碎点法使用的位移试函数是分片连续的,可以自然地在任意相邻子域之间的内部界面处显式引入裂纹,因此碎点法具备模拟大范围复杂裂纹萌生和扩展问题的能力.在碎点法模型中显式引入裂纹的具体方法将在下文中详细介绍.
图2 (a) 碎点法形函数示意图(b) 位移场为的碎点法位移试函数[34]Fig.2(a) Shapefunctionof FPM(b) FPM’strialfunction of a field of displacement:
碎点法的方程是基于伽辽金弱形式构建的,因此该方法具有较好的数值稳定性.然而,碎点法的位移形函数和试函数是分片连续的,模型中相邻子域间的位移连续性缺乏约束,因此方法的一致性无法得到保证.为了解决这个问题,参考间断伽辽金有限元法,在弱形式方程中任意内界面处引入数值通量修正,以弱形式约束相邻子域的位移连续性.在作者所在团队的前期工作中,已经证明了在弱形式方程中引入内界面数值通量修正可以有效保证碎点法计算的一致性[33].
综上所述,碎点法具有如下优势:(1)采用基于节位移形函数,因此具有抵抗畸变的能力;(2)放弃了相邻子域间的形函数连续性要求,因此可以采用简单多项式形式的位移试函数并用高斯积分求解弱形式方程,且易于在模型中显式引入裂纹;(3)子域具有质量、体积、速度等物理属性,因此便于显式动力学的计算.基于上述特点,作者认为碎点法适合用于预测结构的动态断裂行为.
碎点法已经在多个领域得到了检验和应用.Yang等[34]应用碎点法进行准静态应力分析和断裂分析,验证了碎点法求解上述问题的有效性和准确性;Wang等[35]应用碎点法预测含U 型缺口脆性试件的断裂强度和裂纹形貌,证明碎点法可以有效分析复杂的准静态脆性断裂问题;Guan等[36-37]证明了在分析挠曲电材料的断裂时,碎点法相比于传统有限元法具有计算简单、易于显式引入裂纹的特点;Guan等[38-39]应用碎点法求解非均质材料与复杂薄壁结构的瞬态热传导问题,展示了碎点法在解决复杂问题域及边界的瞬态热传导问题方面的准确性、高效性及稳定性.
本文旨在提出基于碎点法核心思想的动力学碎点法理论并开发相应程序,同时验证该方法分析应力波传播和动态裂纹扩展的有效性.本文的理论推导和算例验证都是基于二维空间小变形假设.本文的结构安排如下:第一章介绍碎点法的基本理论,包括碎点法基本理论、求解域离散方法、弱形式动量方程及其离散、显式动力学求解格式;第二章通过算例验证动力学碎点法在预测应力波传播和动态裂纹扩展方面的能力;第三章对本文做出结论.
1 碎点法基本理论
1.1 求解域离散
碎点法采用布置节点的方式对求解域 Ω 进行离散,在建立碎点法方程时仅考虑节点处的自由度.基于节点进一步将求解域 Ω 划分若干个子域 Ωi,每个子域内部包含一个节点,子域具有明确的几何形状,且相邻子域之间互不相交重叠.碎点法的离散方式如图1(a)所示.
碎点法的离散有两种基本方式,其一是先在求解域中布置节点,然后基于节点定义Voronoi 多边形作为子域,如图1(a)所示.另一种是借助成熟的有限元前处理软件,先在求解域中划分有限元网格,以有限元单元作为碎点法的子域,然后在子域中定义节点.
对于碎点法模型中的任意子域,在子域节点处对其位移函数u进行泰勒级数展开,从而将该子域内的位移函数表示为节点位移和节点位移梯度的函数,由此便定义了子域内的多项式形式的位移试函数,如式(1)所示.以包含节点P0的子域E0为例,在P0处进行泰勒级数展开,则子域E0内的位移试函数如下

节点处的位移梯度可以采用多种方法进行求解,本文所采用的是广义有限差分法.首先定义目标节点P0和子域E0的支持域:本文定义与子域E0相邻且具有公共边界的子域作为支持域,这些子域的节点P1,P2,···,Pm组成支持域节点群,如图1(b) 所示.在定义了子域的支持域之后,可通过广义有限差分法来求解位移梯度.
定义L2范数J如下式所示
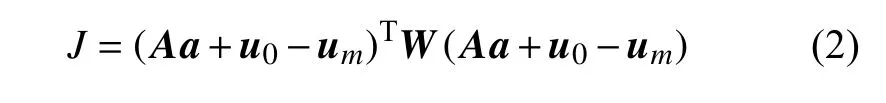
其中a为位移梯度向量,u0和um分别为组装后的P0和P1~Pm节点位移向量,A是包含P0和P1~Pm之间坐标差的张量,W是权函数张量,具体表达式如下
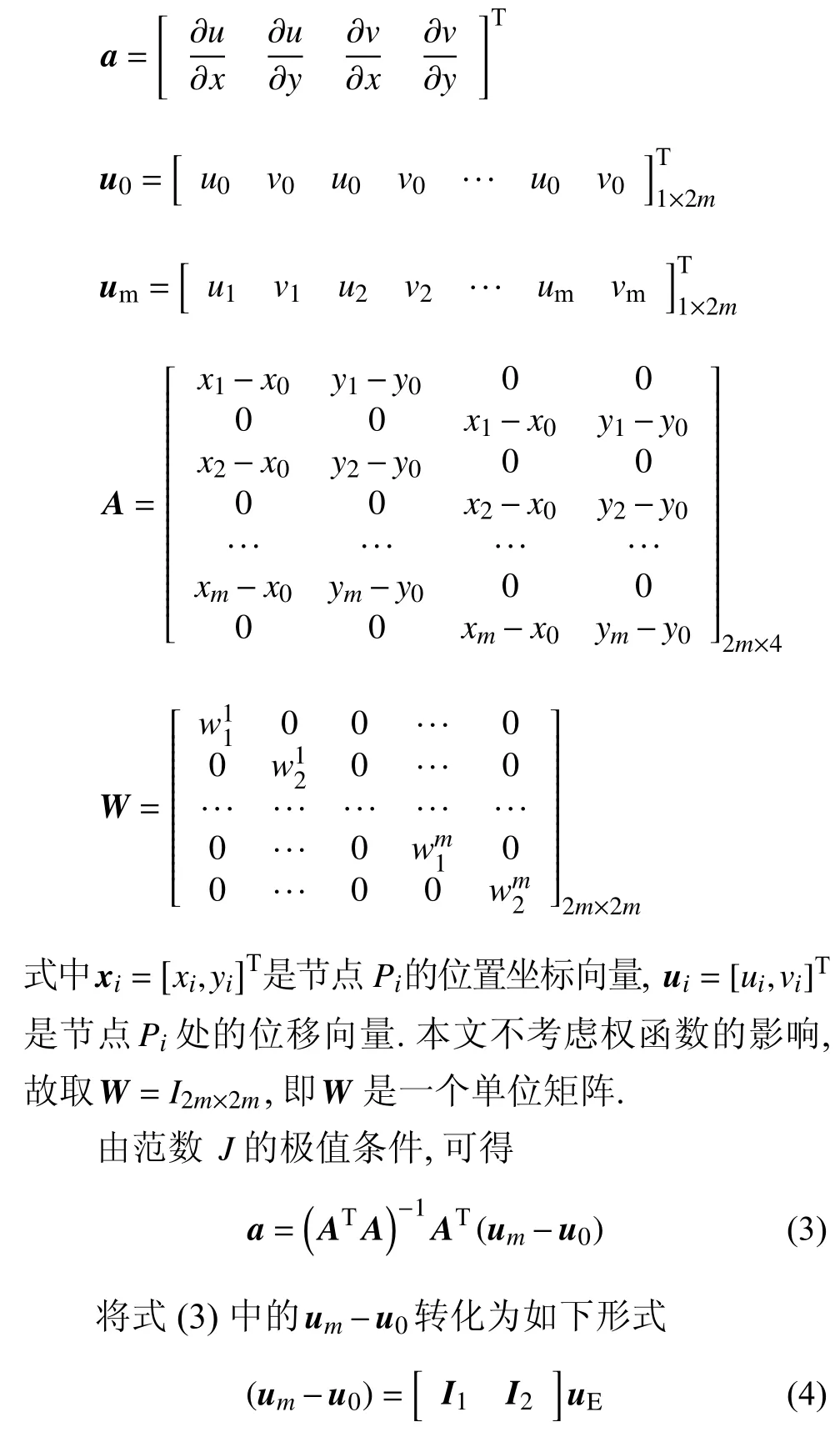
其中,uE为包含P0节点支持域节点群(P0~Pm)位移的组装位移向量,I1和I2为两个转换张量,表达式如下
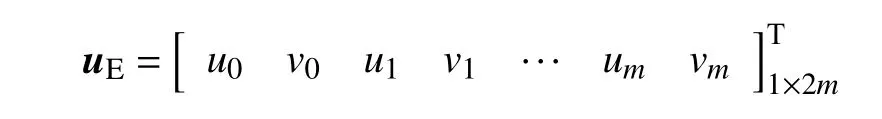

将式(4)代入式(3)可得节点P0处位移梯度向量a与支持域节点群位移向量uE的表达式如下
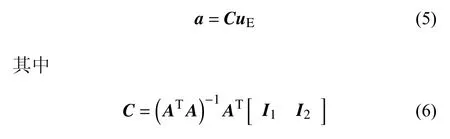
将式(5)代入式(1)中,可以得到子域E0中的位移试函数uh与目标子域的支持域节点群自由度uE之间的关系如下

矩阵N为子域E0内任意一点x=[x,y]T处的位移形函数,其表达式如下

1.2 碎点法的弱形式动量方程
在求解域 Ω 中,强形式动量方程和边界条件为:

式中 ρ为密度,是加速度向量,是施加的体力向量,σij是应力张量.边界条件中的 Γt和Γu分别代表施加应力边界条件和位移边界条件的外边界,ni是边界上的外法线单位向量,和分别为在外边界Γt和Γu上施加的面力和位移.
以虚位移 δui作为检验函数,采用伽辽金法推导弱形式动量方程如下
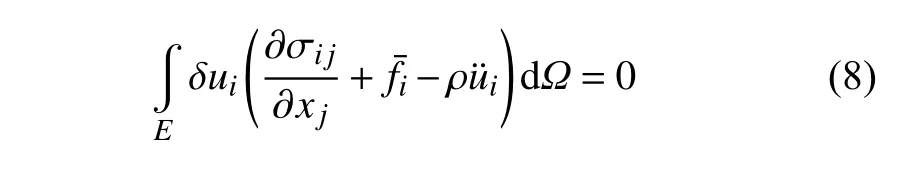
对式(8) 括号内第一项使用分部积分和高斯公式可得
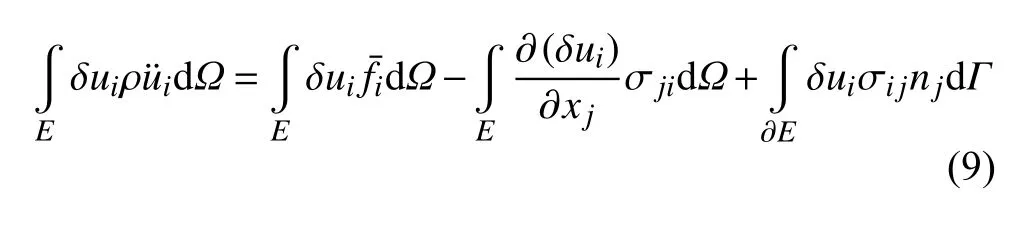
式中 ∂E表示子域E的边界,nj为边界∂E上单位外法向量.
在碎点法模型中,任意子域E都需满足式(9),对所有子域上的方程进行累加可得

定义 Γ 表示所有子域边界的集合,则Γh=ΓΓt-Γu表示所有相邻子域间内边界的集合.假定任意相邻子域E1和E2的公共边界为e,对于任意物理量w,其在边界e上的跳跃算子[]和平均算子{ }定义为

将跳跃算子和平均算子以及面力边界条件引入式(10)的第四项中可得


式中 ηh内边界 Γh处的惩罚系数,用于施加相邻子域间的弱形式位移连续性约束,ηu为外边界 Γu处的惩罚系数,用于施加弱形式位移边界条件,lh和lu分别为 Γh和Γu处子域界面的特征长度.
合并式(14)中等号右边的第三和第四项,并引入内部界面数值通量的定义如下
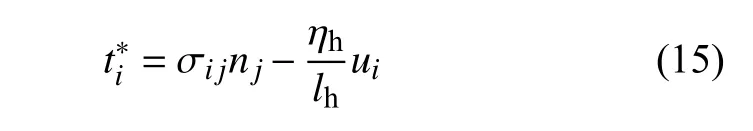
最终推导得到包含数值通量的碎点法弱形式动量方程如下
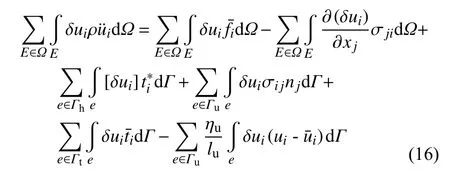
式中等号右边第三项成为数值通量修正项,可以看出在碎点法弱形式方程中,相邻子域之间的相互作用仅由数值通量修正项决定,因此式(15)中定义的数值通量包含相邻子域间相互作用面力的物理含义.
1.3 碎点法弱形式方程的离散
1.3.1 离散格式的弱形式方程离散格式的弱形式方程
为了便于表达,以下推导过程均采用Voigt 标记法的矩阵表达式.
由位移试函数与支持域节点自由度之间的关系式(7)可得速度和加速度的试探函数表达式如下

由于试探解与检验函数采用相同形函数,对虚位移 δu有
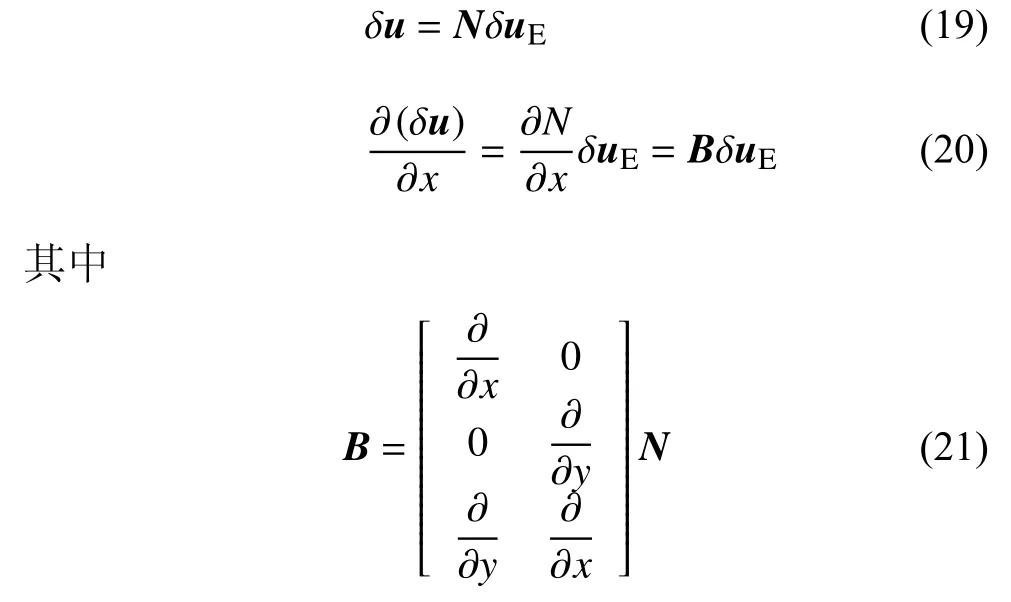
为子域E0的应变形函数.
将式(7)及式(17)~式(20)代入式(16)中,对碎点法求解域中所有子域进行组装,并在等号两边同时消去全局虚位移向量 δuE,可得到离散形式的碎点法动量方程

其中,矩阵M是全局质量矩阵,是全局加速度矩阵,fext是全局等效节点外力矩阵,fint是全局等效节点内力矩阵,其表达式如下
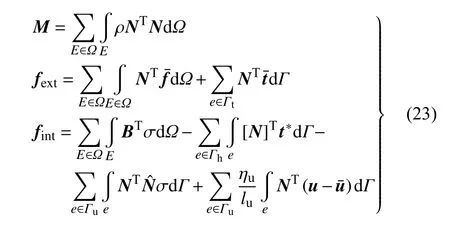
式中,为子域的体力矩阵,为基于应力边界条件施加的面力,为子域的应力,是内边界上的数值通量,是基于内边界单位法向量将子域应力转换成内边界面力的投影矩阵,为子域节点处的位移,为基于位移边界条件施加的位移.
1.3.2 引入裂纹对弱形式方程的处理
碎点法使用的是分片连续的弱形式方程,因此易于在任意内部界面处显式引入裂纹.在离散格式的碎点法弱形式方程式(22)中,任意相邻子域之间的联系包含两个部分,一部分是数值通量上的联系,如上所述,数值通量t*具有相邻子域相互所用面力的物理含义;另一部分是位移形函数上的联系,因为碎点法的形函数是基于支持域节点群计算的,而相邻子域互为对方的支持域.
由于数值通量的物理含义是相邻子域的相互作用面力,可以自然地基于数值通量定义内界面断裂准则.本文使用最大拉应力准则作为断裂准则,即当碎点法模型中任意内界面处的法向数值通量达到材料的拉伸强度时,则判断该内界面发生断裂.当然,本文仅以最大拉应力准则为例,其他断裂准则也可以用作碎点法的内界面断裂判据.
对于碎点法模型中的任意内部边界,当边界的数值通量满足断裂准则时,就在该边界处引入裂纹.如上所述,任意相邻子域之间的联系包括两个部分,因此需分别进行修正.首先,对于断裂的内边界,移除弱形式方程中该边界处的数值通量修正项,即将数值通量置零t*=0,就相当于消除了数值通量部分的相互联系,如图3(b)所示.然后,对该内界面两端子域各自的支持域进行修正,分别从各自的支持域中将对方移除,就相当于消除了形函数部分的相互联系.

图3 碎点法裂纹的引入Fig.3 Steps of introducing crack in FPM
通过以上步骤,就可以在碎点法模型中任意内部边界处引入显式裂纹.值得一提的是,采用上述方法在碎点法模型中引入裂纹时,只修正了裂纹两端子域各自的支持域和移除了该内界面处的数值通量,这些修正只影响裂纹附近局部区域,对整体弱形式方程的影响较小,且不需要进行网格重构,也不会额外增加整体模型的自由度.由此可见,碎点法只需要通过简单的修正就可以在模型中的任意内边界处显式引入裂纹,该操作仅对弱形式方程造成局部影响,且不增加自由度,因此碎点法可以简单、高效地模拟结构中任意位置的裂纹萌生和任意形貌的裂纹扩展,在模拟断裂、破碎等极端问题时具有一定的优势.
1.4 碎点法的显式动力学求解
本文采用中心差分法来对碎点法弱形式动量方程进行求解,中心差分法的时间轴如图4 所示.


图4 中心差分法时间轴示意图Fig.4 Time axis of the Verlet method
将式(24)和式(25)整理可得
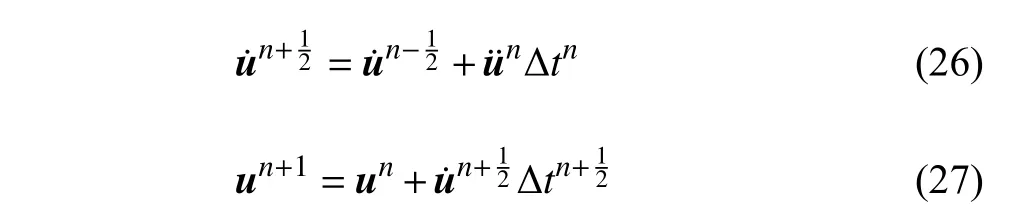
这种形式的中心差分法也通常被称作蛙跳格式.基于该方法,定义动力学碎点法的求解过程如下:
(1) 由式(23)计算tn时刻的质量和节点力矩阵

(7) 重复上述(1)~(6)步,直至最后一个时间步.
由于中心差分法是条件稳定的,因此为了保证计算的稳定性,每一个时间步的时间增量Δt必须小于临界时间步长Δtcr.
下面讨论中心差分法的稳定性问题.为了维持算法的稳定性,时间步长不得超过临界时间步长Δtcr,一般情况下取

式中 α 是安全系数,碎点法参考有限元的安全系数取值,取0.8 ≤α ≤0.98,临界时间步长的计算公式如下

式中le代表碎点法模型中子域的特征长度,c是线弹性材料的绝热声速.
由于碎点法的弱形式方程引入了数值通量修正,用于保证方法的一致性,而数值通量修正项中包含惩罚系数 ηh,如式(15)所示.数值通量会使得整个系统产生一定的数值振荡,而数值通量产生的作用力的大小取决于惩罚系数 ηh,因而惩罚系数会对临界时间步长产生影响,较小的时间步长可以逐渐消除数值通量带来的振荡的影响.
对碎点法中中心差分法的临界时间步长计算公式进行修正得到

使用上式对碎点法模型中的每一个子域进行计算,使用最小的临界时间步长作为整体模型的临界时间步长.
2 碎点法动力学算例
2.1 拉力作用下的平板应力波传播
为了验证动力学碎点法模拟应力波传播的能力,首先应用动力学碎点法程序求解如图5 所示平板的应力波传播问题.参考文献中的设置[40],该算例中使用矩形薄板作为研究对象,矩形板的面内尺寸为长L=4 m,宽D=2 m.平板材料属性为,杨氏模量E=80kPa,泊松比 µ=0,而材料密度 ρ=1 kg/m3.边界条件如图5 所示,矩形板左端固支,右端受均布拉伸载荷P(t),载荷大小随试件的变化关系如图6所示,仿真的总时间设置为0.3 s.由于分析对象为薄板,因此可将该问题等效为平面应力问题,碎点法模型中使用40×20个均匀分布的节点对矩形板进行离散.由于该问题中材料的泊松比设置为零,因此本质上这是一个一维应力波传播问题.

图5 拉力作用下的矩形平板模型Fig.5 The model for rectangular plate under tension
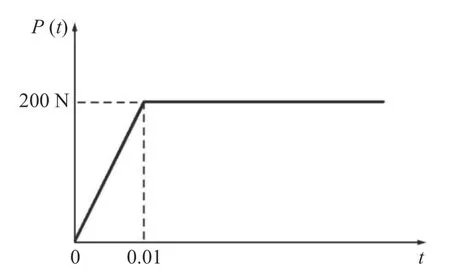
图6 载荷 P(t) 随时间的关系Fig.6 The curve for the load-time correlation
对于此问题,文献[40]给出了自由端A点的水平位移uA、中点B点的水平位移位移uB、中点B点的水平正应力、以及固定端C点的水平正应力的精确解.本文以上述数据为参考对碎点法的计算结果进行验证,同时与有限元结果进行对照.如图7 所示,在碎点法模型中的相同位置读取位移和应力信息,峰值处的相对误差如表1和表2 所示.碎点法的仿真结果与有限元及理论解吻合良好,从而验证了本文所提出的动力学碎点法在模拟一维应力波传播问题方面的有效性.
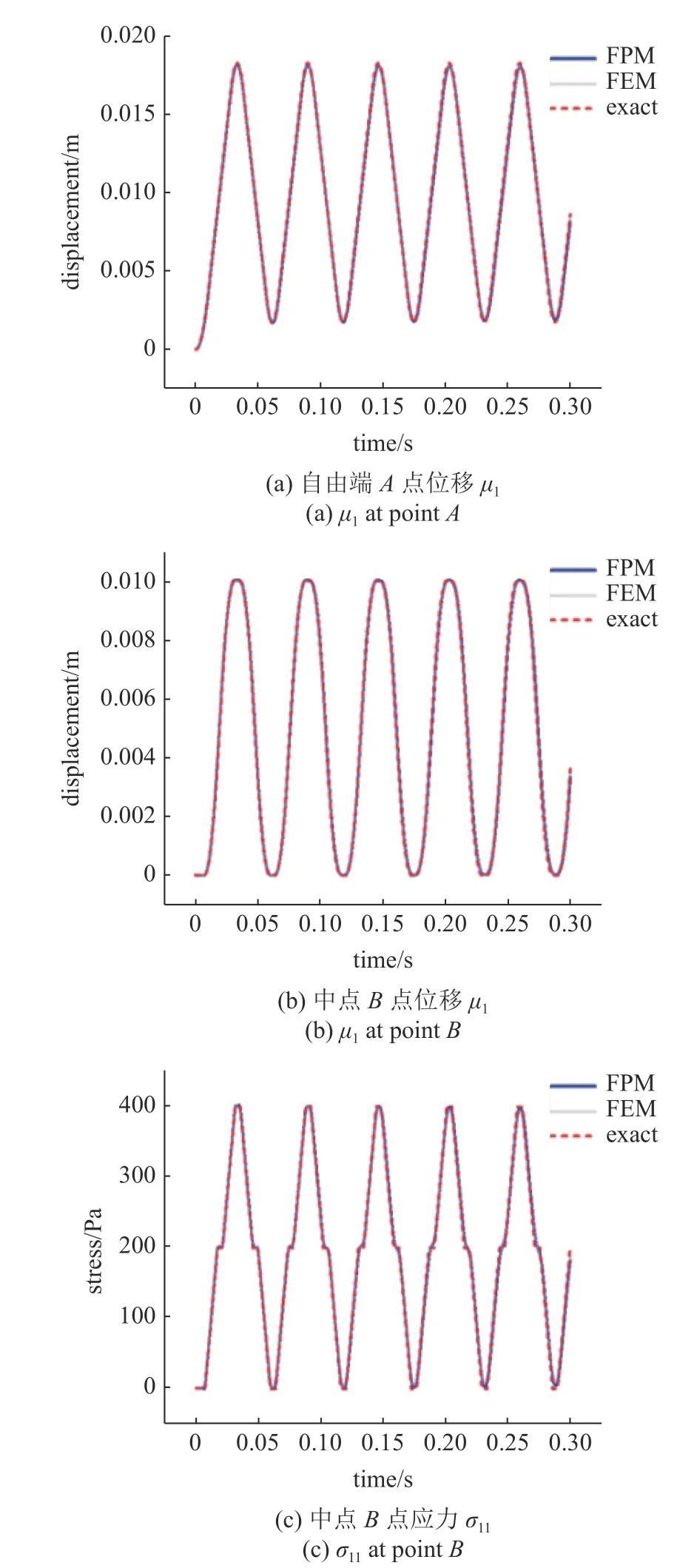
图7 拉力作用下平板应力波传播问题精确解及FPM 结果Fig.7 Exact solutions and FPM’s results of the displacement and stress at different points

图7 拉力作用下平板应力波传播问题精确解及FPM 结果(续)Fig.7 Exact solutions and FPM’s results of the displacement and stress at different points(continued)

表1 有限元、碎点法的位移峰值与理论解的比较Table 1 Relative error of maximum displacement obtained from FEM and FPM

表2 有限元、碎点法的应力峰值与理论解的比较Table 2 Relative error of maximum stress obtained from FEM and FPM
2.2 自由端剪切载荷作用下悬臂梁动态响应
接着使用动力学碎点法程序对自由端剪切载荷作用下的悬臂梁动态响应进行仿真,通过这个算例来验证所提出的方法在模拟二维应力波传播问题方面的能力.该算例中使用图8(a)所示的悬臂梁作为研究对象,梁的尺寸为,长度L=48 m,高度H=12 m.材料的弹性模量E=30MPa,泊松比为0.3,密度ρ=1.0kg/m3.边界条件设置如图8(a)所示,悬臂梁左端面固支,右端面受向下的瞬态剪切载荷P=100Pa,载荷作用时间为0~0.5 s,总仿真时间为 2 s.本算例同样使用平面应力假设,碎点法模型使用 4 8×12 个均匀分布的节点对悬臂梁进行离散,如图8(b).从模型中随机选取一个节点A点,用于读取位移和应力仿真结果.本算例中所设置的几何、材料参数仅用于算法验证,不代表任何具体的物理对象.

图8 (a)悬臂梁示意图和(b)计算模型节点分布Fig.8 (a) Configuration of the beam and(b) the scatter of subdomains
同时,还在商业有限元软件ABAQUS 中建立了这个算例的有限元模型,用有限元模拟结果对碎点法程序进行验证.有限元模型的网格与碎点法模型的子域完全一致.
在图9~ 图11 中分别展示了悬臂梁加载端(右端)中点的竖直位移、固定端(左端)中点各应力分量和A点水平正应力的有限元方法FEM和碎点法计算结果.图11 中仅绘制A点的水平正应力曲线是因为该点处的其他应力分量基本为零.可以看出,碎点法预测的应力和位移状态与有限元结果吻合良好,两种方法得到的应力、位移响应频率特征一致.各图中,两种方法得到的位移曲线几乎完全重合,应力曲线峰值的相对误差在 2.5% 以内,其余部分几乎完全重合.由此可见,本文所提出的动力学碎点法程序可以有效模拟二维应力波传播问题.

图9 自由端中点竖直方向位移响应曲线Fig.9 Vertical displacement curve of the mid-point at the free end of the beam

图10 固定端中点应力响应曲线Fig.10 Curves of stress components of the mid-point at the fixed end of the beam

图11 悬臂梁A 点处应力瞬态响应曲线Fig.11 Stress-time curve of point A
2.3 含裂纹金属板低速冲击破坏行为仿真
最后,使用动力学碎点法程序对一个经典动态断裂问题进行模拟仿真,以验证该方法模拟裂纹动态扩展的能力.该算例基于 Kalthoff等[41-42]在1987 年和2000年所做的一系列试验工作,试验试件如图12(a)所示,为长和宽分别为100mm和200mm的矩形金属板,板上包含着两条对称的水平初始裂纹,裂纹间距为50mm,初始裂纹长度为50mm.试验使用一块底面半径为25 mm 的圆柱形子弹以33 m/s的速度冲击两条裂纹之间的区域[42].试验观察到含裂纹金属板在子弹冲击下的主要失效模式为脆性断裂,裂纹扩展路径与初始裂纹的夹角约为70°,如图12(b)所示.
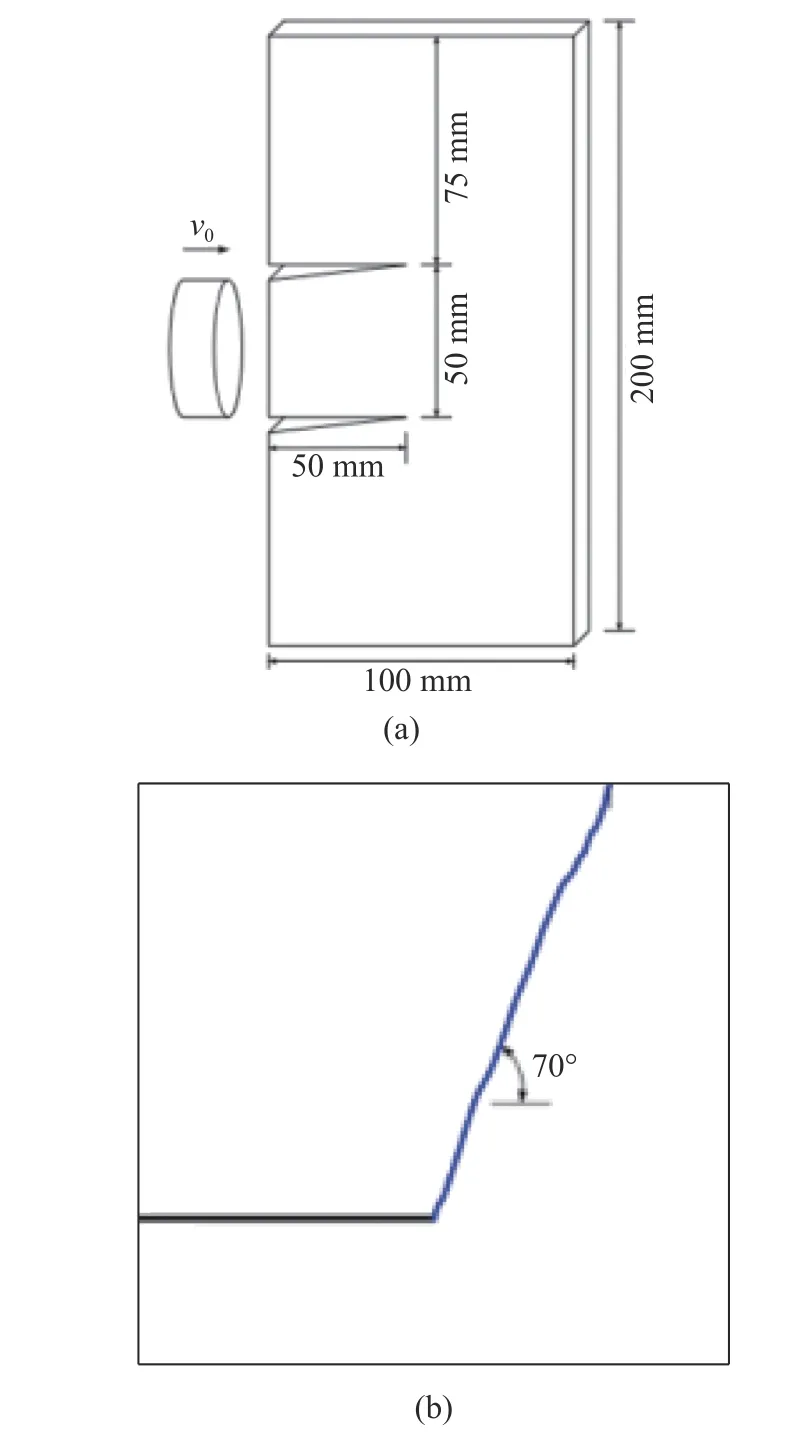
图12 (a)含裂纹金属板冲击试验装置示意图和(b)试验观测到的裂纹扩展路径[43]Fig.12 (a) Experimental setup for the Kalthoff plate impact test and(b) the experimentally-observed crack path[43]
根据该问题的对称性,建立二分之一模型以减少计算量,计算模型如图13(a)所示,图中红色线条代表初始裂纹.文献[33]研究了碎点法节点分布方式给计算结果带来的影响,由于数值通量修正的引入,碎点法使用均匀分布节点或随机分布节点均可以得到准确的结果,验证了碎点法的鲁棒性.基于该特点及试验中观测到的裂纹主要扩展区域,在布置节点时,矩形板右上区域布置的子域节点更加密集,在其他区域子域节点稍微稀疏.这种方式一方面可以更精细地捕捉裂纹的扩展路径,另一方面可以节省计算资源.本文的工作中,邻近子域节点群的选取为所有与该子域共边界的子域节点,并未因节点分布密度不同而进行调整.
试验中金属板由型号18 Ni1900的钢材制成,碎点法仿真中采用文献[44]中的材料参数,杨氏模量E=190GPa,泊松比 µ=0.3,密度 ρ=8 t/m3.根据文献[45],取内界面破坏的拉伸强度为1773 MPa.同时,还建立了使用更加致密节点的碎点法模型,如图13(b)所示,用于分析网格密度对仿真结果的影响,并验证图13(a)所示的有效性.

图13 计算模型:(a) 6516 个子域节点和(b) 11 995 个子域节点Fig.13 Domain discretization with(a) 6516 FPM subdomains and(b)11 995 FPM subdomains
由于冲击载荷作用时间短,可认为子弹速度在冲击过程中几乎没有降低,因此可以在冲击区域用速度边界条件等效代替子弹的冲击载荷.根据文献[45-46],试验中所使用的子弹和试件由相同材料制备而成,二者拥有相同的弹性阻抗,因此加载速度取试验中子弹速度的一半 1 6.5 m/s.
使用碎点法仿真计算得到的静水压力云图如图14 所示,可以看到图14(a)中,在 8 μs 时,由于矩形板左侧载荷的作用,应力波先是沿着矩形板下方初始裂纹与对称面之间的区域,而矩形板其他区域暂时未受到扰动,相应的静水压力均为零.到12 μs时,裂纹尖端处静水压力较大,矩形板其他位置的静水压力几乎为零,如图14(b)所示,这是因为初始裂纹的存在导致了应力波逐渐在初始裂纹尖端处聚集,产生应力集中的现象,仿真的结果与实际的物理机制吻合.
由于裂纹尖端应力集中,裂纹尖端区域的内边界达到强度而开始萌生裂纹,并沿着与初始裂纹夹角约70°角的方向扩展,如图14(c)所示,此时应力集中的位置也随之发生变化,应力集中现象发生在新的裂纹尖端处,而已生成裂纹的区域应力逐渐减小,仿真的结果吻合物理机制.
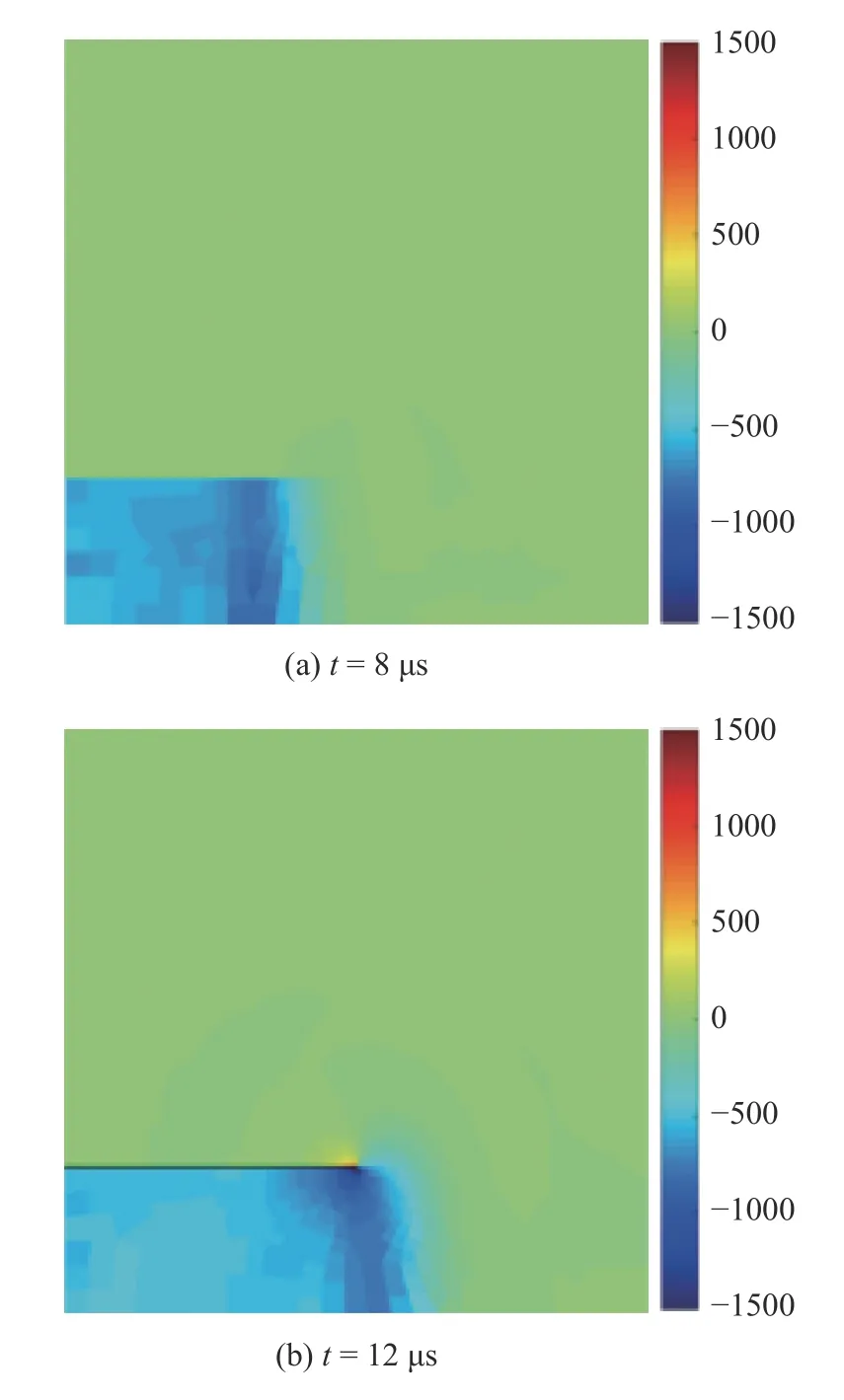
图14 静水压云图Fig.14 Configuration with hydrostatic pressure
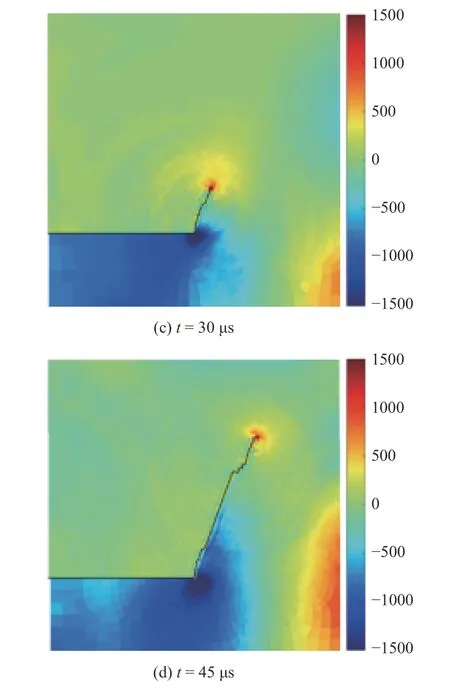
图14 静水压云图(续)Fig.14 Configuration with hydrostatic pressure(continued)
不同节点分布的仿真的裂纹扩展路径在图15中画出.对于仿真结果1,在最初时刻,裂纹以大约70°角开始扩展.随着裂纹扩展到水平位置60mm左右,夹角出现偏转,此时角度约为64°;在水平位置80mm 处左右,裂纹近似沿垂直方向扩展,直至上边缘附近,又重新以约70°角扩展;从初始裂纹尖端到裂纹最终位置的平均角度约为66°.而对于仿真结果2,裂纹几乎一致沿着约70°的角度扩展,仅在接近板上边缘附近出现了角度增大的情况.总体而言,两种不同节点密度的模型预测的裂纹扩展形貌都和试验观测基本一致.其中模型2 使用更致密的节点,因此仿真结果与试验结果吻合更加良好;模型1 的自由度显著少于模型2,计算效率更高,且能够给出关键性的应力传播和裂纹扩展特性,也满足动态裂纹扩展预测和分析的需求.
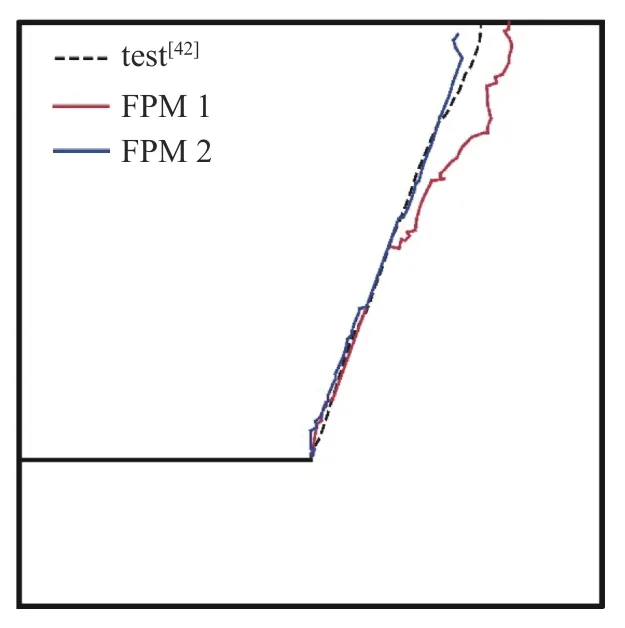
图15 FPM 仿真裂纹扩展路径Fig.15 Crack propagation from FPM simulation
下面绘制裂纹扩展的速度并与文献[45]的仿真结果对比,讨论碎点法仿真得到的裂纹扩展速度的响应特征.根据瑞利波速计算公式

式中cs为剪切波传播速度,可以计算得到瑞利波速为cR=2799 m/s.
对裂纹长度随时间的变化数据进行差分求导处理可求得裂纹扩展速度,如图16 所示,裂纹扩展速度在25 μs 左右时开始增长,之后趋于稳定,在56 μs左右开始出现下降.碎点法得到的裂纹扩展速度略低于文献仿真结果,但总体趋势与文献[45]中数据吻合良好.

图16 裂纹扩展速度-时间曲线Fig.16 Curve of crack propagation speed versus time
以上算例表明,本文所提出的动力学碎点法能够模拟典型的动态裂纹扩展行为,仿真得到的裂纹形貌和裂纹扩展速度与试验观测结果吻合良好.考虑到碎点法可以在任意内界面处判断界面状态,当界面破坏时只需要简单的修正就可以显式引入裂纹,且引入裂纹不会增加模型整体的自由度,因此动力学碎点法具备模拟大规模复杂裂纹萌生和动态扩展问题的能力.
3 结论及展望
本文根据碎点法的基本思想和原理,推导了碎点法弱形式动量方程、建立了显式动力学碎点法求解格式并编制了相应的计算程序,还使用经典算例验证了动力学碎点法模拟应力波传播和动态裂纹扩展问题的能力.
碎点法具有如下特色:(1)碎点法是一种基于伽辽金弱形式的无网格法,具有较好的算法稳定性;(2)采用基于节点的位移形函数,因此具有抵抗子域畸变的能力;(3)碎点法的形函数是分片连续的,因此可以使用多项式形式的形函数,并使用简单的高斯积分进行求解;(4)在弱形式方程中引入数值通量修正项,从而保证放弃了内界面位移连续性的碎点法的一致性和稳定性;(5)内界面数值通量具有相邻子域间相互作用面力的物理含义,因此可用于定义内界面的断裂准则;(6)只需要简单的操作就可以在碎点法模型中显式引入裂纹,即移除对应内界面的数值通量修正,并修改界面两端子域的支持域,从而分别相邻子域间数值通量和形函数两方面的相互联系;(7)子域节点具有质量、体积、速度等明确的物理属性,便于显式动力学计算.
随后通过三个典型算例验证了动力学碎点法对应力波传播及动态裂纹预测的预测能力.前两个算例验证了碎点法模拟拉伸和剪切应力波传播的有效性和准确性,所得结果与精确解和有限元结果吻合良好.第三个算例采用经典动态断裂算例来验证动力学碎点法模拟裂纹动态扩展过程的能力,计算结果与文献中的试验结果吻合良好,体现了碎点法模拟动态断裂的问题的有效性.本文所提出的动力学碎点法理论及程序为动态断裂问题的研究提供了一种简单、高效的数值仿真方法.
最后需要指出的是,本文并未涉及如裂纹分叉、交汇等问题,但碎点法易于显式引入裂纹的特点使得其在这类问题的仿真中具有很大潜力.这些问题背后的复杂物理机制意味着需要做进一步工作,如开发更加细化的界面模型,确定合适的断裂准则,以及建立这些准则与界面数值通量的联系等,这也将是作者团队下一步的研究方向.

