结构爆炸毁伤的浸没多介质有限体积物质点法1)
倪锐晨 孙梓贤 李家盛 张雄
(清华大学航天航空学院,北京 100084)
引言
结构爆炸毁伤现象广泛存在于国防科技、公共安全和国民生产等领域中,例如结构抗爆设计、爆炸事故分析、建筑物定向爆破等.炸药爆炸是典型的多介质流动问题,涉及爆炸产物和传播介质两种物质.爆炸发生后,伴随着剧烈的化学反应和能量转化,爆炸产物急剧膨胀与周围的传播介质相互作用,推动介质产生强烈的压缩进而形成冲击波向外传播.冲击波还会进一步与固体结构相互作用,使结构产生变形和毁伤.实验研究能够反映真实的物理过程,但可重复性差、成本高,通常只能得到一些经验结论或经验公式.由于实际工程结构复杂的几何外形和非线性的材料本构关系,根据特定实验得到的经验结论不具有普遍性.因此,针对这类极端工程问题开发有效且高效的流固耦合算法一直都是热门的研究领域.
根据物质界面的处理方式,多介质流体求解器主要分为两类:精确界面方法(sharp interface method,SIM)和弥散界面方法(diffused interface method,DIM)[1].SIM 需要跟踪和重构物质界面,并在界面处引入额外的控制方程处理密度和内能等热力学量的强间断,包括流场体积分数(volume of fluid,VOF)方法[2-5]和基于水平集函数的虚拟流体方法(ghost fluid method,GFM)[6-8].DIM 将物质界面处理成弥散区域,通过体积分数加权计算相应的热力学量[9-12].与SIM 相比,DIM 全场采用统一的控制方程和数值方法,能够自然地处理新生的物质界面.因此,本文采用DIM 进行多介质流动现象的模拟.
结构毁伤模拟涉及固体结构的极端变形和破坏破碎.拉格朗日方法受限于严重畸变的网格,而欧拉方法则难以记录材料变形历史相关的内变量,都不能很好地模拟建筑物的结构毁伤现象.Harlow[13-14]结合拉格朗日方法和欧拉方法的思想,提出了质点网格(particle-in-cell,PIC)方法,避免了上述网格畸变和内变量记录的数值困难.Sulsky等[15-16]将FLIP PIC方法引入到固体力学领域,提出了物质点法(material point method,MPM)[17-18].近30年来,物质点法在极端变形问题的模拟中表现优异,例如超高速碰撞[19-22]、靶板侵彻[23-24]、断裂裂纹演化[25-26]、流体流动[27-29]以及地质滑坡失效[30-32]等.
浸没边界法(immersed boundary method,IBM)在流固耦合模拟中抛弃了传统的贴体网格,在涉及固体结构大变形及复杂几何外形的问题模拟中表现优异[33].Mittal等[34]根据流固界面处边界条件的施加方式将浸没边界法分为两类:连续力浸没边界法和离散力浸没边界法.其中连续力浸没边界法[35-40]采用罚函数法在描述流固界面的拉格朗日质点上计算流固耦合作用力,并通过离散近似的狄拉克 δ-函数将其弥散到流固界面附近的欧拉网格格心作为控制方程的源项.离散力浸没边界法在流固界面处对流场施加速度边界条件、对固体结构施加力边界条件,根据速度边界条件的施加方式可以进一步分为:虚拟网格方法[41-45]和网格切割方法[46-48].
对于固体结构存在大变形乃至极端变形的流固耦合问题,近年来基于浸没边界法和无网格法的流固耦合算法也得到了初步的应用.Gilmanov等[44-45]将混合浸没边界法(hybrid immersed boundary method,HIBM)与物质点法相结合,针对鱼和浮游桡足类生物在水中的游动现象进行了模拟与研究.张雄等[49]提出了基于拉格朗日乘子的连续力浸没边界法(continuous-forcing immersed boundary method based on Lagrangian multiplier,lg-CFIBM),并将相应的lg-CFIBM-MPM 耦合算法应用于单介质流场中激波与结构的相互作用及结构动态断裂问题的模拟.
本文采用基于黎曼求解器的多介质有限体积法作为流体求解器,采用物质点法作为固体求解器,并将lg-CFIBM 扩展到多介质流体中处理流固耦合边界条件,建立了浸没多介质有限体积物质点法(immersed multi-material finite volume-material point method,iMMFV-MPM)的流固耦合求解器,对近场爆炸下方形钢筋混凝土靶板的失效模式、外爆载荷下建筑物的毁伤现象以及多腔室内爆炸试验进行了模拟,模拟结果与相关实验数据吻合良好,验证了当前建立的流固耦合算法的有效性及精度.
1 流体求解器
1.1 流体控制方程
针对炸药爆炸的模拟,相应的流体控制方程为多组分可压缩欧拉方程

通量G,H的具体表达式与F类似.ρk为流体组分k的密度,αk为流体组分k的体积分数

为流场的单位质量总能量,ek为流体组分k的内能,Yk=αkρk/ρ为流体组分k的质量分数.
为了封闭上述的多组分可压缩欧拉方程,还需要引入各组分的输运方程以及状态方程
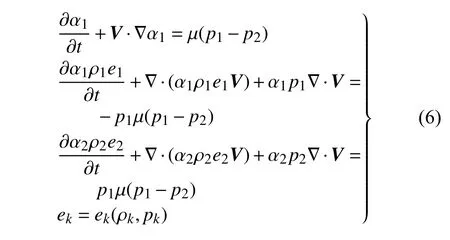
其中V=[u,v,w]为流场x-,y-和z-方向的速度,µ为保证各组分间压强相等的罚函数系数,本文取µ=∞.
1.2 有限体积法黎曼求解器
将守恒形式的微分控制方程(1)改写为有限体积法的积分形式

其中φ(x,y)为坡度限制器[50],本文取

然后,采用HLLC 三波近似求解器[51]计算单元表面Si-1/2,j,k上的黎曼问题

对于非守恒形式的输运方程(6),采用算子分裂方法进行计算:首先,允许各组分间的压强存在差异进行输运计算;然后,通过压力松弛调整各组分的体积分数保证各组分间的压强相同.输运部分的控制方程为

上述3 个方程均由3 部分组成:时间偏导数项、守恒形式的通量项以及非守恒形式的速度散度项.因此以体积分数为例,结合式(10)给出的界面黎曼状态,输运方程的半离散形式为

对于半离散形式的式(7)和式(13),均采用具备TVD性质的3 阶龙格库塔格式进行时间积分.
1.3 压力松弛
压力松弛过程需要保证单元内部的质量、动量和能量守恒,通过调整各组分的体积分数、密度和内能使得各组分的压强相等.具体的控制方程为
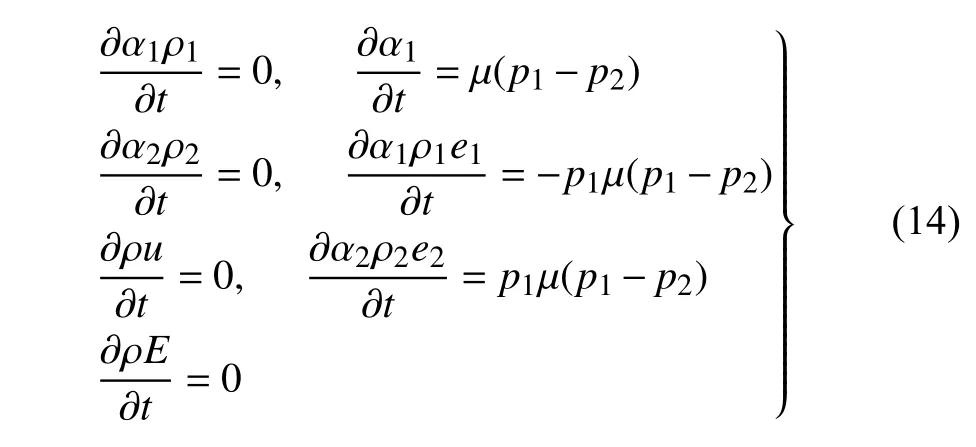
通过推导化简[1]可以得到最终的松弛方程为

2 固体求解器
2.1 固体控制方程
更新拉格朗日格式下质量、动量和能量的守恒方程为
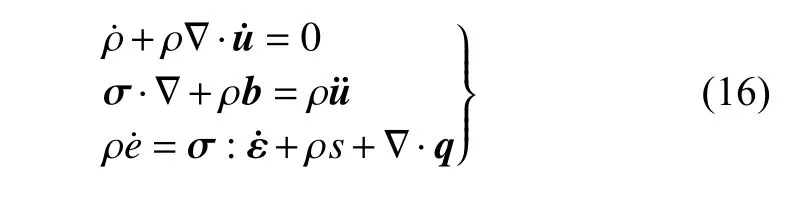
其中 ρ 表示当前时刻的密度,u表示位移,σ 表示当前构型下的柯西应力,b表示单位质量的体力,ε 表示应变张量,s表示单位质量的热源,q表示单位时间下单位面积的热流密度.
大部分的固体材料本构描述的是应变率张量和应力率张量之间的关系

其中 σ∇为柯西应力张量的焦曼率导数.
为使式(16)定解,相应的动力学条件和初/边值条件为

2.2 物质点法

如图1 所示,物质点法将物质区域 Ω 离散为一组拉格朗日质点,因此连续体密度可以近似为

图1 物质点法的空间离散Fig.1 Spatial discretization of MPM

其中np表示质点总数,mp表示质点p的质量,xp表示质点p的位置坐标,δ表示狄拉克函数.
物质点法在每个时间步中的拉格朗日步进行动量方程的求解,质点和网格保持相对位置固定,因此可以采用有限单元法中的形函数NI(x) 插值得到计算域的位移场

其中uI是网格节点的位移,ng是背景网格节点数量.
将式(20)和式(21)代入式(19)中,可以得到定义在背景网格节点上的离散动量方程

分别是网格节点I处的内力和外力,NIp=NI(xp)是质点p处的形函数,σp=σ(xp) 是质点p的应力,h是为了将弱形式(19)中最后一项面积分转换为体积分而引入的假想边界层厚度.
显式物质点法采用中心差分法的蛙跳格式进行动量方程的时间步推进

2.3 物质点法格式
在显式物质点法中,物质点上的应力状态更新既可以在每个时间步开始时进行,也可以在每个时间步结束时进行,分别称为USF(update-stressfirst)格式和USL(update-stress-last)格式[18].在改进的USL(modified USL,MUSL)格式中,将更新后的质点动量映射回网格节点,并采用该节点速度场进行质点应力状态的更新.
Ni等[52]指出拉格朗日属性的质点位置和欧拉属性的网格间相互作用都会影响物质点法的稳定性,并且证明了USL 格式的本质不稳定性.Bardenhagen[53]发现MUSL 格式在模拟过程中总能量会缓慢耗散,而USF 格式的总能量则会逐渐增加.相应的数值黏性使得MUSL 格式相比于USF 格式更稳定.因此,本文将采用MUSL 格式的物质点法.
3 流固耦合算法
3.1 网格单元分类
为了施加流固边界条件,需要先定位浸没边界的位置.如图2 所示,处于固体结构内部的网格单元被分类为type I,处于流场内部的网格单元被分类为type II,而被浸没边界穿过的网格单元被分类为type III.

图2 网格单元分类Fig.2 Grid cell classification
固体结构的运动由拉格朗日属性的物质点进行跟踪,而图2 中红线所示的浸没边界仅用于说明,在实际模拟过程中并不会显式重构边界.因为当固体结构发生破碎后,通过三维空间内的点云跟踪并重构新生的浸没边界过于复杂、不稳定并且耗时.可以从浸没边界的定义出发

其中 Ωp是质点p占据的区域,通过物质点的分布来确定网格单元的分类.具体步骤如下.
(1) 识别每个物质点位于哪个网格单元内,并初步将网格单元分为两类:物质点单元和空单元.空单元即为流体网格单元(type II).
(2) 搜索每个物质点单元的相邻单元.若所有相邻单元均为物质点单元,则该物质点单元为固体网格单元(type I);否则,该物质点单元为流固两相网格单元(type III).
3.2 基于拉格朗日乘子的连续力浸没边界法
如图3 所示,传统的连续力浸没边界法通过罚函数法实现,无法在每个时间步严格满足滑移或无滑移边界条件,因此无法捕捉与边界速度方向密切相关的激波结构,例如马赫反射.传统的离散力浸没边界法在每个时间步都需要计算流固耦合界面的法向和垂直距离,计算效率较低.并且在爆轰波驱动下结构动态断裂问题的模拟中,固体结构会产生尺寸不足一个网格的细小碎片,还会产生大量的新生流固耦合界面,这些都使得流固界面难以追踪并重构.因此,本文将Ni等[49]提出的基于拉格朗日乘子的连续力浸没边界法(lg-CFIBM)扩展到多介质流体中.该算法在每个时间步内严格满足速度边界条件的同时,不再需要重构流固耦合界面,适用于结构爆炸毁伤问题的模拟.

图3 各浸没边界法边界条件施加示意图Fig.3 Diagram of applying boundary conditions of different IBMs
根据式(23)和式(24)重构得到的背景网格节点动量和集中质量,固体结构在type III 单元格心处的速度场可以由下式给出

其中nen是每个单元的节点数量.通过将type III 单元格心处的流场速度vc设置为浸没边界的外插速度,浸没边界上的速度边界条件就可以在每个时间步严格满足.
式(29) 速度边界条件的施加方式等价于在每个type III 单元格心处施加相应的欧拉源项

其中k表示龙格库塔循环的阶次,.在lg-CFIBM 中,type III 单元只记录单元表面的数值通量,因此根据全微分公式Δ(ρv)=ρΔv+vΔρ,式(30)可以改写为

根据动量守恒定律,式(31)欧拉源项的反作用力需要施加到固体结构上


另外,type III 单元还扮演着在物质点法中计算流固耦合表面应力的角色.通过将式(26) 中的替换为Fp,物质点法中的节点外力公式可以化简为

4 数值验证
为验证所建立的流固耦合算法的数值精度和有效性,本文分别模拟了二维激波与氦气泡相互作用、近场爆炸下方形钢筋混凝土靶板的失效模式、外爆载荷下建筑物的毁伤现象以及多腔室内爆炸试验4 个算例,并将模拟结果与相关实验结果进行了对比.
4.1 二维激波与氦气泡相互作用
为了验证所建立的多介质有限体积黎曼求解器具备描述多介质流动及激波捕捉的能力,本小节模拟了经典的标准算例“二维激波与氦气泡相互作用问题”[54].
激波前后的流场状态应满足激波间断关系

其中MS为入射激波的马赫数.激波前空气区域的无量纲参数设置为

则激波后空气区域的无量纲参数可以由式(35)和MS=1.22计算得到

氦气泡区域相应的无量纲参数为

空气和氦气的力学行为均由理想气体状态方程
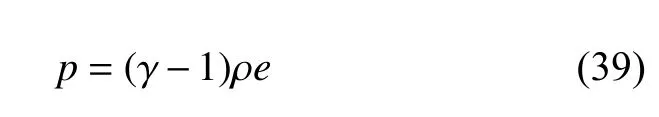
进行描述,相应的气体常数分别为 γ1=1.4(空气)和γ2=1.67(氦气).
如图4 所示,整个计算域[0,325]×[-44.5,44.5]采用单元尺寸为h=0.25 的均匀网格进行空间离散.x=325处为入流边界条件,并以式(37)描述相应的入流流场状态;x=0处为出流边界条件;其余边界均为对称边界条件.直径D=50的氦气泡的圆心位于(x=175,y=0) 处,而入射激波的初始间断面位于x=225处.各个时刻的计算模拟结果与实验数据的对比如图5 所示.文献[54]给出了氦气泡表面的激波演化示意图,如图6 所示.

图4 二维激波与氦气泡相互作用问题描述Fig.4 Diagram of 2D shock-helium bubble problem
从图5(a)和图6 的对比中可以看到当前的多介质有限体积算法(MMFVM)可以很好地捕捉氦气泡表面的激波演化,包括入射激波、折射激波、反射激波、侧面激波和膨胀扇区.同时,从图5 各个时刻计算模拟的纹影图结果和实验照片的对比中可以看出,MMFVM能够很好地模拟多介质的流动现象并捕捉相应的物质界面形状.

图5 二维激波与氦气泡相互作用问题的模拟结果(左)和实验结果[54](右)Fig.5 Numerical results(left) and experiment data[54](right) of 2D shock-helium bubble problem

图6 氦气泡表面的双反射-折射示意图[54]Fig.6 Schematic for twin regular reflection-refraction[54]
4.2 近场爆炸下方形钢筋混凝土靶板的失效模式
如图7 所示,Wang等[55]针对近场爆炸下方形钢筋混凝土靶板的失效模式进行了实验研究.本小节将分别采用iMMFV-MPM 算法和MPM 算法对该问题进行计算模拟,从而证明iMMFV-MPM 算法相比于MPM 算法的优势.

图7 实验装置及钢筋混凝土的布筋形式[55]Fig.7 Geometry setup of experiments[55]
如图8 所示,根据问题的对称性,采用 1 /4 模型进行计算模拟.计算域尺寸L=W=H=600mm,采用单元尺寸h=8 mm 的均匀网格进行离散.尺寸为550mm×500mm×40mm 的靶板距离爆炸中心R=400mm,采用体积为2 mm×2 mm×2 mm 的物质点进行离散.质量为m=0.46 kg 的球形炸药设置于计算域原点处.x=0mm,y=0mm和z=0mm 处为对称边界条件,其余边界处均为出流边界条件.

图8 计算模拟的几何参数设置Fig.8 Geometry set for simulation
TNT 炸药采用JWL 状态方程进行描述[55]

其中V=ρ/ρ0为相对体积,炸药的初始密度为ρ0=1.63 mg/mm3,E为单位初始体积的内能,相应的初始值为E0=7000mJ/mm3,其余参数设置为A=371.2 GPa,B=3.21 GPa,R1=4.15,R2=0.95,w=0.3.
混凝土是水泥作为胶凝材料,砂石作为集料,通过与一定比例的水搅拌而成的材料.目前常用的混凝土材料本构为Holmquist-Johnson-Cook(HJC)本构[56],其将混凝土大变形过程中的孔洞坍缩所产生的效应引入了强度模型中,能够很好地描述混凝土材料在高应变率、高应力下的大变形和破坏行为.在本算例中,混凝土的密度为 ρs=2.44 g/cm3,杨氏模量为E=35.66 GPa,泊松比为 ν=0.2,其余参数如表1和表2 所示.

表1 钢筋混凝土靶板算例中HJC 强度模型参数[56]Table 1 The material constants of HJC strength model in reinforced concrete slab simulation[56]

表2 钢筋混凝土靶板算例中HJC 状态方程参数[56]Table 2 The material constants of HJC EOS model in reinforced concrete slab simulation[56]
钢筋的力学行为采用简化Johnson-Cook 模型进行描述[55]

iMMFV-MPM 算法和MPM 算法模拟得到的几个典型时刻的压力云图如图9 所示.iMMFV-MPM能够很好地捕捉爆轰波的传播和反射现象,保持尖锐的激波面.并且在t=0.18ms 时刻,钢筋混凝土靶板背面出现拉伸失效区域,从而引发层裂现象.然而在MPM 的模拟过程中,由于跨网格噪声和数值断裂,激波面无法维持完整的球面,并且在激波面附近产生大量速度过高的质点,导致t=0.08 ms 时刻爆轰波就与钢筋混凝土靶板产生相互作用.这些散乱的高速质点撞击到钢筋混凝土靶板上,产生大量零散的、非物理的高应力区,导致无法观测到相应的层裂现象,如图9(d)所示.
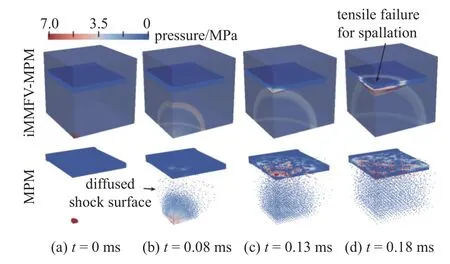
图9 iMMFV-MPM和MPM 的压力云图结果Fig.9 Pressure contour results of the iMMFV-MPM and the pure MPM
钢筋混凝土靶板上的失效云图及失效模式如图10所示,并且在后处理显示中将钢筋网格人为移动到靶板表面用于定位裂纹和层裂区域的位置.从图10(a)中可以看出,靶板呈现中等程度的损伤并且在背面出现明显的层裂剥落.层裂剥落区域的平均半径为 1 20mm,层裂深度为靶板厚度的一半,正好暴露出钢筋网络[55].靶板背面存在一系列从层裂区域出发的主裂纹,其中水平和竖直方向上的3 条主裂纹均沿着钢筋网络分布.从图10(a)和图10(b)的对比中可以发现,iMMFV-MPM 模拟捕捉到的失效模式与实验结果吻合良好.相应的层裂剥落区域平均半径约为 1 12 mm,略小于实验结果,并且在夹支方向上(横向)剥落区域的尺寸略大于非夹支方向(纵向),与实验结果一致.同时从y=25 mm 的截面失效云图结果中可以发现,层裂现象终止于靶板厚度方向的中部.然而,在MPM 模拟结果中,整个钢筋混凝土靶板几乎完全失效,无法观测到相应的层裂现象,如图10(c)所示.

图10 方形钢筋混凝土靶板的失效模式Fig.10 Damage modes of the reinforced concrete slab
iMMFV-MPM 模拟的钢筋混凝土靶板中心点的时程位移曲线如图11 所示,而MPM 的模拟结果由于靶板中心损伤过于严重而无法给出相应的中心点位移曲线.Wang等[55]在实验中测量得到靶板中心点的最大位移为 3 5 mm,而iMMFV-MPM 的模拟结果为 3 5.9 mm,与实验结果的相对误差为 2.6%,吻合良好.

图11 iMMFV-MPM 模拟的钢筋混凝土靶板中心点位移时程曲线Fig.11 Central deflection curve of the reinforced concrete slab by iMMFV-MPM
4.3 外爆载荷下建筑物的毁伤现象
如图12(a)所示,Baylot等[57-58]对外爆载荷作用下建筑物的毁伤现象进行了实验研究.基于问题的对称性,本文建立了如图12(b)所示的几何模型,具体的几何尺寸及钢筋的布筋方式参照文献[57].

图12 实验装置及计算模拟的几何建模Fig.12 Setup of experiment and simulation
实验中采用 7.1 kg 的C4 炸药,等价于8.449 kg的TNT 炸药,TNT 炸药的相关参数设置与式(40)相同.混凝土的力学行为采用HJC 模型[58]进行描述,密度 ρ=2.068 g/cm3,杨氏模量E=28.7 GPa,泊松比 ν=0.19,抗压强度=42 MPa,其余的HJC 模型参数与表1和表2 相同.钢筋的力学行为采用线性强化弹塑性模型进行描述,密度 ρ=7.5 g/cm3,杨氏模量E=200GPa,泊松比 ν=0.3,屈服强度 σy=449 MPa,极限强度 σb=513 MPa,失效应变 εf=0.18.
模拟得到的几个典型时刻的流场压强云图和建筑物损伤云图如图13 所示,z=300mm 平面上的流场体积分数云图和建筑物的压强云图如图14 所示.炸药爆炸形成球形的爆轰波,在t=0.5 ms 时爆轰波与下层中心柱相互作用形成高压的反射波如图13(a)所示,下层中心柱迎爆面上的混凝土材料在高压爆轰波的作用下孔隙被逐渐压实、损伤度逐渐累积如图13(b)所示.流场经过立柱和中板还会出现明显的绕流现象,如图13(b)和图14(a)所示.在高压反射波的驱动下,中心立柱附近的爆炸产物出现了明显的回卷现象,如图14 的体积分数云图所示.由于中板下方的流场压强明显高于上方的流场压强,中板会向上隆起,表现为中板上表面主要分布拉应力,如图14所示.在本实验中,Baylot等[57-58]将钢筋配置在混凝土内部接近表面处,因此计算模拟结果中混凝土结构上没有出现层裂现象.而下层中心柱背爆面中部的损伤度累积则是由大变形的钢筋挤压混凝土引起的.下层中心柱弯曲后上下两端连接处受到强剪切作用,导致出现强烈的毁伤现象如图13(d)所示.

图13 流场压强云图与建筑物损伤云图Fig.13 Pressure contour in fluid domain and damage contour in building
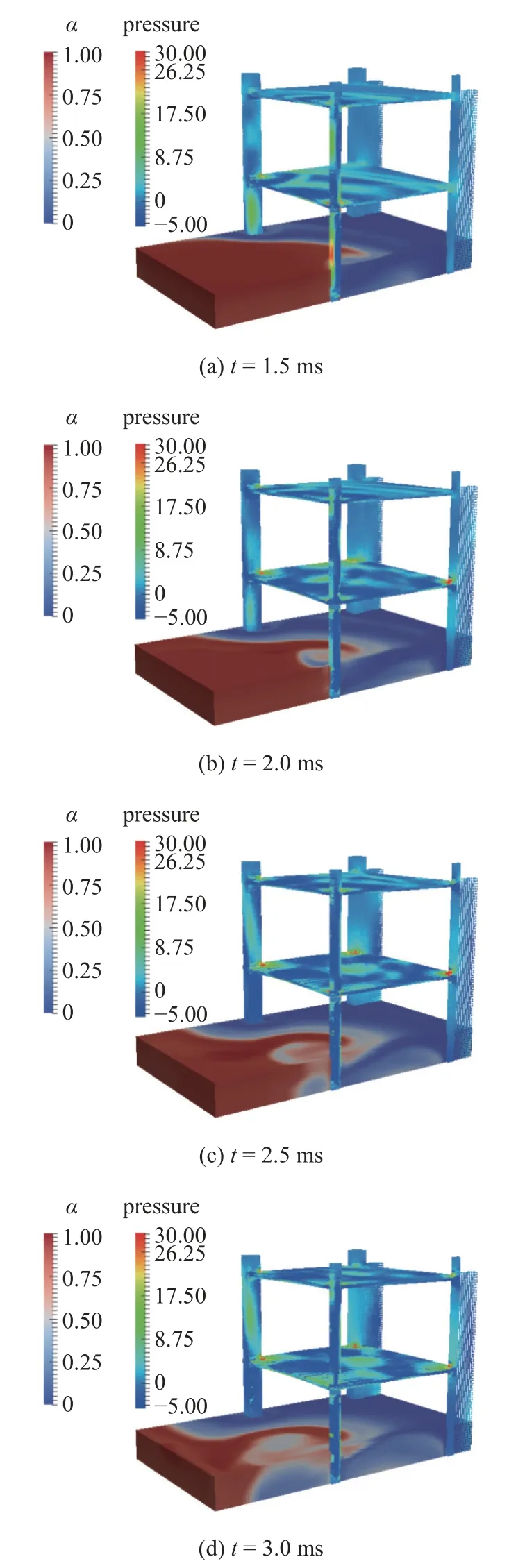
图14 流场体积分数截面云图与建筑物压力云图Fig.14 Volume of fraction contour on the plane of z=300mm and pressure contour in building
爆炸结束后建筑物毁伤的实验结果和计算模拟结果如图15 所示.计算模拟的建筑物毁伤现象与实验结果吻合良好,下层中心柱的上下两端连接处均出现了剧烈的损伤,中板的上表面都能观测到相应的裂纹分布.从侧面损伤度云图和实验侧面照片的对比中可以看出,中板均存在明显的隆起,并且中部存在一条贯穿裂纹.

图15 最终时刻的建筑物损伤云图Fig.15 Damage contour in building at last
4.4 多腔室内爆炸试验
郭志昆等[59]对扁平箱形密闭结构内爆炸问题进行了实验研究,具体的几何参数设置如图16(a)所示.本文建立了如图16(b)所示的几何模型(未显示顶板)进行计算模拟.

图16 实验和模拟的几何参数设置Fig.16 Geometry setup of experiment and simualtion
实验中采用 2 20g 的TNT 炸药,TNT 炸药的相关参数设置与式(40)相同.实验采用的混凝土设计强度等级为C30,相关HJC 模型的材料参数来自文献[60],密度 ρ=2.4 g/cm3,泊松比 ν=0.202,杨氏模量E=33.4 GPa,抗压强度=39.2 MPa,最大静水拉力T=3.162 MPa,其余参数与表1和表2 相同.实验采用的钢筋为HPB235 级钢筋,其力学行为采用理想弹塑性模型进行描述,密度 ρ=7.8 g/cm3,杨氏模量E=220GPa,泊松比 ν=0.3,屈服强度 σy=235 MPa.
主爆室外侧墙中心点处的压强时程曲线如图17 所示,爆轰波作用在侧墙中心点处的超压峰值为0.938 MPa,实验中相应测点处测得的超压峰值为0.987 MPa,相对误差为4.96%,与实验结果吻合良好.几个典型时刻中截面上的流场压强云图和体积分数云图如图18 所示.方形炸药包爆炸后,爆炸产物急剧膨胀并推动周围空气产生爆轰波如图18(a)所示,在t=1.5 ms 时,爆轰波与主爆室的侧墙相互作用产生反射波,形成图17 中的第1 个超压峰值(peak 1).t=3.5 ms 时,顶板与底板的反射波在中截面处相交形成二次反射波如图18(b)所示,该二次反射波与主爆室的侧墙相互作用,形成图17 中的第2 个超压峰值(peak 2).相邻侧墙上的爆轰反射波传播到外侧墙中心点处形成第3 个超压峰值(peak 3);顶板与底板的二次反射波在相邻侧墙上反射后传播到外侧墙中心点处形成第4 个超压峰值(peak 4);正对侧墙上的爆轰反射波传播到外侧墙中心点处形成第5 个超压峰值(peak 5).
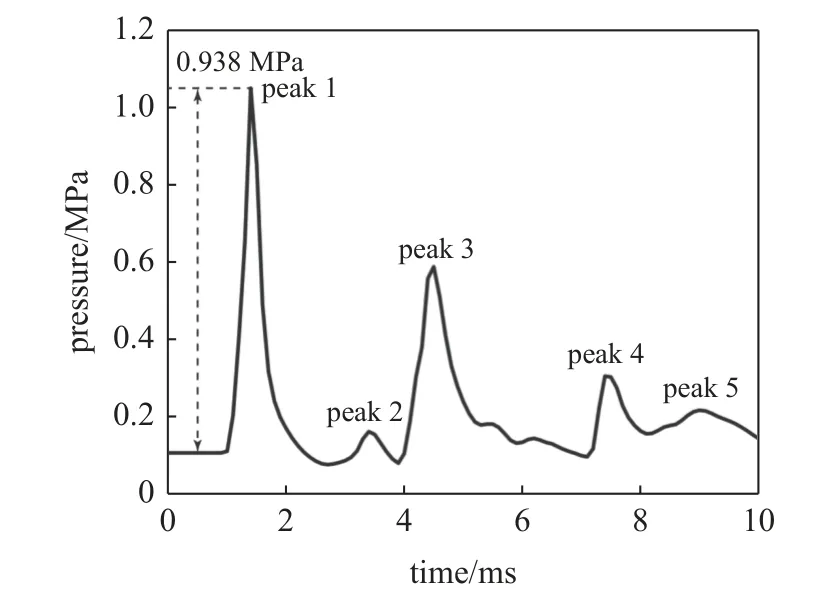
图17 主爆室侧墙中心点处的压强曲线Fig.17 Pressure curve at the center of sidewall in explosion room

图18 各时刻中截面上的流场压强云图和体积分数云图Fig.18 Pressure contour and volume of fraction contour of middle plane at different instants
从图18 各时刻的压强云图和压强标尺中可以发现,主爆室的超压峰值在1 MPa 左右,而侧爆室的超压峰值骤降为0.05 MPa~0.1 MPa,对角爆室的超压峰值则为0.02 MPa 左右,这与实验观测到的各爆室的超压峰值比例一致.从各时刻的体积分数云图中可以发现,爆炸产物基本都残留在主爆室内,主/侧爆室之间的内墙开窗方向上形成对外的高压射流,而在4 个角区方向上形成“蘑菇伞”状的物质界面结构.
最终时刻顶板和主爆室侧墙的破坏情况如图19所示.从图19(b)中可以看出,由于非爆室的超压峰值骤降为主爆室的1/10甚至更低,破坏都集中在主爆室,而非爆室墙体仍处于弹性工作状态,与实验观测结果一致.主爆室的顶板中心区域发生剧烈的贯穿破坏,其位置和大小与实验照片基本一致;并且大量的非贯穿裂纹从中心贯穿区域边缘向四周延伸.从图19(b)最右侧的侧墙破坏情况中可以发现,结构内转角处是薄弱部位,出现了明显的通长裂纹,这与实验观测结果一致.

图19 顶板和侧墙的破坏情况Fig.19 Roof and sidewall fragmentation
5 结论
本文针对建筑物爆炸毁伤的流固耦合问题,通过基于拉格朗日乘子的连续力浸没边界法(lg-CFIBM)将多介质有限体积法(MMFVM)和物质点法(MPM)相结合,建立了浸没多介质有限体积物质点耦合算法(iMMFV-MPM).首先通过二维氦气泡与激波相互作用的典型算例验证了上述算法具备求解多介质流动及激波捕捉的能力.在此基础上,对近场爆炸下方形钢筋混凝土靶板的失效模式、外爆载荷下建筑物的毁伤现象以及多腔室内爆炸试验进行了模拟,得到以下结论.
(1) 相比于传统的采用纯MPM 模拟流固耦合问题,建立的iMMFV-MPM 方法在模拟炸药爆炸产生爆轰波的过程中可以得到更锐利的波阵面,从而在后续爆轰波与固体结构相互作用以及固体结构毁伤现象的模拟中得到高精度的结果.
(2) 将基于单介质流体的lg-CFIBM 流固耦合算法扩展到多介质流体中,能够较好地模拟近场爆炸下爆炸产物与固体结构间的相互作用,例如大楼外爆炸算例中,中心立柱附近爆炸产物的绕流和回卷现象.
(3) 采用iMMFV-MPM 方法首先对建筑物中最常见的钢筋混凝土结构进行了近场爆炸下失效模式的模拟,能够很好地捕捉到层裂现象;此外,根据爆炸载荷常见的两种形式分别模拟了“外爆炸载荷下建筑物的毁伤现象”和“多腔室内爆炸试验”,给出了爆炸产物和空气的流场演化以及结构的变形和毁伤特性分析,均与相应的实验结果吻合良好.

