非均质边坡稳定性计算方法的差异化研究

郑家昌，董军，秦颖，贾烊

（1.北京建筑大学工程结构与新材料北京市高等学校工程研究中心，北京 100044；2.中国建筑国际工程公司，北京 100029）

1 引言

随着国家“一带一路”倡议的全面推进，我国对外工程数量整体呈现增长态势。“一带一路”倡议在将我国基础设施建设的优势带向世界的同时，也给工程项目带来了相关标准、规范的国内外差异等问题，导致我国外派项目在项目设计、施工等方面与当地监理、建设方在沟通中存在分歧。对此，国内众多学者作了一定程度的努力。例如，陈国良[1]等对中东地区某抽蓄工程土石坝边坡稳定抗震设计进行了研究，并对美国垦务局的相关规范、计算方法等进行了梳理，与中国标准的计算成果进行了对比。祝振兴[2]对钢筋混凝土的设计与计算方法进行了研究，并与中国规范、美国规范、欧洲规范进行了详细的对比分析。

现如今，国内外学者对均质边坡的研究较多，相关计算、分析方法较为成熟[3-5]。但是对非均质边坡的稳定性分析较少。其中，王俊杰等[6]研究了非均质土坡失稳的判断依据，分析了非均质土坡失稳破坏的过程，提出了以特征点位移矢量突变结合塑性区贯通的失稳来进行土坡稳定的综合判据方法。李小春等[7]基于某隧道边坡，进行了多滑裂面的边坡稳定性分析。马伟[8]对非均质边坡进行了有限元分析，研究了单元类型的不同对土坡稳定性分析的影响。

本文结合我国外派玻利维亚的某工程项目中所遇到的非均质土坡的边坡稳定性问题进行了研究，并将结果与中国的相关规范GB 50330—2013《建筑边坡工程技术规范》[9]和玻利维亚当地使用的EM 1110-2-1902Engineering and Design Slope Stability中对边坡的稳定要求进行了对比分析。希望通过此项目问题的研究对后续我国其他外派工程提供相关的参考与借鉴。

2 工程概况

问题边坡地处玻利维亚东北部某两座城市之间，该地区地理条件、气候问题复杂，导致该路段土质分层情况较为严重。经过勘测分析，问题边坡的横断面如图1所示。

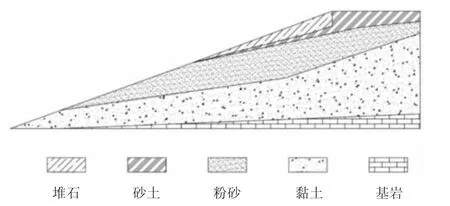
图1 所考虑边坡的横断面形式

本文使用3种方法：Bishop法、Spencer法以及强度折减法，对问题土坡进行了计算分析。考虑到工程设计人员将在施工中对边坡进行人为的改建，且为使结果更具代表性，对问题边坡做了简化，如图2所示，各土层参数如表1所示。

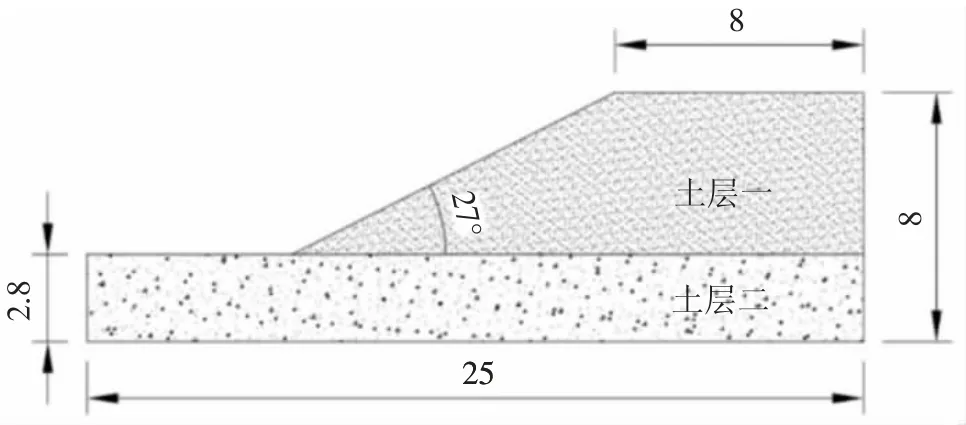
图2 土木计算的几何模型（单位：m）

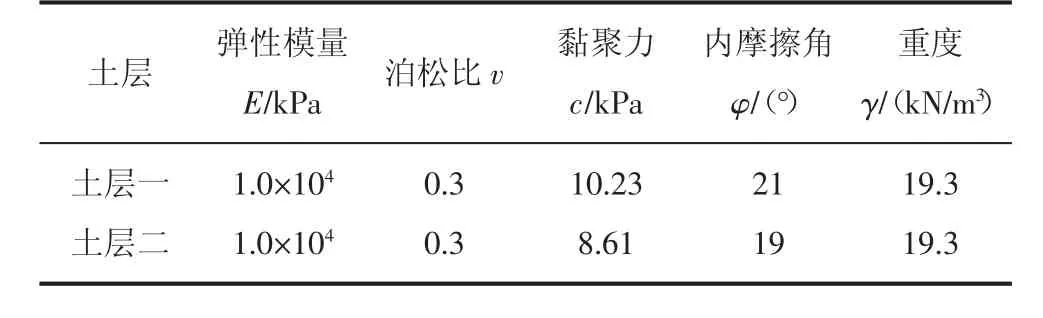
表1 土体参数信息

3 边坡稳定性分析

3.1 Bishop法

Bishop于1955年提出了边坡问题安全系数的广义定义，其表现形式为土体的各滑动面抗剪强度之和与土体实际产生的剪应力之和的商。此方法假定了整个滑动面的边坡平均安全系数与假定的各个土条底部滑动面上的安全系数相等，于是土体的滑裂破坏分析就转变为了平面应变问题，简化了分析过程。虽然该方法不完全满足土体整体平衡条件，但因其适合圆弧滑裂面、迭代计算简单的原因而应用广泛，成了现如今工程师们较为常用的且普遍认可的边坡分析方法。本文边坡算例的Bishop法滑裂面以及相关计算公式如图3所示，由左至右共划分9块土条。

图3 Bishop法土条划分示意图

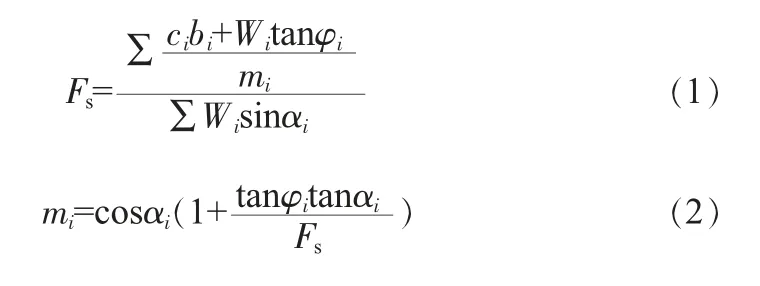
式中，Fs为边坡安全系数；ci为土条的抗剪强度；bi为土条长度；Wi为土条重力；φi为土条内摩擦角；αi为土条底部较水平方向倾角。

结合表1中数据、土条形式以及Bishop法计算公式，得出问题边坡的安全系数为1.956。

3.2 Spencer法

Spencer法于1967年提出，相较于Bishop法具有满足力矩平衡同时满足各向力的平衡、适用滑裂面形状可以是任意而非圆弧的优点。本文边坡算例的Spencer法滑裂面以及计算公式如图4所示，由左至右共划分3块。

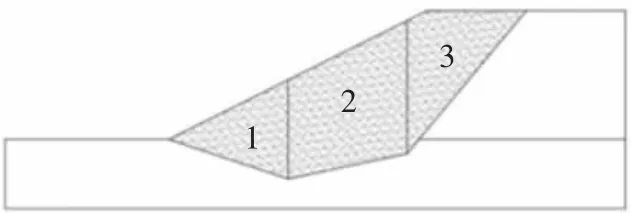
图4 Spencer法土条划分示意图

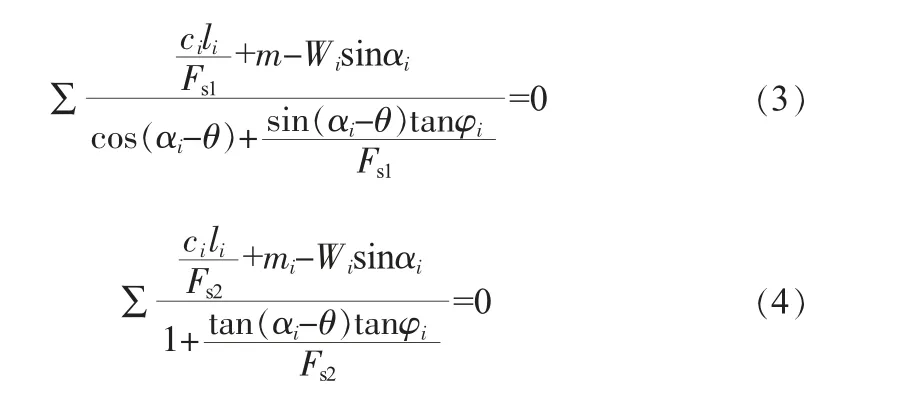
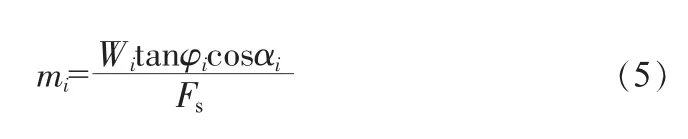
式中，li为土条底部长度；Fs1为满足力平衡方程的边坡安全系数；Fs2为满足力矩平衡方程的边坡安全系数；θ为土条间力的倾角。

通过分别对θ赋值1°，20°，30°，40°并应用编程软件Matlab进行迭代计算，将所得的两对数据组绘制于一张图中，如图5所示，进而得出交点数据，即计算出的边坡安全系数为1.958。

图5 Spencer法计算边坡安全系数

3.3 强度折减法

与传统的极限平衡法相比，有限元法可以考虑更加复杂的工况。本文针对所遇到的问题边坡，采用有限元分析计算软件ABAQUS，对问题边坡进行强度折减分析。同时，考虑到有限元法计算结果对计算模型、材料参数的敏感性以及工程应用的实用性，本文用以下两种方式应对。一是采用三角形一阶单元进行网格划分。这是因为无论是三角形单元还是四边形单元，一阶情况下就能取得较好的计算精度，二阶单元将增加计算的时间成本，不利于工程实用。二是采用以土体“是否形成塑性区贯通”来对边坡是否失稳进行判断。这是因为本文立足于为我国驻外工作人员提供边坡稳定性分析，塑性区贯通判断原理物理意义明确，具有较好的可视化效果，有利于我国外派企业、单位与甲方、监理等更好地进行沟通。

通过计算，问题边坡塑性区贯通的时间为分析步二的Step Time=0.9 397 s时，如图6所示。当塑性区贯通时刻Step Time=1.9 397 s时，对应的边坡安全系数为1.930，如图7所示。

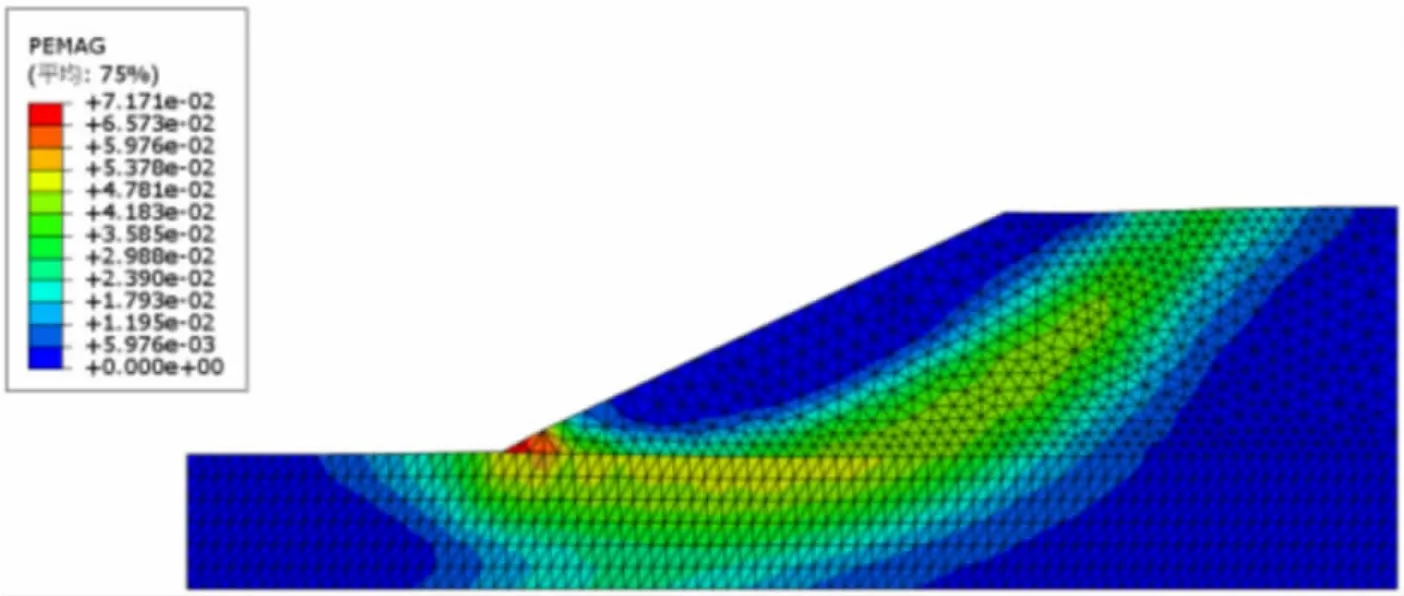
图6 塑性区贯通示意图

图7 采用塑性区贯通判断原理的边坡安全系数

4 依据国内外规范对结果对比分析

目前，我国关于此方面的规范性文件为的GB 50330—2013《建筑边坡工程技术规范》，具体标准为一级永久性边坡在一般工况下安全系数为1.35。本项目中所遇到的问题边坡所采用的标准为EM 1110-2-1902Engineering and Design Slope Stability，它对于永久性边坡的安全系数要求为1.5。将本文采用方法计算出的各安全系数与规范要求汇总整理见表2。

表2 各安全系数汇总

由表2可以得出，无论是工程中广泛应用的极限平衡法还是适用于更复杂工况的有限元法，针对边坡安全系数的计算结果都显著地满足了国内外两者规范的相关要求，证明了这3种方法在边坡稳定分析中具有正确性和有效性，同时也向我国外派工程工作人员证明了，在对边坡稳定性进行分析时，尽管国内外使用不同的规范性条文，工程项目仍可以用上述方法进行分析，且分析结果能满足规范要求的要求。

观察3种分析方法还可得出，传统的极限平衡法分析边坡稳定时结果稍显保守，且其基本假定均将土体视作平面应变问题，忽略了土体之间的动力特性。相比之下，有限元法不仅可以满足静力要求，而且不受边坡几何形状和不均匀材料参数的限制，同时还能提供求解过程中应力、变形的所有信息，这些都是优于极限平衡法的方面。此外，有限元法的计算结果（1.930）与另两种传统极限平衡法（Bishop法：1.956；Spencer法：1.958）的差异最大仅为1.43%，故而依据有限元法求解边坡稳定问题，可以在取得可靠计算结果的同时，提供更多边坡从稳定状态到失稳状态的信息，使得我国驻外工作人员能够更加充分、高效地与当地工作人员进行交流与探讨。

5 结语

使用有限元法分析边坡稳定问题与传统极限平衡法都能取得安全性较高的边坡安全系数，且在本项目案例中都较好地满足了国内外两种边坡稳定性要求，后续我国驻外的相关工作人员可以此为参考进行边坡稳定性分析。

传统的极限平衡法需要进行滑裂面的初拟定，这对于新进入行业，工作经验不是很丰富的工作人员来说有较大考验。相反地，有限元计算方法可以在提供准确、可靠分析结果的基础上，具有更加自动化的优势，一经掌握便可用于批量分析边坡类问题，在我国“一带一路”倡议的推广以及更多国内人员进驻国外工作的当下具有推广意义。