插值粒子滤波在静基座捷联惯导系统初始对准中的应用研究

高 峰

插值粒子滤波在静基座捷联惯导系统初始对准中的应用研究

高 峰

（空军装备部驻西安地区第七军事代表室，西安 710068）

推导了大方位失准角条件下，捷联惯导系统（SINS）静基座初始对准非线性误差模型，提出一种基于插值粒子滤波（DDPF）的SINS静基座初始对准方法。分析了插值非线性滤波原理，结合插值滤波和粒子滤波的特点，利用二阶插值滤波算法得到粒子滤波的重要性密度函数。在静基座状态下分别基于DDF和DDPF滤波算法进行初始对准仿真实验。仿真结果表明，大方位失准角的情况下，DDPF非线性滤波具有更快的收敛速度和更高的对准精度。

非线性滤波；插值粒子滤波；捷联惯导系统；大方位失准角；初始对准

0 引言

初始对准是捷联惯性导航系统（Strap-down Inertial Navigation System，SINS）的一项关键技术，对准精度与对准时间是衡量惯导系统性能指标的重要因素，尤其是对准精度直接影响系统整体的导航性能[1,2]。小失准角条件下，SINS初始对准的误差模型近似为线性，通过标准卡尔曼滤波即可以解决初始对准问题；当失准角较大时，误差模型近似线性化不成立，只能按照非线性模型进行处理[3,4]。

扩展卡尔曼滤波（Extended Kalman Filter，EKF）是应用最为广泛的一种非线性滤波方法[5]，由于略去了二阶以上系统误差项，当系统模型非线性较强时，会给变换后的高斯随机变量的真实验后均值和方差带来较大误差，进而导致滤波精度下降，甚至发散。为了克服EKF算法的不足，2000年Magnus Nogaard等人提出一种插值滤波算法（Divided Difference Filter，DDF），与EKF相比DDF采用Stirling插值公式对非线性模型进行线性化处理，避免了求解微分运算过程，可应用于任意函数，甚至非线性函数不连续且存在奇异点时也能进行状态估计，应用范围广，算法简单，容易实现。此外，DDF在滤波过程中采用了协方差矩阵的平方根形式，保证了协方差矩阵在传播过程的半正定性，具有更好的数值特性，在非线性滤波领域均得到了广泛的关注。但是与EKF算法相同，DDF也是同样基于高斯变量噪声的假设条件[6,7]。粒子滤波（Particle Filter，PF）是一种在完全非线性条件下的贝叶斯估计方法[8]，易于在计算机上实现，并且对系统的动态模型、状态变量的概率分布以及模型阶数均有良好的鲁棒性，不受高斯分布假设条件的限制，受滤波初始误差的影响小，收敛速度快[9,10]。

本文将DDF与PF算法相结合，通过DDF对粒子集进行量测更新生成PF的建议分布，使得从重要性密度函数中取样得到的样本更加逼近真实的后验概率密度，提高粒子滤波的估计精度。并且依据SINS初始对准非线性误差模型，研究了差分粒子滤波器（Divided Difference Particle Filter，DDPF）在SINS大方位失准角初始对准中的应用。

1 大方位失准角下捷联惯导系统误差模型的建立

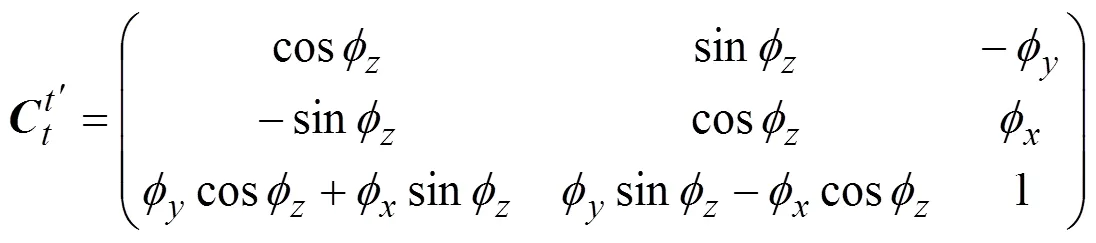
SINS相应的速度和失准角误差模型如式（2）和式（3）所示：

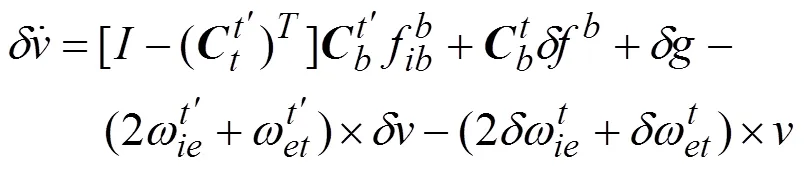
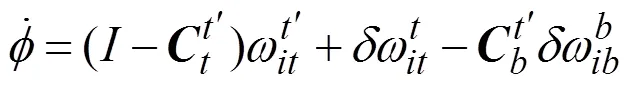
状态向量取：

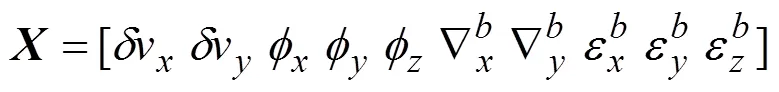
噪声向量取：

取惯导两水平速度误差量为观测量，建立非线性滤波模型如式（5）所示：

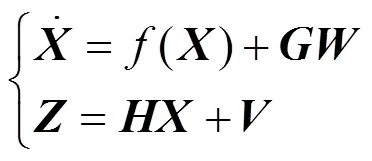
2 插值粒子滤波

2.1 Stirling插值近似

DDF是一种基于Stirling插值近似的非线性滤波方法。根据插值近似的阶数不同，分为一阶插值滤波（1st-DDF）和二阶插值滤波（2nd-DDF），一阶近似与EKF算法精度相当，本文采用2nd-DDF算法。

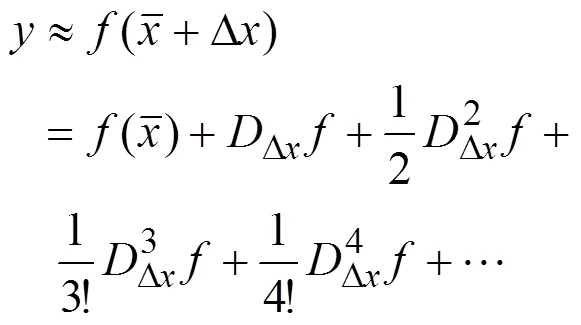
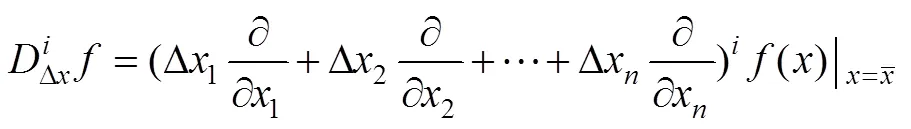
对应的一阶、二阶导如式（8）和式（9）所示：

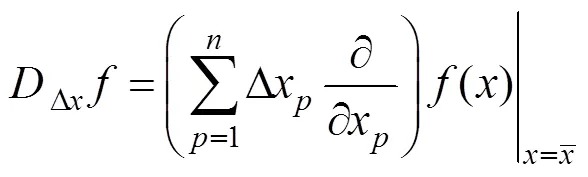
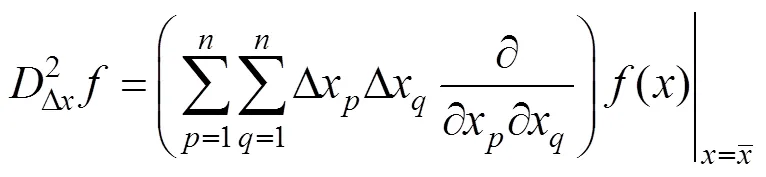
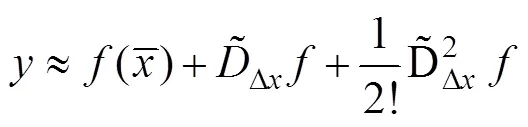
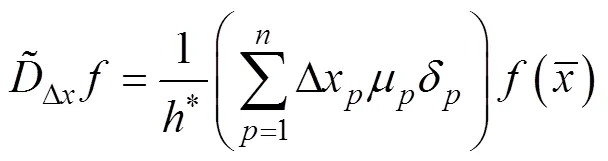
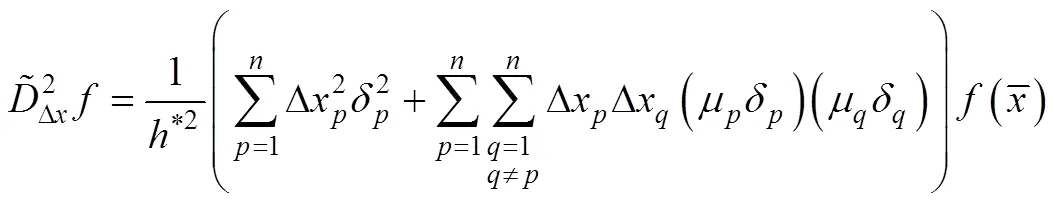
分别表示局部偏差算子和局部平均算子，且分别如式（13）和式（14）所示：

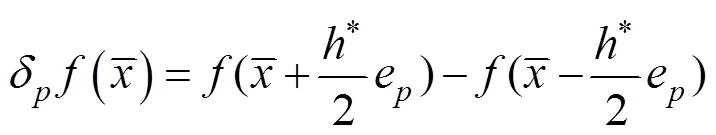
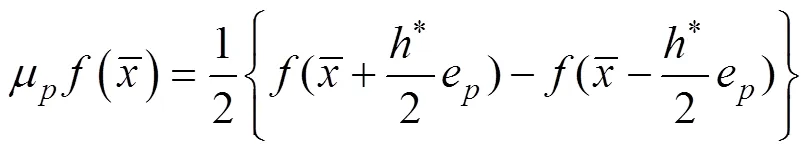
因此式（10）可表示为：

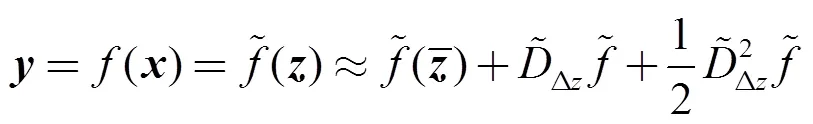
2.2 Stirling插值滤波

考虑如式（16）所示离散状态方程描述的非线性系统：

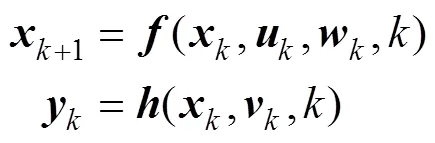
滤波具体步骤如下：

2）采用Cholesky分解法引入四个平方根分解算子如式（19）所示：

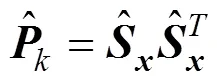
根据如下形式定义的四个差分矩阵如式（20）和式（21）所示：

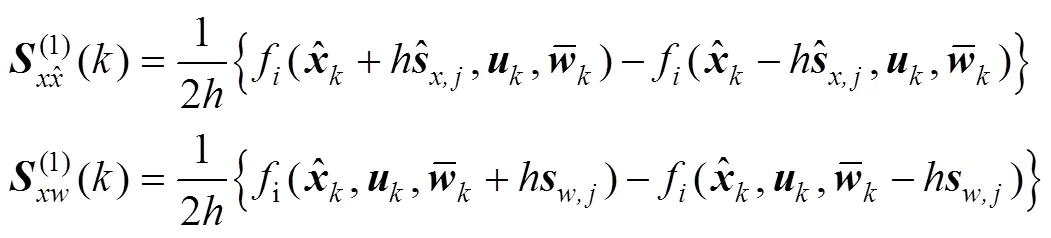
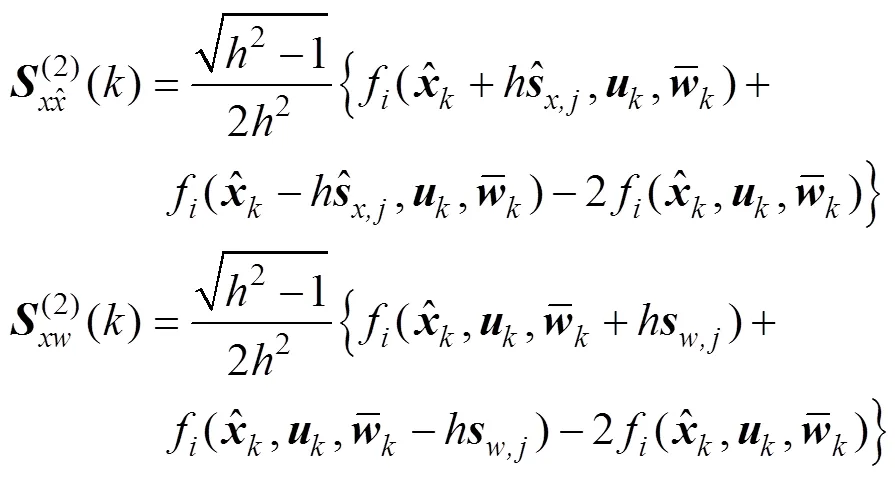
进一步得到相应的状态误差协方差矩阵Cholesky分解因子的时间更新形式如式（22）所示：

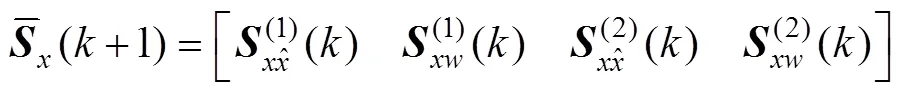
3）状态与协方差时间更新

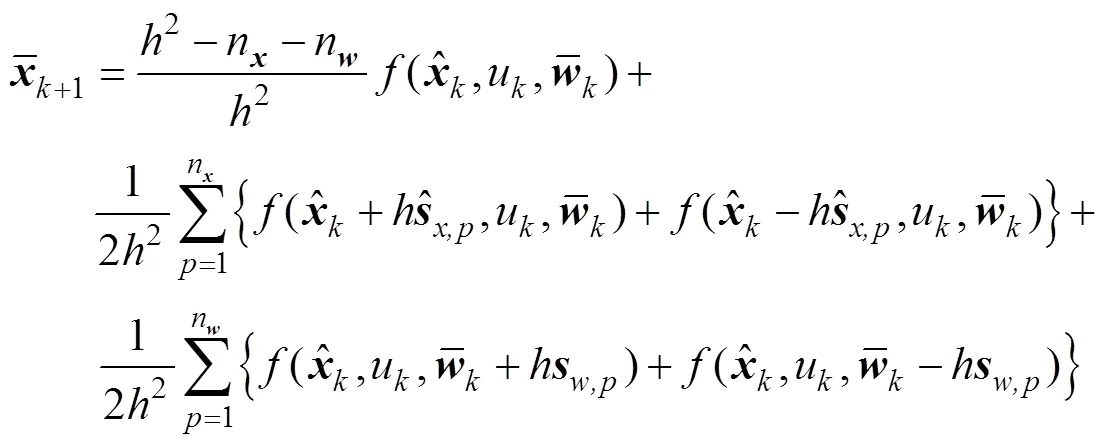
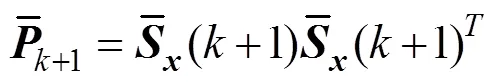
进一步得到式（25）～式（27）：

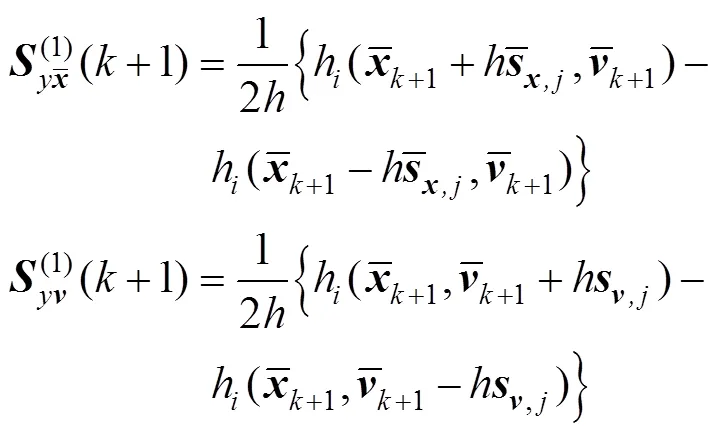
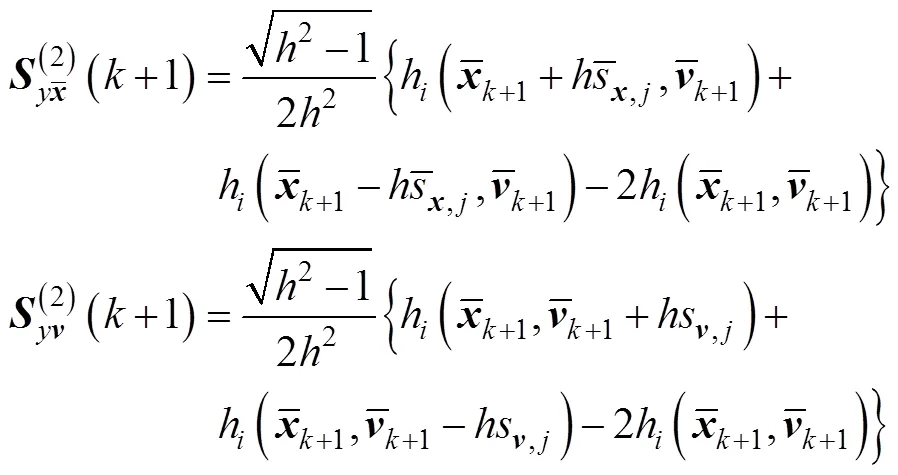
4）计算预测观测向量及其预测协方差矩阵如式（28）所示：

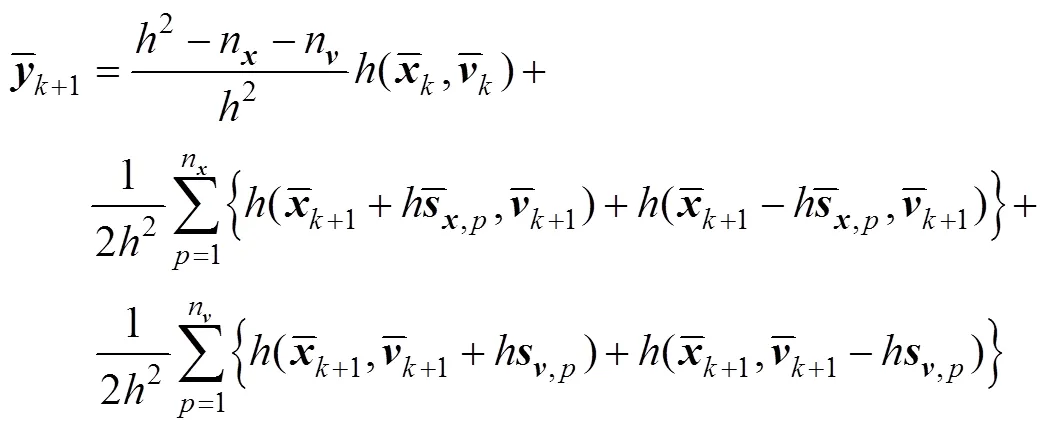
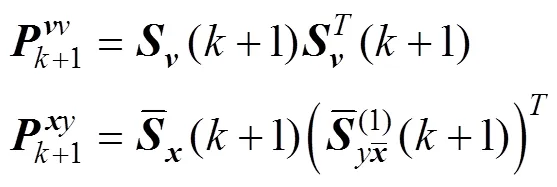
5）量测更新

计算增益矩阵如式（30）所示：

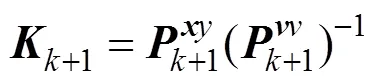
状态向量更新如式（31）所示：

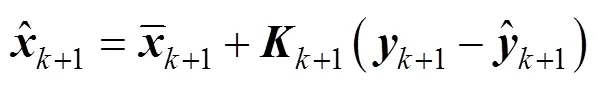
协方差矩阵更新如式（32）所示：

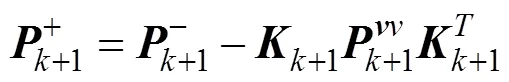
2.3 插值粒子滤波

插值粒子滤波是在粒子滤波框架里利用插值滤波作为重要性密度函数的选取手段，利用当前时刻最新量测数据，产生新的后验概率密度分布，同时通过新的后验概率密度分布重新产生新的粒子，计算粒子的权值并归一化，最后进行重采样完成状态估计。通过结合DDF算法选取重要性密度函数，不仅克服了标准PF难以获得最优重要密度函数分布的缺点，同时整合了最近一次的系统量测数据，能够更好地逼近后验概率密度分布。DDPF算法流程如下：

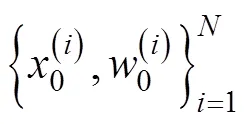
初始权值：

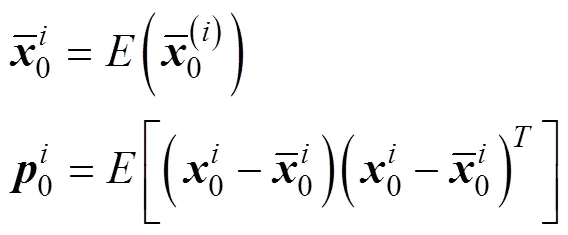
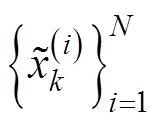
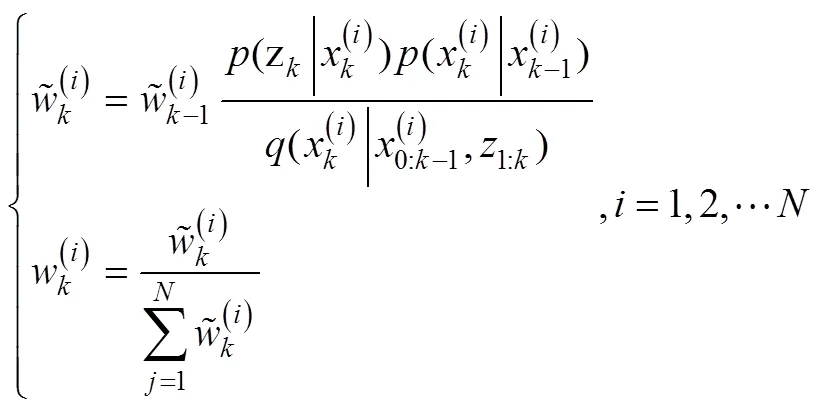
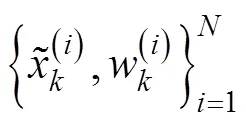
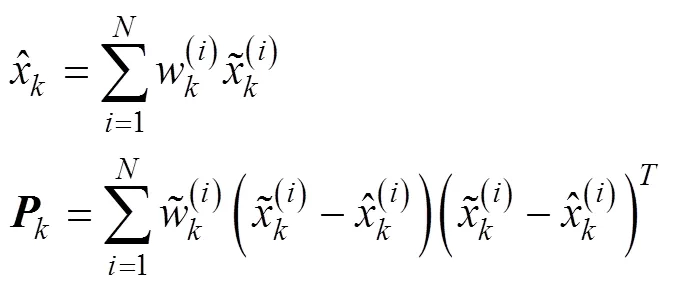
返回第2）步，按新的量测量递推计算下一时刻的状态估计值。

3 仿真验证

3.1 仿真条件

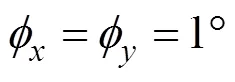
从重要采样函数中采样的粒子数N=100，分别用DDF与DDPF非线性滤波算法进行对准仿真，结果如图1～图3所示，图中实线为DDF对准结果，虚线为DDPF对准结果。

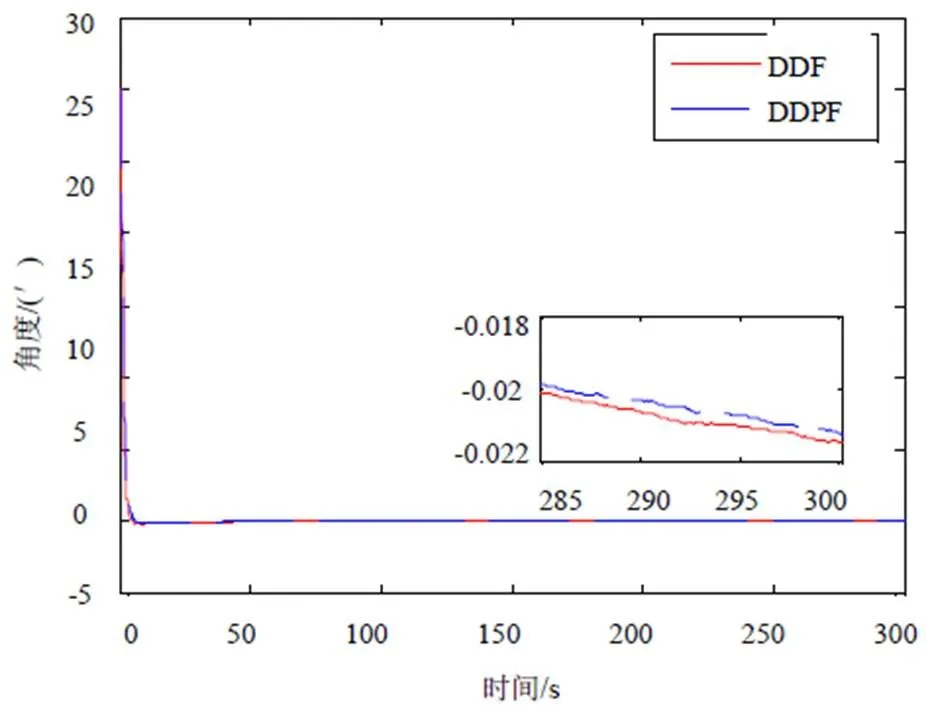
图2 北向失准角估计误差

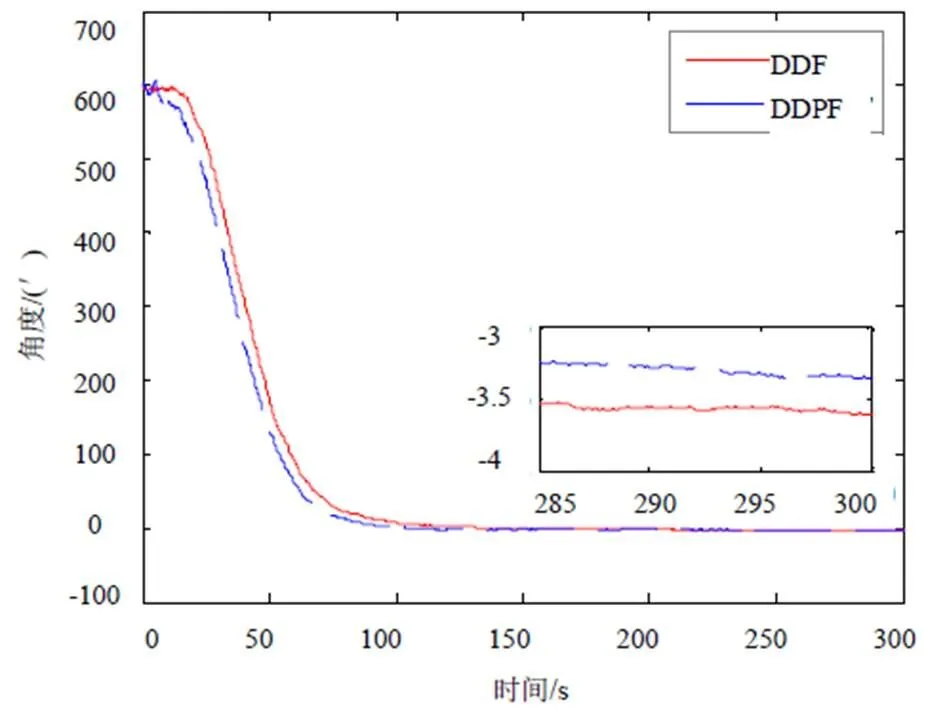
图3 方位失准角估计误差

从图1和图2可以看出，由于水平失准角为小角度，采用DDF与DDPF均能快速收敛到稳态值，DDF估计误差略微高于DDPF，总体来说水平对准精度大体相当，区别不明显。从图3可以看出，在方位失准角对准过程中，DDPF无论在收敛速度还是在估计精度上均优于DDF。在理论对准精度3.24′条件下，DDF算法在300 s时的稳态误差为-3.45′，而采用DDPF算法在300 s时的稳态误差减小到-3.36′。这主要是由于DDPF滤波算法进一步降低了模型线性化误差对系统的影响，增强了鲁棒性。由此比较可以得出，在大方位失准角对准过程中，DDPF具有比DDF更快的收敛速度以及更高的估计精度。

4 结语

对DDPF在捷联惯性导航系统大方位失准角初始对准进行了研究，分析了DDPF算法的数学机理。实验仿真结果表明，DDPF能够很好地适用于大方位失准角初始对准中，比DDF有更高的滤波精度和更快的收敛速度。结果证实了其在大失准角初始对准中的可行性和优越性，为DDPF在静基座惯导系统大方位失准角的初始对准提供了理论依据和计算方法。

[1] 万德钧，房建成. 惯性导航初始对准[M]. 南京：东南大学出版社，1998：9-22.

[2] 秦永元. 惯性导航[M]. 北京：科学出版社，2006.

[3] 杨静，张洪钺，李骥. 预测滤波理论在惯导非线性对准中的应用[J]. 中国惯性技术学报，2003，11（06）：44-52.

[4] 魏春玲，张洪钺，郝曙光. 捷联惯导系统大方位失准角下的非线性对准[J]. 航天控制，2003，21（04）：25-35.

[5] 严恭敏，严卫生，徐德明. 基于欧拉平台误差角的SINS非线性误差模型的研究[J]. 西北工业大学学报，2009，27（04）：511-516.

[6] 王小旭，潘泉，黄鹤，等. 非线性系统确定采样型滤波算法综述[J]. 控制与决策，2012，27（06）：801-812.

[7] M. Nørgaard，N.K. Poulsen，O. Ravn. New Developments in State Estimation for Nonlinear Systems[J]. Automatica，2000，36（11）：1627-1638.

[8] M. Nørgaard，N.K. Poulsen，O. Ravn. Advances in Derivative-Free State Estimation for Nonlinear Systems[D]. Lyngby：Technical University Denmark，2000.

[9] 程向红，李伯龙，王宇. 基于PF的SINS动基座初始对准[J]. 中国惯性技术学报，2009，17（03）：267-271.

[10] 程水英，邹继伟，汤鹏. 免微分非线性Bayesian滤波方法评述[J]. 宇航学报，2009，30（03）：843-857.

Application Research of Interpolated Particle Filter in Initial Alignment of Strap-down Inertial Navigation System in Static

GAO Feng

The nonlinear error model of initial alignment of strap-down inertial navigation system (SINS) under the condition of large azimuth misalignment angle in static is discussed. An initial alignment method based on interpolated particle filter is proposed. The principle of the method is analyzed. Combining the characteristics of interpolated filtering and particle filtering, the importance density function of particle filtering is obtained by using the second-order interpolation filtering algorithm. The simulation results based on DDF and DDPF algorithms show that the DDPF method proposes higher accuracy and faster convergence rate.

Nonlinear Filter; Interpolated Particle Filter; Strap-down Inertial Navigation System; Large Azimuth Misalignment Angle; Initial Alignment

V249.3

A

1674-7976-(2022)-06-396-07

2022-09-08。

高峰（1980.08—），陕西乾县人，硕士研究生，工程师，主要研究方向为导航制导与控制。