高温下地幔矿物质的体积弹性模量及二阶弹性常数

张 玥， 刘 泉

(安徽大学 物理与光电工程学院，安徽 合肥 230601)

体积弹性模量与二阶弹性常数是表征热弹性性质的重要物理量之一，要想全面了解地球内部的成分和热状态，就需要了解所有备选矿物在极端压强和温度条件下的弹性特性.长期以来，人们建立了许多计算固体弹性常数的理论模型，并对其与温度和压强的关系进行了深入的研究[1-4].

2010年，基于弹性常数对温度的假设性依赖关系，Wang等人提出了一种计算有限温度下弹性刚度系数的第一性原理方法，结果表明预测值与已有的实验测量值一致[5].同年，Zen等人使用第一性原理方法研究了Ni，Ti和NiTi合金的结构和弹性性能，其中弹性常数是通过使用密度泛函技术评估能量与小应变的关系来计算的[6].2013年，Ono等人采用从头算分子动力学方法研究了立方体钙钛矿在高压和高温下的弹性，计算结果表明立方体钙钛矿是地球下地幔的一种次要矿物[7]. 2018年，Liu等人利用基于密度泛函微扰理论的第一性原理方法，研究了直至2500 K、100 GPa高温、高压下黄铁矿的等温体积模量、热膨胀系数、热容和熵等热力学性质,与实验结果保持了很好的一致性[8].2019年，Ulian以及Valdrè采用从头算量子力学方法计算了2种矿物的状态方程(EoS)和二阶弹性常数，理论结果与现有文献中实验观察到的一般趋势一致，并进一步扩展了对两相力学性能的认识[9]. 2020年，Argaman与Makov用第一性原理各向异性准调和方法计算了HCP钛的弹性常数，其中包括声子谱作为应变的函数计算，除C13外，弹性常数的温度依赖性与实验结果一致[10]. 2021年，Yang等人采用第一性原理计算，研究Mg，Be，Ti，Zn，Zr和Cd的三阶弹性常数和机械性能，结果与之前的计算和实验值更加吻合[11].

在这里，我们应该指出的是，无论是第一性原理计算还是从头算分子动力学方法[5-11]，其间均包含大量繁杂的计算工作.寻找一种简单直接的方法计算多种矿物质在不同温度下的体积弹性模量及二阶弹性常数，成为当今地球物理学中迫切需要解决的问题.

本文中，我们通过细致分析大量地幔矿物质高温下的热力学参量，基于泰勒级数展开获得热膨胀系数与温度之间的唯象依赖性关系式，并结合热力学公式与Tallon模型[12]，计算了MgAl2O4，Mg2SiO4及Al2O3这3种典型地幔矿物质在不同温度下的体积弹性模量及二阶弹性常数.

1 分析方法

为了探寻体积弹性模量(BT)对温度T的依赖性，Anderson引入了著名的Anderson-Grüneisen参数δT，其定义如下[1]：

(1)

其中：P为压强，α为体积热膨胀系数.方便起见，我们将δT写为δ，将BT写成B.根据α的定义(其中V表示体积)：

(1)式可以写为

(2)

Chopelas 和 Boehler[13]提出了一个等温Anderson-Grüneisen参数δ与体积V之间的线性依赖关系式：

(3)

对给定的晶体，A是一个常数.结合(2)～(3)式并考虑热压项，Kumar得到下列表达式[14-15]：

[1-(δ0+1)α0(T-T0)]，

(4)

式中α0、B0及δ0分别为α、B和δ在初始温度T=T0=300 K时的值.Tallon 已经发现(4)式对于任何一个弹性模量都成立[9]，从而可以用M替代B得到

式中M代表任何一个弹性常数，如C11,C12,C44或者B.从以上分析可知，要求得任意温度下的弹性常数，必须首先求得体积弹性模量与温度之间的关系式.以下分析将帮助我们寻找一种合适的B-T关系式.

通过分析不同温度下大量矿物质的热膨胀系数实验数据，基于泰勒级数展开式，将热膨胀系数与温度之间的依赖性关系表示为

α=α0+α′0(T-T0)+

(5)

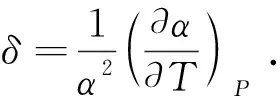
所以(5)式可以改写为

(6)

将(6)式代入(1)式并积分，积分时当温度从T0到T时，相应的体积弹性模量从B0到B.最后得到B与T之间的关系式：

(7)

根据Tallon的推广方法[12]可以将(7)式推广为

(8)

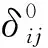
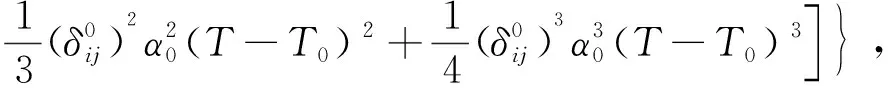
(9)

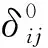
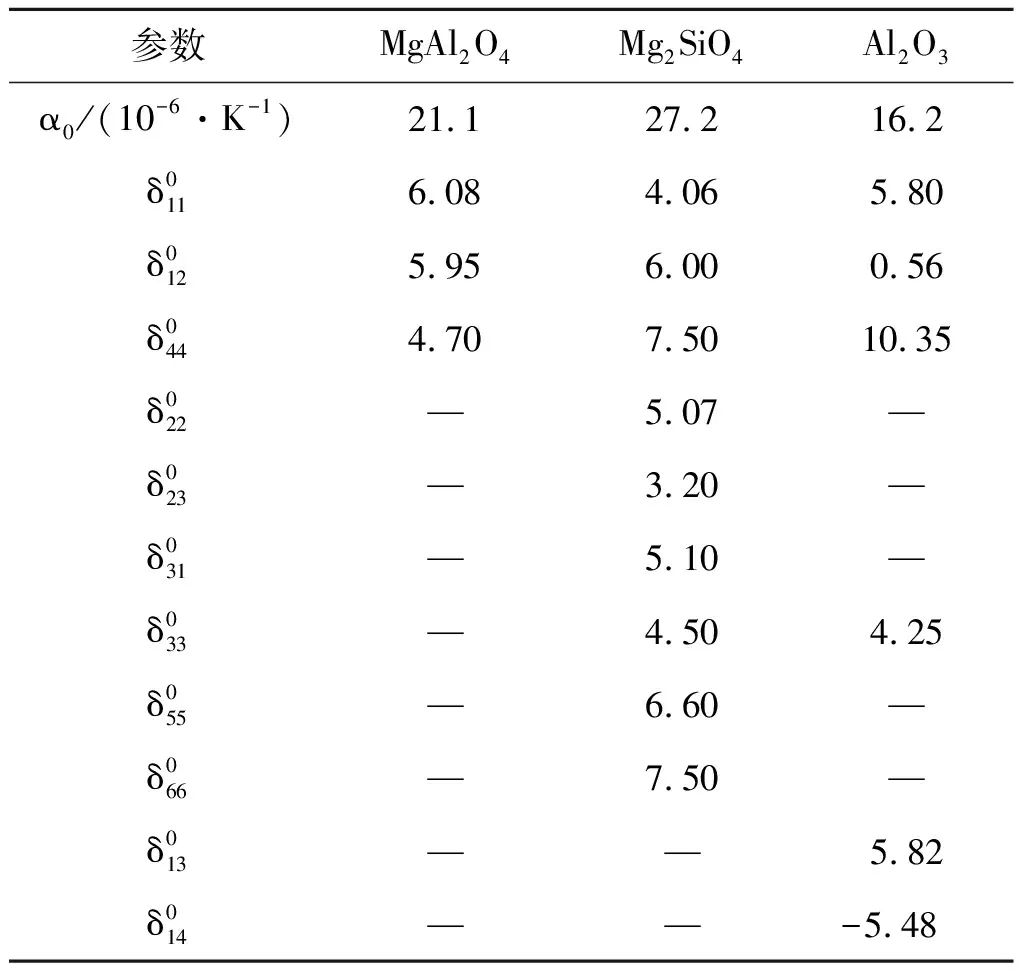
表1 计算所需输入数据(取自文献[1])

2 计算结果和讨论

(5)式已被Kumar[14-15]推广用于计算高温下大量地幔矿物质的弹性常数.在本文中，我们首先运用(5)式和(7)式计算不同温度下NaCl晶体的体积弹性模量.计算结果和实验数据见表2,实验数据取自文献[2]，其中300 K时的Anderson-Grüneisen参数根据文献[2]取作5.95.由表2可知，与实验数据相比，利用(7)式计算的结果误差更小，即(7)式更准确地反映了体积弹性模量随温度的变化规律.

表 2 分别利用 (5)式和 (7) 式计算得到的NaCl体积弹性模量随温度的变化值

对于MgAl2O4，存在3个二阶弹性常数：C11,C12和C44.从图1可以看出，弹性常数计算值与实验值吻合度较高，最大误差仅为0.3%.此外，相对于C12和C44，C11随温度变化的幅度更大.这是因为C11代表纵向弹性，而纵向的应变只引起体积改变而无形状改变，体积的改变又与温度变化密切相关，从而导致了C11的巨大变化.另一方面，C12和C44代表横向弹性即剪切常数，横向应变只引起形状变化而无体积变化，所以C12和C44对温度并不敏感.

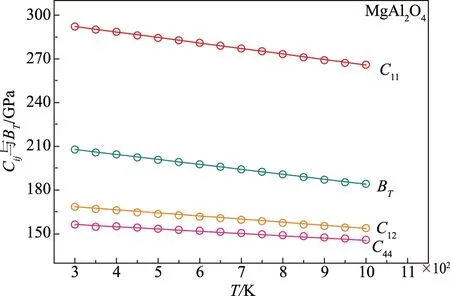
图1 不同温度下MgAl2O4的体积弹性模量(GPa)及二阶弹性常数

(9)式还可用以计算更复杂的矿物质，如Mg2SiO4及Al2O3.对于Mg2SiO4，存在9个二阶弹性常数，而Al2O3存在6个二阶弹性常数.从图2与图3可以看出，根据(7)式与(9)式计算得到的体积弹性模量和二阶弹性常数与实验数值的一般趋势也保持一致.当温度不超过1 000 K时，计算值与实验值完全一致.随着温度的继续升高，少数二阶弹性常数的误差有所增大.Mg2SiO4最大的误差出现在1 700 K时的C33，为3.9%；而Al2O3的最大误差出现在1 800 K时的C33，为3.8%.

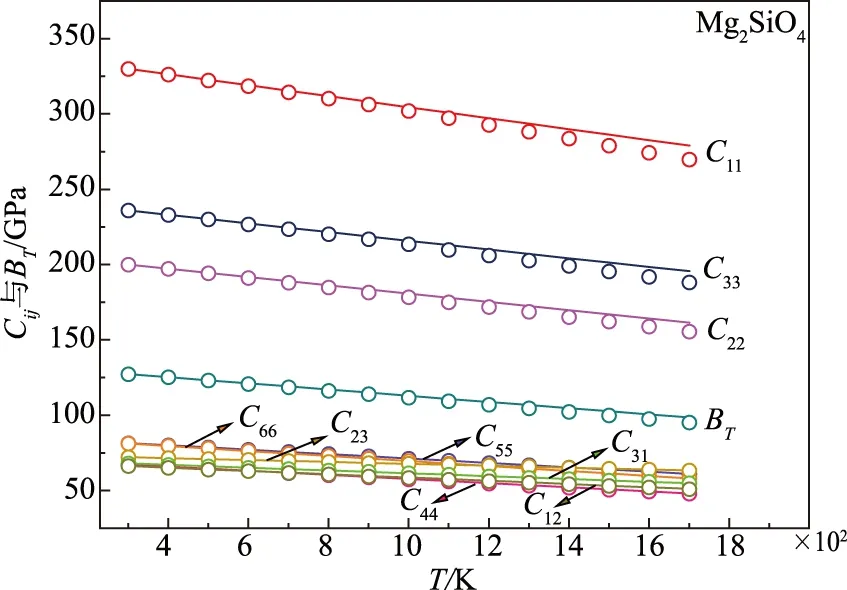
图2 不同温度下Mg2SiO4的体积弹性模量(GPa)及二阶弹性常数

3 结语

本文通过分析大量地幔矿物质高温下的实验数据，结合热力学关系式及高温下矿物质热膨胀系数的唯象公式，提出了一种简单而直接的数值方法以计算不同温度下固体弹性常量.同时，本文所用方法不依赖于矿物质的结构，因此还可应用于更复杂的地幔矿物质.