基于Numerov算法的原子束缚态波数的数值求解

郭志坚， 李小明， 郑兴荣， 孙 乾

(1.陇东学院 电气工程学院，甘肃 庆阳 745000； 2.环县职业中等专业学校，甘肃 庆阳 745000)

随着激光技术的飞速发展，激光与原子分子的相互作用成了热门的研究领域.在强激光与原子分子的相互作用中，电离是最基本的过程[1-2]. 在原子强场电离理论的研究中，计算原子或分子的基态及激发态波函数是一项必要的工作[3-5]. 由于粒子所处的势场通常很复杂，迄今为止能解析求解的势场形式非常少，其相应的波函数很难从理论上通过解薛定谔方程得到，大部分都要通过近似方法或者数值求解得到.近年来，由于计算机技术的快速发展，数值求解微分方程得到了广泛应用，例如，求解一阶微分方程的欧拉法、求解二阶微分方程的龙格库塔法等[5-7].微观粒子满足的薛定谔方程是二阶微分方程，本文利用Numerov算法[8-10]对原子定态薛定谔方程进行求解，采用矩阵解法将哈密顿量简化为三对角矩阵，然后通过矩阵对角化求解本征值及本征函数，不仅大大提升了计算效率，而且求解精度非常高. 另外，引入原子模型势可以对不同原子的波函数进行求解.除氢原子的波函数外，本文还求解了He、Ne、Ar原子的波函数，扩大了其应用范围.

1 电子在库仑场中的运动

在氢原子或类氢原子体系中，电子在原子核的库仑场中运动的势能为

(1)

这时的定态薛定谔方程为

(2)

球坐标系下的拉普拉斯算子为

(3)

定态薛定谔方程的解为

(4)

式中:R(r)为径向波函数，Ylm(θ,φ)为球谐函数，其中l和m分别表示轨道量子数和磁量子数.径向波函数满足下列方程

(5)

解得

(6)

其中:ρ=2Zr/na0,a0是玻尔最小轨道半径，n和l表示主量子数以及轨道量子数.

2 原子波函数的数值求解——Numerov算法

求解氢原子的定态波函数非常方便，但在许多情况下需要求解高激发态的波函数，用解析解处理十分不便.另外，对于多个电子体系(除类氢原子之外)，其势能比较复杂，很难精确求解，数值解法是常用的一种方法. 径向方程(1)可改写为

ER(r).

(7)

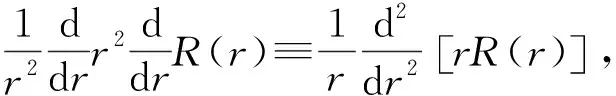
u(r)=rR(r)，

(8)

则(7)式变为

(9)

我们定义一个有效势Vl(r)，则(9)式进一步化简为

(10)

(10)式在形式上与一维定态薛定谔方程相似，只是其中的势能换成了有效势.由于(10)式为一维方程，可改写为

(11)

根据泰勒公式可得

(12)

(13)

(12)式与(13)式相加得

(14)

对于束缚态问题，边界条件为ψn(0)=ψn(X)=0.将最大径向距离X分为N+1份，步长为s，即X=(N+1)s，结合(12)～(14)式得

-ψn(x+s)-ψn(x-s)+2ψn(x)+

(15)

令λn=s2[2mEn/ћ2]，b(x)=2+s2[2mV(x)/ћ2]，则(15)式改写为

-ψn(x+s)-ψn(x-s)+b(x)ψn(x)=λnψn(x).

(16)

将ψn(s),ψn(2s),ψn(3s),…,ψn(is)简写为vn(1)，vn(2)，vn(3)，…,vn(i)，令b(is)=bi，得到下列方程组：

b1·vn(1)+(-1)·vn(2)+

0·vn(3)+0·vn(4)+…=λnvn(1),

(-1)·vn(1)+b2·vn(2)+

(-1)·vn(3)+0·vn(4)+…=λnvn(2),0·vn(1)+(-1)·vn(2)+

(17)

b3·vn(3)+(-1)·vn(4)+…=λnvn(3),

0·vn(1)+0·vn(2)+

(-1)·vn(3)+b4·vn(4)+…=λnvn(4),……

方程组(17)可表示为矩阵形式:

Mvn=λnvn，

(18)

其中

(19)

M为典型的三对角矩阵，通过矩阵对角化可以求出能量本征值λn及相应的本征函数vn.至此，将解一维定态薛定谔方程问题转化为求矩阵的特征值和特征向量问题，从而求解束缚态波函数及能级就非常方便.

3 结果与分析

在具体的数值计算过程中，为使求解方便，统一采用原子单位(atomic units，a.u.).对于能量，1 a.u.=27.2 eV. 为了求解更多原子的束缚态波函数，引入模型势[5]：

(20)

除氢原子外，本文还数值求解了He、Ne、Ar的束缚态波函数，模型势的具体参数见表1.

表1 原子的模型势参数及电离能

4种原子的模型势随径向距离改变的势能曲线见图1.从图1可以看出，由于原子核与核外电子的影响， H、He、Ne、Ar的模型势曲线有明显差异，但随着径向距离增大，当r>5 a.u.时均开始趋于0.

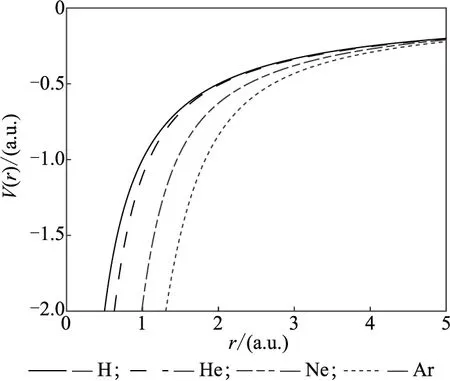
图1 H、He、Ne、Ar的模型势曲线图

3.1 氢原子数值解与解析解

(21)

在数值求解中引入径向波函数u(r)=rR(r)，这4个态径向波函数的数值解和解析解见图2.从图2可以看出，数值解与解析解非常吻合，径向距离在40 a.u.以内完全吻合.这说明数值解的精度很高，采用Numerov算法是可取的.同时程序运行非常快，说明该算法的效率很高.图2中1s态的最大径向距离最小，r=8 a.u.处波函数趋于0，2s、2p态中2s态范围小于2p态，3p态径向距离最大，大约为r=20 a.u.这是因为随着n和l增加，电子具有更大的能量，所以能够运动得更远.

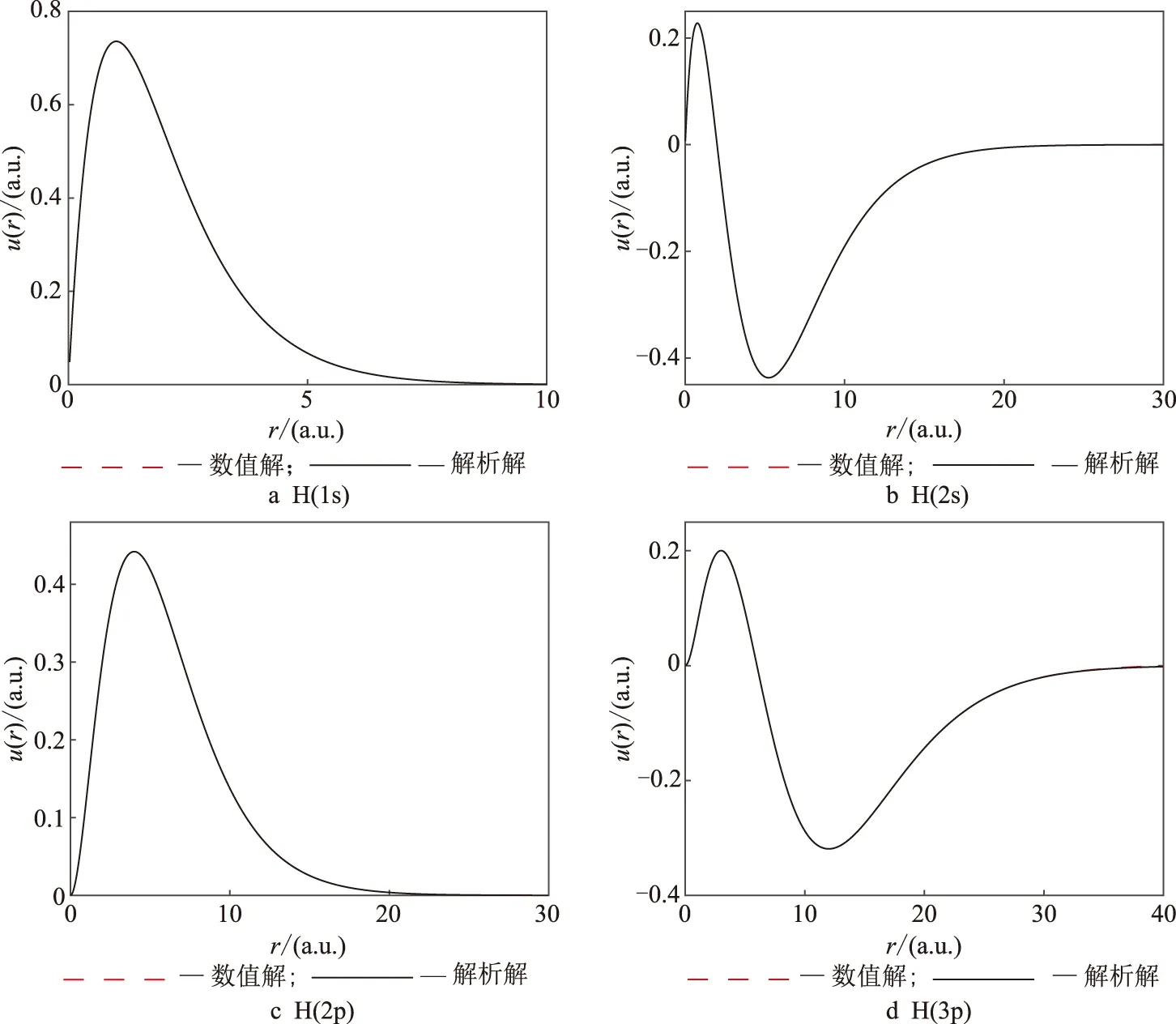
图2 氢原子径向波函数的解析解与数值解

电子在空间径向出现的概率用径向概率密度函数表示.电子在区间[r,r+dr]上出现的概率可表示为

(22)

其中：u2即径向概率密度，u2最大值所对应的r值为原子的最概然半径(量子力学中最概然半径指的是电子在空间中可能出现的最大球壳半径).氢原子1s、2s、3s态及2p、3p和 4p态的径向概率密度函数的数值计算结果见图3，其中每条曲线的最大峰值对应的r为原子的最概然半径.从图3可以看出波函数径向概率分布的节点数满足nr=n-l-1(不包括边界点)，即1s、2s、3s态的节点数分别为0、1、2，而2p、3p 、4p态的节点数也分别为0、1、2.

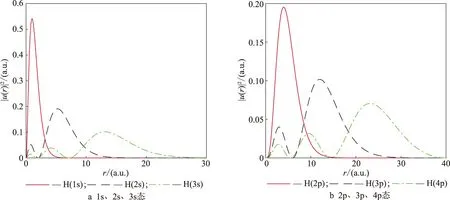
图3 氢原子径向概率分布的数值解

3.2 He、Ne、Ar原子的波函数

利用模型势给出了He原子1s态和2p态的径向波函数(图4).显然，2p态比1s态的径向距离大.

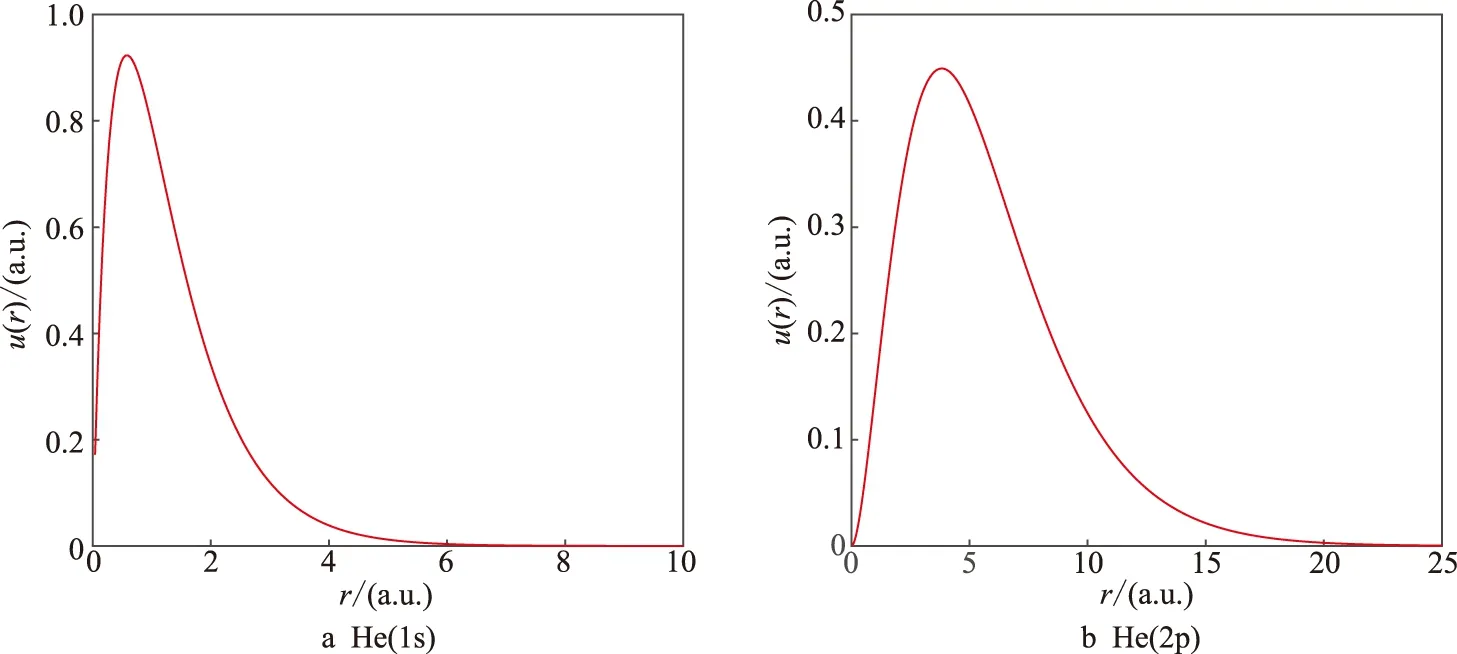
图4 氦原子径向波函数的数值解

图5为Ne原子的3s态和2p态波函数，其中基态为2p态，径向波函数节点数为0，而3s态节点数为2. 图6为Ar原子的3p态和4s态波函数，3p态为基态，4s态为第一激发态，其中3p态节点数为1，4s态节点数为3. 根据量子理论，节点处电子出现的概率为0，即电子在该处不出现.

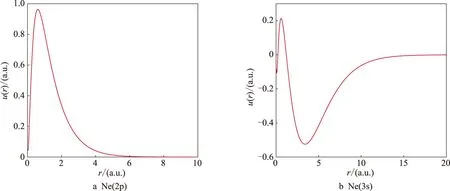
图5 氖原子径向波函数的数值解

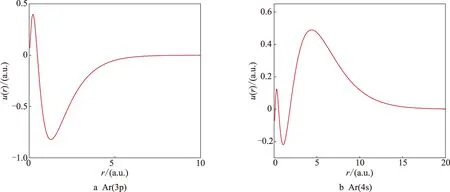
图6 氩原子径向波函数的数值解

将氢原子、氦原子、氖原子及氩原子的基态波函数H(1s)、He(1s)、Ne(2p)与Ar(3p)作比较，结果见图7. 从图7可以明显地发现Ne与He的基态波函数非常相似，其趋于0的形式也保持一致；而H与Ar的基态波函数在r=1 a.u.处相交，此后其形式较为接近，在r>1 a.u.的区域，由于Ar原子基态波函数存在节点，从而有了区别，但总体而言，H与Ar的基态波函数具有较高的相似性.由表1可知, H与Ar的电离能分别为0.5 a.u.和0.579 a.u.,十分接近; 而Ne与He的电离能分别为0.793 a.u.和0.904 a.u.，也比较接近. 这说明原子的基态波函数与原子电离能的相关性很高.

图7 H、He、Ne、Ar的基态波函数

4 结论

本文详细介绍了氢原子束缚态径向波函数的解析求解过程，在此基础上引入Numerov算法将氢原子束缚态波函数的求解数值化，借助于FORTRAN和MATLAB软件可以轻松求解氢原子的束缚态波函数.本文将氢原子的束缚态波函数(1s、2s、2p、3p)的数值解与解析解作了对比，结果非常吻合.除此之外，我们引入了模型势，可以对不同的原子束缚态进行求解.本文给出了He、Ne、Ar原子的模型势参数及电离能，数值求解了He、Ne、Ar原子的部分束缚态波函数.最后，对比了H、He、Ne、Ar原子的基态波函数，发现H与Ar基态波函数较为相似，He与Ne基态波函数较为接近，结果表明原子基态波函数与电离能有直接关系.